基于優化遺傳算法城市立體車庫信號調度算法的研究＊

張書茂

（安徽城市管理職業學院，安徽合肥 230000）

0.引言

近年來，經濟的高速發展，生活質量的不斷提高，除了公用車輛的數量相對穩定，私家車數量上迅速增長，立體車庫應運而生，目前大都是地下城市立體車庫，同普通停車場主要區別是層數的增加，有一部分立體車庫，已經安裝有升降裝置的，在空間上得到了一定的優化利用，但是相當一部分還是依據信號的順序對升降裝置即堆垛機的調度控制，即單體控制[1]，那么對堆垛機的調度優化方面還需要進一步的研究，提出了一種基于遺傳算法堆垛機的路徑優化算法[2]，為立體車庫的堆垛機路徑優化提供參考。

1.遺傳算法

1.1 相關概念

1975 年J.Holland 教授提出遺傳算法簡稱GA。其主要思想是通過多次迭代方式在實際問題空間里，求解達到一定程度的最優解。

1.2 常用操作

在遺傳算法迭代的過程中，因為只考慮內部信息，適應度函數對迭代的次數和運行時間起著決定性作用。適應度函數g(x)主要有：（1）目標函數為參數；（2）估算參數Dmax|min為參數；（3）通過界限值D 參數（保守估計）。

實際運行中，會產生兩種極端的現象：

第一種：差異比較大特殊的個體，對優化選擇的趨勢影響到全局。第二種：差異比較小的個體，對優化效率有一定的影響。為了減少以上個體的數量，對適應度函數g(x)要滿足如下要求：

圖1 遺傳算法流程圖

(1)g(x)函數要連續性，正值區間，具體值。

(2)g(x)在保證目標函數的條件下，簡單線性化。

(3)g(x)的參數在達到目標函數要求范圍內，通用化。

1.3 算法流程（圖1）

2.遺傳算法的改進

2.1 相關思路

在遺傳算法求解最短路徑的問題上，除了適應度g(x)函數有很重要的特點外，在初始化種群中求解的空間范圍中的個體也很重要，通常是隨機選取后進行迭代運算[3]，那么在求解空間的選擇或者樣本空間的選擇也很重要，不同的樣本空間的選擇，得到的結果也是不同的，為了保證在樣本空間具有一定的連續性相關性，提高遺傳算法的運行時間和空間的效率，引入蟻群算法(Ant Colony algorithm)，對求解空間的樣本進行優化，提升遺傳算法。

蟻群算法是通過蟻群尋找食物的整個過程的思想，即個體之間交流信息找到最佳路徑。

2.2 相關概念

假設立體車庫有n 個停車位，先求解樣本空間然后求解最佳路徑。其中n 個停車位表示為n 個節點，dij代表第i 和第j 個節點的距離，其中i，j ∈n。

n個停車位對應n個螞蟻，作為各個螞蟻的位置的初始化。

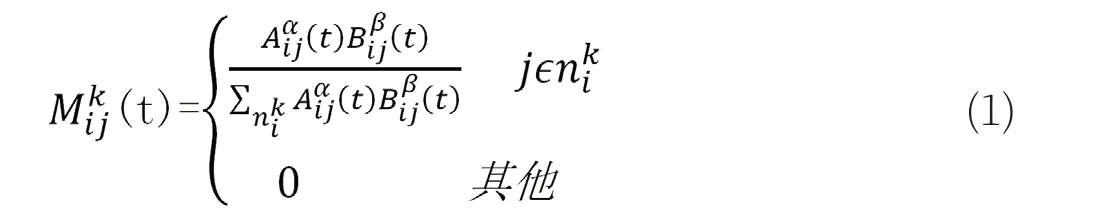
相關說明: Aijα(t)表示節點i 與節點j，t 時刻路徑上的剩余信息。 Bijβ(t)表示節點i 與節點j 的概率值，通常用1/dij表示，其中的α 和β 是用來調節的參數，該公式表明：選中的概率與該節點的信息量成正比，與距離成反比。

每個螞蟻k 都有一個線性表結構L 與之對應，用來記錄所訪問過的節點。其中用ρ 表示L 的內容更替的程度[4]。

所有節點完成一次遍歷后，每個節點的信息調整如下：

2.3 改進方法

步驟1：n 個螞蟻對應n 個停車位。

（3）循環結束條件進行判斷，滿足跳出循環，反之繼續循環。

步驟4：通過步驟3 的結果然后進行遺傳算法的求解。

2.4 相關說明

通過分析，α=1，β=5，ρ=0.5 比較穩定，C,Q 基本沒有影響，一般取值為C=10，Q=100。特別說明一點：一般循環體選用次數或者兩次遺傳運算結果的差異值[6]（差異值允許的一定范圍）。

3.數據分析

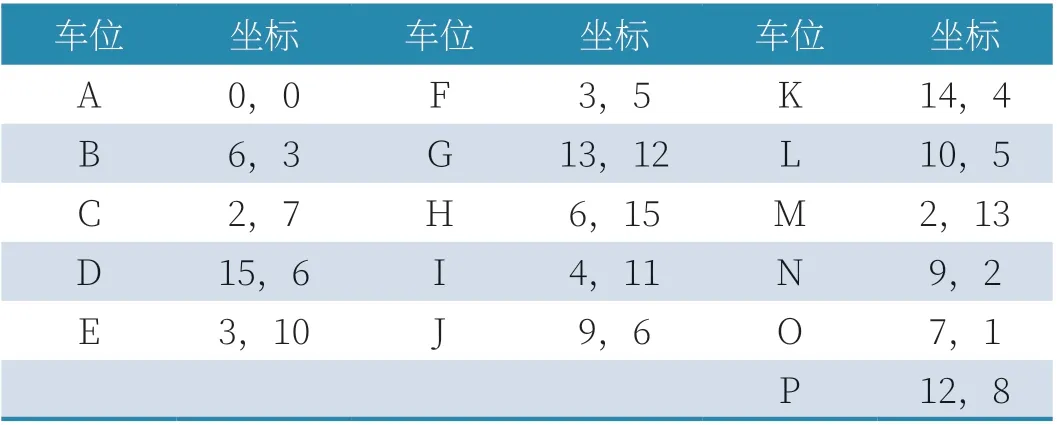
表1 空停車位表

假設在某一個立體車庫的某層車庫，每個停車位之間長度為1m，寬度也為1m，堆垛機的運行速度勻速為1m/s,本仿真實驗不考慮時間進行測試，本車庫總共停車位為225 個，其中209 已經停滿，還有16 個車位為空位，空車位的坐標，如表1 所示。

（2）通過傳統的遺傳算法得的路徑為：A-C-J-F-B-IE-M-H-P-D-G-L-K-O-N-A,對應的路徑長度為：9+8+7+5+10+2+4+6+13+5+8+10+5+10+3+11=116，因為傳統的遺傳算法求得結果不一定是最優的結果，是相對優解（允許在一定的范圍）。

（3）通過蟻群算法優化初始種群，再進行遺傳算法求解最短路徑:A-F-B-E-I-M-H-G-P-J-L-N-O-B-K-D-A,對應的路徑長度：8+5+10+2+4+6+10+5+5+2+4+3+3+9+3+21=100。

可以得到傳統遺傳算法得到解是相對優解，通過蟻群算法初始化種群后在進行遺傳運算得到的解更好一些。

通過算法得分析可以得到，通過蟻群算法初始化種群后，遺傳算法得運算空間的基本解決，在通過適應度函數進行微調就基本達到相對的優解。

4.結語

本文探討了立體車庫信號調度堆垛機的最短路徑的問題，討論的案例是在平面二維車庫進行的，適應度的平方差比較小，邊緣的適應度高的節點以及客戶停車時間的參數對路徑的選擇的影響有待進一步的研究。