蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析

陶小會(huì)，李國(guó)龍，徐 凱，李傳珍

（重慶大學(xué)機(jī)械傳動(dòng)國(guó)家重點(diǎn)實(shí)驗(yàn)室，重慶400044）

隨著制造業(yè)的快速發(fā)展，對(duì)數(shù)控機(jī)床加工精度的要求越來(lái)越高。影響數(shù)控機(jī)床加工精度的因素包括幾何誤差、熱誤差、力誤差和伺服誤差等，其中幾何誤差所占比例較高。提高數(shù)控機(jī)床加工精度的方法有精度設(shè)計(jì)和誤差補(bǔ)償［1］，但蝸桿砂輪磨齒機(jī)等機(jī)床的結(jié)構(gòu)復(fù)雜，誤差種類多，盲目進(jìn)行精度設(shè)計(jì)和誤差補(bǔ)償?shù)某杀靖摺⑿实颓译y以取得較好的效果。因此，通過(guò)建立機(jī)床幾何誤差模型，識(shí)別影響機(jī)床空間精度的關(guān)鍵幾何誤差項(xiàng)，對(duì)機(jī)床精度設(shè)計(jì)和誤差補(bǔ)償有理論指導(dǎo)意義。

常用的機(jī)床幾何誤差建模理論包括多體系統(tǒng)理論［2-4］、剛體運(yùn)動(dòng)學(xué)理論［5］和齊次坐標(biāo)變換理論［6-8］等，但基于上述理論的幾何誤差建模過(guò)程較復(fù)雜，需要在每個(gè)運(yùn)動(dòng)軸上建立局部坐標(biāo)系。旋量理論［9-10］可以在全局坐標(biāo)系下描述剛體運(yùn)動(dòng)，簡(jiǎn)化了建模過(guò)程，被廣泛應(yīng)用于機(jī)器人領(lǐng)域，但較少用于機(jī)床運(yùn)動(dòng)學(xué)建模。對(duì)于幾何誤差的敏感度分析，國(guó)內(nèi)外許多學(xué)者進(jìn)行了研究，例如：黃強(qiáng)等［11］對(duì)影響滾齒機(jī)加工精度的關(guān)鍵誤差源進(jìn)行了識(shí)別；程強(qiáng)等［12］利用矩陣微分法識(shí)別出機(jī)床的關(guān)鍵幾何誤差；Chen等［13］利用矩陣微分法對(duì)五軸數(shù)控機(jī)床的37個(gè)幾何誤差進(jìn)行了敏感度分析；Cheng等［14］基于Sobol法識(shí)別了立式加工中心的關(guān)鍵幾何誤差；Zou 等［15］采用基于方差的敏感度分析方法，研究了三軸金剛石車床中每個(gè)誤差源對(duì)加工誤差的影響；廖琳［16］利用敏感度分析理論分析了影響機(jī)床姿態(tài)誤差的主要幾何誤差；Guo等［17］通過(guò)擴(kuò)展傅里葉振幅敏感度測(cè)試（extended Fourier amplitude sensitivity test，EFAST）法確定了每個(gè)幾何誤差對(duì)機(jī)床空間精度的影響；Cheng等［18］提出了一種基于指數(shù)螺旋理論和Morris 法的誤差敏感度分析方法，并將它用于機(jī)床加工精度全局敏感度分析；夏長(zhǎng)久等［19］建立了幾何誤差-齒面誤差模型，并基于Morris法識(shí)別了影響磨齒機(jī)精度的關(guān)鍵幾何誤差。綜上所述，目前幾何誤差敏感度研究主要針對(duì)通用機(jī)床，而較少關(guān)注蝸桿砂輪磨齒機(jī)。

為此，筆者提出一種基于旋量理論和Sobol法的蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析方法。首先，基于旋量理論建立蝸桿砂輪磨齒機(jī)幾何誤差模型；然后，采用Sobol法對(duì)蝸桿砂輪磨齒機(jī)磨削過(guò)程進(jìn)行幾何誤差敏感度分析；最后，修正蝸桿砂輪齒磨機(jī)的關(guān)鍵幾何誤差項(xiàng)，通過(guò)仿真分析對(duì)比修正前后機(jī)床的空間誤差分量和3種測(cè)量模式下球桿儀的桿長(zhǎng)，以驗(yàn)證敏感度分析結(jié)果的正確性和有效性。

1 蝸桿砂輪磨齒機(jī)幾何誤差建模

1.1 旋量理論

根據(jù)Chasles定理，任意剛體的運(yùn)動(dòng)都可以通過(guò)繞某一軸的轉(zhuǎn)動(dòng)加上沿該軸的移動(dòng)來(lái)實(shí)現(xiàn)，該組合運(yùn)動(dòng)稱為旋量運(yùn)動(dòng)。假設(shè)運(yùn)動(dòng)旋量，其中為旋轉(zhuǎn)方向的單位向量為移動(dòng)方向的單位向量，運(yùn)動(dòng)位移為θ，則剛體運(yùn)動(dòng)變換矩陣可以用運(yùn)動(dòng)旋量的指數(shù)表示：

式中：

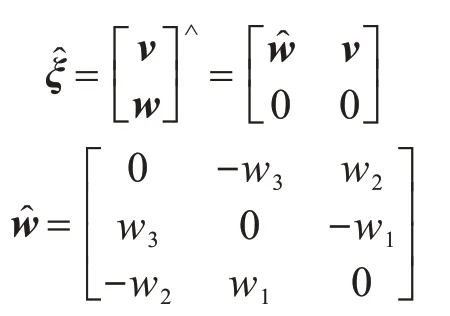
對(duì)于平動(dòng)軸，當(dāng)w = 0時(shí)，有：

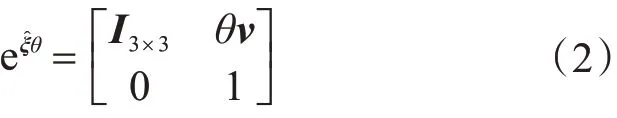
對(duì)于旋轉(zhuǎn)軸，當(dāng)w ≠0時(shí)，有：

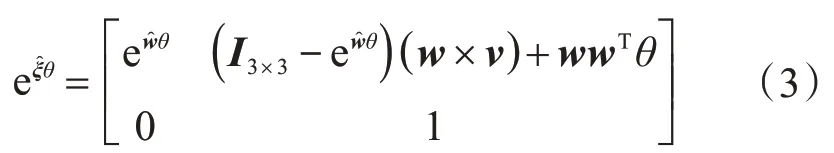
運(yùn)動(dòng)鏈中的剛體經(jīng)過(guò)一定轉(zhuǎn)動(dòng)和移動(dòng)之后，第n個(gè)剛體相對(duì)于基座標(biāo)系的運(yùn)動(dòng)變換矩陣可表示為：

式中：gbn(0)為初始位置時(shí)第n 個(gè)剛體相對(duì)于基座標(biāo)系 的 運(yùn) 動(dòng) 變 換 矩 陣；ξi(i = 1，2，…，n) 和θi(i =1，2，…，n)分別表示第i 個(gè)剛體的運(yùn)動(dòng)旋量和運(yùn)動(dòng)位移。

1.2 蝸桿砂輪磨齒機(jī)幾何誤差分析

YW7232 型蝸桿砂輪磨齒機(jī)如圖1 所示。由于制造缺陷和裝配誤差，蝸桿砂輪磨齒機(jī)工作時(shí)會(huì)產(chǎn)生幾何誤差，這些幾何誤差可分為位置相關(guān)幾何誤差和位置無(wú)關(guān)幾何誤差。蝸桿砂輪磨齒機(jī)有3個(gè)直線軸（X 軸、Y 軸、Z 軸）和3 個(gè)旋轉(zhuǎn)軸（A 軸、B 軸、C 軸），其中：B軸為電主軸，精度高，可忽略其幾何誤差；其余每軸運(yùn)動(dòng)時(shí)均會(huì)產(chǎn)生6 項(xiàng)位置相關(guān)幾何誤差。以X軸為例，X 軸運(yùn)動(dòng)時(shí)會(huì)產(chǎn)生沿X 方向的定位誤差δx(x)，滾轉(zhuǎn)誤差εx(x)，沿Y、Z 方向的直線度誤差δy(x)、δz(x)，俯仰誤差εy(x) 以及偏轉(zhuǎn)誤差εz(x)。同時(shí)，蝸桿砂輪磨齒機(jī)還存在11項(xiàng)位置無(wú)關(guān)幾何誤差，包括直線軸間的3項(xiàng)垂直度誤差（φzy、φxy、φxz）以及旋轉(zhuǎn)軸的8項(xiàng)安裝誤差（δya、δza、φya、φza、δxc、δyc、φxc、φyc）。綜上，蝸桿砂輪磨齒機(jī)共有41項(xiàng)幾何誤差，具體誤差項(xiàng)及對(duì)應(yīng)編號(hào)如表1所示。

1.3 基于旋量理論的幾何誤差建模

蝸桿砂輪磨齒機(jī)的拓?fù)浣Y(jié)構(gòu)如圖2所示，主要由2 個(gè)分支組成：刀具分支和工件分支。其中，刀具分支由機(jī)床床身、X軸、Z軸、A軸、Y軸、B軸和刀具組成；工件分支由機(jī)床床身、C軸和工件組成。

蝸桿砂輪磨齒機(jī)有3個(gè)移動(dòng)軸和3個(gè)旋轉(zhuǎn)軸，理想情況下，機(jī)床的旋量運(yùn)動(dòng)為沿X軸移動(dòng)x、沿Y軸移動(dòng)y、沿Z 軸移動(dòng)z、繞A 軸轉(zhuǎn)動(dòng)角度a、繞B 軸轉(zhuǎn)動(dòng)角度b、繞C軸轉(zhuǎn)動(dòng)角度c。以A軸為例分析誤差運(yùn)動(dòng)旋量，A軸的位置無(wú)關(guān)幾何誤差運(yùn)動(dòng)可以用2組旋量運(yùn)動(dòng)表示：沿Y軸移動(dòng)δya，繞Y軸轉(zhuǎn)動(dòng)角度φya，記為ξeya；沿Z 軸移動(dòng)δza，繞Z 軸轉(zhuǎn)動(dòng)角度φza，記為ξeza。A 軸的位置相關(guān)幾何誤差運(yùn)動(dòng)可以用3組旋量運(yùn)動(dòng)表示：沿X 軸移動(dòng)δx(a)，繞X 軸轉(zhuǎn)動(dòng)角度εx(a)，記為ξex(a)；沿Y軸移動(dòng)δy(a)，繞Y 軸轉(zhuǎn)動(dòng)角度εy(a)，記為ξey(a)；沿Z 軸移動(dòng)δz(a)，繞Z軸轉(zhuǎn)動(dòng)角度εz(a)，記為ξez(a)。蝸桿砂輪磨齒機(jī)各軸的理想運(yùn)動(dòng)旋量ξij和誤差運(yùn)動(dòng)旋量ξej如表2所示，其中j = x，y，z，a，b，c。

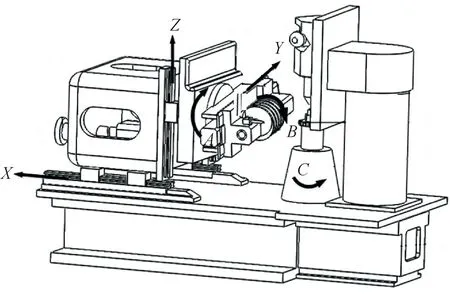
圖1 YW7232型蝸桿砂輪磨齒機(jī)示意圖Fig. 1 Schematic diagram of YW7232 worm wheel gear grinding machine

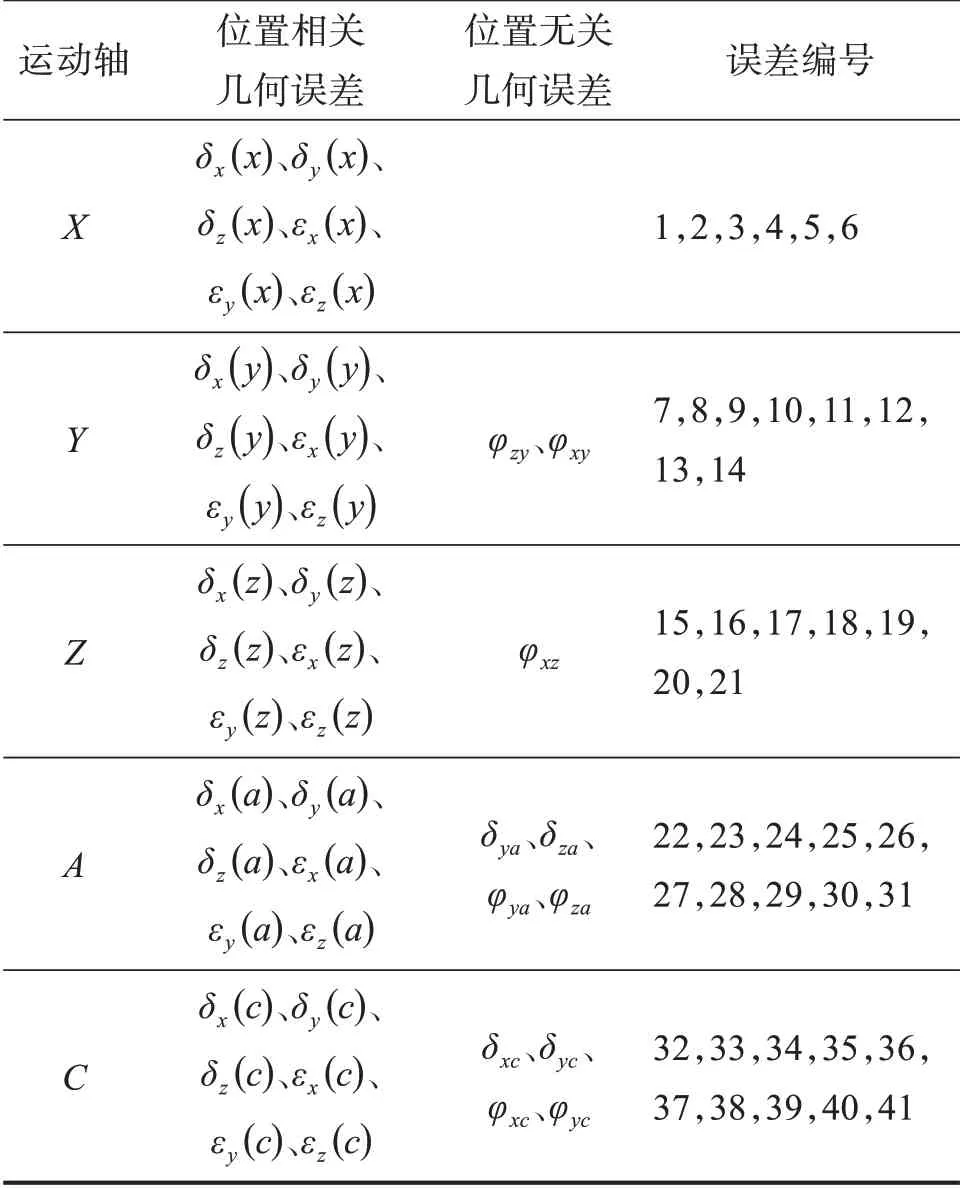
表1 蝸桿砂輪磨齒機(jī)幾何誤差及對(duì)應(yīng)編號(hào)Table 1 Geometric errors and corresponding numbers of worm wheel gear grinding machine

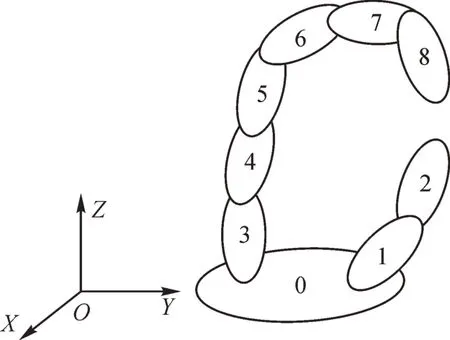
圖2 蝸桿砂輪磨齒機(jī)拓?fù)浣Y(jié)構(gòu)Fig. 2 Topology structure of worm wheel gear grinding machine

由旋量理論可知，工件相對(duì)于機(jī)床的運(yùn)動(dòng)變換矩陣可表示為：

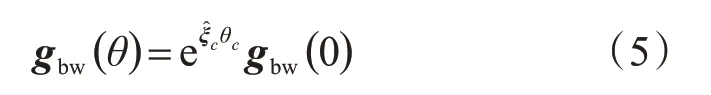
刀具相對(duì)于機(jī)床的運(yùn)動(dòng)變換矩陣可表示為：

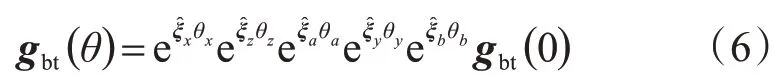
則刀具相對(duì)于工件的運(yùn)動(dòng)變換矩陣為：

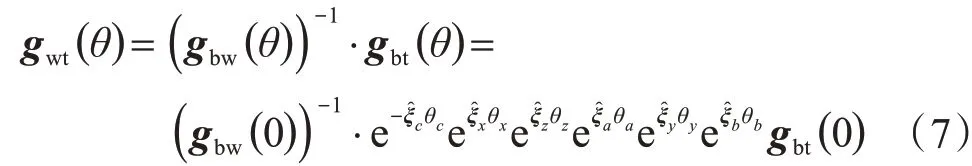
理想情況下，刀具相對(duì)于工件的運(yùn)動(dòng)變換矩陣為：

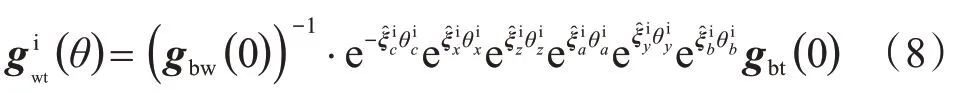
式中：θji表示理想情況下j軸的運(yùn)動(dòng)位移表示理想情況下j軸的運(yùn)動(dòng)變換矩陣。

實(shí)際情況下，刀具相對(duì)于工件的運(yùn)動(dòng)變換矩陣為：

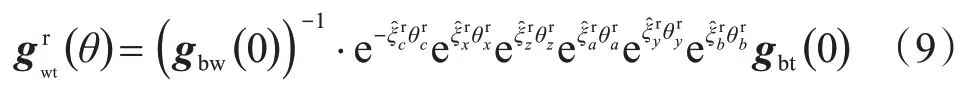
式中：θjr表示實(shí)際情況下j軸的運(yùn)動(dòng)位移；eξ^jrθjr表示實(shí)際情況下j軸的運(yùn)動(dòng)變換矩陣，以A軸為例，實(shí)際情況下A軸的運(yùn)動(dòng)變換矩陣

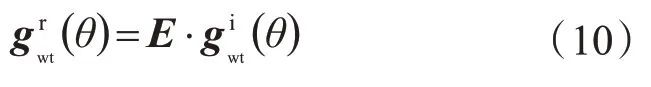
則誤差矩陣E可表示為：

表2 蝸桿砂輪磨齒機(jī)各軸的運(yùn)動(dòng)旋量Table 2 Motion screw of each axis of worm wheel gear grinding machine

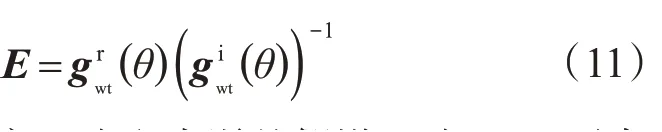
基于六自由度理論和小誤差假設(shè)理論，E又可表示為：

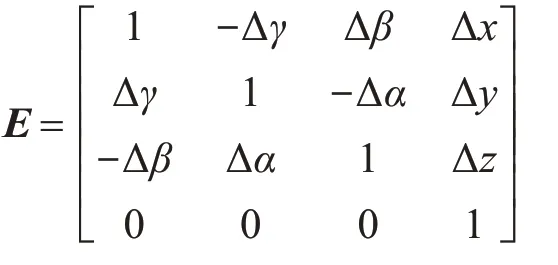
式中：Δx、Δy、Δz，Δα、Δβ、Δγ 分別表示刀具相對(duì)于工件沿X、Y、Z方向的位置誤差分量和角度誤差分量，統(tǒng)稱為空間誤差分量。

2 蝸桿砂輪磨齒機(jī)幾何誤差敏感度系數(shù)計(jì)算

2.1 Sobol法

Sobol法是基于方差分解的改進(jìn)蒙特卡洛方法。采用Sobol 法對(duì)模型Y =f (x)進(jìn)行敏感度分析，其中x=(x1，x2，…，xl)表示l個(gè)輸入?yún)?shù)。在蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析中，以X方向的位置誤差分量Δx為例進(jìn)行分析，Δx與幾何誤差的關(guān)系可表示為：

式中：e = (e1，e2，…，e41)，表示輸入的41項(xiàng)幾何誤差。

根據(jù)Sobol 法的基本原理，對(duì)式（12）進(jìn)行分解，可得：

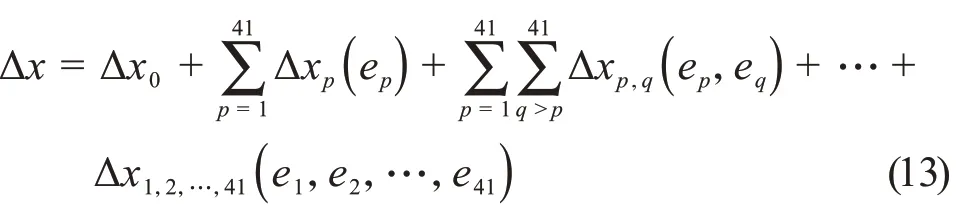
式中：Δx0是基于輸入量的X方向的位置誤差分量Δx的期望值，為常數(shù)；Δxp(ep)表示輸入量ep作用下對(duì)應(yīng)的X方向的位置誤差分量；Δxp，q(ep，eq)表示輸入量ep和eq共同作用下對(duì)應(yīng)的X方向的位置誤差分量，其余高階項(xiàng)以此類推。

式（12）所示模型輸出項(xiàng)的總方差和偏方差分別為：

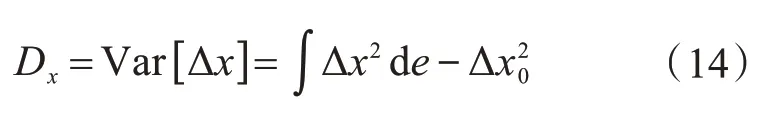
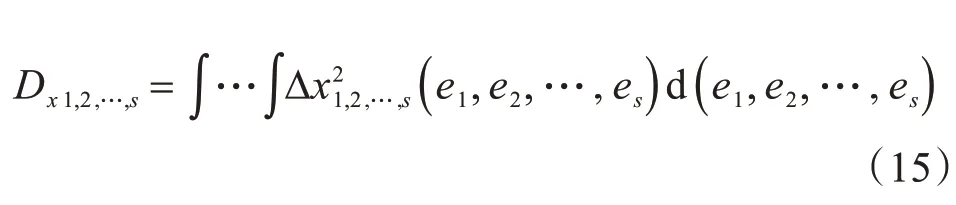
式中：1≤s ≤41。

總方差可分解為：

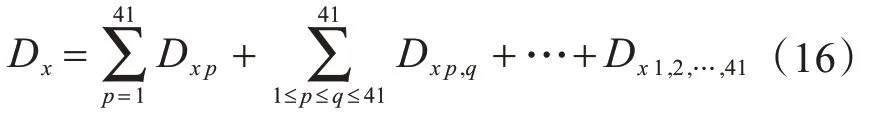
令：

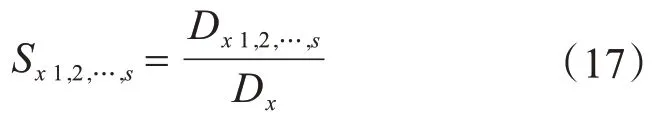
式（16）左右兩邊同時(shí)除以Dx，可得：

式中：Sxp是輸入量ep對(duì)X 方向位置誤差分量的一階敏感度系數(shù)，表示單個(gè)幾何誤差對(duì)X方向位置誤差分量的影響；Sxp，q是輸入量ep和eq對(duì)X方向位置誤差分量的二階敏感度系數(shù)，表示ep和eq共同作用對(duì)X位置誤差分量的影響；其余高階項(xiàng)同理。

在進(jìn)行蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析時(shí)，通常只分析其一階敏感度和全局敏感度，則輸入量ep對(duì)X方向位置誤差分量的一階敏感度系數(shù)可表示為：

輸入量ep對(duì)X方向位置誤差分量的全局敏感度系數(shù)可表示為：

其中：

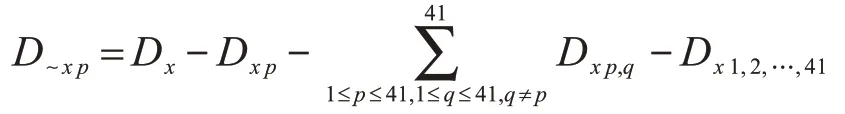
2.2 蒙特卡洛估算

在計(jì)算蝸桿砂輪磨齒機(jī)幾何誤差對(duì)空間誤差分量的敏感度系數(shù)前，需通過(guò)蒙特卡洛采樣方法對(duì)輸入?yún)?shù)進(jìn)行采樣，生成2個(gè)相對(duì)獨(dú)立的采樣矩陣。仍以X方向的位置誤差分量Δx為例進(jìn)行分析，其期望值、方差、偏方差、D～xp的估算公式為：

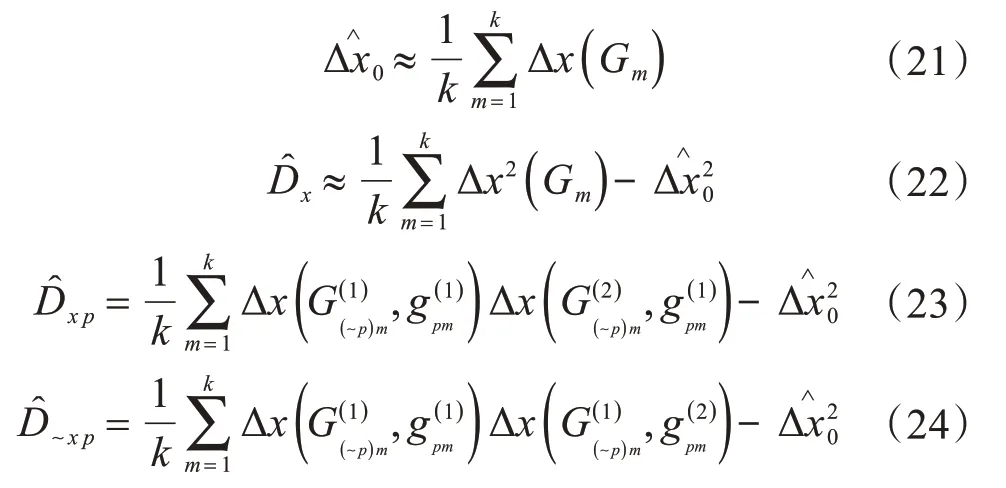
式中：k代表每個(gè)輸入量的采樣個(gè)數(shù)；上標(biāo)(1)，(2)表示2個(gè)采樣矩陣的編號(hào)；Gm表示從采樣空間取得的第m個(gè)采樣集；gpm表示采樣點(diǎn)集中第m個(gè)采樣點(diǎn)的第p個(gè)幾何誤差的值。

將式（21）至（24）代入式（19）、（20）中，即可計(jì)算出蝸桿砂輪磨齒機(jī)幾何誤差對(duì)X方向位置誤差分量的一階敏感度系數(shù)和全局敏感度系數(shù)。

3 蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析實(shí)例

3.1 指令位置分析及幾何誤差采樣

蝸桿砂輪磨齒機(jī)為專用機(jī)床，磨削齒輪時(shí)其運(yùn)動(dòng)軌跡單一。以YW7232型蝸桿砂輪磨齒機(jī)為研究對(duì)象，分析其磨削過(guò)程中各幾何誤差對(duì)空間誤差分量的敏感度。

蝸桿砂輪磨齒機(jī)磨削齒輪時(shí)，齒輪參數(shù)和蝸桿砂輪參數(shù)如表3所示，其中，齒輪和砂輪的旋向均為右旋。蝸桿砂輪磨削運(yùn)動(dòng)包括4個(gè)運(yùn)動(dòng)過(guò)程：砂輪和齒輪的旋轉(zhuǎn)運(yùn)動(dòng)、砂輪徑向進(jìn)給運(yùn)動(dòng)、砂輪軸向沖程運(yùn)動(dòng)和砂輪竄刀運(yùn)動(dòng)。在磨削之前，蝸桿砂輪磨齒機(jī)B軸和C軸的初始角度為0°，A軸旋轉(zhuǎn)角度由齒輪和砂輪的螺旋角確定；在磨削過(guò)程中，X軸進(jìn)給到指定位置后保持靜止，Y 軸和A 軸靜止不動(dòng)，由B 軸、C 軸和Z軸聯(lián)動(dòng)完成磨削過(guò)程。B軸、C軸的轉(zhuǎn)動(dòng)角度以及Z軸的位置都與時(shí)間t有關(guān)：

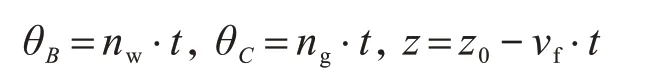
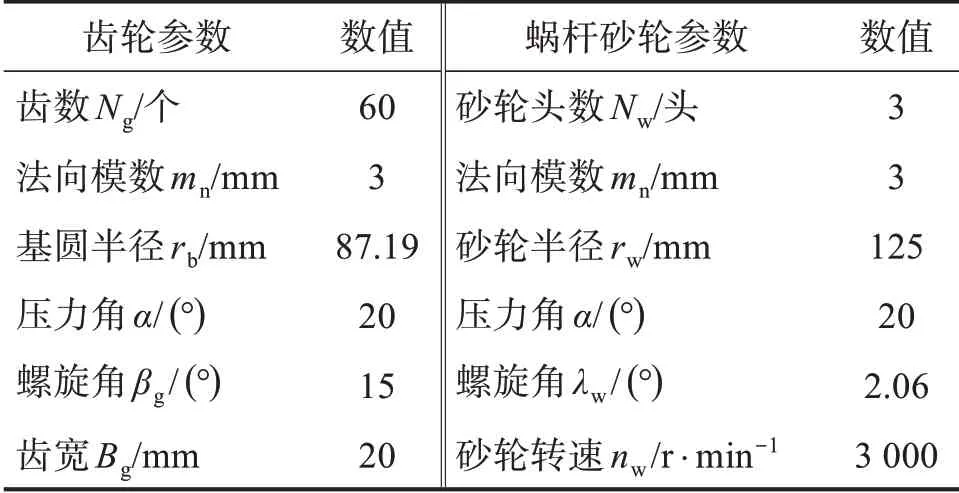
表3 齒輪和蝸桿砂輪參數(shù)Table 3 Parameters of gear and worm wheel

根據(jù)經(jīng)驗(yàn)，取x = 260 mm，z0= 280 mm，假定Y軸在單次磨削過(guò)程中保持靜止，但為了保證砂輪能在整個(gè)刀具長(zhǎng)度方向被充分利用，在多次磨削后砂輪會(huì)發(fā)生沿Y 軸的竄刀運(yùn)動(dòng)，因此分別對(duì)y =-60，- 20，20，60 mm，t = 0，4，8，12，16，20 s 時(shí)對(duì)應(yīng)的24個(gè)機(jī)床指令位置處的幾何誤差項(xiàng)對(duì)空間誤差分量的敏感度進(jìn)行分析。

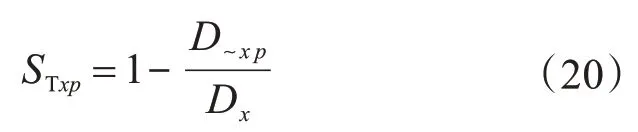
使用Renishaw XL-80激光干涉儀和QC20-W球桿儀對(duì)蝸桿砂輪磨齒機(jī)進(jìn)行多次重復(fù)實(shí)驗(yàn)，測(cè)得機(jī)床的幾何誤差范圍，對(duì)該范圍進(jìn)行合理縮放后得到：位置誤差范圍為0～20 μm，角度誤差范圍為0''～10''，且?guī)缀握`差元素符合正態(tài)分布。

3.2 敏感度分析結(jié)果

分別計(jì)算24個(gè)指令位置處各幾何誤差項(xiàng)對(duì)Δx、Δy、Δz、Δα、Δβ、Δγ 的一階敏感度系數(shù)和全局敏感度系數(shù)，再通過(guò)式（25）和式（26）對(duì)24 個(gè)指令位置處的敏感度系數(shù)求平均數(shù)，可以得到機(jī)床磨削過(guò)程中各幾何誤差項(xiàng)對(duì)空間誤差分量的敏感度系數(shù)，結(jié)果如圖3至圖8所示。

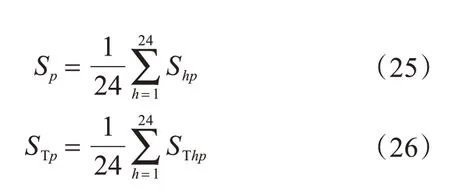
式中：Sp和STp分別表示第p項(xiàng)幾何誤差的一階敏感度和全局敏感度系數(shù)，Shp和SThp分別表示第p項(xiàng)幾何誤差在位置h處的一階敏感度系數(shù)和全局敏感度系數(shù)。

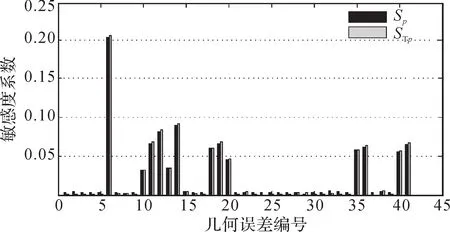
圖3 YW7232型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)X 方向位置誤差分量的敏感度系數(shù)Fig. 3 Sensitivity coefficient of geometric errors to X-direction position error component of YW7232 worm wheel gear grinding machine

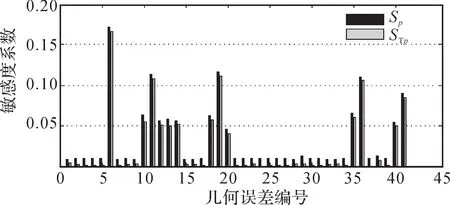
圖4 YW7232 型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)Y 方向位置誤差分量的敏感度系數(shù)Fig. 4 Sensitivity coefficient of geometric errors to Y-direction position error component of YW7232 worm wheel gear grinding machine

基于以上一階敏感度系數(shù)以及全局敏感度系數(shù)計(jì)算結(jié)果，可以得出如下結(jié)論：

1）將敏感度系數(shù)大于0.05的幾何誤差項(xiàng)作為關(guān)鍵幾何誤差項(xiàng)，根據(jù)圖3至圖8可得蝸桿砂輪磨齒機(jī)磨削過(guò)程中對(duì)Δx、Δy、Δz、Δα、Δβ、Δγ影響較大的關(guān)鍵幾何誤差項(xiàng)，如表4所示。

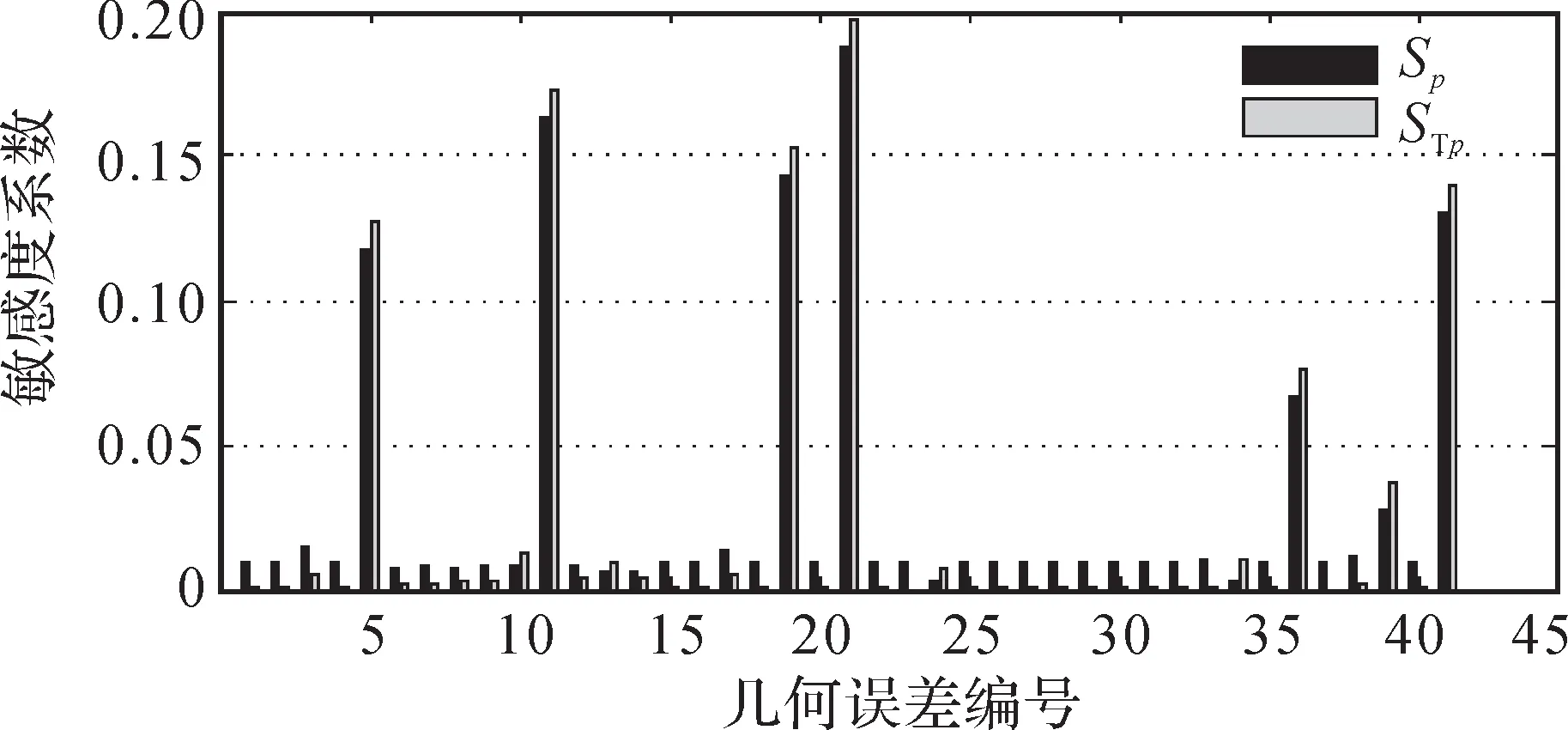
圖5 YW7232 型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)Z 方向位置誤差分量的敏感度系數(shù)Fig. 5 Sensitivity coefficient of geometric errors to Z-direction position error component of YW7232 worm wheel gear grinding machine

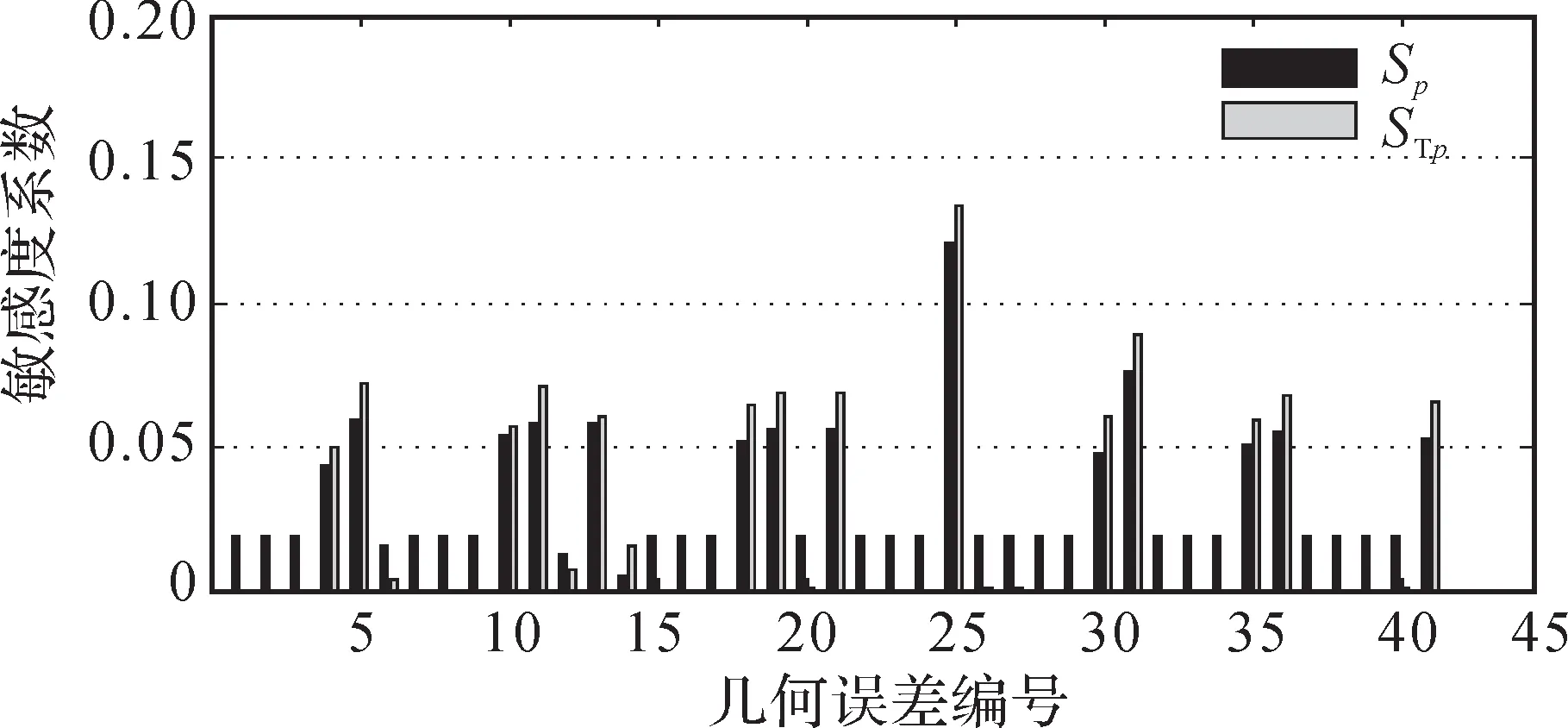
圖6 YW7232型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)X 方向角度誤差分量的敏感度系數(shù)Fig. 6 Sensitivity coefficient of geometric errors to X-direction angular error component of YW7232 worm wheel gear grinding machine

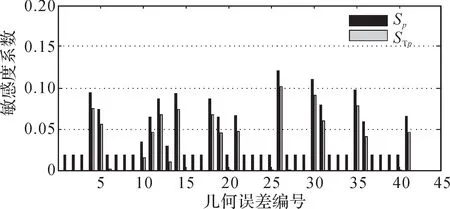
圖7 YW7232 型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)Y 方向角度誤差分量的敏感度系數(shù)Fig. 7 Sensitivity coefficient of geometric errors to Y-direction angular error component of YW7232 worm wheel gear grinding machine

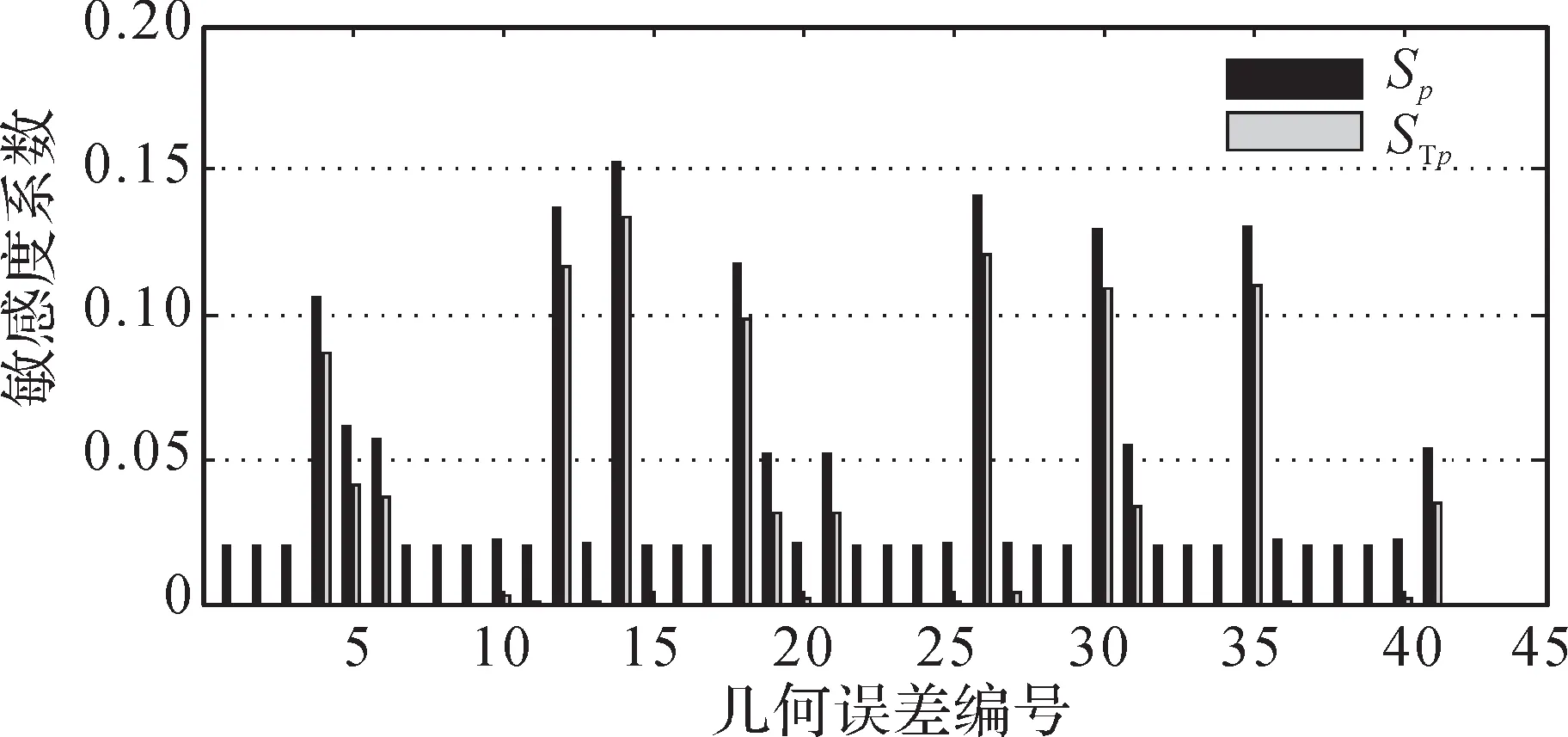
圖8 YW7232 型蝸桿砂輪磨齒機(jī)幾何誤差對(duì)Z 方向角度誤差分量的敏感度系數(shù)Fig. 8 Sensitivity coefficient of geometric errors to Z-direction angular error component of YW7232 worm wheel gear grinding machine

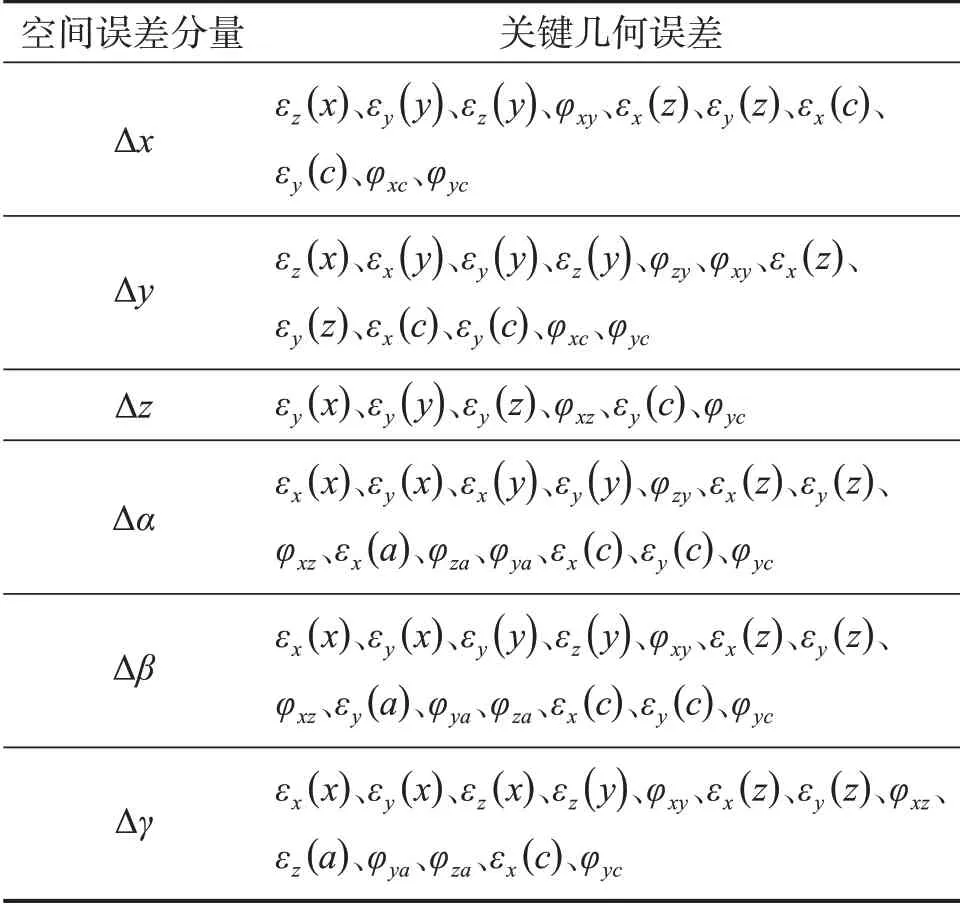
表4 YW7232型蝸桿砂輪磨齒機(jī)的關(guān)鍵幾何誤差項(xiàng)Table 4 Key geometric error terms of YW7232 worm wheel gear grinding machine

2）由表4可知，對(duì)蝸桿砂輪磨齒機(jī)空間誤差分量影響較大的幾何誤差為εx(x)、εy(x)、εz(x)、εx(y)、εy(y)、εz(y)、εx(z)、εy(z)、φxz、φzy、φxy、εx(a)、εy(a)、εz(a)、φza、φya、εx(c)、εy(c)、φxc、φyc，共20項(xiàng)。

3）由圖3至圖8可知，幾何誤差對(duì)Δx、Δy、Δz的全局敏感度系數(shù)和一階敏感度系數(shù)大致相同，而對(duì)Δα、Δβ、Δγ的全局敏感度系數(shù)和一階敏感度系數(shù)有差別，說(shuō)明幾何誤差之間的耦合作用對(duì)位置誤差分量的影響比對(duì)角度誤差分量的影響小。

4）對(duì)空間誤差分量影響較大的是角度誤差，而定位誤差和直線度誤差對(duì)空間誤差分量的影響較小，與角度誤差相比可以忽略不計(jì)，但角度誤差比定位誤差和直線度誤差更難補(bǔ)償，因此，在機(jī)床設(shè)計(jì)和制造階段識(shí)別關(guān)鍵幾何誤差是很有必要的，可以從根本上提高機(jī)床的精度。

4 蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析結(jié)果驗(yàn)證與討論

為了驗(yàn)證蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析結(jié)果的正確性，對(duì)機(jī)床關(guān)鍵幾何誤差進(jìn)行修正，并對(duì)比修正前后機(jī)床空間誤差分量以及機(jī)床聯(lián)動(dòng)運(yùn)動(dòng)軌跡。首先，對(duì)比關(guān)鍵幾何誤差修正前后機(jī)床空間誤差分量，把影響某一空間誤差分量的關(guān)鍵幾何誤差項(xiàng)修正為0，其他誤差項(xiàng)保持不變，對(duì)比修正前后X、Y、Z三個(gè)方向的位置誤差分量和角度誤差分量，修正后空間誤差分量越小，表明修正的幾何誤差對(duì)空間誤差分量的影響越大。

以y = 20 mm為例，計(jì)算在t =1-20 s時(shí)關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)的空間誤差分量，結(jié)果如圖9至圖14所示。

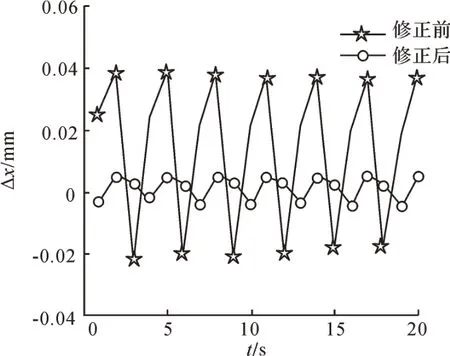
圖9 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)X方向位置誤差分量Fig. 9 X-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

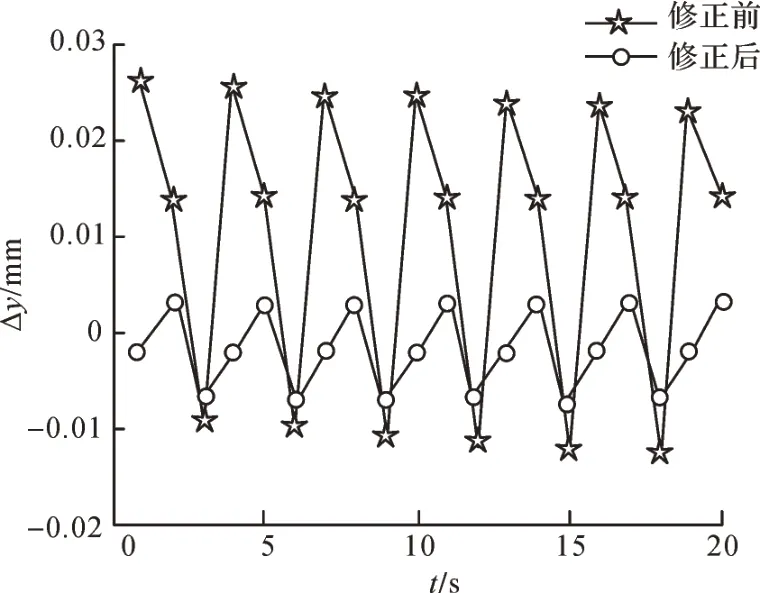
圖10 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)Y 方向位置誤差分量Fig. 10 Y-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

由圖9 至圖14 可知，對(duì)影響蝸桿砂輪磨齒機(jī)空間誤差分量的關(guān)鍵幾何誤差項(xiàng)進(jìn)行修正后，蝸桿砂輪磨齒機(jī)X、Y、Z方向的位置誤差分量和角度誤差分量都明顯減小，且接近于0，說(shuō)明修正的幾何誤差項(xiàng)對(duì)蝸桿砂輪磨齒機(jī)空間誤差分量的影響很大，證明了敏感度分析結(jié)果的正確性。

其次，對(duì)比關(guān)鍵幾何誤差修正前后機(jī)床聯(lián)動(dòng)運(yùn)動(dòng)軌跡。對(duì)20項(xiàng)關(guān)鍵幾何誤差進(jìn)行修正后，在機(jī)床常用的加工區(qū)間內(nèi)通過(guò)仿真模擬球桿儀的3種測(cè)量模式：X-Y-C 聯(lián)動(dòng)測(cè)量模式、X-Z 聯(lián)動(dòng)測(cè)量模式和Y-Z聯(lián)動(dòng)測(cè)量模式，并對(duì)比修正前后的球桿儀的桿長(zhǎng)。3種測(cè)量模式示意圖及關(guān)鍵幾何誤差修正前后球桿儀的桿長(zhǎng)對(duì)比如圖15 至圖17 所示。圖中標(biāo)準(zhǔn)圓的半徑為球桿儀的標(biāo)準(zhǔn)長(zhǎng)度，記為100 mm，圖中一個(gè)刻度代表0.01 mm。

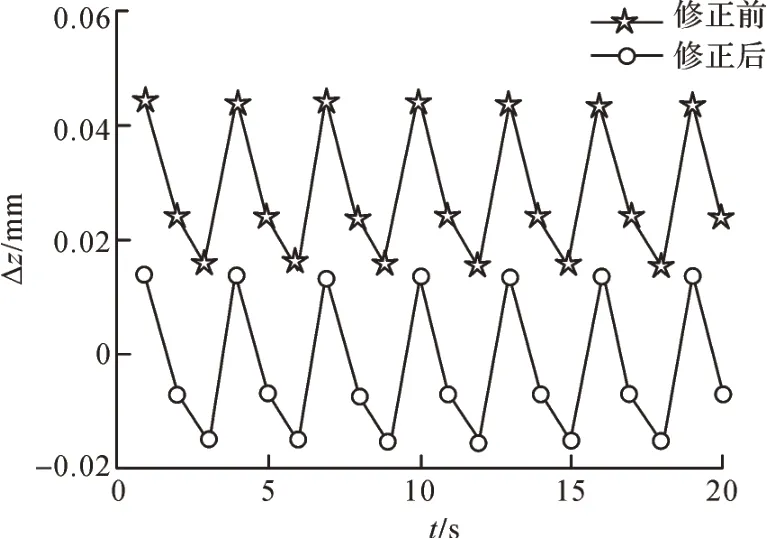
圖11 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)Z 方向位置誤差分量Fig. 11 Z-direction position error component of worm wheel gear grinding machine before and after key geometric error correction

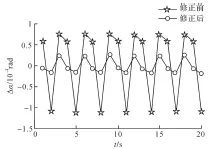
圖12 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)X 方向角度誤差分量Fig. 12 X-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

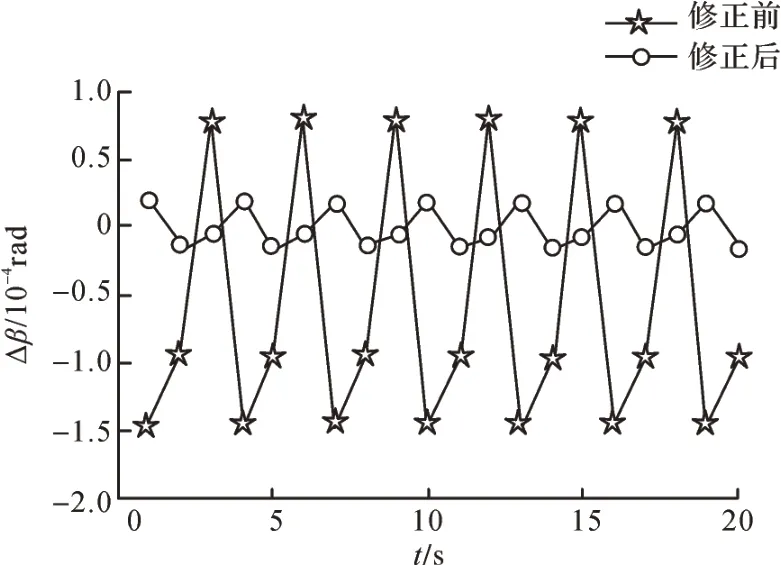
圖13 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)Y 方向角度誤差分量Fig. 13 Y-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

由圖15至圖17可知，對(duì)關(guān)鍵幾何誤差進(jìn)行修正后，蝸桿砂輪磨齒機(jī)的聯(lián)動(dòng)精度明顯改善，這說(shuō)明通過(guò)敏感度分析結(jié)果對(duì)機(jī)床進(jìn)行精度設(shè)計(jì)和誤差補(bǔ)償，可以高效快速地提高機(jī)床空間精度。

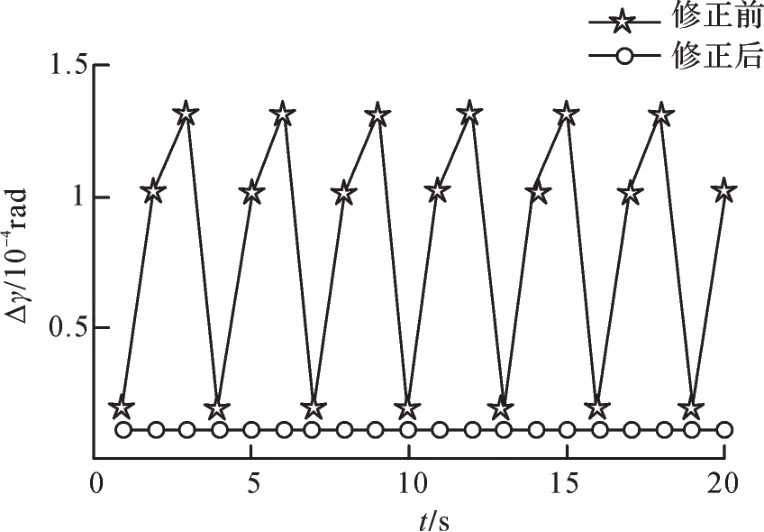
圖14 關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)Z 方向角度誤差分量Fig. 14 Z-direction angular error component of worm wheel gear grinding machine before and after key geometric error correction

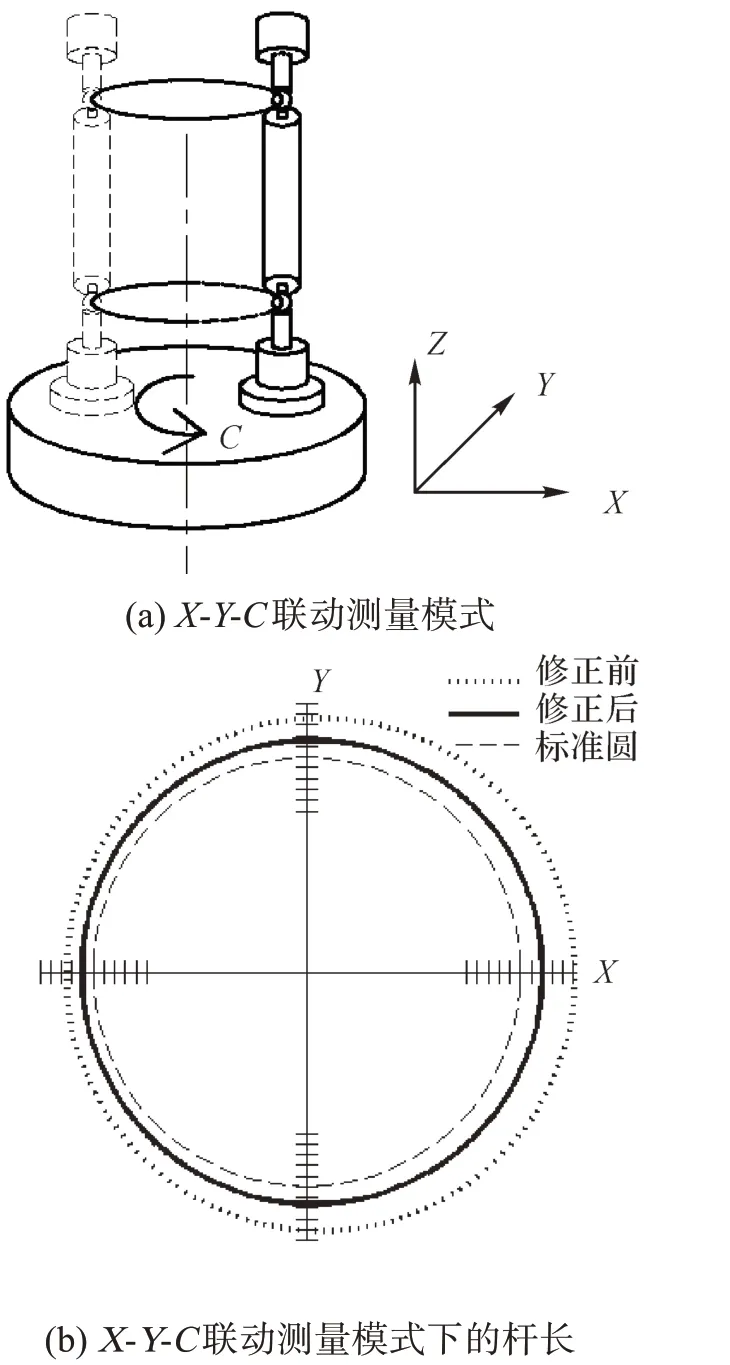
圖15 X-Y-C聯(lián)動(dòng)測(cè)量模式及該模式下球桿儀的桿長(zhǎng)Fig. 15 X-Y-C linkage measurement mode and rod length of ballbar in this mode

5 結(jié) 論

本文針對(duì)蝸桿砂輪磨齒機(jī)結(jié)構(gòu)復(fù)雜、幾何誤差種類多引起的建模困難、幾何誤差測(cè)量及補(bǔ)償復(fù)雜的問(wèn)題，提出了一種基于旋量理論和Sobol法的蝸桿砂輪磨齒機(jī)幾何誤差敏感度分析方法。

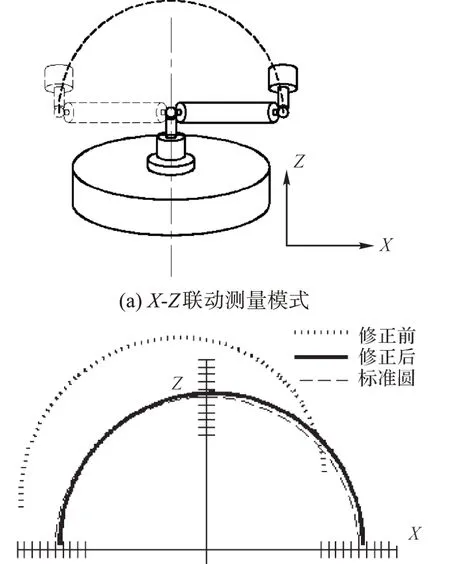
(b) X-Z聯(lián)動(dòng)測(cè)量模式下的桿長(zhǎng)圖16 X-Z聯(lián)動(dòng)測(cè)量模式及該模式下球桿儀的桿長(zhǎng)Fig. 16 X-Z linkage measurement mode and rod length of ballbar in this mode

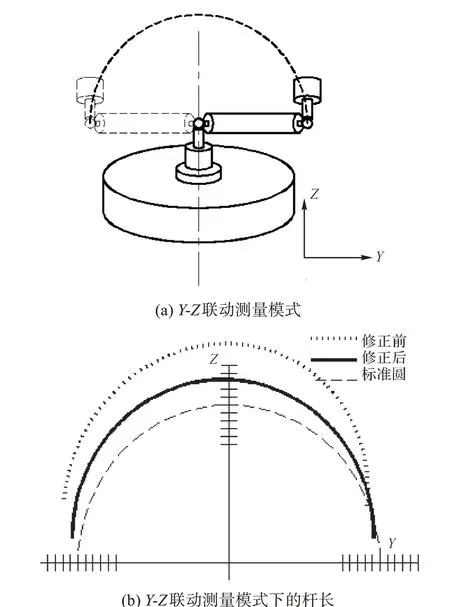
圖17 Y-Z聯(lián)動(dòng)測(cè)量模式及該模式下球桿儀的桿長(zhǎng)Fig. 17 Y-Z linkage measurement mode and rod length ofballbar in this mode

1）基于旋量理論，建立了蝸桿砂輪磨齒機(jī)幾何誤差模型。

2）基于Sobol法，計(jì)算了蝸桿砂輪磨齒機(jī)磨削過(guò)程中各幾何誤差對(duì)空間誤差分量的敏感度系數(shù)，識(shí)別出影響機(jī)床空間誤差分量的關(guān)鍵幾何誤差項(xiàng)。

3）通過(guò)仿真分析，對(duì)比了關(guān)鍵幾何誤差修正前后蝸桿砂輪磨齒機(jī)的空間誤差分量和3種測(cè)量模式下球桿儀的桿長(zhǎng)，驗(yàn)證了敏感度分析結(jié)果的有效性。

4）根據(jù)敏感度分析結(jié)果，對(duì)機(jī)床進(jìn)行誤差測(cè)量和補(bǔ)償，可高效快速地提高機(jī)床空間精度；將敏感度分析結(jié)果用于指導(dǎo)機(jī)床設(shè)計(jì)與裝配，可從根源上改善機(jī)床空間精度。