改進人工蜂群算法優化的LSSVM在混合氣體定量分析中的應用

李成兵，葉 超，毛熙皓

（西南石油大學機電工程學院，四川成都610500）

易燃易爆氣體泄漏引發的燃燒和爆炸事故在石油化工、交通運輸等行業時有發生。常見的易燃易爆氣體有酒精氣體、甲烷、一氧化碳和氫氣等，一般情況下，泄漏的易燃易爆氣體并非單一性質氣體，而是幾種氣體的混合體。因此，對易燃易爆混合氣體進行定量分析具有非常重要的意義，但因各氣體傳感器間存在交叉敏感性［1］，不能實現對各組分氣體濃度的精確測量。目前，提高混合氣體中各組分氣體濃度測量精度的方法主要有支持向量機（support vector machine，SVM）［2-3］、最小二乘支持向量機［4-7］和BP（back propagation，反向傳播）神經網絡［8-11］等。金翠云等人［2］利用PSO 算法對SVM 的參數進行了優化，并將優化后的SVM應用于氣體定量分析，減小了測量誤差。曲健等人［3］利用自適應PSO算法優化了SVM的參數，并與利用遺傳算法優化的結果進行對比，發現采用自適應PSO 算法時分析模型的建模時間較長，但預測精度較高。曾燕等人［4］將LSSVM應用于下水道可燃氣體的定量分析。李玉軍等人［5］將PSO 算法與LSSVM 相結合，建立了混合氣體定量分析模型，提高了混合氣體中各組分氣體濃度的測量精度。丁續達等人［6］利用LSSVM對燃煤發電排放的NOx的濃度進行了在線預測。丁知平等人［7］使用引力算法優化了LSSVM，從而提高了NOx濃度的預測精度。王春晨等人［8］將BP神經網絡與PID（proportion integration differentiation，比例積分微分）控制器相結合，實現混合氣體的配比。張瑞華［9］通過BP人工神經網絡建立了一定濃度可燃混合氣體的爆炸超壓模型。黃偉軍等人［10］改進了BP神經網絡，實現了汽車尾氣各組分氣體濃度的測量。龔雪飛等人［11］利用PSO算法對BP神經網絡進行優化，實現了多元有害氣體的濃度測量，并提高了測量精度。BP神經網絡的收斂精度和預測精度與其網絡結構的選擇有很大關系，因此其輸出具有不可預測性和不一致性，且BP神經網絡的本質為梯度下降法，其學習的時間較長，而LSSVM可以很好地避開上述問題。

為此，筆者提出一種利用改進人工蜂群算法優化LSSVM的方法，對含有酒精氣體、甲烷、一氧化碳和氫氣的混合氣體進行定量分析。首先，通過在標準人工蜂群算法中引入自適應遞減因子以更新搜索步長，并結合輪盤賭與反向輪盤賭機制來改進待工蜂跟隨概率公式，以提高搜索精度；然后，利用IABC算法對LSSVM 的懲罰參數C 和核參數σ2進行優化，使LSSVM擁有具有更高的計算精度；最后，將優化后的LSSVM用于混合氣體定量分析，以提高在交叉敏感狀態下混合氣體中各組分氣體濃度的測量精度。

1 最小二乘支持向量機

最小二乘支持向量機（LSSVM）是由Suykens等［12］在SVM的基礎上提出的，將SVM中的不等式約束轉變為等式約束，并選取誤差平方和作為優化目標函數，使得二次規劃問題轉化為線性方程組求解問題，從而降低了計算難度。LSSVM在非線性系統建模方面更具有優勢［13-14］，其基本思想如下。

給定一個訓練數據集T ={( xi，yi)|i=1，2，…，l }，其中輸入為n維向量xi，輸出為yi，l為訓練樣本個數，則LSSVM的優化問題可以描述為：

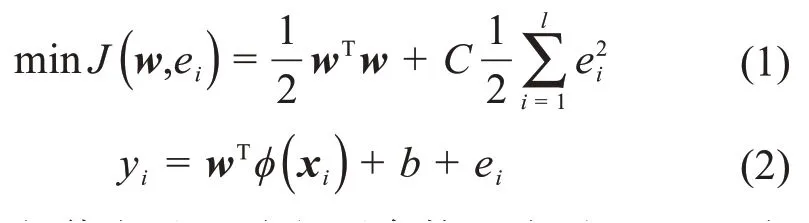
式中：w為權值向量，C為懲罰參數，ei為誤差，φ(·)為原空間到高維空間的非線性映射，b為閾值。

由于w可能有無限的維數，直接求解式（1）較為困難，因此引入拉格朗日函數：

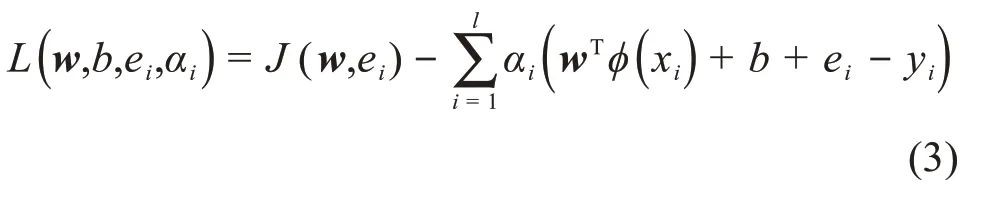
式中：αi≥0，為拉格朗日乘子。

根據取極值的必要條件，設拉格朗日函數對于各個變量的偏導數為零，可得：

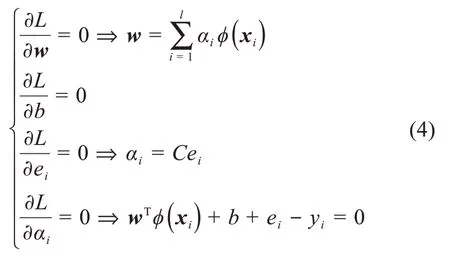
引入核函數：

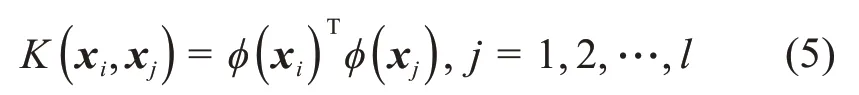
基于核函數，可將式（4）整理為：

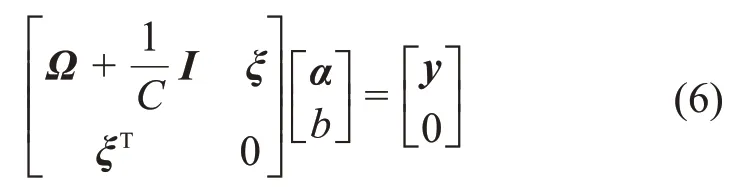
式中：Ω 為一個方陣，其第i 行第j 列元素Ωij=K ( xi，xj)；I為單位矩陣；ξ =[1，…，1]T。

本文選擇徑向基函數作為核函數：

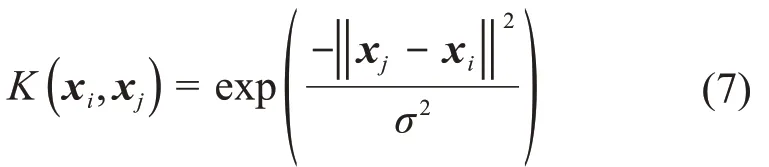
式中：σ2為核寬度。

根據式（6）求出的α 和b 構造用于函數估計的LSSVM模型：

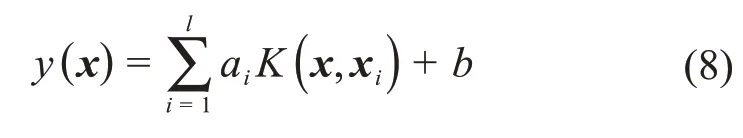
2 人工蜂群算法

2.1 標準人工蜂群算法

標準人工蜂群（ABC）算法于2005年由Karaboga提出［15］，常用于求解函數極值問題。在標準ABC算法中，蜂群由3 種蜂組成：采蜜蜂、待工蜂、偵查蜂。采蜜蜂搜索蜜源，測量蜜源質量即適應度函數值，并將蜜源信息分享給其他蜜蜂；待工蜂通過采蜜蜂分享的信息，以一定的概率選擇蜜源進行搜索；偵查蜂隨機搜索蜜源。

標準ABC算法實現的具體步驟如下［16-18］：

1）初始化蜜蜂種群。初始時刻所有蜜蜂均為偵查蜂，全局隨機搜索蜜源，蜜源的位置代表空間內的可能解向量，蜜源的初始位置在搜索空間隨機產生，隨機產生的公式為：

式中：蜜源m（m=1，2，…，N）與蜜蜂一一對應，N為蜜源即蜜蜂個數；Xnm表示蜜源位置，Xnmax和Xnmin分別表示搜索空間的上限和下限，n=1，2，…，D，D 為優化問題參量的個數；rand（0,1）為［0,1］內的隨機數。

搜索到蜜源初始位置后，所有偵查蜂轉變為采蜜蜂，并測量每個蜜源的適應度函數值（用于衡量蜜源的質量），然后采蜜蜂在蜜源初始位置鄰域內搜索新蜜源：

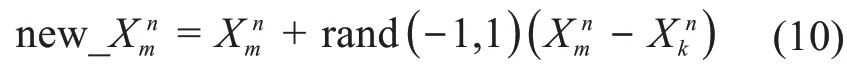
式中：k∈｛1，2，…，N｝，且k≠m；rand（-1，1）為［-1，1］內的隨機數。

當新蜜源的適應度函數值優于舊蜜源的適應度函數值時，根據貪婪準則，以新蜜源取代舊蜜源，否則保留舊蜜源。

2）對所有采蜜蜂測量得到的適應度函數值進行排序，排名靠后的采蜜蜂成為待工蜂，一般定義待工蜂和采蜜蜂各占種群一半。然后，采蜜蜂飛回交流區把蜜源信息分享給待工蜂，待工蜂依據輪盤賭機制對蜜源進行選擇，選擇概率為：

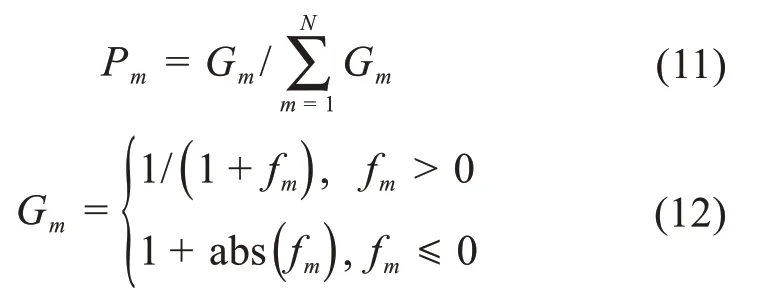
式中：Gm為解的適應度函數值，fm為目標函數值。

對于每只待工蜂，在選擇一個蜜源后，按式（10）在該蜜源鄰域內尋找其他蜜源，若新蜜源的適應度函數值更優，則取代原蜜源，且該待工蜂轉換為采蜜蜂。

對于每只采蜜蜂，在分享信息后，繼續在該蜜源附近尋找新蜜源并計算其適應度函數值，然后根據貪婪準則進行選取。

3）若在搜索過程中，經過s次搜索并得到一定的搜索閾值T后仍沒有找到更優的蜜源，則采蜜蜂和待工蜂將放棄該蜜源且轉變為偵查蜂，并按式（9）重新隨機產生一個新的蜜源。

2.2 改進的人工蜂群算法

在標準ABC算法中，蜂群搜索的范圍和精度由步長rand（-1，1）決定：當rand（-1，1）較大時，算法收斂速度較快，但隨著優化趨近最優值，容易跳過全局最優解；當rand（-1，1）較小時，算法收斂速度較慢，但收斂精度高。對標準ABC算法分析可知，在搜索前期，應取較大的步長，以保證收斂速度，加快向最優解靠攏；在搜索后期，算法搜索到的值逐漸靠近最優解，應逐漸減小步長以實現對最優解周圍進行細化搜索，減少在最優值附近的動蕩，提高收斂精度。基于此，引入了一種自適應遞減因子來更新搜索步長，其公式為：

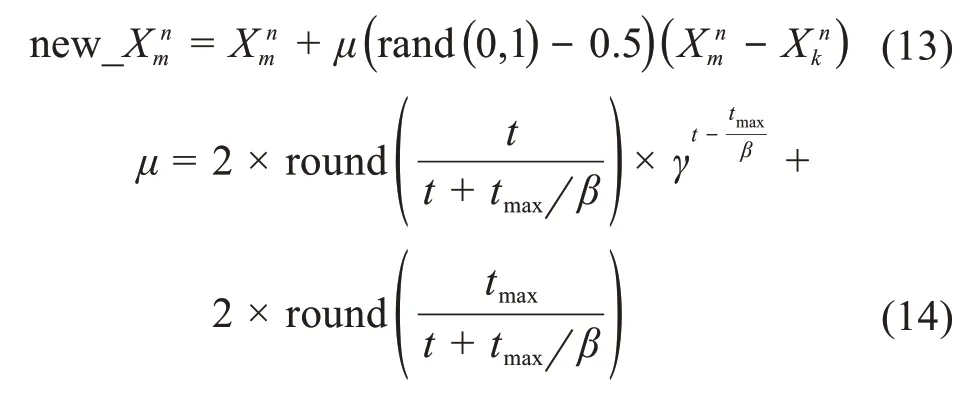
式中：μ為自適應遞減因子，round（）為四舍五入函數，t為當前迭代次數，tmax為最大迭代次數，β ∈(1，tmax)且? 不為整數，γ ∈(0，1)。

設tmax=100，當β和γ取不同值時，μ與迭代次數的關系曲線如圖1所示。

由圖1 可以看出，當γ 相同時，β 值越小，維持大步長的迭代次數越多，說明算法在搜索前期的收斂速度較快；當β相同時，γ值越小，達到最大迭代次數時μ越小，說明算法在搜索后期的收斂精度更高。

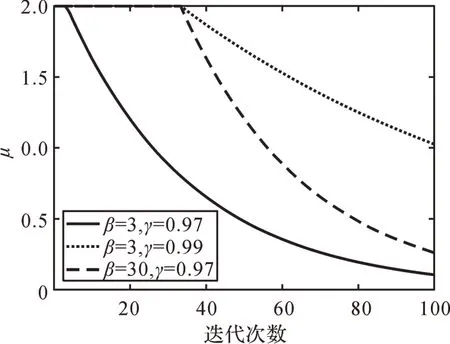
圖1 β、γ不同時μ與迭代次數的關系曲線Fig. 1 The relationship between μ and iteration times under different β and γ

同時，在標準ABC算法中，待工蜂按照式（11）對蜜源進行選擇，適應度越高的蜜源被選擇的概率越大，但這種選擇方式會使蜂群在優化過程中朝著適應度高的蜜源集中，而適應度低的蜜源則會被迅速淘汰，這會導致蜂群多樣性降低，使得種群早熟收斂而不能達到全局最優。因此，在算法搜索前期應使待工蜂對適應度高的蜜源進行搜索，以保證收斂速度，而在算法搜索后期應使待工蜂對適應度低的蜜源進行適當的跟蹤搜索，以保持種群的多樣性，避免陷入局部最優。為此，引進反向輪盤賭機制［19］，并結合輪盤賭和反向輪盤賭，改進待工蜂的跟隨概率公式，具體改進公式為：

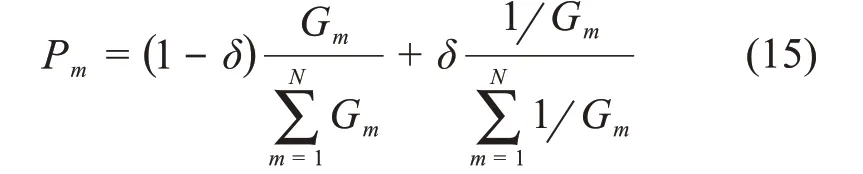
式中

改進后，既保證了算法在搜索前期對高適應度蜜源搜索的收斂速度，又增大了搜索后期稍差適應度蜜源的被選擇概率，保持了蜂群的多樣性，提高了算法的求泛能力。

3 實驗驗證

3.1 改進人工蜂群算法性能測試

為測試IABC算法的性能（主要為收斂精度），選取5個常用測試函數進行實驗，并與PSO算法進行對比。常用的5個測試函數如表1所示，每個函數的最優值均為0，其中：測試函數Sphere 的搜索范圍為［-100，100］，Schaffer 的搜索范圍為［-100，100］，Schwefel 的搜索范圍為［-500，500］，Griewank 的搜索范圍為［-600，600］，Rosenbrock 的搜索范圍為［-2.048，2.048］。

表1 常用的5個測試函數Table 1 Five commonly used test functions

設IABC算法的種群規模為20，維數為2，最大迭代次數tmax=100，搜索閾值T=10，γ=0.92，β=1.3。設PSO 算法的種群規模為20，維數為2，最大迭代次數為100，慣性權重因子為0.8，學習因子c1=1.5，c2=1.8。使用MATLAB R2017b進行實驗測試，每種優化算法對每個測試函數進行10 次實驗，測試結果如表2 所示。通過對比表2中最優值、最劣值和平均值可以看出：IABC 算法對5個測試函數的收斂精度要比PSO算法高，且收斂效果更好。

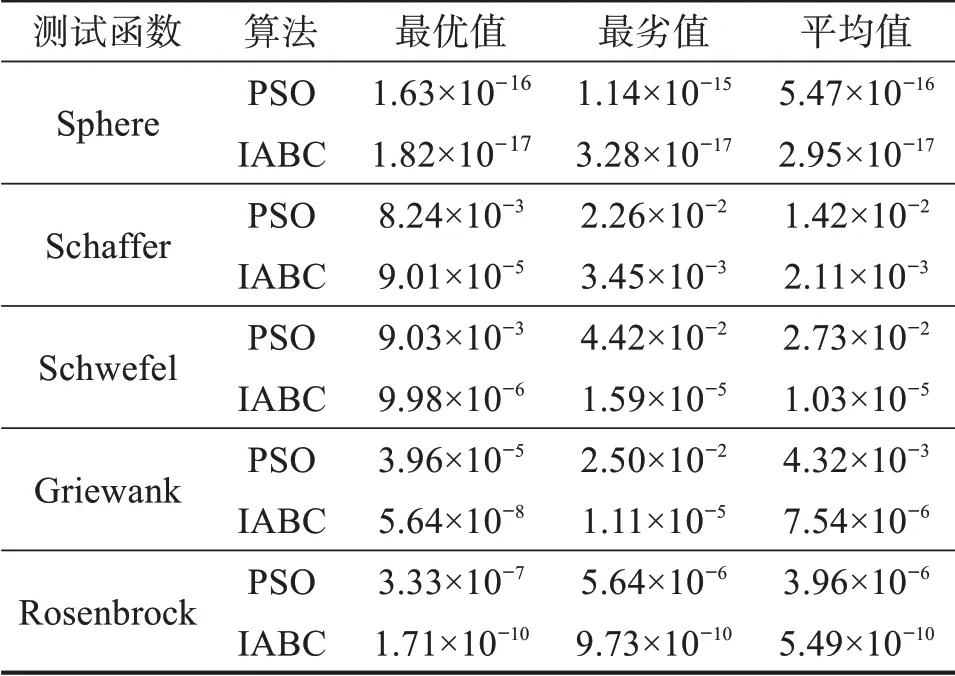
表2 IABC算法和PSO算法的性能測試結果對比Table 2 Comparison of performance test results between IABC algorithm and PSO algorithm

同時，為評價IABC 算法和PSO 算法的復雜度，通過計算各算法的運行時間來對比其復雜度［20］。分別使用IABC 算法和PSO 算法對5 個測試函數進行1 000次迭代，采用高迭代次數是為了使2種算法的優化時間的差異更加顯著。每個測試函數進行10次測試，并計算2種算法的平均優化時間，結果如圖2所示。由圖可知，IABC算法迭代1 000次所用的時間分別為：3.351 s（函數Sphere）、4.447 s（函數Schaffer）、4.361 s（函數Schwefel）、4.099 s（函數Griewank）、4.663 s（函數Rosenbrock），均略低于PSO算法的優化時間（3.459 s（函數Sphere）、4.972 s（函數Schaffer）、4.615 s（函數Schwefel）、4.273 s（函數Griewank）、5.314 s（函數Rosenbrock））。通過對比2種算法的優化時間可知，IABC 算法的迭代速度稍高于PSO 算法，說明計算過程中IABC 算法的復雜度低于PSO算法。

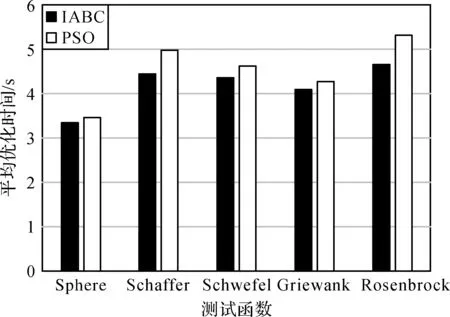
圖2 IABC算法和PSO算法優化時間對比Fig. 2 Comparison of optimization time between IABC algorithm and PSO algorithm

3.2 混合氣體定量分析實驗

在20℃、相對濕度為50%的環境下對包含酒精氣體、甲烷、一氧化碳和氫氣的混合氣體進行濃度檢測。酒精氣體、甲烷、一氧化碳、氫氣四種氣體的濃度范圍分別為：190～770，260～400，110～470，15～45 mg/m3。實驗中使用的傳感器為：鄭州煒盛電子科技有限公司生產的MQ-3B 酒精傳感器，檢測濃度范圍為47.8～956.7 mg/m3；MQ-4 甲烷傳感器，檢測濃度范圍為199.7～6 655.3 mg/m3；MQ-7B一氧化碳傳感器，檢測濃度范圍為11.6～582.3 mg/m3；MQ-8氫氣傳感器，檢測濃度范圍為8.3～83.2 mg/m3。選用的傳感器皆為半導體電阻式傳感器，各傳感器的電導率隨著待測氣體濃度的增大而增大，擁有較高的靈敏度。采用STM32F103VET6作為單片機最小系統，測試系統原理圖和測試環境分別如圖3和圖4所示。

采集各組分濃度不同的混合氣體以及傳感器響應值，共計得到50組樣本數據，取其中40組樣本數據作為訓練樣本，剩余10組作為測試樣本。為使數據更符合算法的輸入，需對獲取的原始樣本進行歸一化處理（將樣本數據歸一化到［0，1］內），歸一化公式如下：

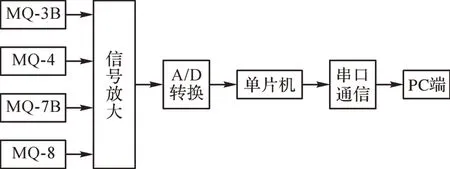
圖3 混合氣體濃度測試系統原理圖Fig. 3 Schematic diagram of mixture gas concentration test system

圖4 混合氣體濃度測試環境Fig. 4 Mixture gas concentration test environment

式中：Uq是采集到的樣本數據，Uqmax、Uqmin為數據樣本中最大值和最小值。

利用LSSVM 建立混合氣體定量分析模型前需對其懲罰參數C和核參數σ2進行合理的優化選擇，本文采用IABC算法對懲罰參數和核參數進行尋優，并與常用的混合氣體定量分析方法——PSO算法的尋優結果進行對比，具體的尋優過程如下：

1）對LSSVM 的懲罰參數C 和核參數σ2進行初始化，初步建立回歸模型。

2）初始化IABC 算法的種群規模、最大迭代次數、搜索閾值、自適應因子等參數以及懲罰參數C和核參數σ2的搜索范圍。

3）將模型輸出結果的均方誤差作為IABC 算法的適應度值，并設定合適的均方誤差作為閾值。

4）執行IABC算法，記錄并更新最優解。

5）判斷優化結果是否滿足設定的均方誤差或者達到最大迭代次數，若滿足則輸出最優解，即輸出最佳的C和σ2，否則轉第4）步。

為提高測量精度，利用LSSVM分別構建酒精氣體、甲烷、一氧化碳和氫氣的定量分析模型，然后再利用IABC 算法對各組分氣體定量分析模型的參數分別進行優化。以甲烷氣體定量分析模型的參數優化為例，設IABC算法的種群規模為20，維數為2，最大迭代次數為100，搜索閾值為10，γ=0.92，β=1.3；LSS-VM 懲罰參數C 和核參數σ2的搜索范圍設置為（0，100）。根據上述的模型優化流程進行分析，得到基于IABC 算法的甲烷氣體定量分析模型參數優化誤差曲線，如圖5所示。

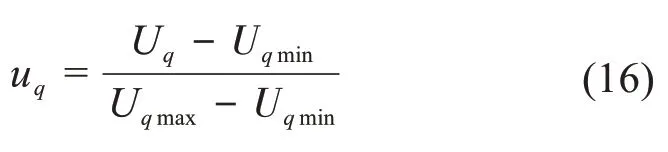
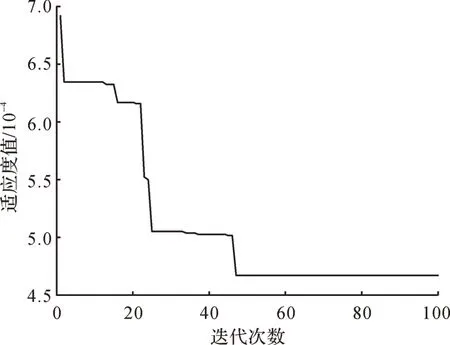
圖5 基于IABC 算法的甲烷氣體定量分析模型參數優化誤差曲線Fig. 5 Optimization error curve of parameters of quantitative analysis model for methane gas based on IABC algorithm

從圖5可以看出，IABC算法在經過46次迭代后便找到了最優解，具有較快的收斂速度。IABC算法迭代100 次所用的時間為7.840 s，此時均方誤差最小，為4.642×10-4，懲罰參數C=58.260，核參數σ2=9.124。用同樣的方法對酒精氣體、一氧化碳和氫氣的定量分析模型進行優化，得到對應的懲罰參數、核參數、均方誤差以及迭代時間，如表3所示。

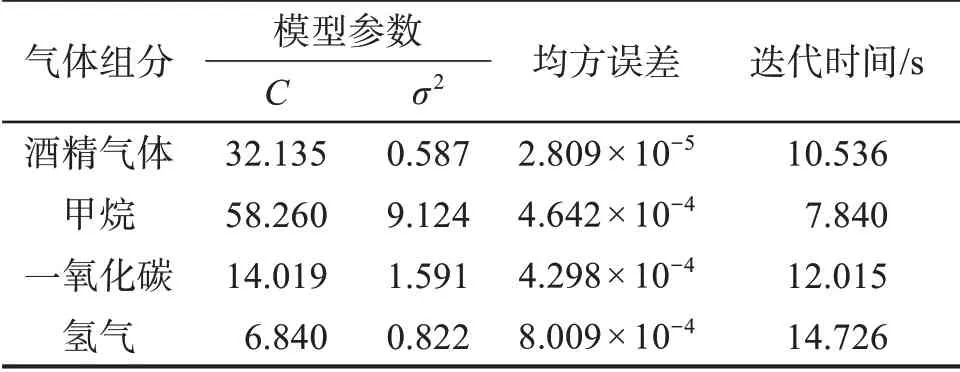
表3 IABC 算法對各組分氣體定量分析模型參數的優化結果Table 3 Optimization results of parameters of quantitative analysis model for each component gas by IABC algorithm

同樣地，采用PSO 算法對各組分氣體定量分析模型進行參數優化。本文設PSO 算法種群規模、維數及最大迭代次數均與IABC 算法相同，分別為20，2，100；PSO 算法慣性權重因子為0.8，學習因子c1=1.5，c2=1.8。PSO 算法的優化流程如圖6 所示，基于PSO算法的甲烷氣體定量分析模型參數優化誤差曲線如圖7所示。

由圖7 可以看出，PSO 算法在經過51 次迭代后找到了最優解，PSO 算法迭代100 次所用的時間為13.021 s，收斂速度稍慢于IABC 算法。此時均方誤差 為3.247×10-3，懲 罰 參 數C=39.331，核 參 數σ2=0.845。用同樣的方法對酒精氣體、一氧化碳和氫氣的定量分析模型進行優化，得到對應的懲罰參數、核參數、均方誤差以及迭代時間，如表4所示。

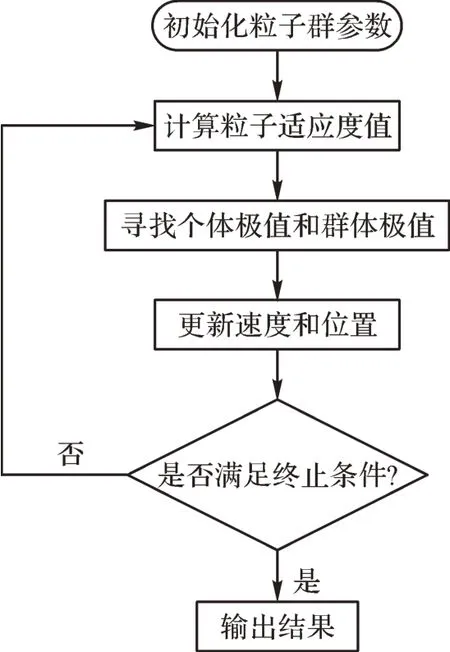
圖6 PSO算法優化流程Fig. 6 Optimization process of PSO algorithm

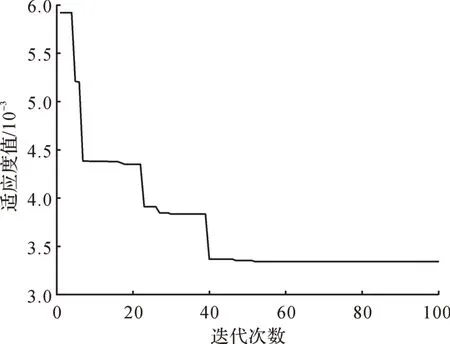
圖7 基于PSO 算法的甲烷氣體定量分析模型參數優化誤差曲線Fig. 7 Optimization error curve of parameters of quantitative analysis model for methane gas based on PSO algorithm

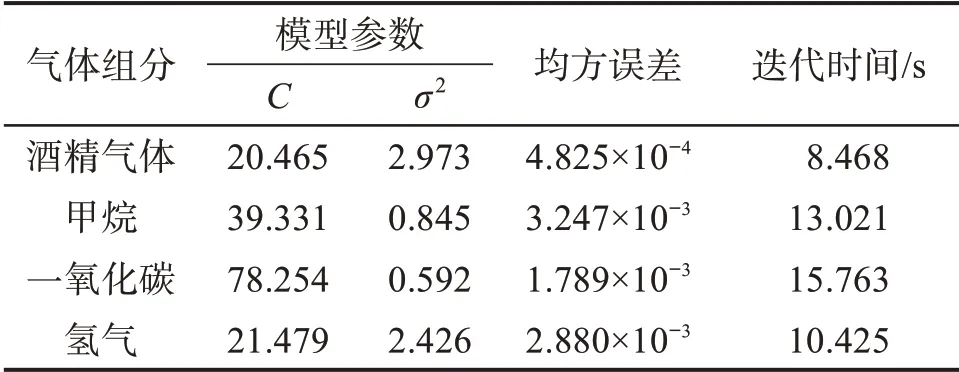
表4 PSO 算法對各組分氣體定量分析模型參數的優化結果Table 4 Optimization results of parameters of quantitative analysis model for each component gas by PSO algorithm

結合表3、表4可以看出，IABC算法對各組分氣體定量分析模型的優化時間總和為45.117 s，PSO算法對各組分氣體定量分析模型的優化時間總和為47.677 s，IABC算法所用的時間略短于PSO算法，且IABC算法對各組分氣體定量分析模型參數進行優化后得到的均方誤差明顯小于PSO算法。將優化得到的懲罰參數和核參數代入LSSVM以重建各組分氣體定量分析模型，并對各測試樣本的氣體濃度進行預測，基于2種算法的混合氣體各組分濃度的預測結果如表5所示，預測相對誤差分別如圖8和圖9所示。

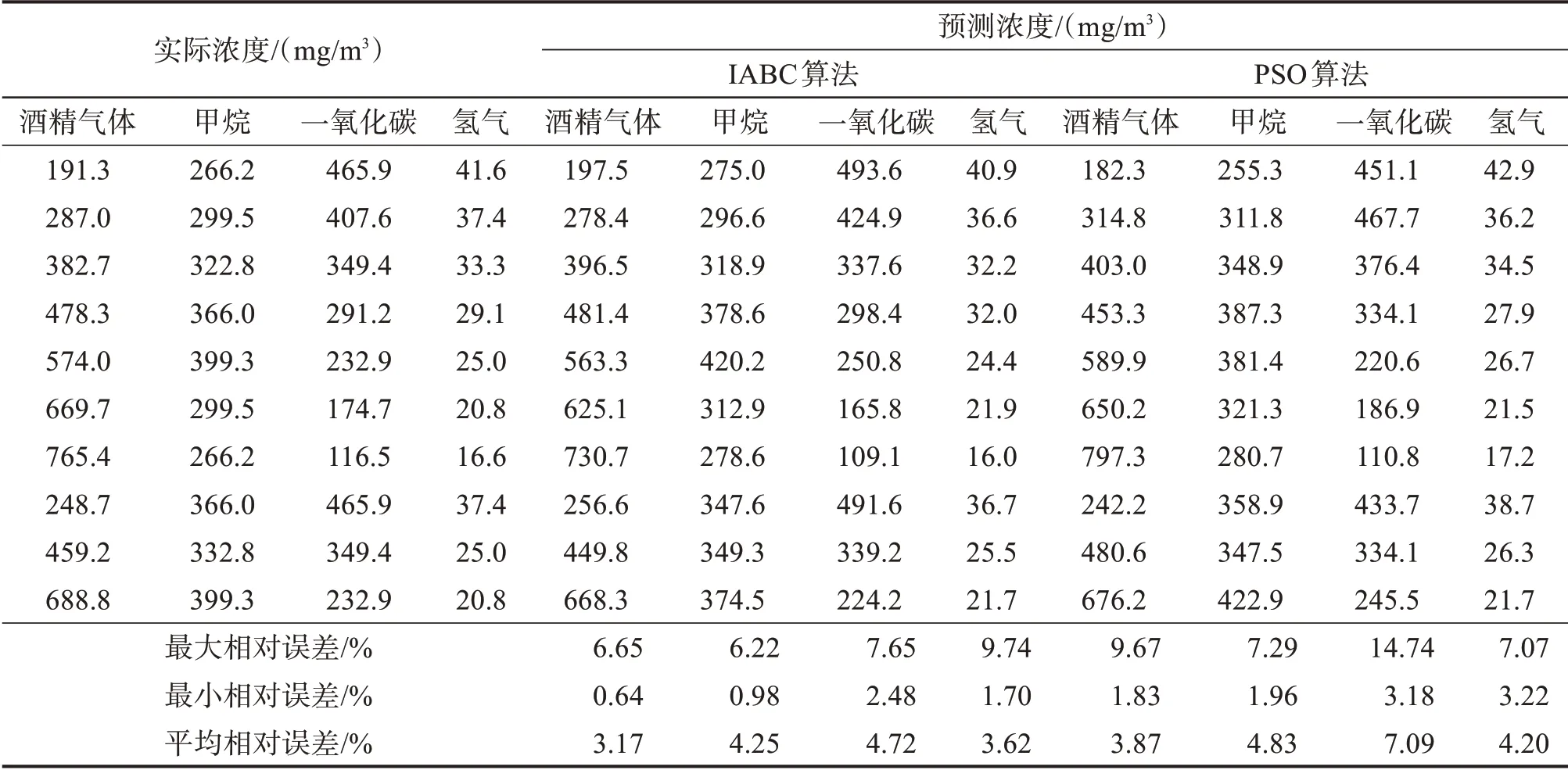
表5 基于IABC-LSSVM和PSO-LSSVM的混合氣體各組分濃度測試結果Table 5 Test results of concentration of each component of mixture gas based on IABC-LSSVM and PSO-LSSVM

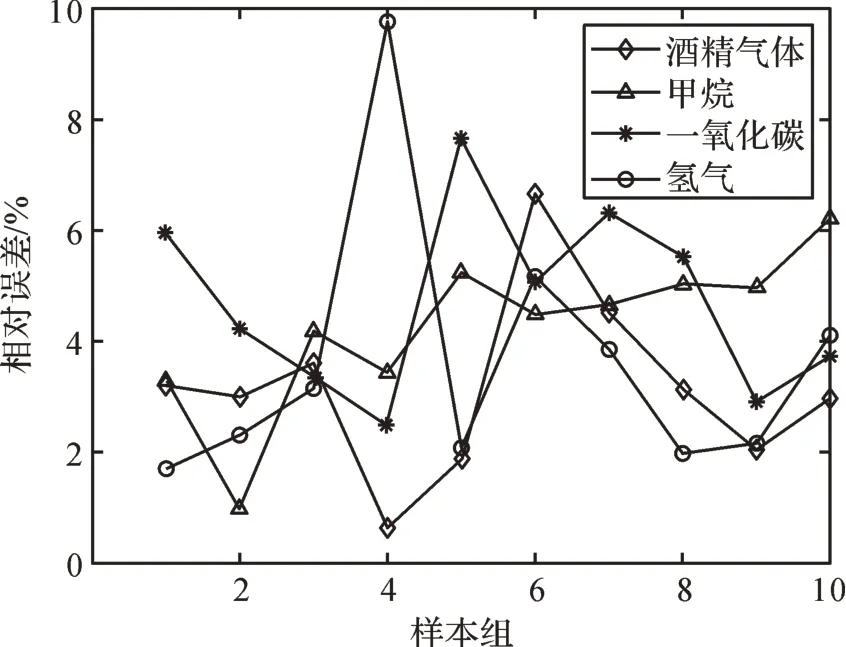
圖8 基于IABC-LSSVM 的混合氣體各組分濃度預測的相對誤差Fig. 8 Relative error of concentration prediction of each component of mixture gas based on IABC-LSSVM

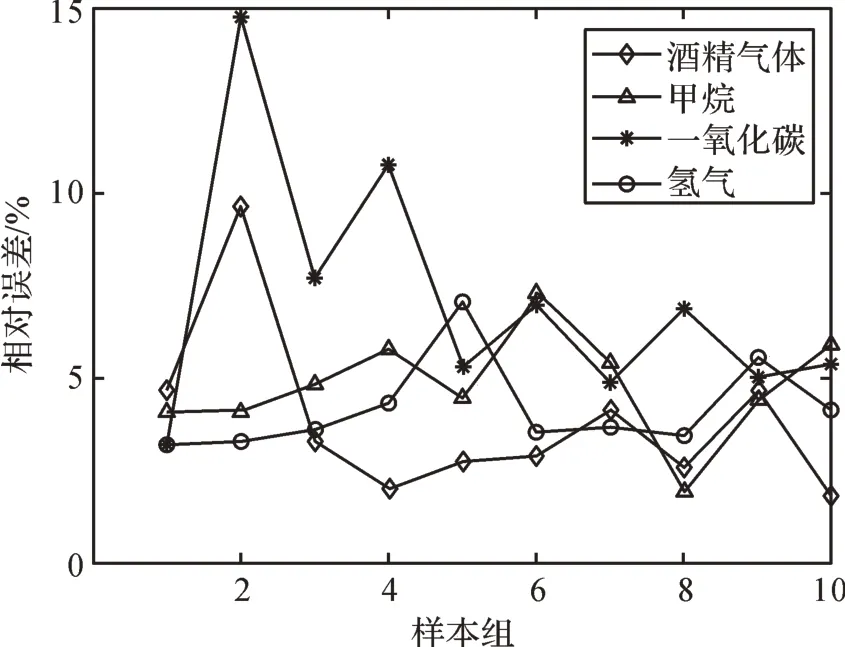
圖9 基于PSO-LSSVM 的混合氣體各組分濃度預測的相對誤差Fig. 9 Relative error of concentration prediction of each component of mixture gas based on PSO-LSSVM

通過表5、圖8、圖9可以看出，基于IABC算法和PSO算法所建立的定量分析模型對混合氣體各組分濃度的預測誤差水平是不同的。采用IABC 算法優化LSSVM 后對各組分氣體濃度預測的平均相對誤差分別為3.17%（酒精氣體）、4.25%（甲烷）、4.72%（一氧化碳）、3.62%（氫氣），低于PSO 算法優化LSSVM后預測的平均相對誤差（3.87%（酒精氣體）、4.83%（甲烷）、7.09%（一氧化碳）、4.20%（氫氣））。結果表明IABC算法優化的LSSVM在交叉敏感狀態下對混合氣體各組分濃度的預測精度要優于PSO算法優化的LSSVM，且IABC 算法比PSO 算法具有更強的魯棒性。

4 結 論

本文提出了一種利用IABC 優化LSSVM 的方法，并將它應用于交叉敏感狀態下混合氣體的定量分析。通過在標準ABC算法中引入自適應遞減因子，并結合輪盤賭和反向輪盤賭選擇機制來改進待工蜂跟隨概率公式，提高了算法的收斂精度。利用IABC算法優化LSSVM的參數，并使用優化后的參數重建定量分析模型，以提高對混合氣體各組分濃度的測量精度。

通過5 個常用的基準測試函數對IABC 算法和PSO算法進行測試后表明，IABC算法具有更高的收斂精度。混合氣體定量分析實驗表明，采用IABC算法對各組分氣體定量分析模型進行優化，優化所用的總時間和各模型的均方誤差均低于采用PSO 算法的；利用優化后的各組分氣體定量分析模型對混合氣體各組分濃度進行預測，IABC-LSSVM 對混合氣體各組分濃度預測的平均相對誤差也低于PSO-LSS-VM。因此，在交叉敏感狀態下，利用IABC算法優化LSSVM 的方法可有效提高混合氣體各組分濃度的測量精度。