萊洛三角形微孔織構化端面密封性能數值模擬

章亦聰，朱 瑋，吳玉國，時禮平,2

（1. 安徽工業大學機械工程學院，安徽馬鞍山243032；

2. 特殊服役環境的智能裝備制造國際科技合作基地，安徽馬鞍山243032）

機械密封是保障旋轉設備減少泄漏、穩定運行的重要裝置［1］。在流體機械的維護中，尤其在機器啟動和停車的過程中，經常出現因摩擦加劇而導致密封端面剛度不足、泄漏率過大和穩定性降低等問題，從而使密封系統失效。在密封端面設置具有一定結構及排布方式的微孔表面織構，通過流體介質的動壓效應在密封動、靜環間形成一層薄膜，實現非接觸式密封，可有效減少摩擦副之間的摩擦磨損，提高流體潤滑性能［2-4］。

國內外研究表明，密封端面表面織構形狀對流體潤滑特性具有一定影響［5-6］。李俊玲等［7］提出了一種非規則對稱葫蘆形表面織構，并研究了正方向葫蘆形表面織構的流體動壓效應和摩擦系數。Adjemout等［8］利用流體動力學模型與質量守恒空化模型相結合的方法，研究了三角形微孔形狀和排布形式對機械密封性能的影響。Blasiak 等［9］選取圓錐面、螺旋槽面、波紋面和徑向槽面四種形狀的密封端面，利用數值方法求解了采用不同密封端面時流體的非線性雷諾方程和靜環的運動方程，并分析了不同工作參數和幾何參數對流體潤滑性能的影響。Galda 等［10］研究了球狀微孔織構化密封端面的摩擦磨損特性，并與無表面織構密封端面的潤滑特性進行比較。Wang等［11］采用一種多目標優化的方法改進了具有自由邊的微孔形狀，并得出不對稱“V”型槽織構化密封端面具有更好的承載能力和泄漏率。Imai等［12］從理論和實驗兩方面研究了縱向、橫向和人字型微槽織構化密封端面的摩擦特性，發現人字型微槽織構化密封端面的摩擦系數最低。

對于不同形狀的密封端面表面織構，三角形與圓形微孔表面織構的研究居多。李茂元等［13］研究了三角形微孔的面積率、偏轉角度和偏轉方向對無量綱平均壓力的影響，并獲得了三角形微孔織構化密封端面的壓力分布。阮鴻雁等［14］建立了三角形與多圓弧復合織構化密封端面的幾何模型，并利用Fluent軟件分析了流體動壓潤滑性能。張穎等［15］建立了九圓微孔織構化密封端面模型，并與單微孔織構化密封端面模型進行對比，得出了圓形微孔織構表面協同作用的機理。楊笑等［16］利用有限單元法分析了圓形、三角形和方形微孔織構化密封端面在穩態條件下的液膜壓力、膜厚和溫度等參數以及密封性能參數。Yu等［17］利用超松弛迭代算法研究了三角形、圓形和橢圓形微孔織構化密封端面的流體動壓潤滑性能，并對比了它們的油膜開啟力和泄漏率。佘寶瑛等［18］利用JFO（Jakobsson-Floberg-Olsson）空化算法分析了不同幾何參數和操作參數下不同形狀微孔織構化密封端面的油膜壓力分布和密封性能。

綜上所述，表面織構的輪廓形狀是影響密封端面性能的重要因素。具體而言，三角形、正方形、菱形等微孔織構具有直線輪廓特征，圓、橢圓等微孔織構則具有曲線輪廓特征，這2種典型的輪廓特征微孔形狀組合后的復合微孔織構化密封端面的性能尚不明確。因此，筆者提出一種融合直線、曲線輪廓特征的萊洛三角形新型微孔織構，借助數值模擬的方法來考察萊洛三角形織構化端面的密封性能，并與圓形、三角形微孔織構化密封端面的密封性能進行比較，旨在為機械密封端面的表面織構創新設計提供新的思路。

1 微孔織構化密封端面數學模型

1.1 幾何建模

機械密封端面的密封環由相對旋轉的動、靜環組成。鑒于密封端面的周期對稱性，為了提高運算效率，在密封動環表面中心設置周期數N=36。織構面積率（織構端面面積與動環端面面積之比）Sp相同且沿周向均勻分布的圓形、三角形、萊洛三角形微孔織構如圖1所示。

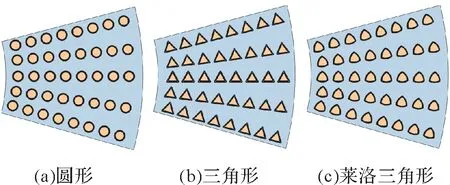
圖1 動環表面不同形狀的微孔織構Fig. 1 Micro-dimpled textures with different shapes on the rotating ring surface

機械密封端面的密封環截面如圖2所示，其中：密封間隙為hp，孔深為hd，密封環內、外徑分別為rin、rout；動環沿順時針方向旋轉，轉速為n，靜環靜止不動，動、靜環端面保持相對平行。

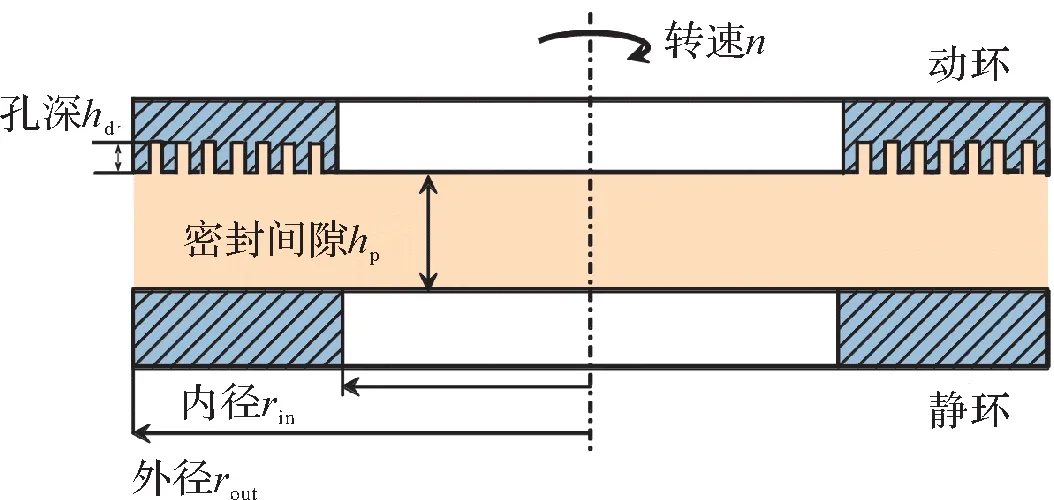
圖2 機械密封端面的密封環截面示意圖Fig. 2 Schematic diagram of sealing ring section of mechanical sealing end face

沿徑向取一個單元體為研究對象，建立圓形、三角形、萊洛三角形微孔織構化密封端面的數學模型，研究密封端面流體的壓力分布，分析3種不同形狀微孔織構化密封端面的織構面積率、孔深，以及密封間隙、操作壓力和轉速對密封端面性能的影響，并分別探究開啟力F和泄漏率Q的變化規律，構造開漏比I=F/Q，開漏比越大表示在泄漏率相同的情況下密封端面的開啟力越大。

利用GAMBIT軟件對3種形狀微孔織構化密封端面模型進行網格劃分：將與流體接觸的動、靜環兩端面指定為源面，選擇Copper類型對單元體進行劃分。沿密封環軸向進行端面網格節點映射，結果如圖3 所示。單元體外徑面和內徑面分別為壓力入口和壓力出口，與動環和靜環接觸的面分別為動壁面和靜壁面，取壓力進出口的平均壓力作為定值參數，兩側面為周期性邊界條件。為求解連續介質方程，需假定流體介質的密度與黏度均保持不變，流場的溫度不變，流體為不可壓縮的牛頓流體。利用Fluent軟件定常流動的穩態求解器計算流場并得到密封端面的開啟力和泄漏率。為加速迭代收斂過程，選擇可修正壓力系數的SIMPLIC 算法求解速度場和壓力場，并采用二階迎風格式的離散方法對控制方程在網格節點進行離散。

1.2 數值求解

在流體動壓潤滑的條件下，假定流體介質為全膜潤滑下的不可壓縮牛頓流體，忽略流體慣性力與體積力；假定流體運動為層流流動，無湍流和紊流現象，不考慮溫度和表面變形的影響；沿膜厚方向的壓力保持不變，忽略表面的粗糙度，在Fluent軟件中依據簡化的雷諾方程進行數值求解。簡化的雷諾方程為：

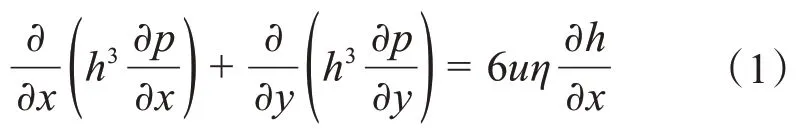
式中：x、y 分別為直角坐標系下的橫、縱坐標；h 為流體的局部膜厚；p為流體的壓力分布；u為兩表面間的相對速度；η為流體的動力黏度。

流體的局部膜厚為：

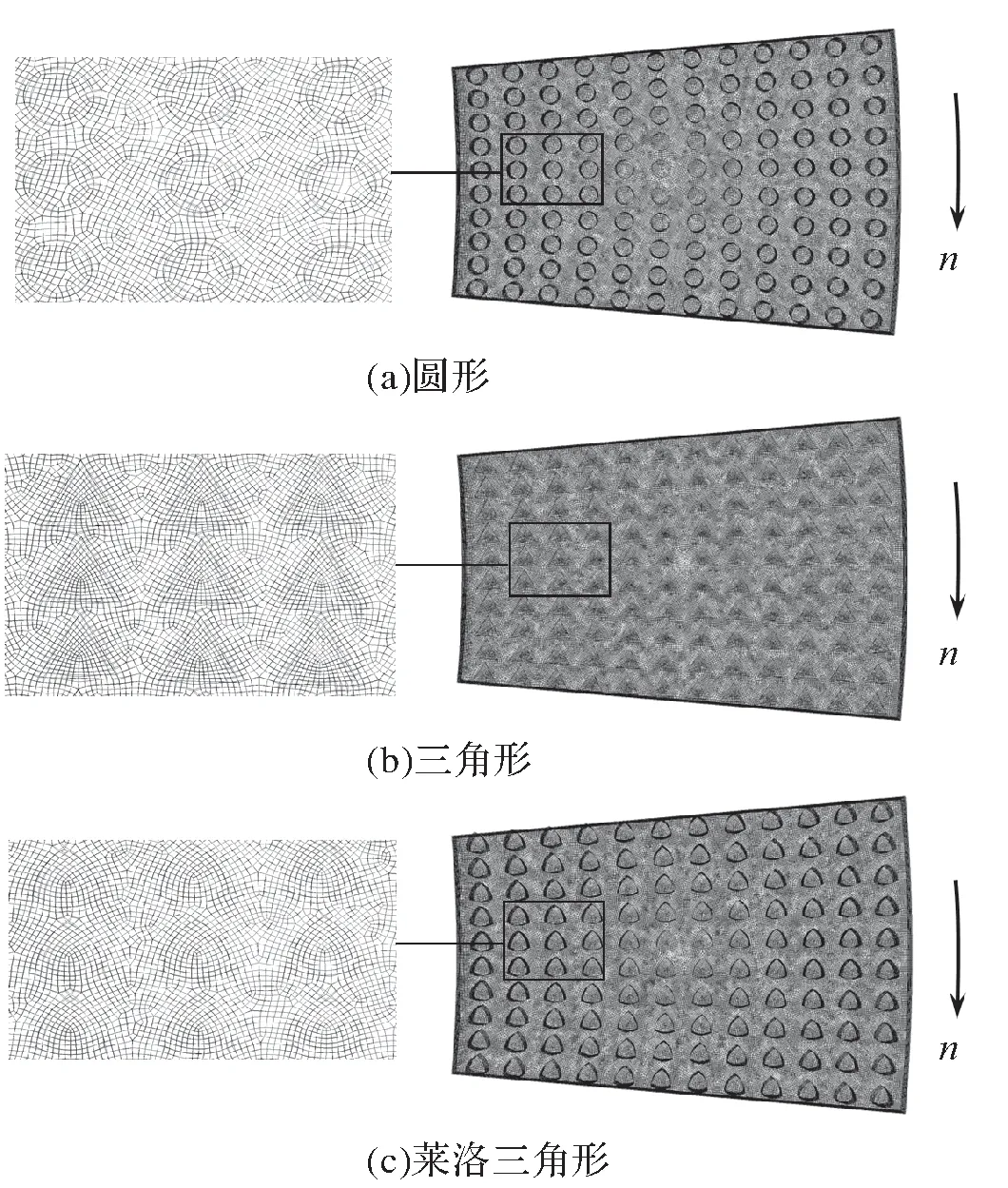
圖3 微孔織構化密封端面模型網格節點映射Fig. 3 Node mapping of micro-dimpled textured sealing end face model mesh

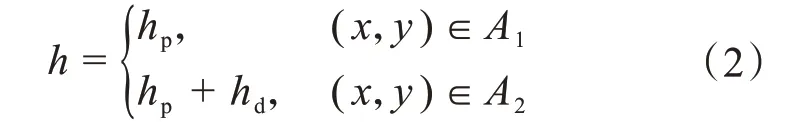
式中：A1、A2分別表示無孔區域和有孔區域。

通過求解耦合方程（1）、（2）可以得到液膜的壓力分布。在計算區域邊界處給出環境壓力定義域作為邊界條件，滿足的強制性邊界條件為：

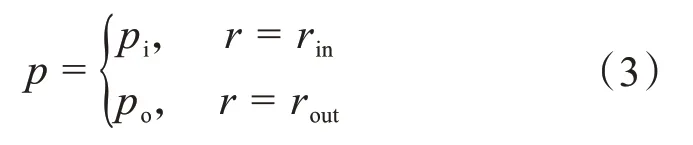
式中：pi、po分別為密封環內外徑面的入口壓力和出口壓力；r為流體質點到環心的局部半徑。

滿足的周期性邊界條件為：

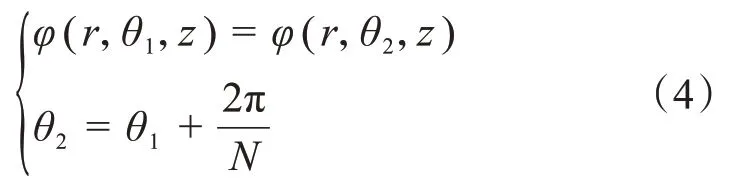
式中：θ1、θ2分別為一個單元體端面沿圓周方向的起、止角度；z為直角坐標系下的豎坐標。

為減少空化效應對流體的影響，可選擇空化條件影響較小的密封端面徑向非開口區域用于計算開啟力F和泄漏率Q，滿足：

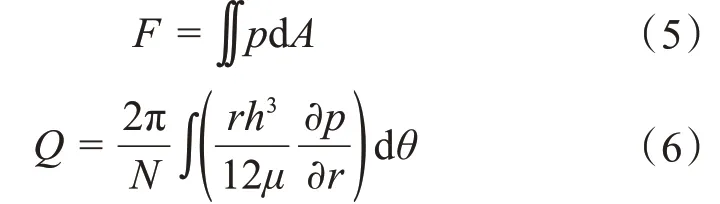
式中：dA 為密封端面單元體微元面積；μ 為流體在

25℃下的運動黏度；θ 為一個單元體所對應的圓周角度。

2 微孔織構化密封端面性能分析

2.1 密封端面壓力分布

密封環內徑rin＝15 mm，外徑rout＝20 mm，密封間隙hp＝1～8 μm，孔深hd＝1～8 μm，織構面積率Sp＝10%～50%，轉速n＝1 000～10 000 r · min-1；設置流體為清水，其密度ρ＝998.2 kg · m-3，動力黏度η＝0.001 003 kg ·( m · s)-1，溫度為25 ℃。圖4 為在hp＝2 μm，hd＝2 μm，Sp＝10%，n＝8 000 r · min-1，pi＝0.2 MPa，po＝0.1 MPa 條件下3 種微孔織構化密封端面的流體壓力分布。由圖4可知，流體壓力沿圓周方向周期性均勻分布，沿徑向方向從外向內逐漸減小。密封環外徑處線速度大，因此外側流體可獲得較大的動能和壓力。

單個圓形、三角形、萊洛三角形處微孔織構化密封端面的流體壓力分布如圖5所示，其中3種密封端面的單元面積、孔深和密封間隙均相同。由圖5 可知，密封端面的壓力沿速度方向收斂，在流體域孔壁碰撞處，由于壁面的阻擋，動能瞬間轉化為壓力勢能而使壓力快速增大，導致發散區域液體膜產生附加的承載能力，一部分流體回流使得局部旋渦處流體壓力抵消，在流體進入微孔處形成負壓。

2.2 織構面積率Sp對密封性能的影響

在n＝8 000 r · min-1，hd＝2 μm，hp＝2 μm，pi＝0.2 MPa，po＝0.1 MPa條件下，密封性能參數隨織構面積率的變化曲線如圖6所示。由圖6（a）可知：3種微孔織構化密封端面的開啟力均呈先減小后增大的變化規律，當Sp≈15% 時開啟力最大；同一Sp下，萊洛三角形微孔織構化密封端面的開啟力最大，三角形微孔織構化密封端面的開啟力最小。由圖6（b）可知：3種微孔織構化密封端面泄漏率的變化規律十分接近，均隨織構面積率的增大而增大，增速先逐漸增大后趨于平緩；同一Sp下，泄漏率從大到小依次為三角形微孔織構化密封端面、圓形微孔織構化密封端面、萊洛三角形微孔織構化密封端面。由圖6（c）可知：隨著Sp的增大，3種微孔織構化密封端面的開漏比均先增大后減小，當Sp≈10%時，開漏比均達到最大值；同一Sp下，開漏比由大到小依次為萊洛三角形微孔織構化密封端面、圓形微孔織構化密封端面、三角形微孔織構化密封端面。綜上可知，當Sp＜50%時，在相同的條件下，萊洛三角形微孔織構化端面的密封性能最好。

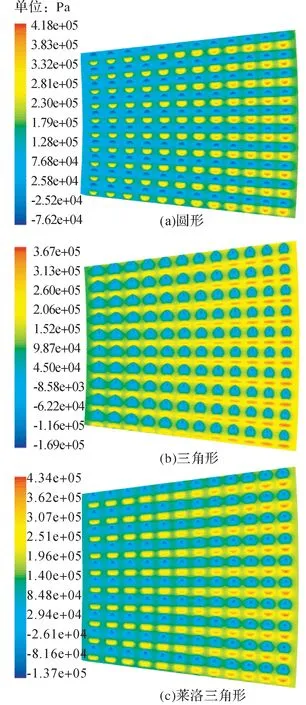
圖4 3種微孔織構化密封端面的流體壓力分布Fig. 4 Fluid pressure distribution of three kinds of micro-dimpled textured sealing end face

2.3 孔深hd對密封性能的影響

在n＝8 000 r · min-1，hp＝2 μm，pi＝0.2 MPa，po＝0.1 MPa，Sp＝10% 條件下，密封性能參數隨孔深的變化曲線如圖7 所示。由圖7（a）、7（b）可知：隨著hd的增大，3種微孔織構化密封端面的開啟力和泄漏率均先增大后減小；當hd＝2 μm時，開啟力均達到最大；當hd＝3～4 μm時，泄漏率均為最大。通過對比可知，在相同的hd下，萊洛三角形微孔織構化密封端面可獲得最大的開啟力和最小的泄漏率，而三角形微孔織構化密封端面的泄漏率最大且開啟力最小。由圖7（c）可知：3種微孔織構化密封端面的開漏比變化均十分明顯，隨著hd的增大，開漏比均先增大后減小；同一hd下，開漏比由大到小依次為萊洛三角形微孔織構化密封端面、圓形微孔織構化密封端面、三角形微孔織構化密封端面。這表明在其他條件相同時，萊洛三角形微孔織構化密封端面具有最優的動壓效應和密封性能。

圖5 單個微孔處織構化密封端面的流體壓力分布Fig. 5 Fluid pressure distribution of single micro-dimpled textured sealing end face

2.4 密封間隙hp對密封性能的影響

在n＝5 000 r · min-1，hd＝3 μm，pi＝0.2 MPa，po＝0.1 MPa，Sp＝10% 條件下，密封性能參數隨密封間隙的變化曲線如圖8所示。由圖8（a）、8（b）可知：3種微孔織構化密封端面的開啟力和泄漏率十分接近；隨著hp的增大，開啟力近似呈反比例函數規律逐漸減小，當hp＜3 μm 時，開啟力均較大；隨著hp的增大，泄漏率均近似呈二次函數規律逐漸增大，當hp＞6 μm后，泄漏率均急劇增大。由圖8（c）可知：3 種微孔織構化密封端面的開漏比變化曲線十分接近；隨著hp的增大，開漏比均先急劇減小后趨于平緩；同一hp下，萊洛三角形微孔織構化密封端面的開漏比略微大于圓形和三角形微孔織構化密封端面。當hp＜3 μm 時，3種微孔織構化密封端面均具有明顯的動壓效應和良好的密封性能。

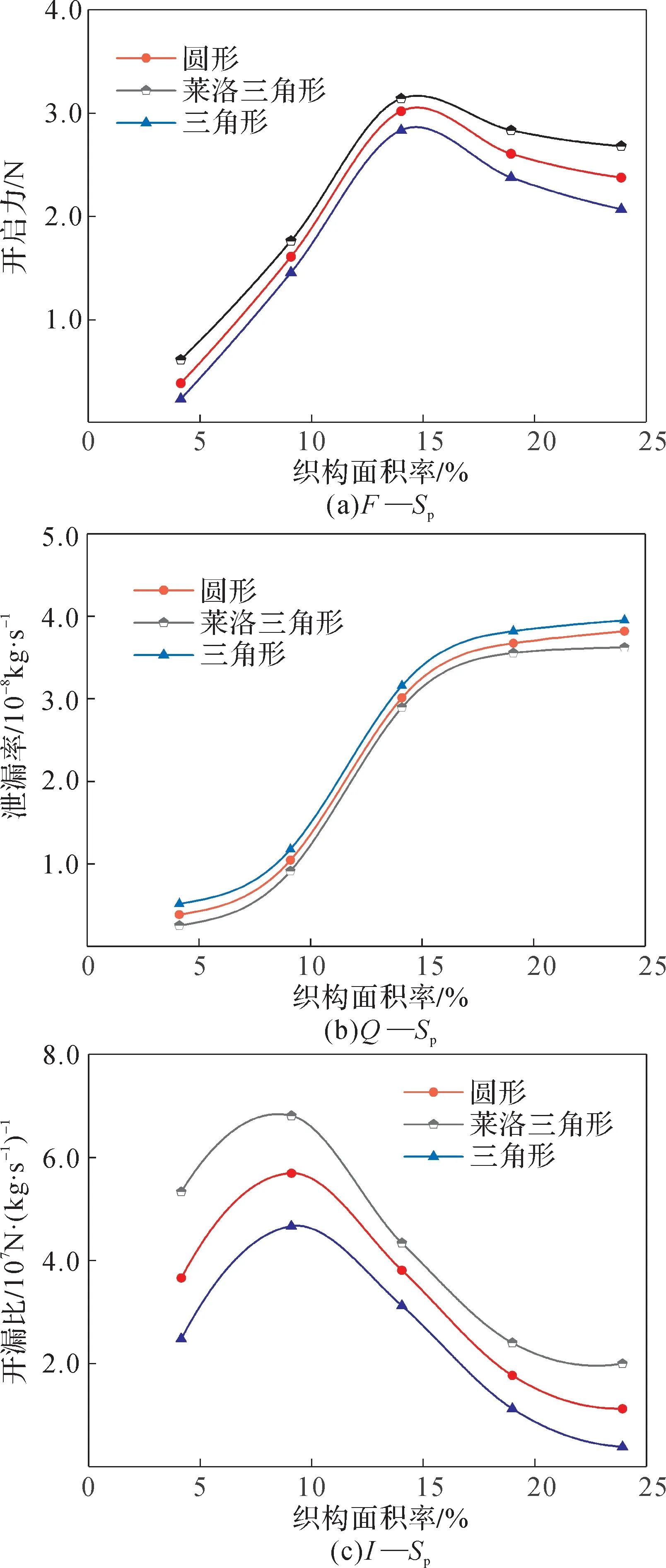
圖6 密封性能參數隨織構面積率的變化曲線Fig. 6 Variation curve of sealing performance parameters with texture area ratio

2.5 操作壓力pi對密封性能的影響

操作壓力為微孔織構化密封端面在理想環境下的平均壓力，通常以密封環的入口壓力pi作為操作壓力。

在Sp＝20%，hp＝3 μm，hd＝4 μm，n＝8 000 r/min，po＝0.1 MPa，θ＝225°條件下，密封性能參數隨操作壓力的變化曲線如圖9所示。由圖9（a）可知：隨著pi的增大，3種微孔織構化密封端面的開啟力均逐漸增大；同一pi下，萊洛三角形微孔織構化密封端面的開啟力最大，其次為圓形微孔織構化密封端面，三角形微孔織構化密封端面的最小。由圖9（b）可知：3種織構化密封端面的泄漏率隨著pi的增大近乎直線上升，且同一pi下泄漏率相差不大。由圖9（c）可知：3種微孔織構化密封端面的開漏比均隨著pi的增大先急劇減小，后逐漸趨于平穩；當pi＜0.3 MPa時，由于密封端面的泄漏率比較小，因此其開漏比比較大；當pi＞0.3 MPa時，3種微孔織構化密封端面的開漏比十分接近。

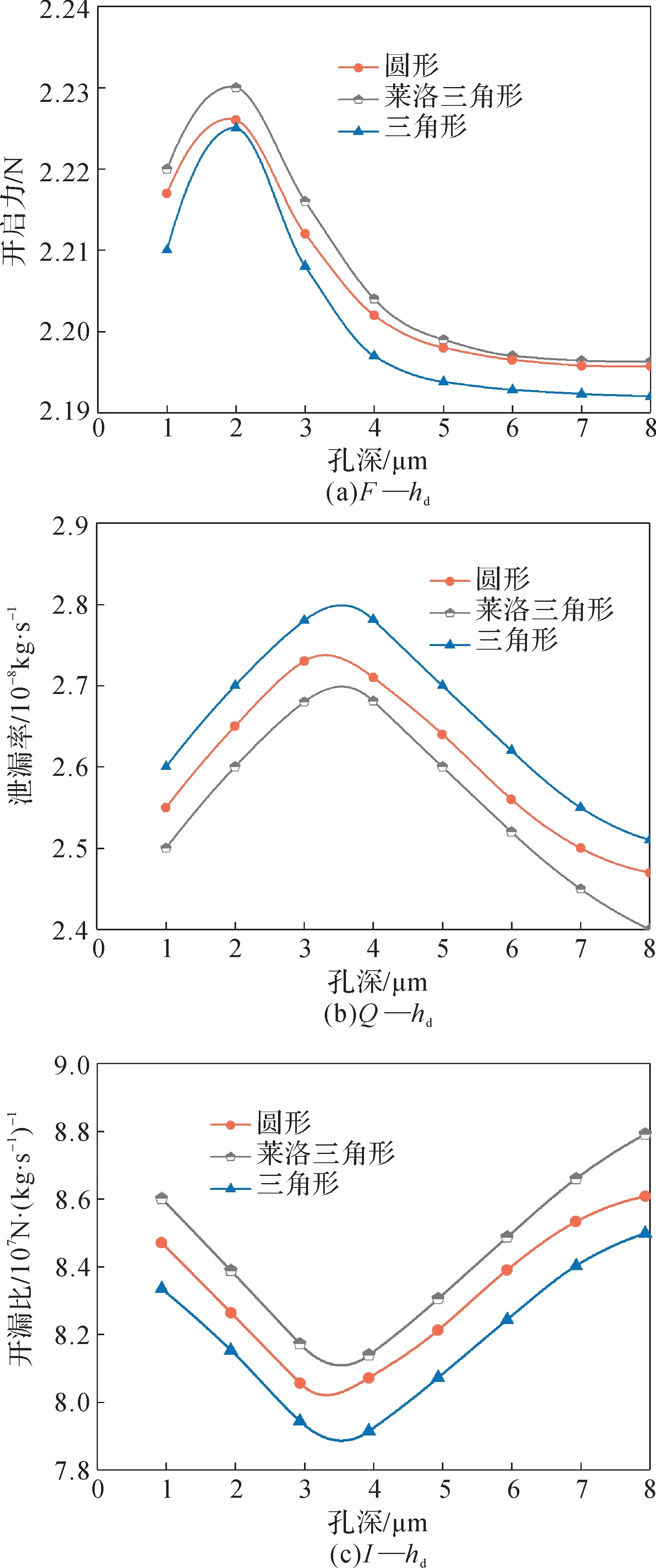
圖7 密封性能參數隨孔深的變化曲線Fig. 7 Variation curve of sealing performance parameters with hole depth

2.6 轉速n對密封性能的影響

圖8 密封性能參數隨密封間隙的變化曲線Fig. 8 Variation curve of sealing performance parameters with seal gap

在Sp＝20%，hp＝3 μm，pi＝0.2 MPa，po＝0.1 MPa，hd＝4 μm 條件下，密封性能參數隨轉速的變化曲線如圖10所示。由圖10（a）、10（b）可知：隨著n的增大，流體的動壓效應增強，3 種微孔織構化密封端面的開啟力和泄漏率均呈現線性增大的變化規律；同一n下，萊洛三角形微孔織構化密封端面具有最大的開啟力和最小的泄漏率，三角形微孔織構化密封端面的泄漏率最大而開啟力最小。由圖10（c）可知：3 種微孔織構化密封端面的開漏比均隨n的增大而逐漸增大；同一n下，開漏比從大到小依次為萊洛三角形微孔織構化密封端面、圓形微孔織構化密封端面、三角形微孔織構化密封端面。

2.7 密封性能影響的原因分析

綜上所述，在孔深、密封間隙相同的條件下，萊洛三角形微孔織構化密封端面具有最大的開啟力、最小的泄漏率和最大開漏比，這可能是因為萊洛三角形具有直線和曲線兩種輪廓特征，在直線邊緣產生較強的動壓效應的同時，平滑的弧邊能夠減小流體流動時發生的速度突變，使得流體流過織構表面時能充分進入微孔，進而減小了密封端面的泄漏率。

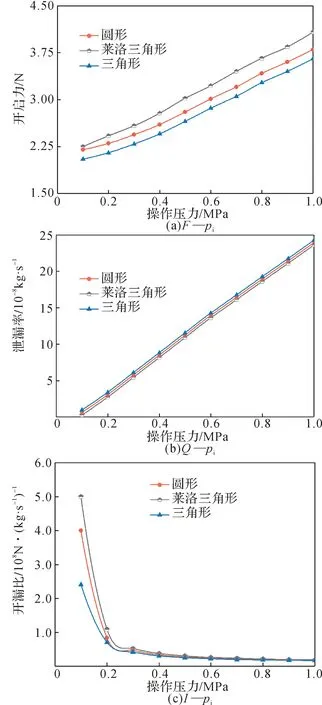
圖9 密封性能參數隨操作壓力的變化曲線Fig. 9 Variation curve of sealing performance parameters with operating pressure

3 結 論

1）微孔織構化密封端面具有顯著的流體動壓效應，對于3種微孔織構化密封端面，其開啟力和泄漏率隨著織構面積率、孔深、密封間隙、操作壓力和轉速的增大均呈現相同的變化規律。

2）當Sp=10%，hd=3～4 μm，hp＜3 μm，pi＜0.3 MPa時，不同形狀的織構化密封端面均具有較好的密封性能；較小的幾何及工況參數有利于獲得較大的開漏比。

3）在相同的幾何參數和工況參數下，與圓形和三角形微孔織構化密封端面相比，萊洛三角形微孔織構化密封端面具有較大的開啟力和較小的泄漏率，同時具有較大的開漏比。

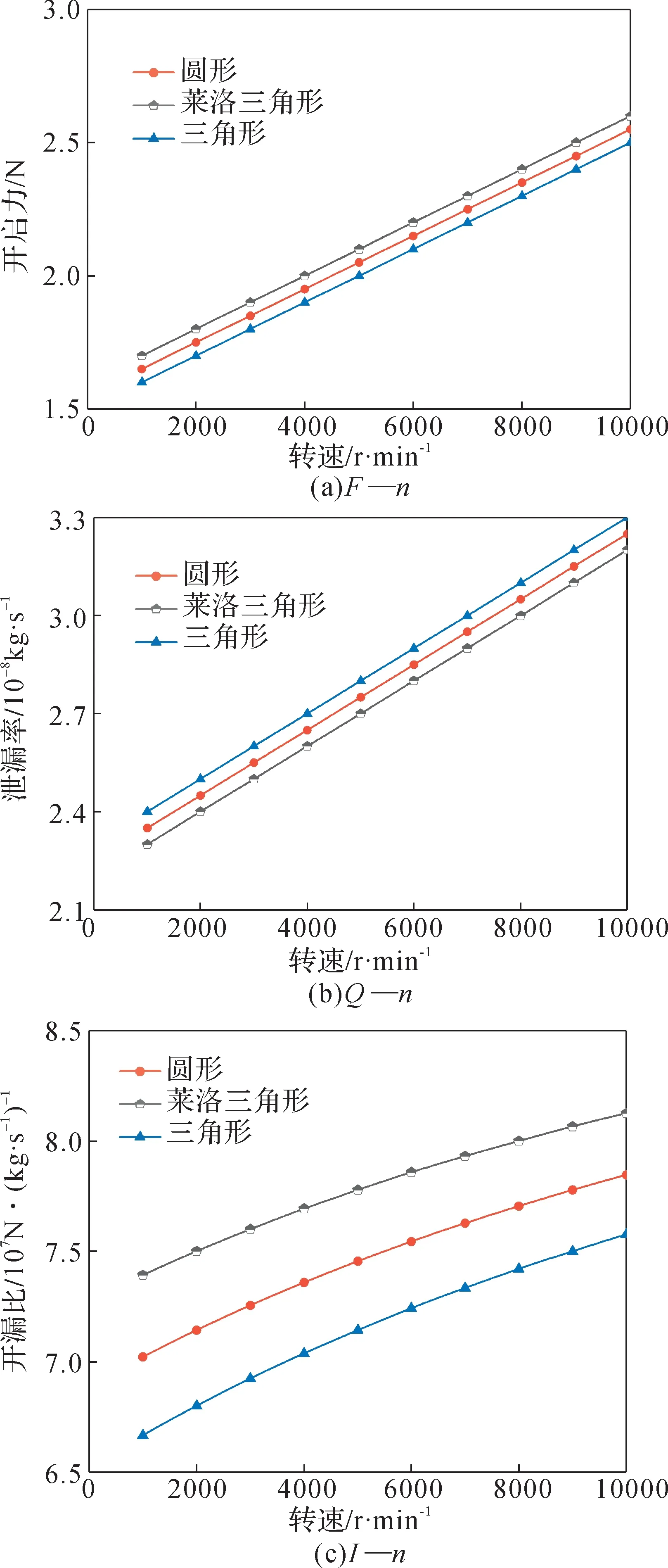
圖10 密封性能參數隨轉速的變化曲線Fig. 10 Variation curve of sealing performance parameters with rotational speed