基于DS理論的遙測定位數據有效性實時判別方法

馬方遠，杜劍英，申繼志，李鵬勃

(中國兵器工業試驗測試研究院，陜西 華陰 714200)

0 引言

現階段，在常規兵器靶場，使用遙測定位數據引導其他外測設備跟蹤測試已成常態，由于遙測數據的質量易受彈體姿態、空間電磁環境以及地形地貌變化的影響，遙測數據中往往有些誤碼，因此，使用遙測定位數據作為其他測試設備的引導源時，需要對遙測定位數據的有效性進行實時判斷[1-2]。

目前，遙測定位數據有效性實時判別的通常做法是直接使用包校驗技術[3]。對遙測定位數據所在的數據包進行包校驗檢查，包校驗檢查通過則認為遙測定位數據有效，否則無效。但由于遙測定位數據所在包的數據長度遠大于遙測定位數據的長度，直接使用包校驗技術判別遙測定位數據的有效性雖然可以濾除絕大多數的無效數據，但也會帶來兩個問題：一是過度濾除問題，即遙測定位數據有效，卻因其所在數據包其他數據誤碼導致包校驗失敗被濾除；二是濾除不干凈問題，即遙測定位數據無效，卻因包校驗規則漏洞包校驗通過而未被濾除。

DS證據理論[4-5]是在貝葉斯基礎上發展起來的，是對概率論的擴展，證據理論是處理集合的不確定問題，所以使用證據理論時，需將假設的命題與構建的集合之間建立一一對應關系，從而將命題的不確定問題轉換為集合的不確定問題來處理。DS理論引入了信任函數，因此可以將遙測定位信息的測試值與理論預測值的誤差用信任區間來描述，當誤差落在信任區間內時，判斷遙測定位數據有效[6]。

1 DS證據理論的基本概念

假設A和B是某一個集合里的兩個元素，若A∩B≠?(?表示空集)，就稱A和B是相容的，假設X的所有可能取值用一個集合U來表示，并且在U內的所有元素之間是互不相容的，就稱U是X的識別框架。設U為一個識別框架，函數m:2U→[0,1]并且在滿足下列條件時

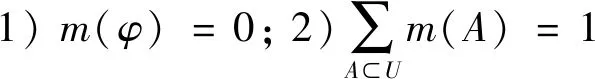
就稱m(A)是A的基本概率賦值，即對命題A的基本信任程度可以用m(A)表示。DS證據理論對于任一命題集合還提出了信任函數

A中每個子集的基本信任度之和就是A的信任函數，表示為BEL(A)，它可以表示對A的總信任度。假設把命題A當做識別框架U的一個元素，當m(A)>0時，就稱A是信任函數BEL的焦元。

2 遙測定位數據有效性判別方法

設x1(n),x2(n),x3(n)為n時刻飛行器的遙測定位數據中位置、速度、加速度的測試值；y1(n)，y2(n)，y3(n)為n時刻飛行器的理論彈道位置、速度、加速度的數值;z1(n),z2(n),z3(n)為n時刻飛行器的預測位置、速度、加速度值[7]。假設飛行器在時間段[n,n+1]內是勻加速運動，則飛行器的n時刻飛行器的預測位置、速度、加速度[8]可以表示為：

式中，當Δt為遙測定位數據的時間間隔，n=0表示起飛零點，則根據工程實踐得知，n≤0時，xi(n)，yi(n)，zi(n)(i=1，2，3)其值都為初始狀態值，且此時的值可以認為就是真值，即m(xi(n))，m(yi(n))，m(zi(n))在n≤0時其值都為1，m(A)為A的基本概率賦值。

當ai(n)?U時，則認為測試值不在合理的范圍內，此時的測試值是由遙測誤碼造成的，應當舍棄，在進行下一時刻預測時，測試值可以按下面公式進行取值：

在這里，位置信息x1(n)使用了x1(n-1)進行預估，而不像速度信息x2(n)與加速度信息x3(n)直接使用了理論值y2(n)，y3(n)代替，主要是考慮到彈箭實際飛行中，飛行軌跡與理論彈道可能有較大的差別，但是速度與加速度差別較小，為了減少迭代計算次數，方便計算效率。

因此，只要確定了一個識別框架U，使得測試值與理論值的誤差在識別框架內的概率賦值X合適，就可以使用上述方法對遙測定位數據的有效性進行判斷。當ai(n)?U時，可以判定此時刻測試值有效，當ai(n)?U， 判定此時刻測試值無效。

在實際工程中，識別框架U范圍以及概率賦值X的確定，可以通過實時動態的估計測試值與理論值的誤差范圍與概率[9]，具體實現方法如下：

1) 取一定長度N與一賦值概率X，統計遙測定位信息的測試值與預測值的誤差ai(n)，…,ai(n+N)的均方差σ；

2) 設bi=sσ,(s>0)，當滿足ai(n)在區間[0,bi]內的概率不小于給定的概率賦值X時，如果s≤3，則令s=3，則區間[0,bi]為判斷遙測定位數據有效性的識別框架。

值得注意的是，識別框架[0,bi]的最小上限為測試值與預測值均方差的3σ，是對有效數據的一種保護，即認為誤差在3σ以內都是有效數據。另外，X的取值越接近于1，本方法濾除無效遙測定位數據的能力越弱；X的取值過小，本方法將產生很多誤濾除，正常的遙測定位數據也很難通過有效性判別；N的取值越大，本方法濾除無效遙測定位數據的能力越強，但是延時輸出就越長。在實際工程應用中，X可取0.8～0.95之間，N可以根據遙測定位數據的周期，統籌均衡樣本量的數量與延時輸出，保證不影響需要引導跟蹤的設備跟蹤測試[10]。

3 試驗驗證

為了充分驗證算法的效率，本文的試驗驗證數據來自于某型號靶場試驗的遙測數據中導航計算機導航數據發射坐標系下的射程X，其數據周期為12 ms，最大射程為495 km，飛行過程386.64 s，共有3 223個點的數據，由圖1可以看出，且遙測數據的質量較差，誤碼較高。

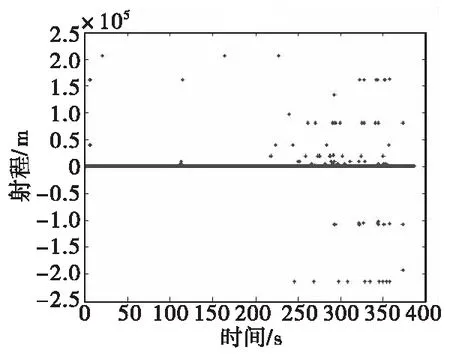
圖1 某試驗遙測數據中射程-時間數據曲線Fig.1 Range-time data curve in a test telemetry data

直接采用包校驗技術對遙測定位數據有效性進行判別(此數據的包校驗為8位校驗和)，判別結果如圖2所示。絕大部分的遙測誤碼已經濾除干凈，但仍有兩個無效遙測定位數據未被濾除，所剩共計2 988個有效數據。

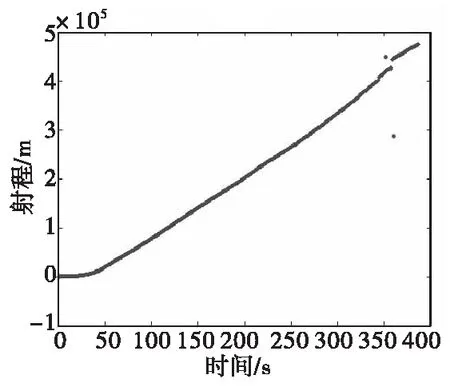
圖2 包校驗后剩余的數據曲線Fig.2 Data curve remaining after package verification

采用連續200個點(2.4 s延時輸出)的測試值與預測值進行動態誤差統計，統計并計算概率X為90%時的最小識別框架U的上下限。采用本文方法對下一個測試值進行有效性判斷，判斷結果如圖3所示。遙測誤碼造成的不正常數據已經濾除干凈，所剩共計3 029個點的有效數據，與圖2比較可以看出使用數據包包校驗技術，多濾除了41個有效遙測定位數據。

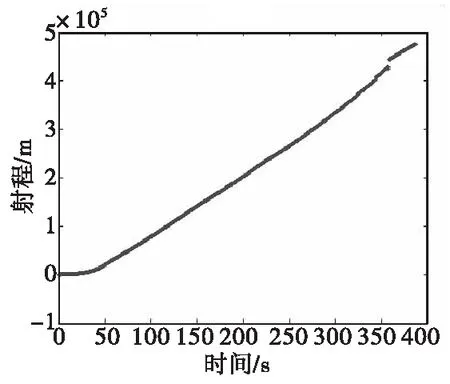
圖3 經過有效性判別后剩余數據曲線Fig.3 Residual data curve after validity discrimination

采用連續200個點(2.4 s延時輸出)的測試值與預測值進行動態誤差統計，統計并計算概率X為90%時的最小識別框架U的上下限。采用本文方法對下一個測試值進行有效性判斷，并使用預測值代替被剔除的無效遙測定位數據，補全引導數據后的數據如圖4。

圖4 補全后的引導數據Fig.4 Guidance data after completion

4 結論

本文提出了基于DS證據理論的遙測定位數據有效性實時判別方法，該方法利用了遙測數據中的定位數據的位置、速度、加速度信息和理論彈道位置、速度、加速度信息，預測遙測定位數據的合理范圍，使用DS證據理論原理，直接判斷遙測定位數據的有效性，因此避免了常規使用數據包包校驗技術帶來的遙測定位數據過度濾除問題。試驗驗證表明，基于DS證據理論的遙測定位數據有效性判別方法，可以更有效地濾除遙測定位數據中的無效數據。