多彈協同攔截制導律設計*

肖念遠，王曉芳，周 健

(1 北京理工大學宇航學院，北京 100081； 2 西安現代控制技術研究所，西安 710065)

0 引言

近年來，空戰武器和一體化防空系統飛速發展，戰場形式日益立體化、復雜化[1]。無人戰機作為重要軍事目標，配備多層次防御體系必要且緊迫[2]。傳統空中防御措施有被動防御(即機動躲避)、主動防御(即釋放紅外干擾彈等)[3]。防御彈機動性能和毀傷能力受限，僅靠單枚彈難攔截敵方襲擊，使得防御可靠性下降。

運用先進技術，無人戰機發射多枚防御彈主動防御，組成協同防御系統，能更有效的攔截[4]。設計滿足需求、適應戰場環境的協同攔截制導律，成了制導技術的研究熱點。協同攔截制導律的主要研究對象有我方目標(無人戰機)、一枚或多枚防御彈、敵方來襲彈。針對目標、來襲彈、防御彈的“三體”[5]問題，一般作為兩個并行制導問題，即來襲彈攻擊目標、防御彈攔截來襲彈[6-7]。文獻[8-9]研究了多枚導彈攔截來襲彈，但所需過載較大。一般情況下，來襲彈機動性能大于防御彈機動性能，存在脫靶量大，攔截失敗的可能。文獻[10-13]提出了不同種類的協同攔截制導律，但建立在線性化基礎上，需預估剩余飛行時間，且攔截的多為靜止目標，不滿足現代戰爭需求。

文中針對該情景，提供一種新的協同攔截思路。建立非線性運動方程組，基于極小值原理和動態逆理論設計兩種制導律，讓無人戰機順序發射兩枚防御彈，防御彈DA與無人戰機采用最優協同制導律OCGL，防御彈DB采用時間協同制導律TCGL，以減小防御彈DA的過載需求，實現兩枚防御彈同時攔截來襲彈，對防御彈發射間隔進行優化，使防御彈DB的攔截能量小且和DA打中M的攔截間隔相差小。

1 問題描述

假設來襲彈、目標(無人戰機)、防御彈在鉛垂面內運動，如圖1所示。

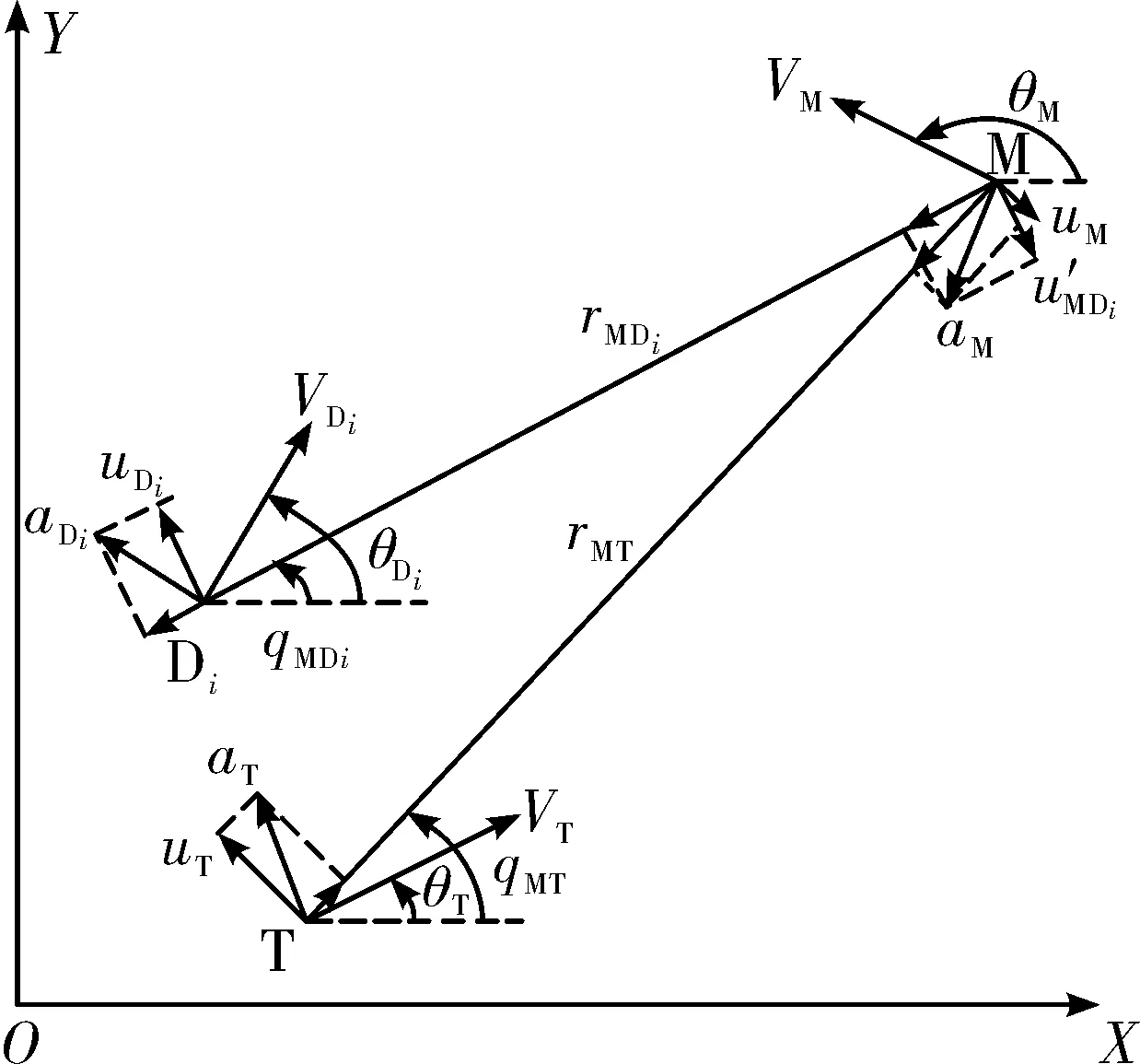
圖1 來襲彈-防御彈-目標相對運動示意圖

圖中，OXY為慣性坐標系，M、T、Di(i=A, B)分別為來襲彈、目標、目標發射的防御彈。Vj、aj、θj(j=M,T,Di)分別表示速度、垂直于速度矢量的加速度和彈道傾角。rMDi和rMT表示M與DA、DB、T之間的距離，qMDi和qMT為對應的視線角。uj為加速度矢量在垂直于視線方向的分量，u′MDi為M加速度在垂直于M-Di視線方向的分量。

M、Di和T的相對運動方程組為：

(1)

設M采用增強比例導引[14](APN)，則

(2)

式中，KM為M的制導系數。

2 協同攔截制導律設計

T順序發射DA和DB，T與DA以OCGL飛行，T協同，吸引M飛向DA，DA以小過載攔截M。基于動態逆理論[15-16]，令DB以TCGL飛行，DB-M彈目距離與DA-M趨于一致，與DA同時攔截M。

2.1 非線性OCGL設計

由式(1)可知DA與M相對運動方程組為:

(3)

對式(3)求導得:

(4)

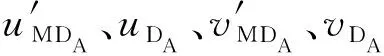
(5)

(6)

由圖1可知，u′M與uM之間的轉換關系為:

(7)

式(7)代入式(6)可得狀態方程為：

(8)

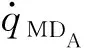
(9)

式(9)中，t1、tf為DA的發射和終止時刻，終端指標和動態指標的權重系數分別為a、b、c，有a≥0,b≥0,c≥0。

由性能函數和狀態方程得漢密爾頓方程：

(10)

式中，λ為協態量，正則方程和橫截條件為：

(11)

由極小值原理可知：

(12)

聯立可得最優控制的開環解為：

(13)

將式(13)代回狀態方程積分化簡可得：

(14)

將式(14)代入式(13)，得到采用OCGL的DA和T控制指令的閉環解。

2.2 多防御彈TCGL設計

T發射DA后，再發射DB，DB與DA同時命中M。基于動態逆理論，rMDB與rMDA趨于一致，可實現DA和DB的攔截時間協同。

定義彈目距離跟蹤誤差為：

(15)

對式(15)求導可得:

(16)

令實際速度前置角ηDB=qMDB-θDB。基于動態逆理論，設計期望速度前置角ηc為：

(17)

式中，Kr>0為衰減系數。當ηDB=ηc后，聯立式(16)和式(17)得，呈指數衰減，DB的彈目距離趨于實現時間協同。

令E=cosηc，反解ηc為：

(18)

式中：η0為DB的初始速度前置角；ηmax為DB的最大速度前置角。

由于ηDB=qMDB-θDB，求導可得：

(19)

基于動態逆理論設計θDB為：

(20)

式中Kη>0，為衰減系數。

為保證制導精確，考慮DB的導引頭識別距離、制導時間等因素的影響，令DB與M的彈目距離為Δr1時，轉入APN為：

(21)

式中，KDB為APN系數。

3 發射時間優化設計

受發射技術和戰場環境制約，DB無法與DA同時刻發射，假設T先發射DA，再發射DB。由于DB末制導轉APN，故DA、DB到達M的時間有誤差，通過文化算法計算兩枚防御彈發射間隔的最優解，使攔截間隔和DB能量小。

令DA發射時間為t1，DB發射時間為t2，發射間隔為Δt1=t2-t1，優化函數為:

(22)

式中:|Δt2|為DA和DB攔截M的時間差；為DB的控制能量；相應權重d>0，e>0。

設計變量Δt1的邊界約束條件為：

Xmax=Δt1，max，Xmin=Δt1，min

(23)

式中，Δt1，max和Δt1，min為DB發射時間上下限，由戰場形勢與技術能力決定，故優化模型的可行域為：

Ω=[Xmin,Xmax]

(24)

令過載需要滿足的過程約束為:

gj(X)=|nj|-njmax≤0,j=M,T,DA,DB

(25)

式中：nj為需用過載；njmax為可用過載。

綜上分析，發射間隔優化模型為：

(26)

優化模型建立之后，即用文化算法進行優化，得到Δt1的最優解，進而得到DB的發射時間t2=t1+Δt1。

4 仿真分析

4.1 OCGL仿真結果及分析

設t1=0，KM=4，a=1010,b=0.1,c=1。其余條件見表1，仿真結果如圖2～圖4所示。

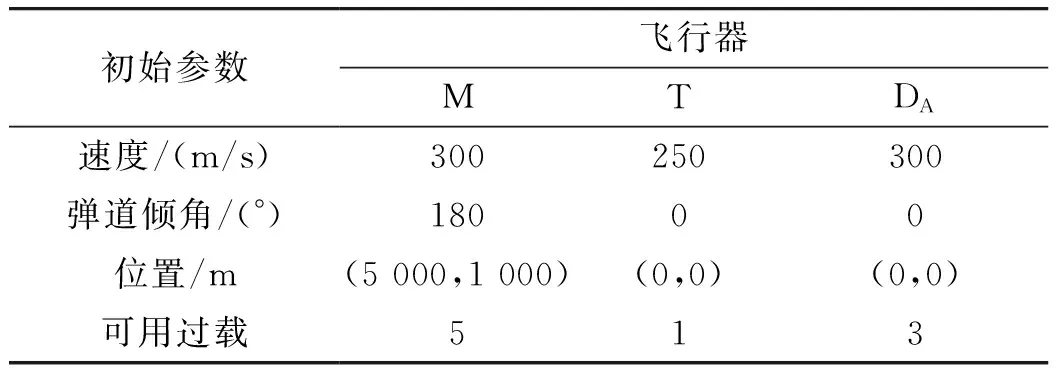
表1 OCGL仿真初始條件

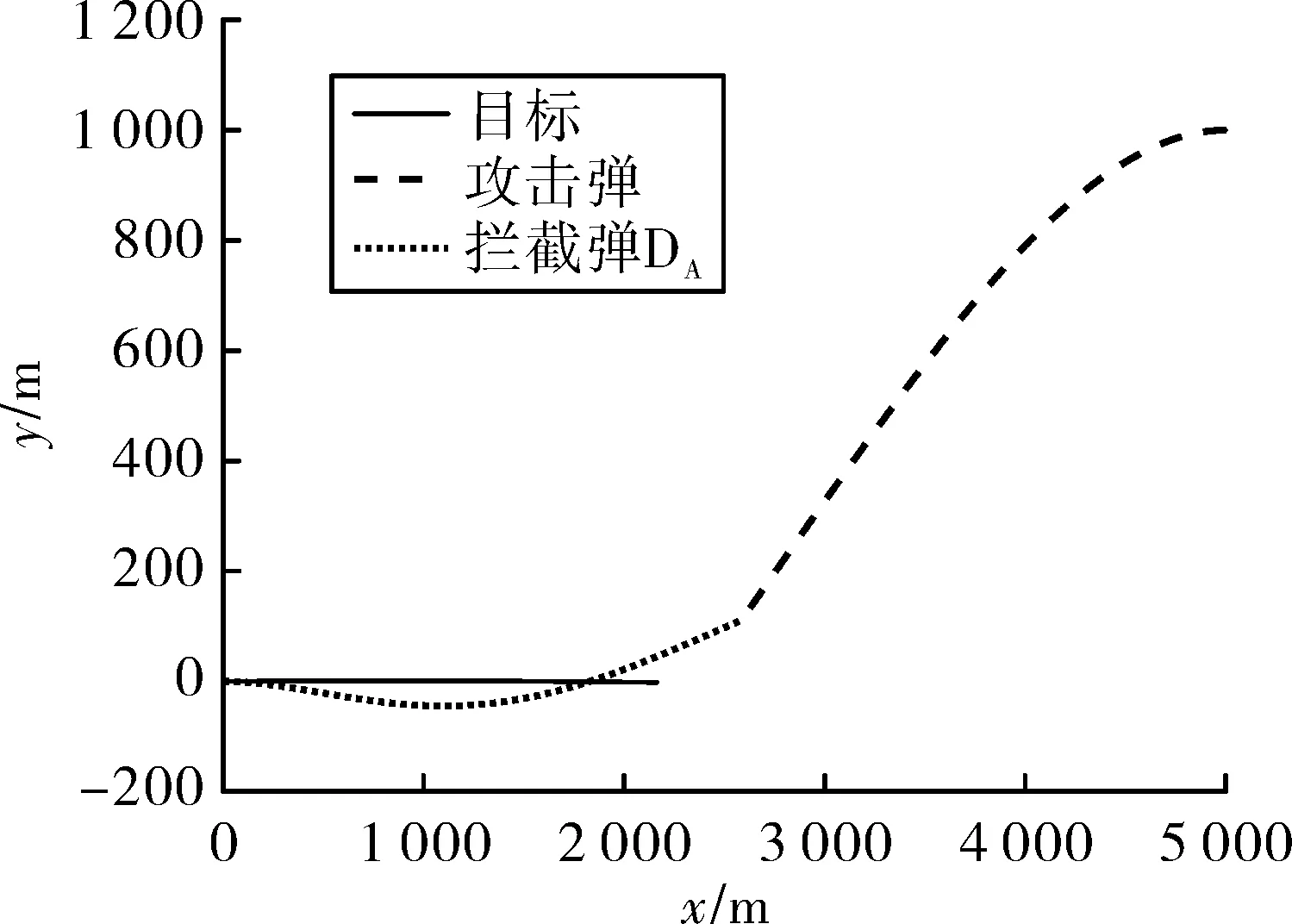
圖2 OCGL彈道圖

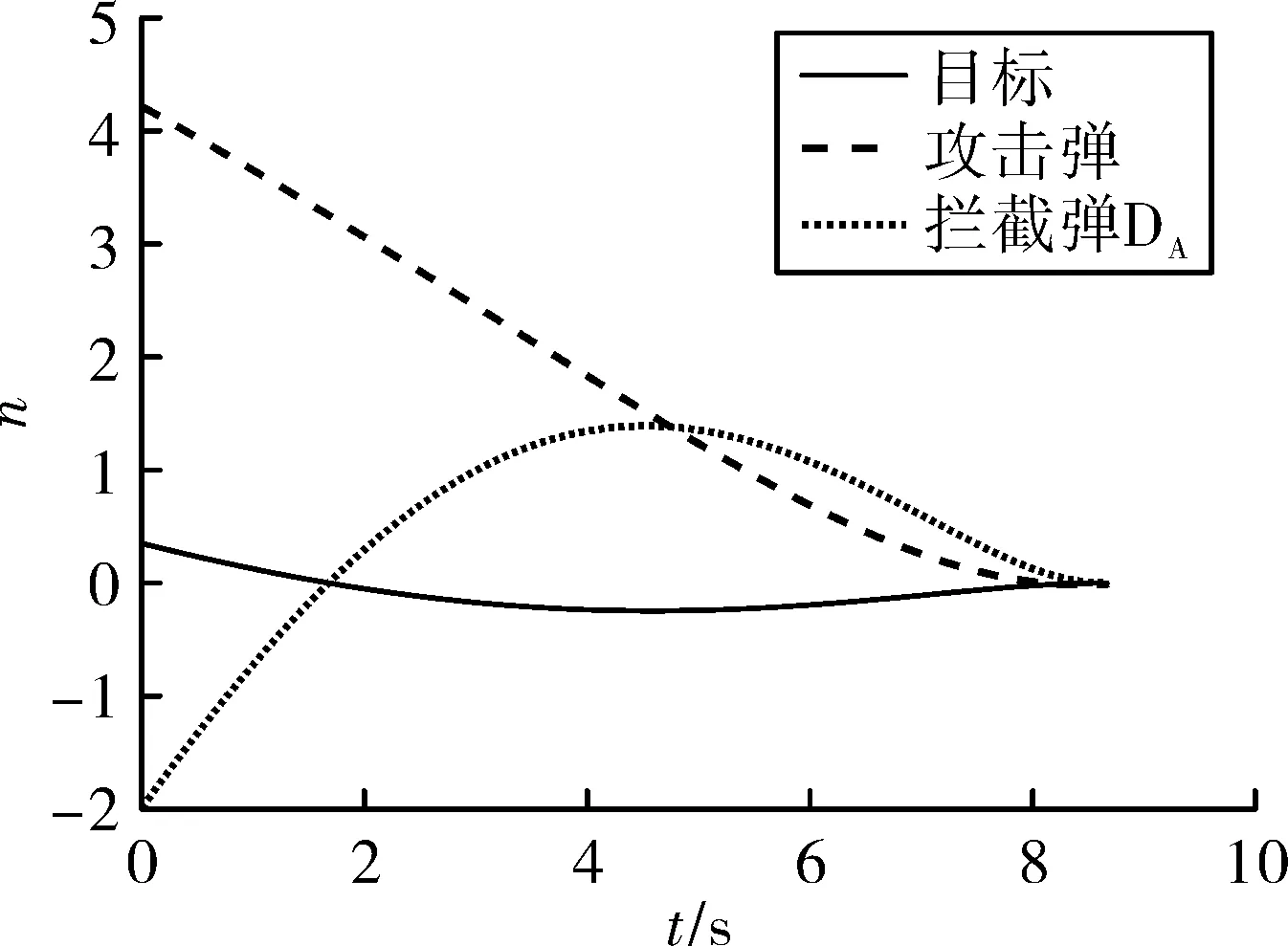
圖3 OCGL過載隨時間變化圖

圖4 OCGL視線角速度隨時間變化圖

由圖2知,在OCGL導引下，T向y軸負方向飛行，引誘M飛向DA。由圖3知，機動能力小的T和DA，成功攔截過載較大的M。圖4所示視線角速度均趨于零，表示OCGL實現對視線角速度的控制。該組結果證明OCGL可以實現低過載防御彈對高過載來襲彈的攔截。

4.2 TCGL仿真結果及分析

在表1的基礎上，令t2=0.5 s，VDB=320 m/s，KMDB=4，Kη=5，Kr=1，ηmax=30°，Δr1=700 m，ηDBmax=20。仿真結果如圖5～圖8所示。

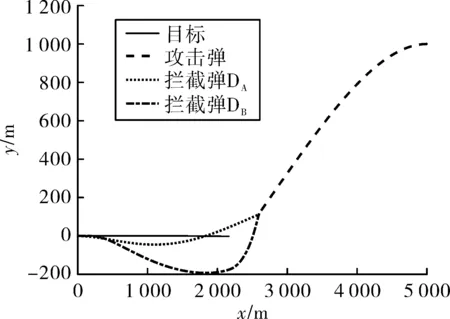
圖5 TCGL彈道圖

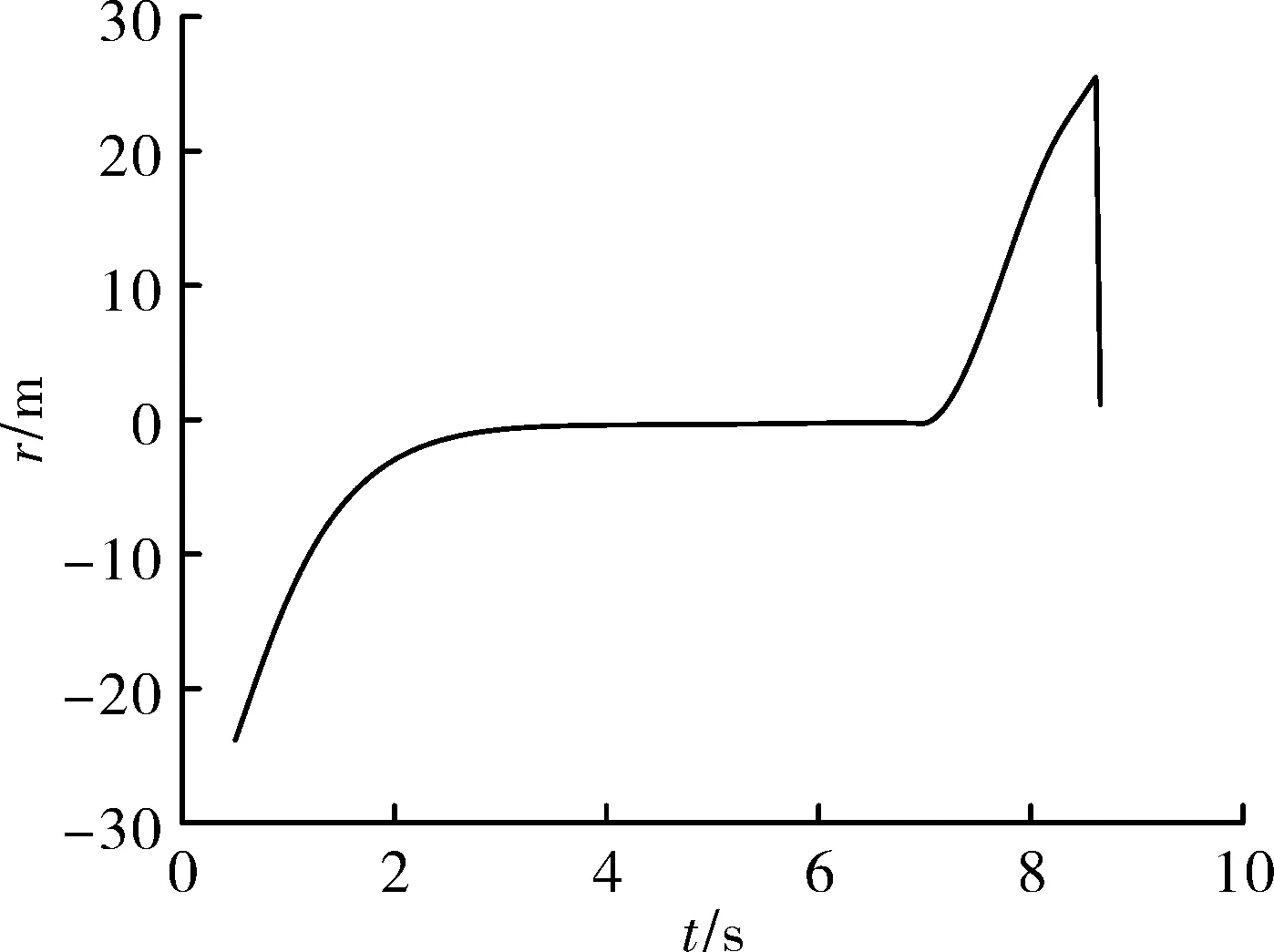
圖6 DA和DB的彈目距離差隨時間變化圖

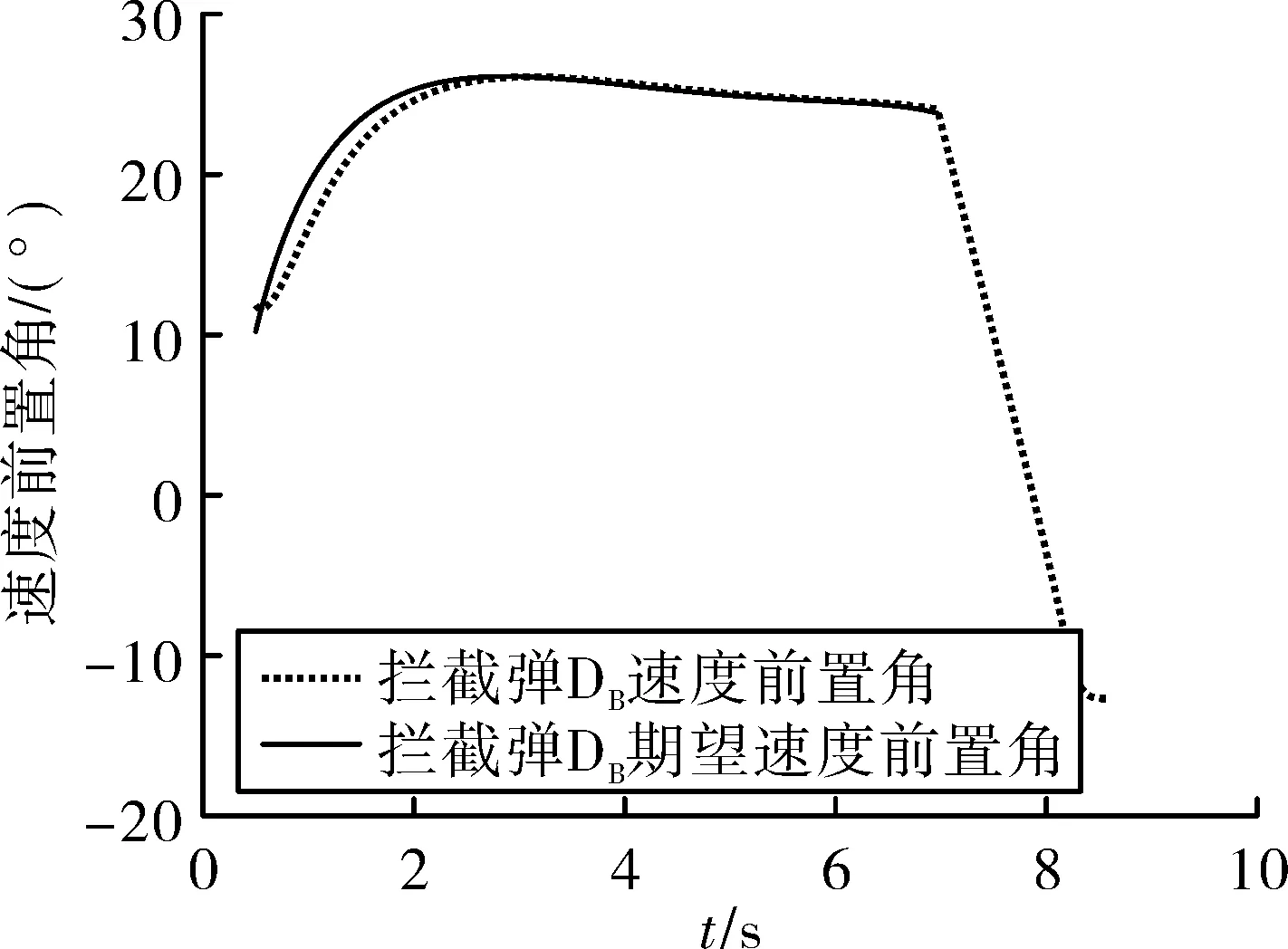
圖7 DB速度前置角變化圖

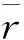
圖8 TCGL過載變化圖

4.3 Δt1優化結果及分析

結合上面分析，對Δt1進行優化。令d=0.01，e=1 000。設置經過20代迭代，每代10次尋優。邊界約束條件為：0.1 s≤Δt1≤5 s。其余仿真參數同上。

設計不同情形以研究Δt1的影響，場景2為d=0.01，e=0.01；場景3為d=0.001，e=1 000，場景2、3與前述場景1，即d=0.01，e=1 000，優化結果對比如表2所示。

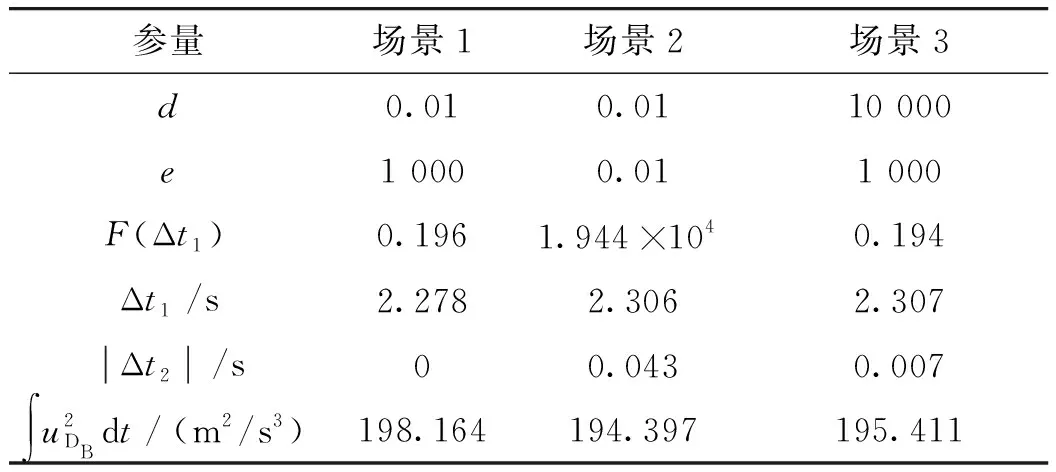
表2 3種場景下的優化結果

對比場景1和場景2，當e減小時，DB付出的能量相對于場景1減小2%。由場景1和場景3可知，當d減小時，|Δt2|=0 s，兩枚防御彈同時攔截M，參數d的改變對于整體結果影響較小，是由于Δt2較小，對于結果影響相對較小導致的。在該場景下，選取發射時間間隔為2.3 s左右即可實現最優。改變優化參數對于結果的選取影響不大，從側面證明了TCGL的適應性和參數的合理性。

5 結論

提出了一種新的協同防御策略。無人戰機順序發射兩枚防御彈，設計OCGL和TCGL攔截來襲彈，優化防御彈發射間隔，針對不同場景得到對應最優解。證明了OCGL攔截來襲彈的過載優勢，TCGL可實現兩枚防御彈同時攔截來襲彈，組合使用能增加對來襲彈的毀傷力度。