臨近空間無動力攻擊器彈道優化設計研究*

王瑩瑩，王 堅，岳韶華，何 蘋

(1 空軍工程大學防空反導學院，西安 710046； 2 西京學院信息工程學院，西安 710123)

0 引言

利用臨近空間平臺的高度和速度優勢，發射無動力攻擊武器，打擊空中高價值目標，是一種有前景的選擇[1-7]。對臨近空間無動力攻擊器(以下簡稱臨空攻擊器)彈道進行優化設計，是獲取攻擊器良好戰技性能的有效途徑。

和航空制導炸彈類似，臨空攻擊器也僅依靠載機的發射高度和速度來打擊目標。因此，可參考航空制導炸彈，對臨空攻擊器的彈道進行設計。工程上常用的航空制導炸彈彈道方案分為兩個階段：滑翔段和俯沖段。在滑翔段，制導炸彈按照最大升阻比對應的攻角滑翔飛行，在接近目標末端，采用比例導引的方式俯沖攻擊目標[8]。文獻[9-11]指出這只是一種經驗設計彈道，并不是理論上的最優彈道，設計初段按最佳升阻比滑翔、末段采用有約束比例導引飛行的彈道模式，認為該彈道模式可使制導炸彈獲得更遠的射程和更強的目標毀傷能力。

另外，臨空攻擊器與航空制導炸彈又存在較大差異。如美軍GBU-39小直徑炸彈，投放高度≤12 km，投放速度≤1.6Ma，GBU-39從投放到命中目標都處于航空空間[12]。而臨空攻擊器發射高度30～50 km，發射速度3～6Ma，從發射到命中目標跨越臨近空間和航空空間[6-7]。這些不同點使得臨空攻擊器與航空制導炸彈戰技性能差異較大，并且彈道呈現出不同的特點。

因此，文中借鑒航空制導炸彈彈道優化設計經驗，并結合臨空攻擊器具體特點，設計臨空攻擊器彈道方案，采用均勻試驗設計、偏最小二乘法、基于懲罰函數的遺傳算法等綜合方法，對臨空攻擊器彈道優化設計問題進行求解。

1 彈道方案設計

臨空攻擊器從發射點到命中目標點有多條彈道。彈道優化設計就是從這些彈道中選一條理想彈道，使攻擊器具有良好的氣動升阻特性、制導控制效率和攻擊路線，并使攻擊器射程、平均速度、末速度、法向過載、彈著角等戰技術性能參數滿足作戰需求。

臨空攻擊器飛行跨越臨近空間和航空空間。對于攻擊器發射高度在40～50 km范圍的情況，查美國1976大氣標準，表1為40～50 km高度大氣相對密度，其中h為高度，ρ為對應高度大氣密度，ρ0為海平面大氣密度，ε=ρ/ρ0。

表1 40～50 km高度大氣相對密度

由表1可知，40～50 km高度空域空氣極其稀薄，在42 km高空，大氣密度僅為海平面的2.4‰。臨空攻擊器在40～50 km高度空域飛行時，氣動力控制效率很低。通過大量仿真計算對比，40 km高度以下，攻擊器才具備氣動控制效率。因此，需研究攻擊器在40～50 km高度空域飛行時，采用何種飛行彈道更為合適，并確定下滑攻角α1、側滑角β1的值。

從40 km高度開始，攻擊器彈道方案規劃為滑翔段和有角度約束比例導引段。

在滑翔段，使攻擊器以攻角α2滑翔飛行，主要目的是最大限度增加射程，此段飛行結束高度為hm1。攻角α2不能過大，攻角大固然可以提高升力，但同時會產生過多的誘導阻力，對提高射程反而不利，而且攻角過大會導致攻擊器系統不穩定，但α2太小又不能起到明顯的增程效果。另外，單從射程上來講，當攻擊器發射初始條件給定時，hm1越小則射程越遠，但hm1過小會使末制導控制段時間太短，滿足不了末制導要求。因此，需明確α2和hm1的值。

在有角度約束比例導引段，為了增強攻擊器的突防能力和毀傷目標能力，希望攻擊器的末制導段越陡峭越好，即彈著角要盡可能大。

考慮到命中角約束，將期望命中角修正量引入比例導引規律，縱向帶有末端姿態角約束的制導律為[10，13]：

(1)

式中：k為縱向視線角速度比例系數;k1為期望命中角修正比例系數；θF為期望彈著角，取90°。由于偏航平面內不需要進行角度約束，所以該平面內導引律形式不需要修正項。式(1)等號右邊第二項，就是期望命中角修正量，顯然其大小和當前視線角q、期望彈著角θF都有關系，所以只要k、k1選取的適當，就會使末端彈著角達到要求。

需要說明的是，發射高度在30～40 km之間的攻擊器彈道優化方案規劃為滑翔段和有角度約束比例導引段，與以上分析過程類似，不再單獨分析。

2 彈道優化數學描述

通過以上彈道方案設計，可以使臨空攻擊器在射程、末速度、平均速度等戰技性能指標滿足作戰需求的前提下，有更大的彈著角。其中需優化的變量包括：攻擊器在40 km以上高度飛行時的飛行攻角α1、側滑角β1，攻擊器在40 km以下高度飛行滑翔段攻角α2、滑翔段飛行結束高度hm1，比例導引系數k以及期望命中角修正比例導引系數k1。攻擊器彈道優化數學描述如下：

(2)

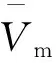
3 攻擊器動力學方程

在常規彈道模型的基礎上，綜合考慮高空空氣動力、重力加速度隨高度與緯度的變化、地球曲率及自轉等因素的影響，得到臨空攻擊器質心在發射坐標系下的動力學方程組為[6,14-15]：

(3)

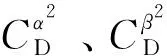
4 仿真算例及分析

參考文獻[4]和文獻[7]，表2為假定的發射參數。

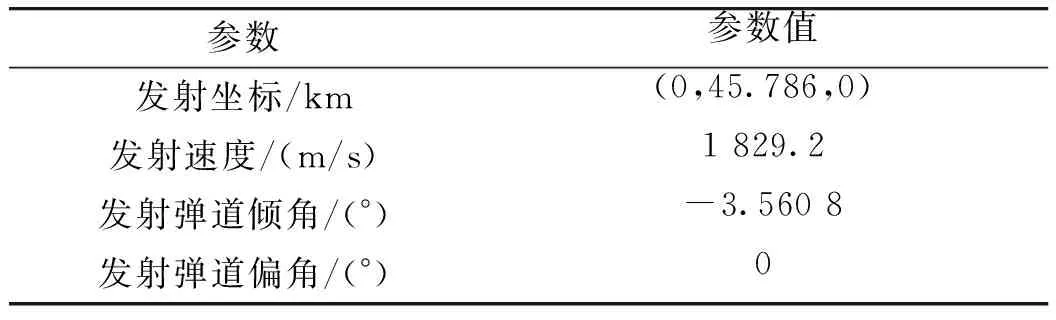
表2 發射參數

4.1 攻擊器在40 km以上高度飛行段彈道優化仿真

為了考察飛行攻角α1、側滑角β1的值對攻擊器彈道的影響，現假設如下仿真想定：攻擊器從發射點飛行至40 km高度飛行段采用固定攻角α1、側滑角β1飛行的方式，從40 km高度到命中目標采用標準比例導引彈道，目標在10 km高度以50 km為半徑作巡航飛行。表3為仿真計算參數。

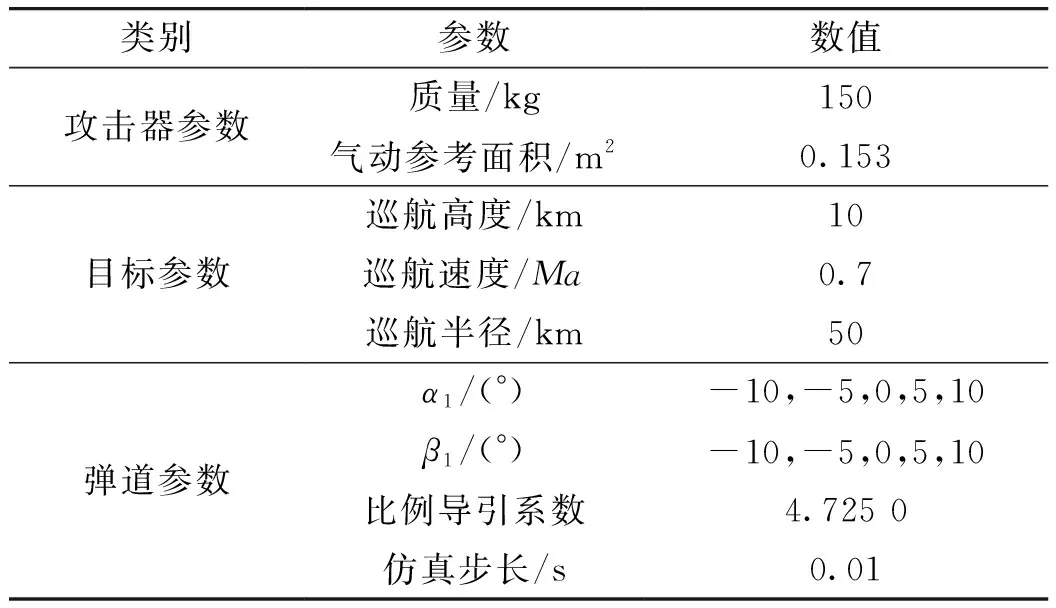
表3 仿真初始條件

當攻擊器參數、發射條件、目標參數相同，α1分別取-10°、-5°、0°、5°、10°，β1分別取-10°、-5°、0°、5°、10°時，三自由度理想彈道仿真對比如圖1所示。攻角隨高度變化的對比如圖2所示，側滑角隨高度變化的對比如圖3所示，水平平面法向需用過載與可用氣動過載的對比如圖4所示，垂直平面法向需用過載與可用氣動過載的對比如圖5所示。

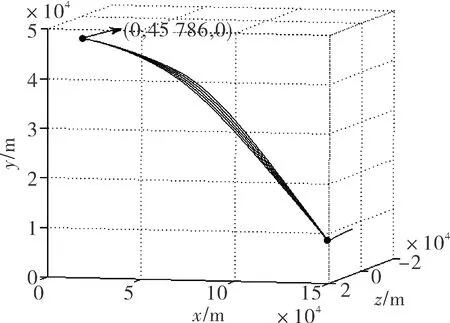
圖1 不同α1、 β1對應的彈道對比

圖2 不同α1、 β1對應的攻角變化對比

綜合分析圖1～圖5可知，α1、β1分別取不同值時，對應攻擊器全彈道、全彈道垂直平面法向過載、水平平面法向過載，以及在40 km以下高度，攻擊器攻角、側滑角均相差較小。因此可得以下結論：對于發射高度大于40 km的臨空攻擊器，在40～50 km高度空域飛行時，只要需用過載小于可用氣動過載，下滑攻角α1、 下滑側滑角β1可以在[-10°,10°]范圍內任意取值，最節約能量的方式是α1=0°、β1=0°，攻擊器采用慣性飛行的方式。

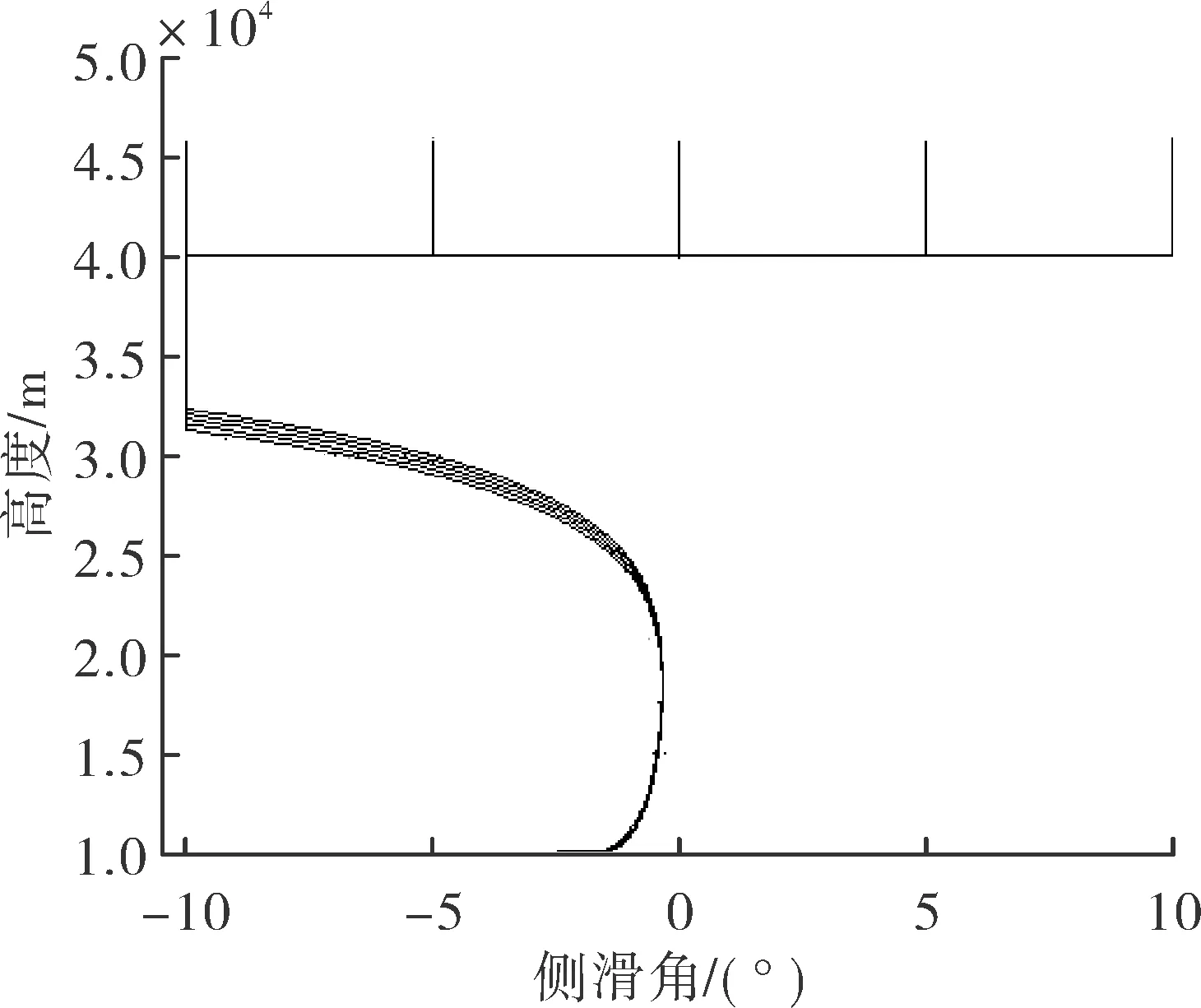
圖3 不同α1、 β1對應的側滑角變化對比

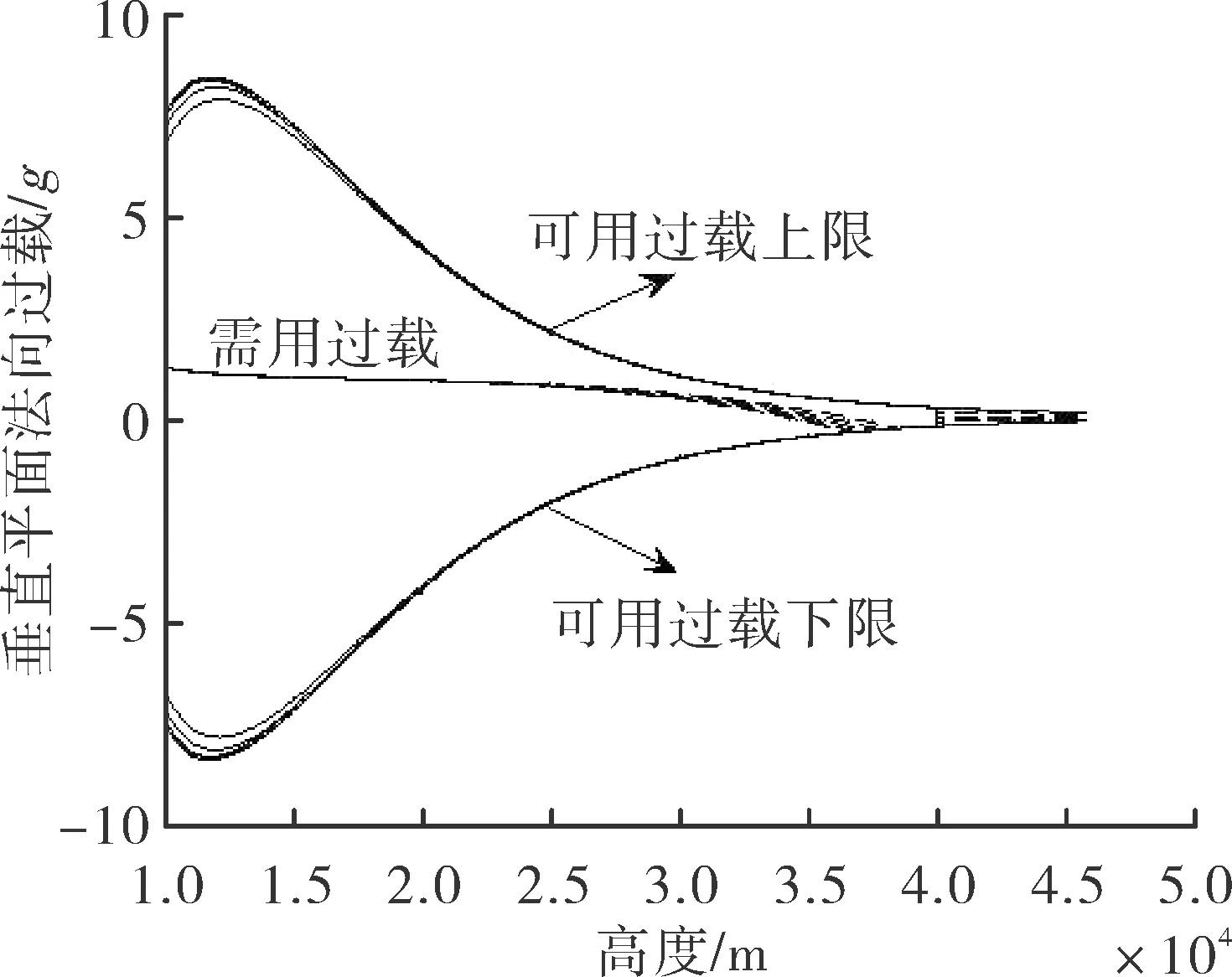
圖4 不同α1、 β1對應的垂直平面法向過載對比

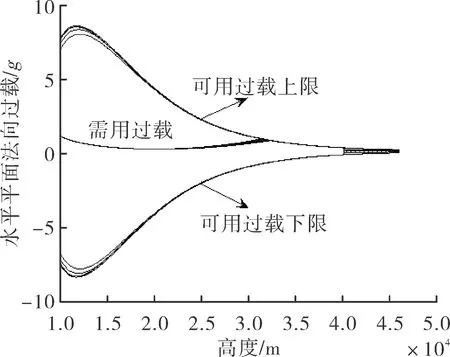
圖5 不同α1、 β1對應的水平平面法向過載對比

4.2 攻擊器在40 km以下高度飛行段彈道優化仿真

從40 km高度開始，攻擊器以較大攻角α2滑翔飛行，此段飛行結束高度為hm1。從hm1高度開始，進入末制導階段，末制導階段縱向制導引入具有姿態角約束的比例導引律，對攻擊器在40 km以下高度飛行段彈道優化設計進行仿真計算，計算流程如圖6所示[3，7]。

通過優化計算，得到優化解：α2=7.763 4°，hm1=29.444 km，k=3.001 2，k1=0.022 0。

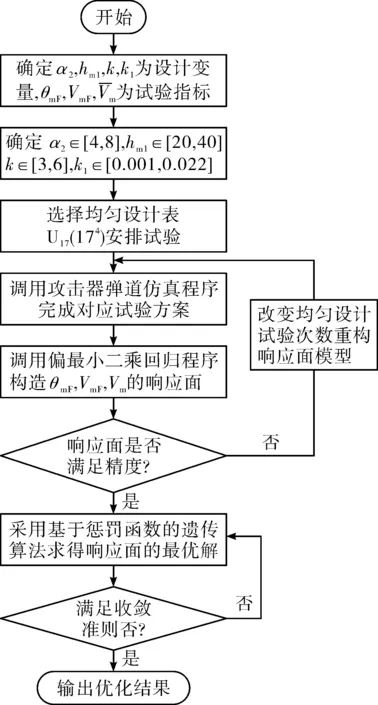
圖6 彈道優化仿真計算流程圖

綜上分析，得到發射高度hf為45.786 km、發射速度VmF為1 829.2 m/s、發射彈道傾角θf為-3.560 8°、發射彈道偏角ψv為0°的臨空攻擊器彈道優化結果如圖7所示。

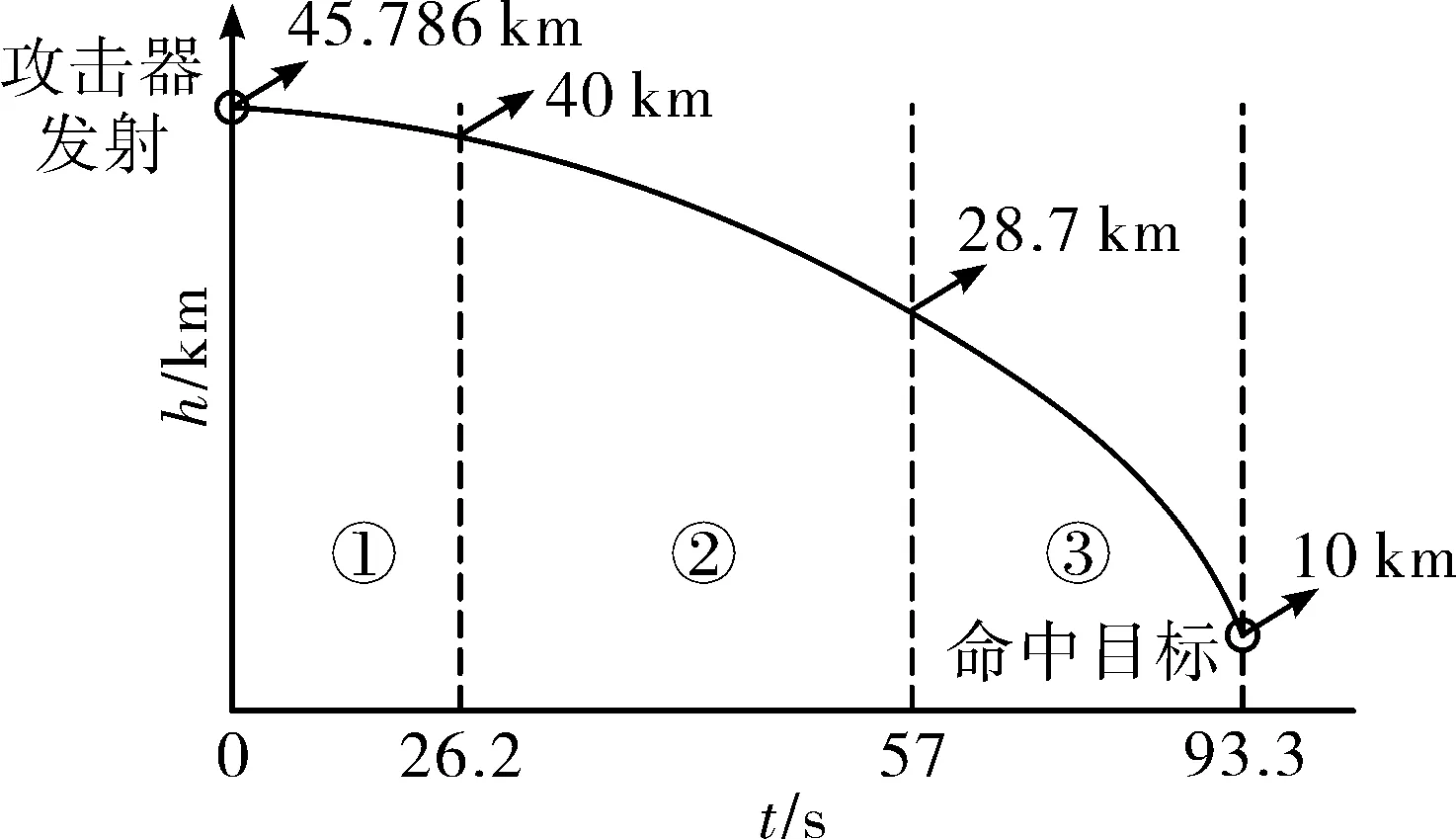
圖7 彈道優化設計結果示意圖

圖7中，攻擊器從發射點到命中目標的優化彈道為：1)0～26.2 s時間段，攻擊器飛行高度由發射高度45.786 km下降至40 km，采用慣性飛行方式，攻角0°，側滑角0°。2)26.2～57 s時間段，攻擊器飛行高度由40 km下降至28.7 km，垂直平面內，攻擊器以7.763 4°攻角滑翔飛行；水平面內，按標準比例導引律飛行。3)57～93.3 s時間段，攻擊器飛行高度由28.7 km高度降至目標巡航飛行高度10 km，垂直平面內，按有角度約束比例導引律飛行；水平面內，按標準比例導引律飛行。

臨空攻擊器彈道優化前后對比如圖8所示。

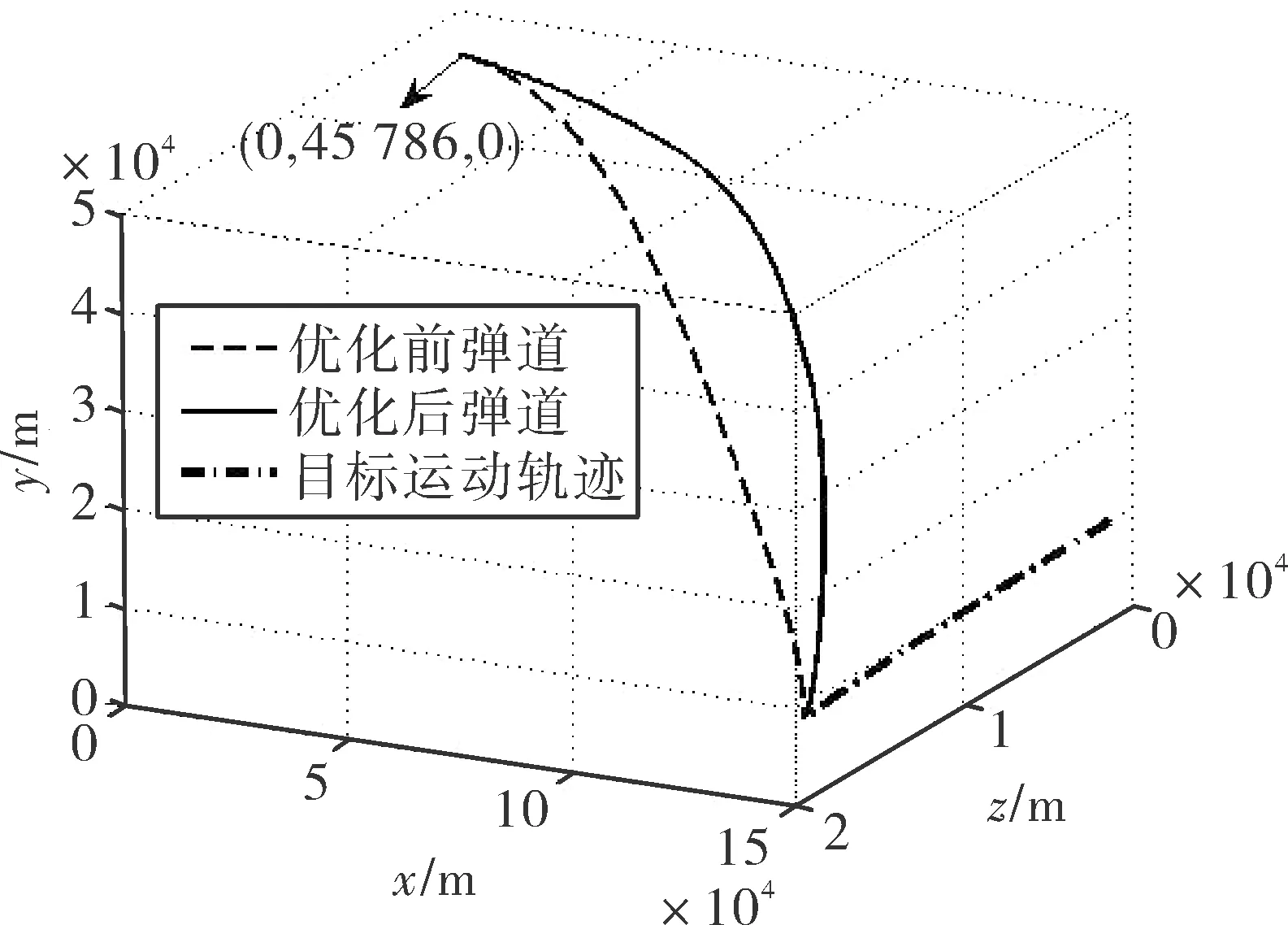
圖8 彈道對比圖

優化后的彈道與優化前相比，前段彈道更為平緩，達到了滑翔增程的目的，后段飛行彈道更為陡峭，增強了攻擊器的突防能力和目標毀傷能力。表4為彈道優化前后，臨空攻擊器飛行性能對比。

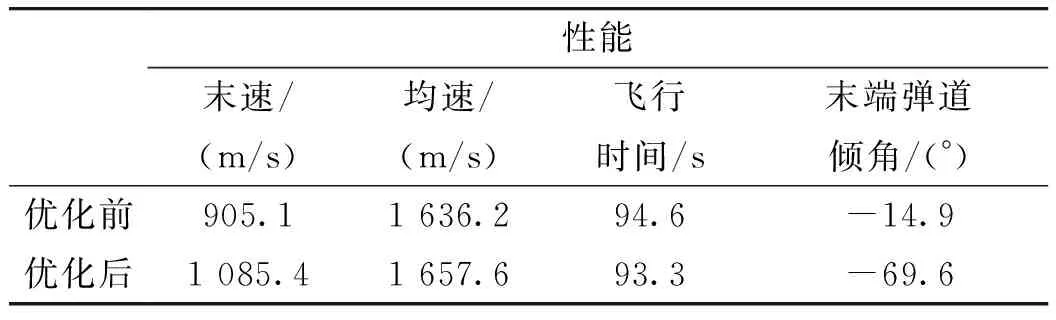
表4 彈道優化前后攻擊器飛行性能比較

由表4可看出，彈道優化后攻擊器末速度、平均速度有所提高，飛行時間有所縮短，且都滿足作戰需求，同時攻擊器末端彈道傾角絕對值大幅增加，達到了彈道優化的目的。

5 結論

對臨空攻擊器彈道進行了優化設計，優化后的彈道分為三段：慣性飛行段、滑翔增程段、有角度約束比例導引段。攻擊器發射高度在40～50 km范圍時，攻擊器飛行高度在40 km以上飛行段，采用慣性飛行彈道，攻擊器最省能量、平穩飛行的方式是飛行攻角為0°、側滑角為0°；攻擊器飛行高度在40 km以下飛行段，采用滑翔和有約束比例導引飛行彈道，可以達到既增加射程，又保證更大的彈著角命中目標的目的。研究結果對于臨近空間裝備發展具有一定牽引作用。