蟻群算法在室內地磁定位中的應用

郭燕莎

（天津職業技術師范大學信息技術工程學院，天津 300222）

室內定位作為移動互聯網發展的應用領域之一，正在直接或間接地影響著人們的工作和生活。在生活中可用來監控老人和小孩的活動，可為殘疾人提供實時的導航幫助，并在危急時刻自動求助；在購物時可協助用戶便捷獲取需求商品的位置和信息；在困境中可及時引導救援人員快速解救危難者；在參觀時可為游客實時展現作品信息。此外，室內定位還可應用于醫療管理、公共事務和網絡安全等領域。室內定位的廣闊前景吸引著國內外眾多學者和機構對其進行研究和探索。超聲波[1]、紅外線[2]、射頻識別[3]、WIFI[4]、Zigbee[5]和藍牙[6]等是常用的室內定位技術，定位精度較高，且各有優缺點和適用場合，但共同特點是需預先在環境中安裝無線網絡或額外設備，以接收和發射信號，再按照多邊測量或指紋匹配等算法實現定位。前期準備和后續維護工作將耗費一定的時間以及人力、物力和財力。

利用和挖掘環境中現有資源進行室內定位已然成為學者關注的焦點和努力的方向。不同研究者根據具體需求和環境特征提出了單一和融合的室內地磁定位，精度較高，可滿足一定的位置服務需求。Haverinen 等[7]基于地下鐵礦石引起的地磁異常，采用蒙特卡羅算法實現地下采礦環境定位，該技術可為基礎設施要求較低的地下環境提供一種高效的定位方案；申文波[8]通過改進粒子濾波算法融合地磁指紋和慣性傳感器信息進行室內定位研究，實現了2 m的定位精度；周家鵬等[9]通過克里金插值算法，在環境中建立地磁數字基準圖（地磁值模），然后利用動態時間規整算法實現室內定位，具有較高的理論和實際應用價值；李思民等[10]在手機室內定位系統中融合了PDR 和地磁指紋信息，實現了2 m 的定位精度；而宋宇等[11]為了進一步提高精度，在WIFI 和PDR 組合定位的基礎上又融合了地磁指紋信息，使平均定位誤差降低至1.41 m；張文杰[12]采用改進的粒子濾波算法融合RFID 和地磁指紋信息進行室內定位，1 m 內的累積概率達82%。上述定位過程均使用了地磁指紋匹配，但并未考慮隨時間和外圍環境而變化的地磁特征、不同位置間某個或多個維度地磁屬性的相似性、不同位置間地磁值模的相似性等。基于地磁場的室內定位研究和應用還有待于進一步探索。針對目前地磁定位存在的問題，本文首次將蟻群算法引入室內定位的地磁指紋匹配過程，并通過實驗測試，比較了提出的6 種思路與最近鄰算法（k-nearest neighbor，KNN），結果表明蟻群算法應用于室內定位是合理和可行的，且位置識別率較高。

1 蟻群算法概述

蟻群算法是受自然界真實蟻群覓食過程啟發而提出的一種群智能算法。基本思路[13]為每只螞蟻在尋找食物的過程中，可感知路徑上已存信息素的同時，也會在路徑上留下信息素；而且每個個體都是朝著信息素強度高的方向移動，隨著時間推移，路徑越短信息素越強（因揮發少留存多），進而吸引其他螞蟻訪問的次數相應增多；久而久之，整個蟻群都可找到最短路徑的食物源，此為蟻群算法的目的所在，也即問題的最優解。室內定位原則是在環境中實時采集地磁屬性（測試數據），并分別與數據庫中每個位置的屬性值（訓練數據）進行比較，屬性越相似，其所在位置被匹配的概率就越大；測試數據與訓練數據間的相似度相當于蟻群算法中的信息素，所找到的信息素最強的位置即為與測試數據最接近的位置。二者的相似性是在室內定位中引用蟻群算法的直接原因。

蟻群算法已廣泛應用在監測網優化、旅行商問題[14]、物流配送[15]和車輛路徑規劃[16]等領域，并取得了顯著成果，但在室內定位中卻鮮有文獻描述。本文提出的6種思路，旨在通過蟻群算法提高定位過程中的地磁指紋匹配精度。

2 蟻群算法在室內定位中的應用

2.1 數據采集

本研究基于某工作區域8 個工位的地磁場（X，Y，Z）數據進行分析，采集數據位置如圖1 所示。該環境為典型的工作場所，配備有電腦、桌子、椅子、柜子和公用打印機等設施，工作時間啟用的公共設備和人員流動可能影響環境中的地磁屬性；總覆蓋面積約6 m2，不同工位間的最大距離為2.4 m，最小距離是1 m。

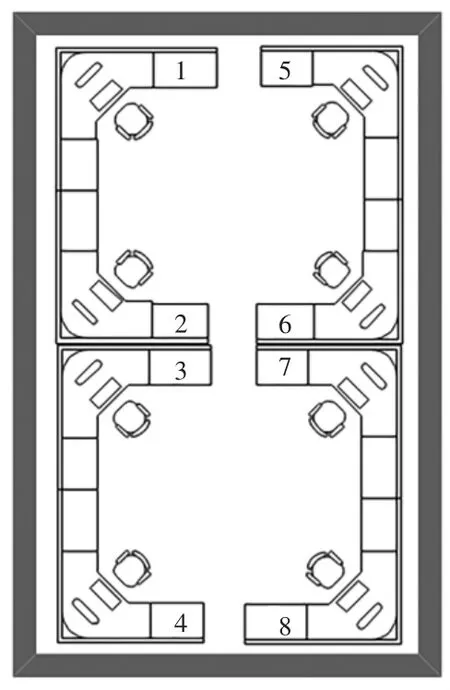
圖1 采集數據位置

數據采集過程：利用自主研發的手機APP 整點采集數據，工作日從9 點—21 點，周末從11 點—16 點，每個工位每次收集325 條記錄，共32 d。

數據處理過程：第1～16d 樣本是訓練數據，第17～32d 樣本為測試數據；由于直接采集的樣本波動較大，故首先對其進行卡爾曼濾波處理[17]，取較為穩定的最后25 條記錄作為當前時間點的訓練數據；而測試數據則取濾波后的最后1 條記錄，實驗中僅選用有代表性的 10 點（80 條記錄）、15 點（136 條記錄）和 21 點（80條記錄）的數據進行測試、比較和分析；其中，10 點和15 點為工作時間，環境較為嘈雜，21 點為非工作時間，環境較為簡單；每個工位的測試數據包括37 條記錄。

2.2 算法描述

本研究首次將蟻群算法引入室內定位的地磁指紋匹配過程，并通過實驗對提出的6 種定位思路和KNN 算法進行了比較。

2.2.1 基于KNN算法的定位思路

比較測試數據與不同位置訓練數據間的差異性，平均差值最小的位置即為測試數據所在位置。采用式（1）計算的歐式距離d 表示差異性程度，其值越小說明測試數據和訓練數據越相似；反之，差異性則越大。

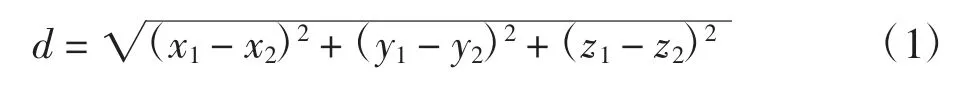
式中：（x1，y1，z1）和（x2，y2，z2）分別為測試數據和訓練數據的三維地磁屬性值。

由KNN 算法可知，與測試數據最相似或最接近的訓練數據所在位置即為當前測試數據的所屬位置，本算法適用于不同位置間的地磁屬性完全相異，同一位置不同時間點的地磁屬性基本一致。但由于地磁場易受環境因素影響，從而使得同一位置不同時段的屬性值可能相異，不同位置同一時段的屬性值可能相似，故室內定位中已不能完全依賴KNN 算法進行地磁指紋匹配。

2.2.2 基于蟻群算法的定位思路

根據特定規則選擇一個待選工位，將其地磁屬性與測試數據比較后，更新該位置信息素。每次迭代后，依據蒸發系數更新所有工位信息素，其中，信息素最大的工位即為當次迭代的測試數據所屬位置。完成指定迭代次數后，出現頻率最高的工位即為測試數據的最佳位置。具體執行步驟如下。

（1）參數設置和初始化啟發式因子

蟻群算法在地磁指紋匹配過程中的相關參數設置如表1 所示。

表1 蟻群算法在地磁指紋匹配過程中的相關參數設置

表1中：α 和 β 分別為信息素強度 τ 和啟發式因子 δ 在蟻群尋優過程中的相對重要性；ρ（0 ＜ ρ ＜ 1）為尋優路徑上留存信息素的蒸發系數；（1-ρ）為留存信息素的持久性系數[18]。

本文在初始化啟發式因子時考慮了2 種情況：①測試數據與每個工位訓練數據第1 條記錄的歐式距離倒數作為啟發式因子；②測試數據與每個工位相同時間點訓練數據第1 條記錄的歐式距離倒數作為啟發式因子。啟發式因子和距離值d 互為倒數，即測試數據與訓練數據的差異越小，啟發式因子越大。

（2）隨機選擇第1 個訪問目標和確定未訪問位置

每只螞蟻隨機選擇一個位置作為出發點，也就是m 只螞蟻隨機選m 個位置作為第1 個訪問目標。隨后每次迭代，每只螞蟻需遍歷所有工位與測試數據比較，故應先確定所有未訪問工位，然后再按照規則選出下一個待訪問目標。

（3）選擇下一個待訪問目標

選擇下一個待訪問目標并計算測試數據與待訪問位置訓練數據間的歐式距離和sum。分2 種情況選擇下一個待訪問目標，并針對如何從待訪問工位選擇訓練數據與測試數據相比較，提出了6 種思路。

情況1 從未訪問工位中隨機選擇下一個待訪問目標k。隨后，計算測試數據與待訪問工位訓練數據間的歐式距離和，選擇訓練數據的方式為：①Loc 算法，從待選工位的訓練數據中隨機選5 條記錄；②Loc_Time 算法，從待選工位的訓練數據中隨機選5 條與測試數據時間點一致的記錄。

情況2 依據信息素強度和啟發式因子，計算每個未訪問工位的狀態轉移概率Pk[18]，見式（2），并通過比較累積概率與生成的隨機數確定下一個待訪問目標k。

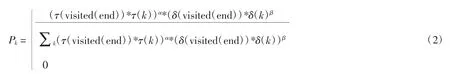
式中：visited（end）為最后 1 個已訪問位置；τ（visited（end））和 τ（k）分別為最后 1 個已訪問位置和第 k 個未訪問位置的信息素強度；δ（visited（end））和 δ（k）分別為最后1 個已訪問位置和第k 個未訪問位置的啟發式因子。

隨后，計算測試數據與待訪問工位訓練數據間的歐式距離和，選擇訓練數據的方式為：①Loc_Prob算法，從待選工位訓練數據中隨機選5 條記錄；② Loc_Time_Prob 算法，從待選工位訓練數據中隨機選5 條與測試數據時間點一致的記錄；③Loc_Prob_Diff 算法，根據待選工位在有序信息素中的順序，依據代碼的設置規則確定從訓練數據中選的記錄數；④Loc_Time_Prob_Diff 算法，根據待選工位在有序信息素中的順序，按照同樣規則確定從訓練數據中選幾條與測試數據時間點一致的記錄。

從訓練數據中選擇記錄數的設置規則：

%order 是當前工位在有序信息素中的順序號

%Loc_Prob_Diff 算法：num 是選定待訪問工位訓練數據的總記錄數

%Loc_Time_Prob_Diff 算法：num 是選定待訪問工位訓練數據中與

%測試數據時間點一致的總記錄數

if order＞=1&order ＜3

visitP=randperm（num，8）；

elseif order ＞=3&order ＜6

visitP=randperm（num，6）；

else visitP=randperm（num，4）；

（4）更新不同位置的信息素

更新當前位置的信息素，信息素是蟻群覓食過程中彼此溝通的媒介。根據訓練數據與測試數據間的相似度（歐式距離），更新當前位置的信息素[3]。

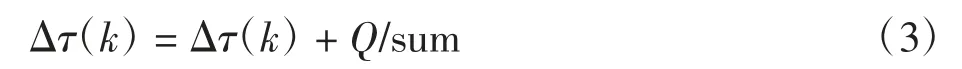
式中：Δτ（k）為第k 個工位的信息素更新量。

每次迭代時，測試數據均與所有工位比較；隨后，依據相似度更新每個位置的信息素。螞蟻覓食規則：在追蹤信息素尋找食物的過程中，信息素也在不斷揮發；將此遷移到位置尋優中，按式（4）完成所有工位的信息素更新。

將信息素強度按從大到小的順序排序，信息素強度越大，說明測試數據越接近該位置的地磁屬性；Loc_Prob_Diff 算法和Loc_Time_Prob_Diff 算法正是根據這個排序結果，確定從訓練數據中選擇記錄與測試數據進行比較的。

（5）獲得測試數據的最佳位置

獲取本次迭代中信息素最大的位置：由式（3）和式（4）可知，測試數據與訓練數據間的差距越小（越相似），信息素強度則越大，故信息素強度最大的工位極有可能是測試數據的所屬位置。

統計所有迭代中出現次數最多的位置：每次迭代完，都可獲取到當次迭代的最佳位置；多次迭代后，出現次數最多的即為測試數據所屬的最佳位置。

2.3 結果比較與分析

本研究在某工作區域采集了不連續的32d 地磁數據進行實驗測試，跨度較大，覆蓋較全。以下將分別從不同時間點的定位精度、不同工位的正確匹配數和不同算法迭代過程中識別的正確工位數3 個方面進行分析和討論。

2.3.1 不同時間點的定位精度

不同算法的定位精度比較如表2 所示，其中，第2列為本文提出的6 種思路和KNN 算法的室內定位精度，第3-5 列分別表示在10 點、15 點和21 點的位置識別率。從表2 可知，KNN 算法的定位精度最低；Loc、Loc_Time、Loc_Prob、Loc_Time_Prob 和 Loc_Prob_Diff算法的定位精度類似，彼此間的差距為0.68%～2.37%；Loc_Time_Prob_Diff 算法的地磁指紋匹配過程融合了上述5 種思路的定位細節，其總體定位精度最高，可達82.77%。

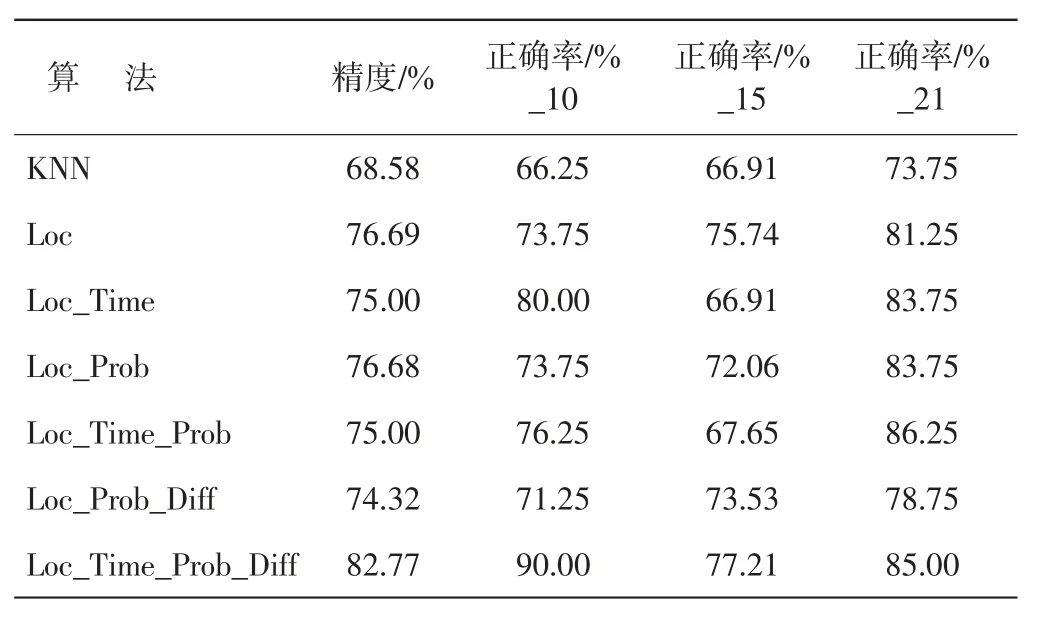
表2 不同算法的定位精度比較

由于每個時間點測試數據包含的記錄數不同，故位置識別率的計算方式為某時間點的正確位置匹配數與該時間點測試記錄總數的比值。本文提出的6 種思路在不同時間點的位置識別率均高于KNN 算法。除Loc_Time_Prob 算法在21 點的位置識別率略高于Loc_Time_Prob_Diff 算法外，后者在定位精度和3 個時間點的位置識別率均高于其他算法。總體上，21 點的位置識別率最高，Loc_Time、Loc_Prob、Loc_Time_Prob和Loc_Time_Prob_Diff 算法在10 點的位置識別率高于 15 點，而 KNN、Loc 和 Loc_Prob_Diff 算法則正好相反，但差別不大。其原因是10 點和15 點屬于正常工作時間，環境中啟動的機器設備和密集的人員流動導致地磁場波動較大，從而使得同一位置不同時段的地磁屬性不一致或不同位置間的地磁屬性相互干擾，造成位置匹配率降低；而21 點則是非工作時間，工作場所中僅有少量的人員活動和設備啟動，降低了環境對地磁場的影響程度，位置識別率也就相應提升。總之，室內的地磁屬性隨時間和環境狀態而變，導致室內地磁定位精度也隨之改變。

2.3.2 不同工位的正確匹配數

測試數據中每個工位都有37 條記錄，本研究分別統計了不同定位算法識別每個工位的正確率。基于不同算法獲取的正確位置匹配數如表3 所示，從表3可知，工位 1（8.1%～56.8%）和工位 7（2.7%～73%）的正確匹配數最低，工位8 的正確匹配數（66.7%～73%）次之；工位2 的每條測試數據均可得到正確匹配位置（100%）；工位 3、4 和 5 的正確位置匹配數較高（89.2%～100%），而工位 6 則略低（83.8%～94.6%）。

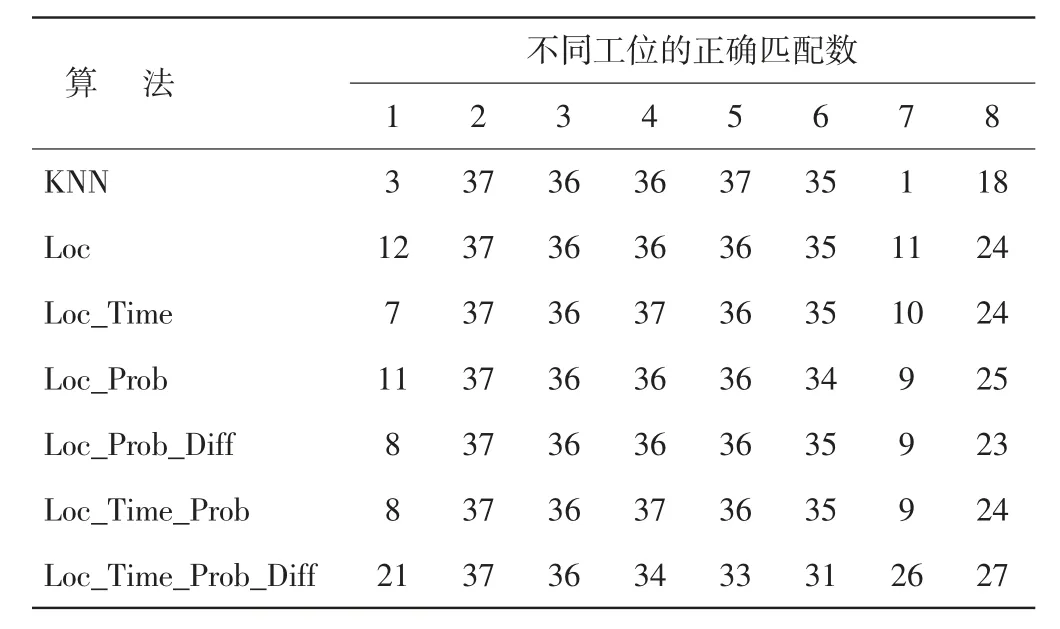
表3 基于不同算法獲取的正確位置匹配數

KNN 算法作為典型的位置指紋匹配方法，只要不同位置間的屬性值完全相異，同一位置不同時間點的屬性值基本相同，KNN 算法便可精確地進行位置識別。從表3 中可以看出，因工位2-6 的地磁屬性較為獨立，干擾較少，故KNN 算法對其識別率較高；而工位1、7 和8 的地磁屬性波動較大，且受環境干擾多，相應地，KNN 算法的識別率就較低，尤其是工位1 和工位7。本文提出的6 種算法不僅可以保持對易識別工位的高匹配率，同時又可提高對工位1、7 和8 的識別率。值得注意的是：Loc_Time_Prob_Diff 算法雖對工位4-6 的識別率略低于KNN 算法，但卻大幅提高了對工位1、7 和8 的位置匹配度，其識別率分別增長了48.6%、67.6%和24.3%。

2.3.3 不同算法迭代過程中識別的正確工位數

不同算法迭代過程中的位置識別數如圖2 所示。較為明顯的是Loc_Time_Prob_Diff 和Loc_Prob_Diff 算法，前者從第2 次迭代開始每次識別出的正確位置數都遠超過其他算法，且自第3 次迭代后，每次的位置識別數較為穩定（最大值：245，最小值：225）；后者在大部分迭代過程中的位置識別數均低于其他算法，且波動較大（最大值：220，最小值：194）。其他4 種算法每次迭代時的位置識別數較為相似，且變化幅度不大（最大值：227，最小值：214）。

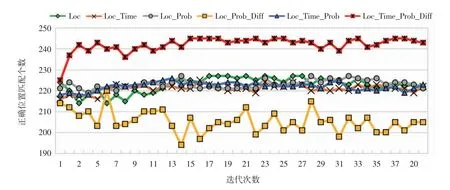
圖2 不同算法迭代過程中的位置識別數

3 結 論

本文提出了基于蟻群算法的6 種室內地磁指紋匹配思路，并在某工作環境中對其和KNN 算法進行了測試、比較和分析，得出的結論如下。

（1）當不同位置間的屬性值差異較大，且同一位置不同時間點的屬性值基本一致時，KNN 算法的定位精度較高。

（2）當不同位置間的屬性值較為相似，或同一位置不同時間點的屬性值受環境干擾較大時，KNN 算法失效；而本文提出的地磁指紋匹配思路既可保持對易識別位置的高匹配率，又可提高對受干擾位置的識別率。

（3）Loc_Time_Prob_Diff 算法在執行過程中，同時考慮了每個位置在不同日期但同一時間點地磁屬性的相似性、不同位置具有不同的訪問概率、與測試數據相似度不同的位置被訪問次數也不同，從而增加了受干擾位置的被訪問頻率，以達到提高定位精度的目的。

（4）不同時間點和不同位置的地磁屬性受環境干擾程度不同，定位精度也不同。一般情況下，工作時間的定位精度低于非工作時間，清凈和干凈位置（受人員流動和外圍設備的影響較小）的定位精度較高。

地磁指紋匹配算法是室內地磁定位的關鍵，本文提出的思路可與其他定位過程相結合進行更深入的研究和探索，以期更好地提高定位精度和拓展應用領域。