跨坐式單軌車輛的臨界橫向力與曲線限速

張 讓，任利惠，季元進

(同濟大學 鐵道與城市軌道交通研究院，上海 201804)

跨坐式單軌列車的主要優點之一是曲線通過能力強，最小通過曲線半徑在50 m左右。跨坐式單軌車輛的導向輪和穩定輪水平鉗住軌道梁側面，起著導向和穩定車輛的作用[1]，車輛在通過曲線路段時，由于超高、離心力和軌道不平度的存在，導向輪、穩定輪的徑向力會發生較大變化，走行部的穩定輪或導向輪可能會離開軌面；車輛的曲線通過性方面,導向輪的受力情況是評價其運行穩定性的主要指標[2]。文獻[3]表明導向輪和穩定輪需要設置一定的初始預壓力以確保跨坐式單軌車輛能夠穩定運行，文獻[4]通過建立車橋系統的空間耦合振動模型，說明了穩定輪預壓力對車輛系統的響應影響很大。針對如何對導向輪和穩定輪的預壓力進行合理取值，文獻[5-6]通過建立跨坐式單軌車輛的多體動力學模型進行仿真計算，但是沒有給出用于指導車輛設計的明確數學公式。

一方面，要對跨坐式單軌車輛的導向輪和穩定輪設置合理的預壓力，確保車輛安全穩定地通過曲線路段；另一方面，也應對單軌車輛通過曲線時的速度進行限制。目前,關于跨坐式單軌車輛的曲線限速通過參照輪軌系統的曲線限速公式進行限制[7]。車輛曲線通過的速度限制，不僅取決于脫軌安全性和傾覆穩定性等指標，同時也受限于運行的舒適度。車輛通過曲線時產生的離心加速度也直接影響乘坐舒適度。未平衡的離心加速度往往使旅客感到不適，甚至造成旅客暈車[8]。因此，單軌車輛的曲線限速要考慮車輛的未平衡離心加速度和舒適度之間的聯系。

本文從車輛的乘坐舒適度角度討論單軌車輛的曲線限速問題。采用達朗貝爾原理將單軌車輛通過曲線的動力學問題轉換為靜力學問題，根據穩定輪剛剛脫離軌面這一臨界狀態，推導臨界橫向力和穩定輪預壓力之間的關系公式，得出未平衡的離心加速度與穩定輪預壓力之間的關系。在此基礎上，從車輛乘坐舒適度的角度討論穩定輪預壓力的合理取值問題，分析穩定輪預壓力、軌道梁超高率以及曲線半徑與最大曲線限制速度和最小曲線限制速度之間的關系。

1 臨界橫向力

1.1 車輛受力分析

當車輛行駛在圓周曲線路段時，向心力給車輛提供一個指向圓心的加速度，根據達朗貝爾原理，把車輛通過曲線的動態問題轉換為靜力學平衡的問題進行分析求解。

車輛以恒定速度通過圓曲線路段時的受力分析，見圖1，以穿過軌道梁表面中心并垂直于軌道梁表面為z軸，以軌道梁上表面水平線為y軸，建立直角坐標系；車輛模型主要包括車體橫移yc、車體側滾φc、轉向架橫移yb和轉向架側滾φb共四個自由度，由于轉向架質量遠小于車體質量，故將慣性力全部施加在車體質心上。

當車體在慣性力Fc作用下發生傾斜后，車體和轉向架重力的垂向分力變化量很小，因此可以忽略車體和走行部構架浮沉位移量的變化。將二系懸掛裝置等效為成線性彈簧，通過計算將其兩邊的橫向剛度合成一個總剛度Ksy[9]，因只針對車輛運行穩定性和舒適性，為減少建模的自由度，可以將跨坐式單軌車輛的輪胎線性化[10]。以圖1所示的車輛受力模型為研究對象，此時導向輪和穩定輪與軌道梁處于接觸狀態，根據達朗貝爾原理，可列以下平衡方程：

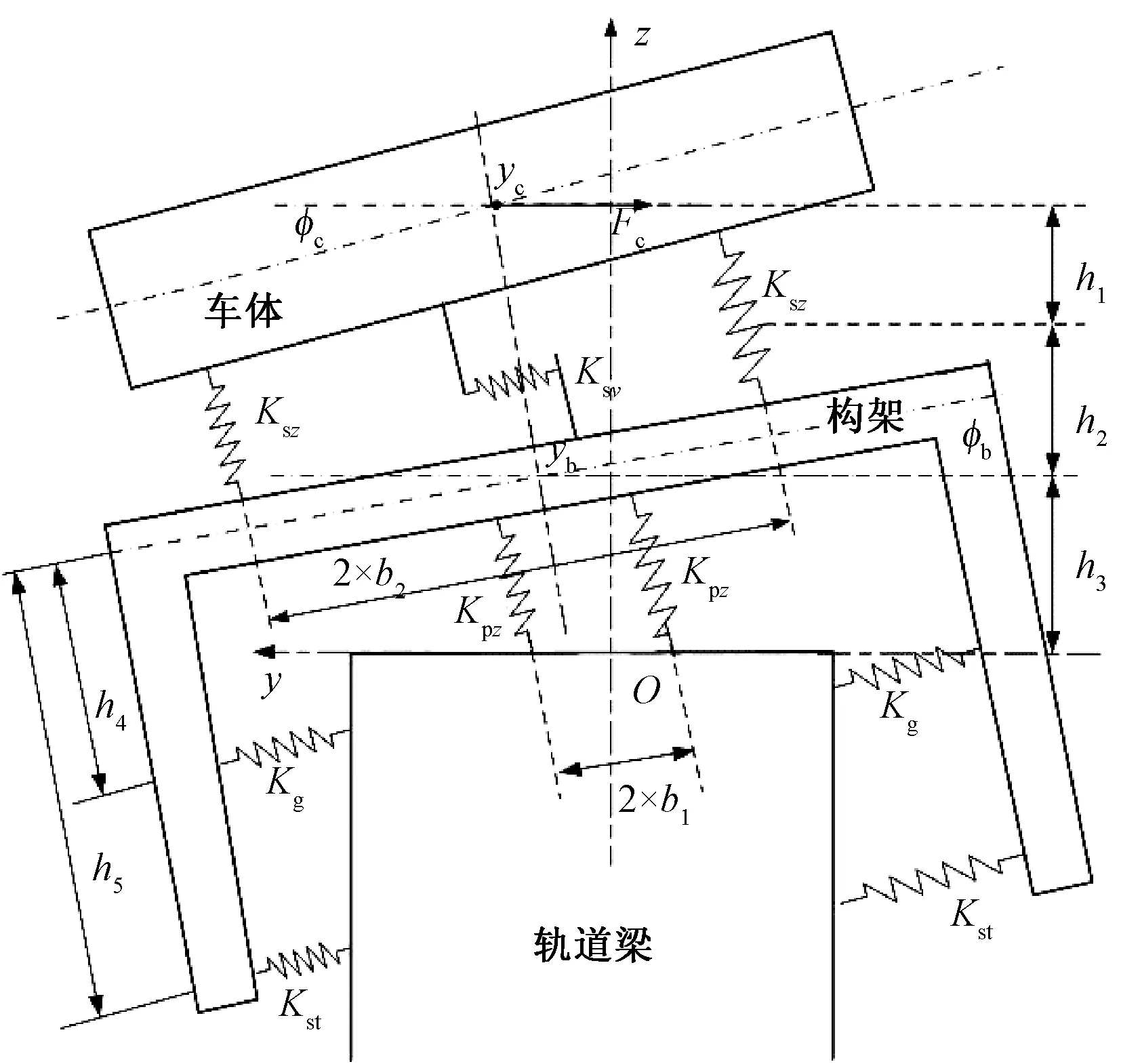
圖1 車輛受力分析示意圖

車體橫移方程

4Ksy(yc-yb)-Fc(1-φb)-G1φb=0

(1)

式中：Ksy為車輛二系懸掛橫向剛度；yc為車體橫移量；yb為轉向架橫移量；Fc為慣性力；G1為車體重量；φb為轉向架側滾角。

車體側滾方程

(2)

式中：Ksz為車輛二系懸掛垂向剛度；b2為二系彈簧中心線橫向跨距之半；φc為車體側滾角；h1為車體重心距二系彈簧的高度；h2為二系彈簧上支撐面距軌面的高度。

構架橫移方程

(3)

構架側滾方程

0.5G1(yc-yb)+2Kszb22(φc-φb)+2Ksy(yc-yb)h2+

2Kg[yb-(h3+h4)φb]h4+2Kst[yb-(h3+h5)φb]h5-

2Kpzb22φb-[0.5(G1+2G2)φb]rd+G2yb-

(4)

式中：Kpz為車輛輪胎垂向剛度；rd為走行輪輪胎半徑。

將式(1)～式(4)寫成矩陣形式

(5)

式中：

求解矩陣式(5)，得到車輛在慣性力Fc作用下的橫移量和側滾角度為

(6)

導向輪和穩定輪離開軌道梁側表面的位移分別為

(7)

由于h5>h4，所以穩定輪先脫離接觸軌道梁側表面。

表1 車輛模型主要參數及數值

1.2 臨界橫向力

當車輛行駛在圓周曲線路段時，如果速度大于或小于均衡速度，則車體在離心力的作用下向曲線外側或內側傾斜，速度繼續增大或者減小，車體傾斜的角度逐漸增大。當作用在車體上的離心力增至使走行部的一個穩定輪剛剛離開軌面時，其上的載荷恰好為零，定義此時作用在車體上的慣性力為臨界橫向力。臨界橫向力反映了跨坐式單軌車輛運動狀態的變化。當車體上的慣性力小于臨界橫向力時，走行輪兩側的穩定輪都與軌道梁接觸，車輛的抗傾覆能力保持在最大狀態，運行安全性得到保證；當車體梁的慣性力大于臨界橫向力時，走行輪一側穩定輪與軌道梁脫離，車輛的抗傾覆能力下降一半左右[11]。

設穩定輪預壓力為Fpre，臨界橫向力為Fccr，當一個穩定輪剛剛離開軌面時，式(6)中一個穩定輪的預壓力項消失，式(6)變為

(8)

根據式(8)，可求得穩定輪剛剛離開軌面時，構架產生橫移量和側滾角分別為

(9)

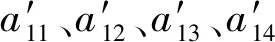
(10)

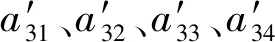
設穩定輪的徑向剛度為Kst，則穩定輪剛剛脫離軌道梁側表面時的橫移量臨界值為

yscr=Fpre/Kst

(11)

式中：Kst為穩定輪徑向剛度。

根據式(7)，有

Fpre/Kst=h5φbcr-ybcr

(12)

式中：φbcr為構架臨界側滾角；ybcr為構架臨界橫移量。

將式(9)、式(10)代入式(12)，得出

(13)

令

(14)

則

Fccr=n·Fpre

(15)

由式(15)可以看出：臨界橫向力與穩定輪和導向輪的預壓力成簡單的線性關系，臨界橫向力只取決于穩定輪和導向輪的預壓力以及車輛自身的參數；隨著穩定輪預壓力的增加，跨坐式單軌車輛能夠承受更大的臨界橫向力，抗側傾能力能夠更持續地保持在最大狀態。代入表1中的車輛參數，得到n=1.986 。

1.3 動力學仿真驗證

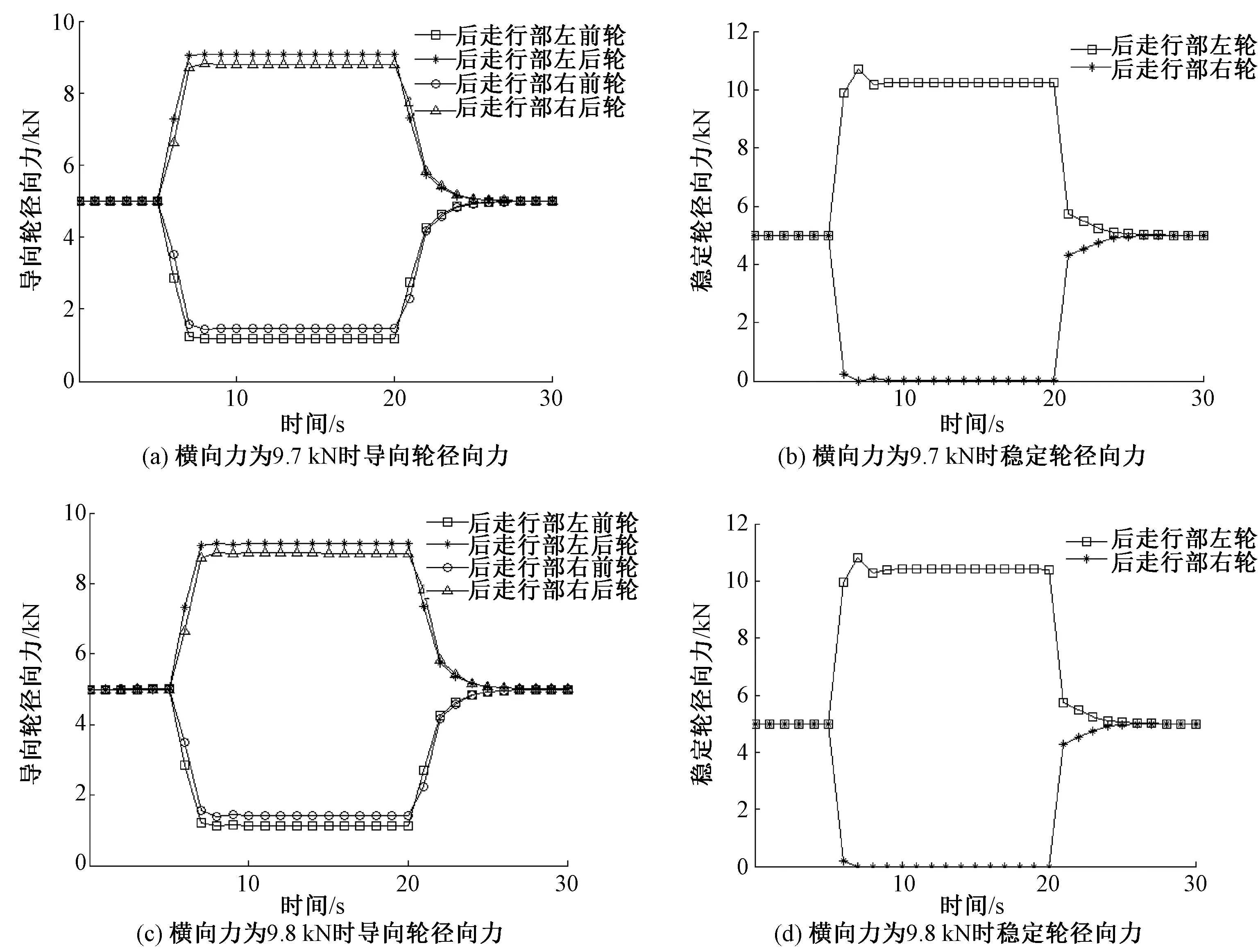
圖3 導向輪和穩定輪徑向力仿真結果

根據表1參數，基于多體動力學軟件UM建立跨坐式單軌車輛動力學模型，見圖2，以此來驗證公式的準確性。模型中，將橫向力緩慢施加在車體的質心。為盡量減小速度的影響，車輛以1 m/s的低速在直線上運行。

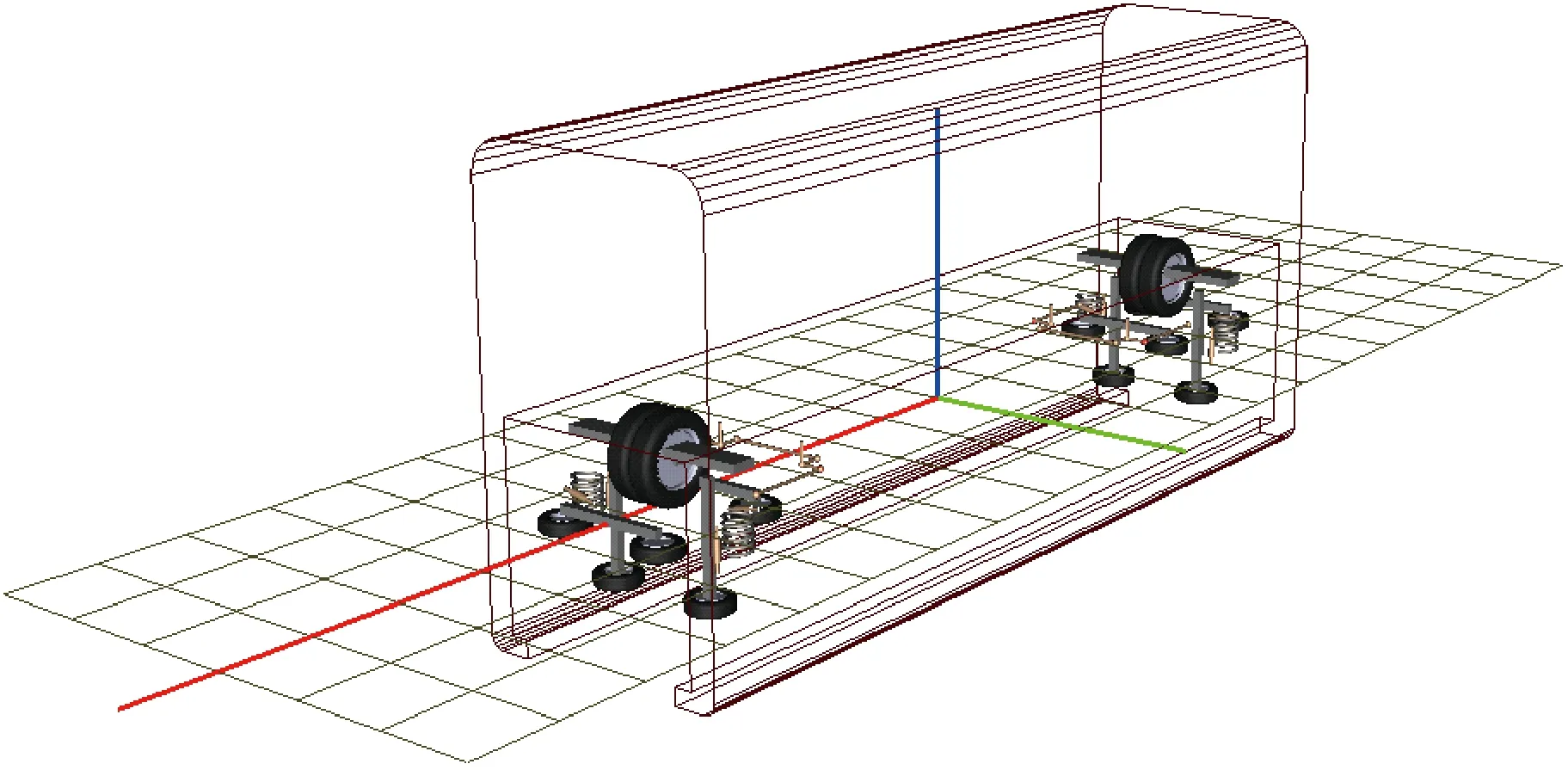
圖2 車輛UM動力學模型

設置導向輪和穩定輪初始預壓力為5 kN，且在車體質心上分別施加9.7 kN和9.8 kN的橫向力，可以仿真得到導向輪和穩定輪的徑向力，見圖3。從圖中可以看出：當車輛承受的橫向力為9.7 kN時，軌道外側的穩定輪和導向輪的徑向力數值都是大于零，表示此時的穩定輪和導向輪并沒有脫離軌道梁側表面；當車輛承受的橫向力為9.8 kN時，軌道外側導向輪的徑向力，而曲線外側穩定輪的徑向力減小為零，說明這時穩定輪已脫離軌道梁側表面，而導向輪沒有離開軌道梁側表面，依然處于接觸狀態。仿真結果說明，當穩定輪和導向輪的預壓力設置為5 kN時，臨界橫向力在9.7～ 9.8 kN之間，與式(15)所得值很接近。

表2為不同穩定輪預壓力作用下，臨界橫向力的仿真值和理論值。對比看出：UM軟件仿真值和根據式(15)得到的理論值非常接近，兩者的相對誤差在4.8%之內。

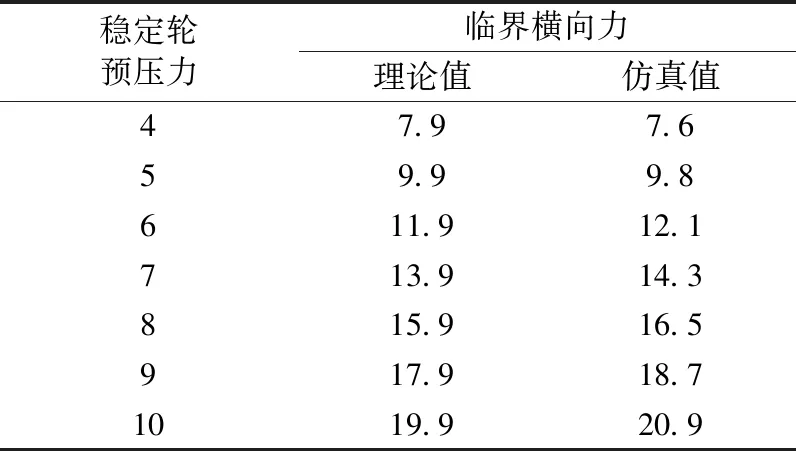
表2 臨界橫向力 kN

2 跨坐式單軌車輛的曲線限速

2.1 車體離心加速度與舒適度

國內外鐵路大量試驗和實踐證明，未平衡離心加速度ac影響乘客的生理感受，當ac<0.04g(g為重力加速度)時，乘客不會感受到離心加速度的存在；當ac=0.05g時，乘客可以感受到未平衡離心加速度的存在，但無不舒適的狀態；當ac=0.077g時，此時的離心加速度值在大多數乘客的可承受范圍之內；當ac=0.1g時，較少乘客能夠長時間承受這一未平衡離心加速度的影響。為確保車輛通過曲線路段時乘客的舒適性，國外鐵路標準通常要求ac≤0.05g[12]。

2.2 未平衡離心加速度的臨界值

跨坐式單軌車輛通過圓曲線路段時時，由于離心加速度的作用而向曲線外側傾斜，曲線內側穩定輪的載荷逐漸減小。隨著未平衡離心加速度的增大，車體向外傾斜的角度逐漸增大，曲線內側穩定輪的載荷逐漸減小。當未平衡離心加速度增至某一值時，曲線內側穩定輪恰好脫離軌面，稱這時未平衡離心加速度達到了臨界值。

當臨界橫向力由車輛的未平衡離心力引起時，則有

Fccr=mc·accr

(16)

式中：mc為車體質量；accr為未平衡離心加速度的臨界值。

根據式(15)和式(16)，則車體未平衡離心加速度臨界值與穩定輪預壓力的關系為

(17)

應用式(17)計算跨坐式單軌車輛在不同穩定輪預壓力下車體未平衡離心加速度臨界值，結果見表3。可以看出，預壓力越小，則車體未平衡離心加速度的臨界值就越小。當穩定輪預壓力給定時，如果通過曲線時車輛的速度過高，使得車輛的未平衡離心加速度超過臨界值accr，則穩定輪會離開軌面，其載荷變為零，則曲線通過的安全性不能保證[13-14]。因此，當穩定輪預壓力確定時，要對車輛的運行速度提出限制，使得車輛未平衡離心加速度小于臨界值accr，這樣才能保證單軌車輛在通過曲線時所有穩定輪和導向輪都和軌面接觸，確保曲線通過的安全性。

從保證行車安全的角度出發，穩定輪預壓力越大越好，這樣可以保證通過曲線時的未平衡離心加速度有較大的臨界值。但是從考慮旅客舒適度的需求出發，沒有必要將穩定輪預壓力設置的過高，只要使得與穩定輪預壓力相關的臨界未平衡橫向加速度值大于旅客舒適度所需要的值即可。穩定輪預壓力設置的過高，不僅增大構架穩定輪支撐梁的初始應力，對構架的結構強度不利，而且增加車輛的運行阻力，增加穩定輪的磨耗。根據式(17)，如果要求accr=0.05g，則對應穩定輪的臨界預壓力值取為5.19 kN。

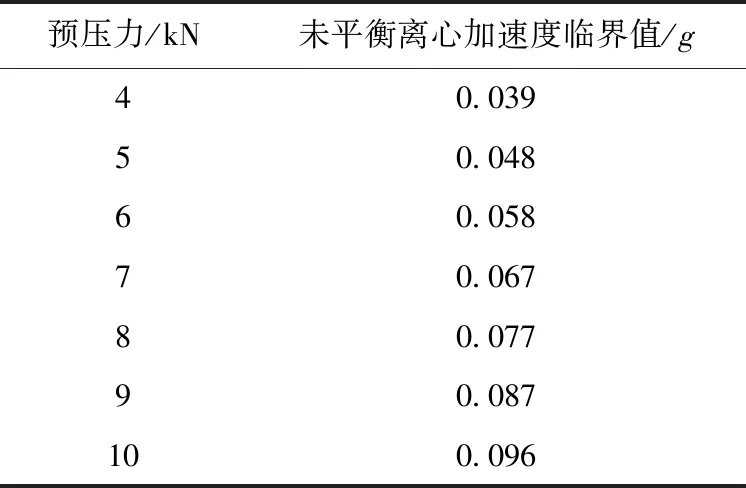
表3 未平衡離心加速度臨界值

2.3 軌道梁超高率的臨界值

當車輛停在有超高的軌道梁上時，因重力作用，車輛向線路內側傾斜，曲線外側穩定輪的徑向載荷減小。隨著軌道梁超高率的增大，車輛向內傾斜的角度也逐漸增大，曲線外側穩定輪的徑向載荷逐漸減小。當軌道梁超高率的增至某一值時，曲線外側的穩定輪恰好脫離軌道梁側面，稱這時軌道梁超高率達到了臨界值。

當車體臨界橫向力由軌道梁超高率引起時，則有

Fccr=mcgδ

(18)

式中：δ為軌道梁超高率。

根據式(15)，軌道梁超高率臨界值與穩定輪預壓力的關系為

(19)

從公式(19)可以看出，當穩定輪預壓力確定時，則對應一個軌道梁超高率臨界值，當軌道梁超高率的實際設置值小于該臨界值，則能夠保證車輛停在軌道梁上時所有穩定輪和導向輪都與軌道梁處于接觸狀態；反之，當軌道梁超高率確定時，可以反推出穩定輪所需要的預壓力臨界值，大于該臨界值，則能夠保證車輛停在軌道梁上時所有穩定輪和導向輪都與軌道梁處于接觸狀態。跨坐式單軌車輛在不同穩定輪預壓力下的軌道梁超高率臨界值見表4。

表4 軌道梁超高率臨界值

從提高曲線通過速度的角度考慮，需要設置較大的軌道梁超高率，但考慮到運營過程中可能出現曲線上停車的情況，根據車體離心加速度與舒適度的關系，軌道梁超高率不宜設置的過高。如果要求accr=0.05g，則對應軌道梁超高率為5%。

2.4 曲線限速

跨坐式單軌車輛通過坡度大、轉彎半徑小的曲線線路，與地鐵相比，其速度限制較多[15]。當車輛通過曲線時，如果速度大于均衡速度，則車輛向曲線外側傾斜并產生向外的未平衡加速度；如果通過曲線速度小于均衡速度，則車輛因軌道梁超高向曲線內側傾斜并產生向內的未平衡加速度；除考慮欠超高和過超高的情況，還要考慮車輛在梁上停車的工況[16]。為了保證旅客舒適性，需要對車輛通過曲線時的速度進行限制，使得未平衡離心加速度小于旅客舒適性要求的數值。同時還需考慮，當車輛通過欠超高曲線路段時，需要對車輛最高運行速度進行限制；當車輛通過過超高曲線路段時，需要對車輛最低運行速度進行限制。

單軌車輛以穩態工況通過圓曲線路段時，可知未平衡離心加速度ac與運行速度V、曲線路段半徑R以及軌道超高率δ之間的關系

(20)

將式(17)代入式(20)，得到最大和最小限制速度與穩定輪預壓力、軌道梁超高率以及曲線半徑的關系

(21)

從式(21)可以看出：穩定輪預壓力一定時，在相同半徑曲線，軌道梁超高率越大，則最高限制速度越大，但是在相同半徑曲線，軌道梁超高率越大，則最低限制速度也越大；軌道梁超高率一定時，在相同半徑曲線，穩定輪的預壓力越大，則最高限制速度越大，而最低限制速度越小。

設置穩定輪和導向輪的初始預壓力為7 kN，取不同的軌道梁超高率和曲線半徑，由式(21)可計算得到的單軌車輛通過曲線路段時的最高限制速度和最低限制速度，分別見表5和表6。當軌道梁超高率達到9%時，車輛在所有曲線上的最低限制速度都大于零，這意味著當車輛以小于最低限制速度通過曲線路段或在曲線路段上停車時，穩定輪都將脫離軌道梁，這將會影響車輛運行的安全性和穩定性。綜合考慮運行安全性和舒適度要求，當穩定輪和導向輪預壓力設置為7 kN時，軌道梁最大超高率設置為6%比較合適。

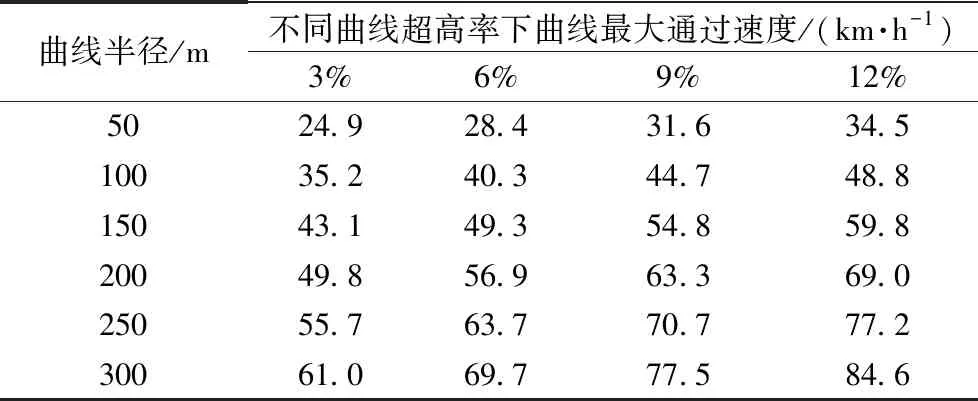
表5 曲線最大通過速度

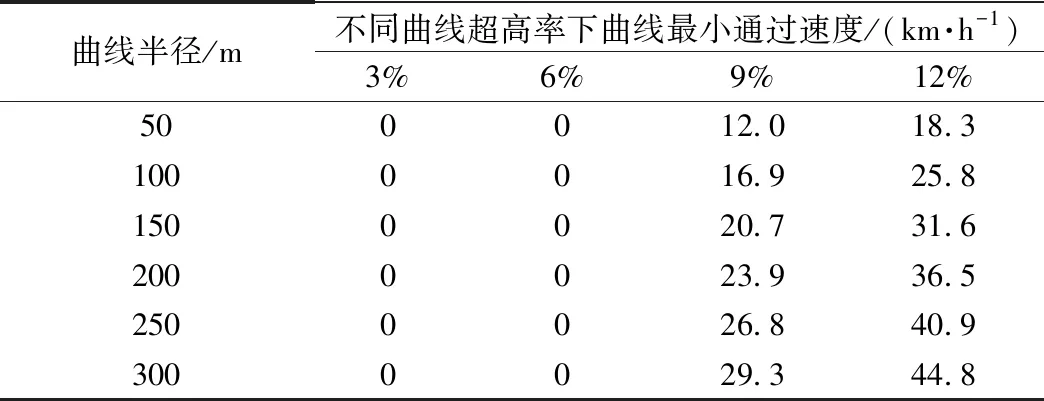
表6 曲線最小通過速率

3 結論

(1)在臨界橫向力和穩定輪預壓力關系的基礎上，從車輛乘坐舒適度的角度討論了穩定輪預壓力的合理取值問題。研究表明：從滿足旅客舒適度的需求出發，沒有必要將穩定輪預壓力設置的過高，只要使得與穩定輪預壓力相關的臨界橫向加速度值大于旅客舒適度所需要的值即可。

(2)推導了曲線通過最高限制速度和最低限制速度與穩定輪預壓力、軌道梁超高率以及曲線半徑之間的關系公式。為了保證通過曲線的旅客舒適性和運行安全性，跨坐式單軌車輛的軌道梁超高率不宜設置得過高，并且應對曲線通過的最高速度和最低速度進行限制。