動態想象，讓圖形在頭腦中生長

阮傳忠

摘要：

培養和發展學生的“空間觀念”，是小學數學“圖形與幾何”領域的核心目標和內容。空間觀念的培養主要依賴于學生的觀察與操作，然而學生在面對較為復雜的“圖形與幾何”問題時，往往思維混亂，“眼中有物，腦中無形”，導致空間想象過程不能順利進行，空間觀念很難向縱深發展。本文從“圖形與幾何”的概念、特征、聯系三個方面的教學現狀入手，探尋實際教學中如何有效激發學生的“動態想象”，發展學生的空間觀念。

關鍵詞：空間觀念動態想象

培養和發展學生的“空間觀念”，是小學數學“圖形與幾何”領域的核心目標和內容，也是學生適應高層次學習和發展所必備的關鍵能力。然而，在實際教學過程中，我們的學生在面對較為復雜的“圖形與幾何”問題時，往往思維單一，缺乏對問題本質的深刻理解和全面把握，“眼中有物，腦中無形”，導致空間想象、推理過程不能順利進行，數學思維很難向縱深發展。究其原因，主要是在教學時，老師習慣于讓學生在大量的動手操作中直接獲取表象，過分依賴于學生的觀察與操作，忽略了學生必要的想象和推理過程。《數學課程標準》指出，在“圖形與幾何”教學中，應注重學生在觀察、操作、想象、推理等學習活動中，發展學生的空間觀念。所以，筆者結合“圖形與幾何”教學實踐，談談如何從動手轉向動腦，進而實現“腦手并用”，促使學生從單一的靜態表象展開豐富的動態想象，讓圖形在頭腦中生長，發展學生的空間觀念。

一、建構圖形概念時進行動態想象

在圖形與幾何的教學中，教師往往將目光聚焦在單個課時的圖形概念上，忽視單元或學段知識之間的內在整體性聯系;關注更多的是靜止狀態下的數學知識，忽視了基本圖形之間的動態轉化;過于關注圖形表象特征的全面掌握，忽視對圖形結構本質屬性的把握。因此，在建構圖形概念時，教師要適時啟發學生在頭腦中展開積極的動態想象，在動態想象中激活兒童思維的“沸點”，讓其經歷圖形的運動、變化與生成，進而感悟基本圖形之間的內在聯系，從而幫助學生有效把握基本圖形概念的本質屬性。

例如，在教學“長方體和正方體的認識”時，先對“一條線段經由垂直方向作平移，形成一個長方形，進而再將這個長方形沿與所在平面相垂直的方向平移，即可獲得一個長方體”展開有效的“動態想象”，感悟到空間形體可被看成是由較簡單的圖形經由運動變化生成的思想。在學生初步認識長方體特征之后，通過相交于一個頂點的三條棱，讓學生在頭腦中還原出這個長方體的表象。這正是從思維的逆向角度對學生所學知識的有效重構。與此同時，教學中教師還不忘讓學生說出還原過程中各個面與對應棱之間的關系，從而進一步加深學生對長方體面、棱、體三者之間關系的深刻理解，使其在邊畫邊說的過程中，手腦并用，強化認知基礎，抓住長方體和正方體結構特征的本質屬性。通過這樣的動態想象，學生眼中不僅有“物”，腦中更加有“形”，經歷的是想象，留下的是思想。

二、突破知覺障礙時進行動態想象

我們知道，“圖形與幾何”領域有很多知識內容的教學，是需要借助于學生的直觀操作去加以驗證的。但有時這種“靜態”操作反而給學生的認知帶來障礙，不利于學生對知識的正確理解。例如，在教學“三角形三邊關系”時，對于其中“兩邊之和等于第三邊”的情況，學生在動手操作后，常常會產生視覺錯覺，認為也能圍成一個三角形。究其原因，主要是直觀的學具本身有寬度，再加上學生心里想圍成一個三角形，所以在操作中左邊挪一點、右邊挪一點，再將上面兩根小棒慢慢往下壓，最后兩根小棒的端點碰在了一起。僅從視覺上判斷，很難讓學生不相信圍不成一個三角形。盡管有的老師對實驗材料和方法進行了有效的改進，并大大減少了操作的誤差，但還是很難讓人信服。因此，如何突破“靜態”操作中的視覺誤差所產生的知覺障礙，就需要適時地展開“動態想象”。將頭腦中已有的“兩邊之和等于第三邊”的重合表象，在語言的描述下進行旋轉變形——兩條短邊在上拱的過程中缺口會越來越大，激活學生的數理邏輯經驗，想象出運動變化的過程和結果，從而在頭腦中完成思維實驗，突破教學難點，促進學生空間觀念向縱深發展。

“三角形三邊關系”教學片斷：

課件演示（如圖1）：6厘米和4厘米兩根小棒正好和10厘米的小棒重合在一起。

圖1

師：這是三角形嗎？

生：（齊）不是。三根小棒重合在一起，是一條線，而且中間沒有空隙，需要將兩根短棒的交點（公共頂點）往上拉。

師：想象一下，如果固定兩根短棒的一端，使其往上慢慢移動，這時它們的公共端點會發生怎樣的變化？

生：中間會分開，向左右兩邊慢慢打開。

師根據學生的描述相機動態演示（如圖2）：兩個端點開始時剛好連在一起，這時只要將它們向上移動一點點，它們就會一左一右地分開了，這樣還是三角形嗎？

圖2

生：不是。

師：所以用10厘米、6厘米、4厘米的三根小棒——

生：（齊）不能圍成三角形。

三、溝通圖形聯系時進行動態想象

對于平面圖形，教材在編排時突出了“轉化”思想的滲透，然而在實際計算時學生很容易對相關圖形的面積公式產生記憶混淆。分析原因，筆者以為是教材過于強調對平行四邊形面積的“依賴”，忽視了平面圖形之間的內在邏輯聯系，缺乏從整體上溝通聯系。因此，通過適當、合理的“動態想象”，幫助學生有效溝通平面圖形面積之間的內在關聯，形成知識網絡結構，就顯得非常重要。

例如，在學習了平面圖形的面積之后，我們可以安排這樣的整合練習：給出高和面積一定的梯形，讓學生對符合已知條件的梯形展開有效的“動態想象”，從而感悟梯形上、下底之間的關系。在不同梯形的變化之中感悟極限思想，體會不同平面圖形面積公式之間的相通之處，從而突破因教材編排設計而產生的邏輯線索的束縛，形成整體性認知結構，進而感悟平面圖形之間的等積變形思想和方法，理清知識脈絡，形成知識網絡。

“多邊形的面積”教學片斷：

你能在一組平行線（如圖3）之間畫出高為5厘米，面積為20平方厘米的梯形嗎？（注：每一小方格邊長為1?cm）

圖3

1.生獨立思考，在格子紙上畫一畫。

2.組內交流。

3.作品展示、匯報交流。

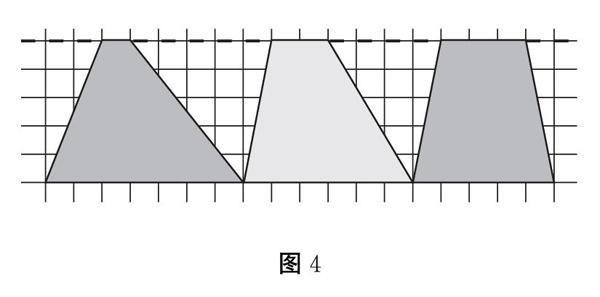
教師課件出示不同梯形（如圖4），問：請仔細觀察這些上底和下底分別為1和7、2和6、3和5的梯形，你有什么發現？

圖4

4.小組交流。

它們的上底和下底相加的和都等于8。

（發現梯形等積變形的本質：上、下底之和不變）

5.“動態想象”，溝通聯系。

師：從右往左看，如果梯形的上底繼續縮短，想一想會怎么變、變成怎樣的圖形。

生：越來越接近三角形。

師：大家有沒有聽明白她的意思？請你上臺演示給大家看看。

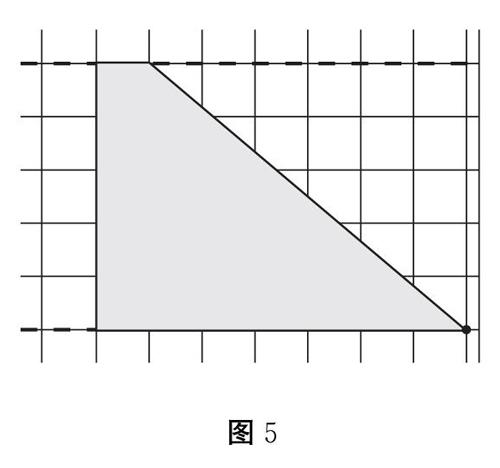
生操作演示（如圖5）

圖5

師：在什么情況下，梯形會變成三角形？

生：當梯形的上底越來越短，長度為0時，就會變成三角形，此時的下底剛好等于8。

師：這時怎么計算三角形的面積？

生：（0+8）×5÷2。

師：也就是說，梯形的面積公式還可以用來計算三角形的面積。

[板書：當上底=0時，三角形面積=（上底+下底）×高÷2]

6.實時整合，建構網絡。

師（指著圖4）：從左往右看，當梯形的上底不斷變長，下底也就會不斷變短，想象一下，梯形又會發生什么變化呢？

生：噢！會變成平行四邊形。

師：那么，平行四邊形的面積是不是也可以用梯形面積公式來計算呢？

教師相機板書，溝通平面圖形的面積關系。

總之，空間觀念看不見、摸不著，是一種印象，更是一種能力，具有一定的抽象性。我們在“圖形與幾何”教學中，既要處理好“動態想象”與“動手操作”之間的辯證關系，避免學生操作活動的隨意性和虛假性，還要讓學生有想象的材料、想象的平臺、想象的時間和想象的方法。如此堅持，學生的空間觀念才有持續和深入的可能，學生的思維品質才能得到有效的提升。

參考文獻：

[1]董雪云.在“動態想象”中發展兒童的空間觀念[J].江西教育，2017（12）.

[2]江莉莉.讓“動態想象”潤澤小學數學課堂[J].小學教學研究，2012（6）.

責任編輯：黃大燦