四類易錯問題的糾錯
武增明
(云南省玉溪第一中學 653100)
一、易錯問題

問題2若關于x的不等式0≤x2+ax+5≤4恰有一個實數解,求實數a的值.
問題3已知函數f(x)=log2019(x2-ax+65)的值域為R,求實數a的取值范圍.
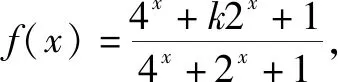
二、問題糾錯

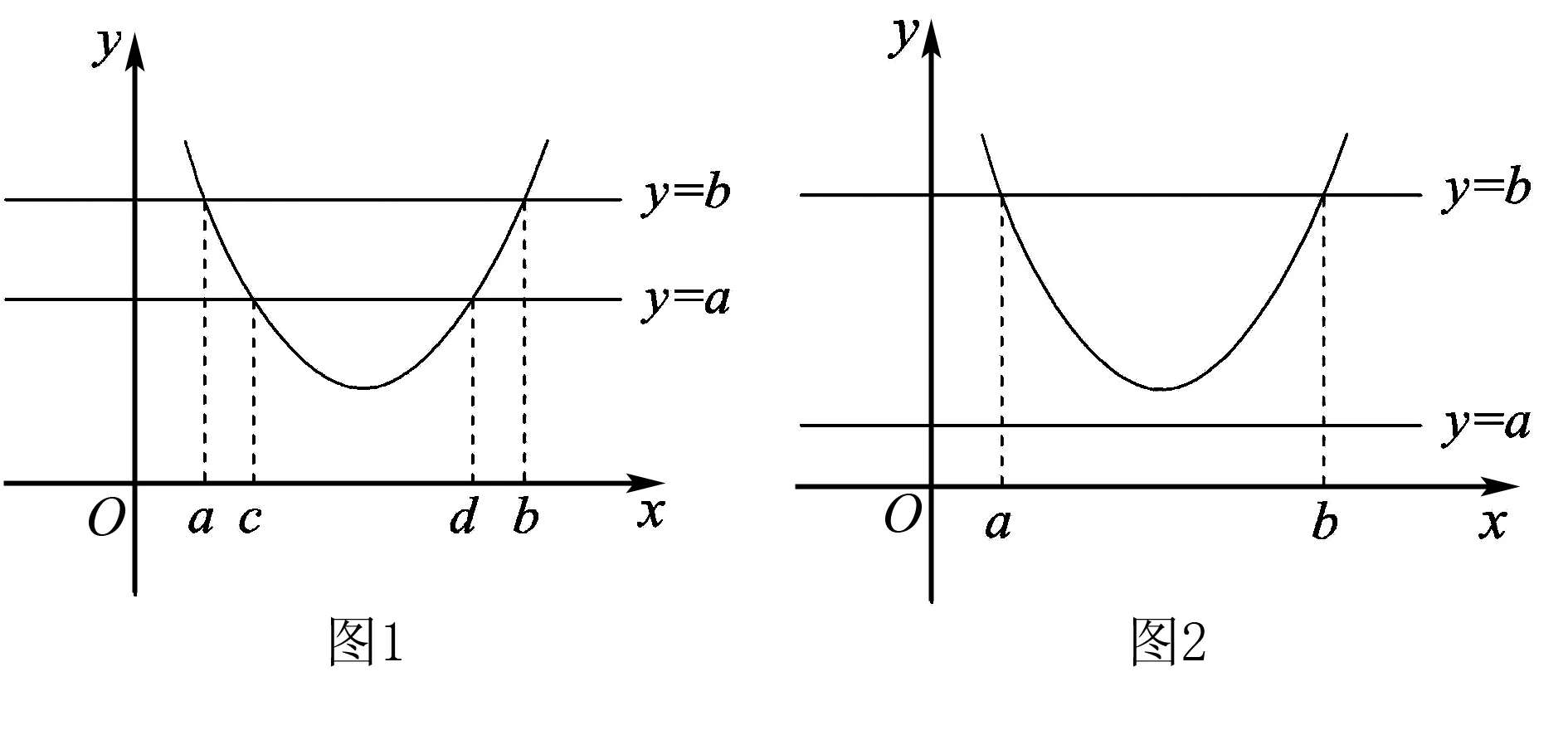
由上述解答,反面探究,我們可知:
(1)若關于x的不等式m
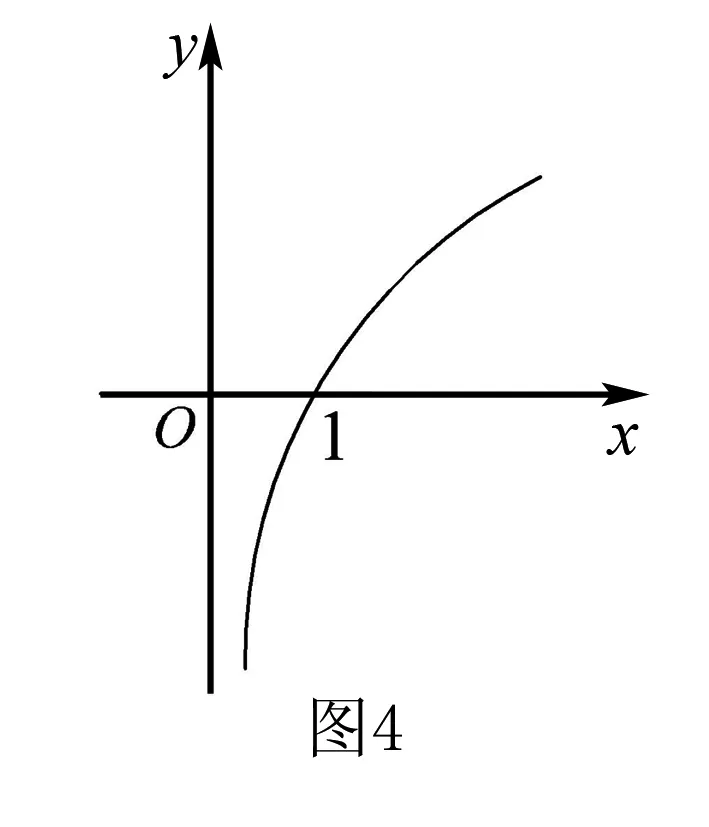
(2)若關于x的不等式m 問題2解答 因為y=x2+ax+5是開口向上的拋物線,如果此拋物線的頂點在直線y=4的下方(如圖3),則原不等式有無窮多解.如果頂點在y=4的上方(如圖3),則原不等式無解. 當且僅當此拋物線的頂點落在直線y=4上(如圖3)時(即取原不等式右端等號時),原不等式恰有一個解. 另解由上述分析知,關于x的不等式x2+ax+5≥0對一切x∈R恒成立,從而關于x的不等式x2+ax+5≤4恰有一個實數解,于是,關于x的一元二次方程x2+ax+5=4有兩個相等實數解,所以,Δ=a2-4=0,解得a=±2. 由上述解答,反面探究,我們將會發現: (1)把問題2不等式左邊的“0”改為區間(-∞,4)內的任意一個確定的實數,如“1”或“2”或“3”或“3.1”,并不影響這個問題的解答思路和結果. (2)問題1和問題2本質上是同一類題目. 由上述解答,反面探究,我們可知: (1)若關于x的不等式m≤ax2+bx+c≤n(a>0)恰有一個實根,則關于x的一元二次方程ax2+bx+c=n必有兩個相等實根. (2)若關于x的不等式m≤ax2+bx+c≤n(a<0)恰有一個實根,則關于x的一元二次方程ax2+bx+c=m必有兩個相等實根. 在這里,關鍵是要理解清楚以下兩個問題. 第一個問題是要使函數f(x)的值域為R, 為什么應使對數的真數x2-ax+65要取盡所有正實數?因為函數h(x)=log2019x的值域為R,當且僅當對數的真數x要取盡所有正實數,如圖4所示,否則,如取2≤x≤4,則h(x)的值域為[log20192,log20194]. 由上述問題1、問題2、問題3的解答,反面探究,我們將會看到問題1、問題2、問題3的解答思維方法都是逆向思維,從反面入手去探究解決問題的突破口. 問題4解答因為對任意的實數x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,所以2f(x)min>f(x)max. 若k-1=0,即k=1,則y=1,此時滿足不等式f(x1)+f(x2)>f(x3). 許多同學很難想到:(1)若函數y=f(x)在區間D上單調,且對任意的x1,x2,x3∈D,不等式f(x1)+f(x2)>f(x3)恒成立,則f(x)min+f(x)min>f(x)max,即2f(x)min>f(x)max.(2)若函數y=f(x)在區間D上單調,且2f(x)min>f(x)max,則對任意的x1,x2,x3∈D,不等式f(x1)+f(x2)>f(x3)恒成立. 對于問題2這樣關于“不等式m≤ax2+bx+c≤n(a>0)恰有一個實根”的問題,解題時關鍵是要理解:ax2+bx+c≥m恒成立,從而就可以知道問題的本質是,不等式ax2+bx+c≤n恰有一個實根,故而問題破解. 對于問題3這樣關于“函數f(x)=logag(x)(a>0,且a≠1)的值域為R”的問題,解題時關鍵是要理解:函數g(x)的取值要取盡所有正實數,從而問題得解. 對于問題4這樣關于“對任意的實數x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立”的問題,解題時關鍵是要理解:2f(x)min>f(x)max,從而就可以知道問題的本質是,求函數y=f(x)的最值(值域),故而問題獲解. 1.問題1變式 2.問題2變式 (1)a為何值時,不等式0≤x2+ax+5≤4恰有一個實解.(a=±2) (2)若不等式0≤x2-ax+a≤1恰有一解,求a的值.(a=2) (3)已知不等式2≤x2+px+10≤6恰有一個解,求p的值.(p=±4) 3.問題3變式 (2)已知函數f(x)=lg(ax2+2x+1)的值域為R,求實數a的取值范圍.(0≤a≤1) (4)若函數f(x)=log2019(x2-ax+65)的值域為非負實數,那么a的取值是____.(a=±16) 4.問題4變式 (2)已知函數f(x)=2x+1+a,若對任意的實數x1,x2,x3,不等式f(x2)+f(x3)>f(x1)恒成立,則實數a的取值范圍是____.(a≥6) 以上四個問題變式解答從略,各題后面括號內為答案. 學生解題出現錯誤是很自然的現象,問題是學生為什么對同一個問題或同一類問題一而再、再而三地重復同樣錯誤,糾錯為什么這么難?對此問題,筆者認為,學生對同一個問題或同一類問題多次重復同樣的錯誤,是教師在教學中的不足.我們常常會聽到這樣的責怪聲:“這個問題我已經講過多少遍了,現在還有不少學生出錯.唉!沒有辦法了.”真的沒有辦法了嗎?到底是誰的錯?對此問題,我們應該靜下心來認真地作一些反思,反思是否使學生對問題知其然、知其所以然、何由以知其所以然.知其然、知其所以然、何由以知其所以然是理解數學知識的三重境界,是數學教師專業化發展的基石,是數學教學質量的根本保證,也是衡量學生是否理解和掌握數學知識的發生、形成、發展過程的重要指標. 人教A版《普通高中課程標準實驗教科書·數學》的“主編寄語”中寫道:數學概念、數學方法與數學思想的起源與發展都是自然的.如果有人感到某個概念不自然,是強加于人的,那么只要想一下它的背景、它的形成過程、它的應用,以及它與其他概念的聯系,就會發現它實際上是水到渠成、渾然天成的產物,不僅合情合理,甚至很有人情味 .也就是說,糾錯應該是自然的、水到渠成的、合情合理的.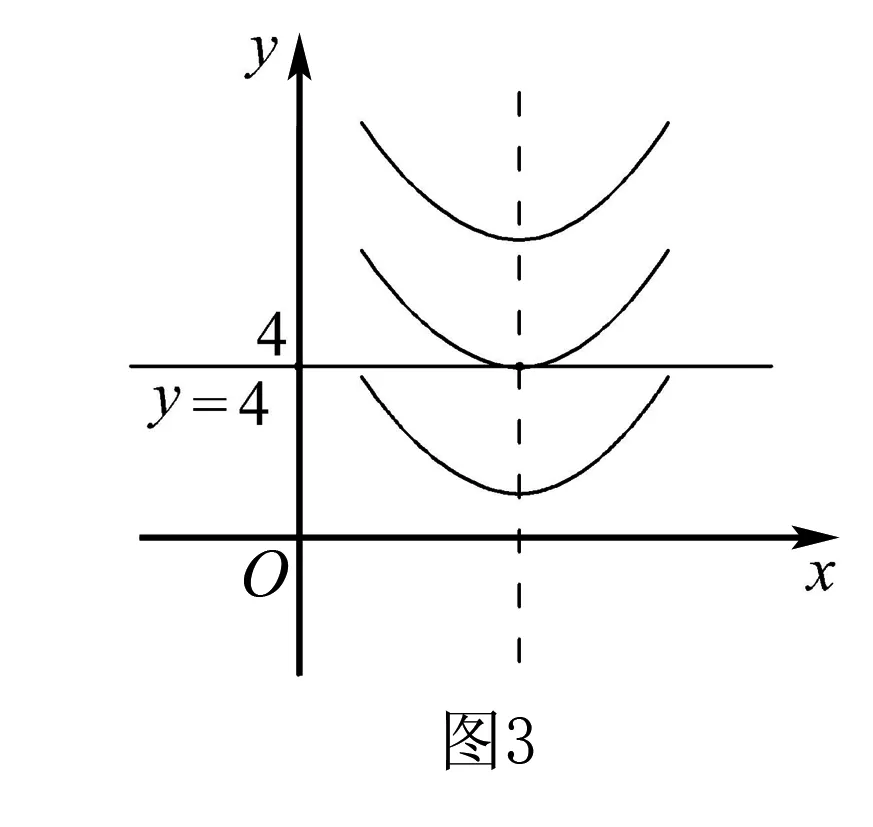
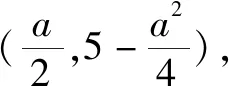
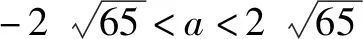


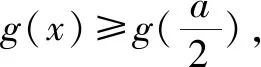
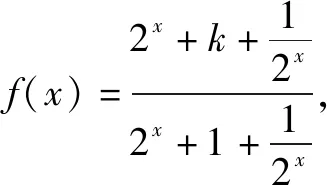
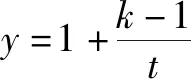
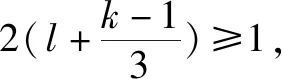

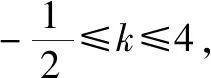
三、問題關鍵
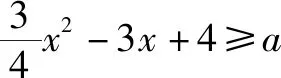
四、問題變式
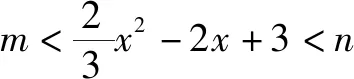
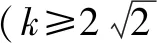
五、糾錯反思

