理想氣體狀態方程微分式及其應用

許冬保

(江西省九江第一中學 332000)

一、理想氣體狀態方程微分式

設某理想氣體在溫度為T時，壓強及體積分別為p、V.由克拉珀龍方程知pV=nRT，式中n為摩爾數，R為摩爾氣體常量.

假設氣體的質量不變(或n不變).對該式兩邊進行微分運算，可以得到d(pV)=nRdT，即pdV+Vdp=nRdT

下面對該式作些討論.

1. 查理定律微分式

2.蓋—呂薩克定律微分式

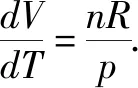
3.玻意耳定律微分式

4.體積功的微分式

假設氣體發生準靜態過程，且氣體的壓強保持不變，當體積變化dV時，因體積變化所對應的元功為dW=pdV.結合克拉珀龍方程微分式，得到dW=nRdT.

二、應用

1.水銀柱移動問題的分析

例1 如圖1所示，兩容器用水平細管相連，容器內裝有溫度均為T的同種理想氣體.若管中有一小段水銀柱將A、B兩部分氣體隔開，現使A、B同時升高溫度，若A升高到T+ΔTA，B升高到T+ΔTB，已知VA=2VB，欲使水銀柱向右移動，則 ( ).

C.ΔTA<ΔTBD.ΔTA>ΔTB

分析A、B兩部分氣體溫度升高時，兩部分氣體的體積不變，假設壓強的增加量分別為ΔpA、ΔpB.由查理定律的微分式，有

欲使水銀柱向右移動，則dpA>dpB，即dTA>dTB或ΔTA>ΔTB.選項D正確.

點評水銀柱移動問題涉及氣體壓強、體積和溫度三個量的變化，常用假設法進行分析.假設溫度變化時水銀柱不動，通過比較水銀柱兩側氣體壓強的增量，來判斷水銀柱移動的方向.或反過來由水銀柱移動方向來判斷溫度變化的情況.解題方法上也常選擇p-T圖像進行直觀分析.

例2 如圖2所示，三根粗細均勻的細玻璃管，中間均用一段水銀柱封住溫度相同的空氣柱，且V1=V2>V3，h1

A.丙管 B.甲管和乙管

C.乙管和丙管 D.三管上移一樣多

例3 如……