函數零點問題及解題策略

李 偉

(遼寧省鞍山市第三中學 114000)

函數零點是高考重點考查的問題，函數零點與相關知識的綜合更是高考壓軸題時常出現的題目，所以搞清零點的概念，研究零點問題的題型，探究零點問題解題思考就顯得十分重要.下面通過一些示例說明零點問題的題型和解決零點問題的思考.

一、零點唯一性問題

從題型角度講，一是判斷、證明有唯一零點；二是已知零點唯一，求參數、解決不等式等問題.解題思考：函數曲線與x軸只有一個交點.由此引出兩種思考：曲線單調性僅一次穿越x軸；或曲線與x軸相切(切于極值點).

例1 (2018年全國二卷 理第21題)已知函數f(x)=ex-ax2．

(1)若a=1，證明：當x≥0時，f(x)≥1；

(2)若f(x)在(0,+)只有一個零點，求a．

略解問題(1)略.

問題(2)，f′(x)=ex-2ax；f″(x)=ex-2a.

a≤0時，f(x)=ex-ax2>0，所以，不合題意.

a>0時，

設函數h(x)=1-ax2e-x,f(x)在(0,+∞)只有一個零點當且僅當h(x)在(0,+∞)只有一個零點．h′(x)=ax(x-2)e-x．

當x∈(0,2)時，h′(x)<0;當x∈(2,+∞)時，h′(x)>0.

所以h(x)在(0,2)單調遞減，在(2,+∞)單調遞增．

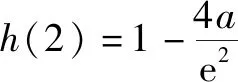
二、零點與方程的根

函數的零點就是該函數對應方程的根，從這個意義上講，可以從解方程角度求解零點問題，也可以從函數圖象與x軸交點，即數形結合角度求解零點問題.

例2 (2013年全國二卷 理第10題)已知函數f(x)=x3+ax2+bx+c，下列結論中錯誤的是( )．

A．?x0∈R,f(x0)=0

B．函數y=f(x)的圖象是中心對稱圖形

C．若x0是f(x)的極小值點，則f(x)在區間(-,x0)單調遞減

D．若x0是f(x)的極值點，則f′(x0)=0.

略解若x0是f(x)的極小值點，則x0是方程f′(x)=3x2+2ax+b=0的一個實根，設另一實根為x1，則x1是f(x)的極大值點.由已知得f(x)在(-,x1)是增函數，在(x1,x0)是減函數，在(x0,+)是增函數，所以答案選C.

另：此題用淘汰法做更簡捷.

三、零點存在性問題

零點的存在性問題有別于零點個數問題，此類問題核心是有，多少并不重要.所以，可以從單調性、解方程、數形結合、極值點、零點化簡代換等各層面來思考問題的解決.

(1)討論f(x)的單調性，并證明f(x)有且僅有兩個零點;

(2)設x0為f(x)的一個零點，證明曲線y=lnx在點A(x0,lnx0)處的切線也是曲線y=ex的切線.

略解(1)f(x)在(0,1)、(1,+)上為增函數.由于f(x)在(0,1)上為連續的增函數，所以，f(x)在(0,1)上只有一個零點.同理f(x)在(1,+)只有一個零點，因此f(x)有且僅有兩個零點.

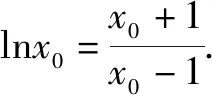
四、零點與極值點問題

零點與極值點問題的兩個方面：函數極值點就是其導數的零點，函數圖象與x軸相切于極值點則極值點就是函數零點.由此，我們可以從零點角度思考極值點，也可從極值點角度思考零點，所以處理零點問題的思考也可以借鑒到極值點問題上來.

例4 (2017年全國二卷 理第11題)若x=-2是函數f(x)=(x2+ax-1)ex-1的極值點，則f(x)的極小值為( ).

A.-1 B.-2e3C.5e3D.1

略解因為x=-2是函數f(x)=(x2+ax-1)ex-1的極值點，所以x=-2是導數f′(x)=[x2+(2+a)x+a-1]ex-1的零點.所以，f′(-2)=0,即(-2)2-2×(a+2)+a-1=0，解之，a=-1.

又由f′(x)=(2x-1)ex-1+(x2-x-1)ex-1=0，得零點x=-2，x=1.而x<-2時，f(x)為增函數;-21時，f(x)為增函數.所以，極小值為f(1)=-1.選A.

例5 (2017年 全國一卷 第21題)已知函數f(x)=ae2x+(a-2)ex-x.

(1)討論f(x)的單調性；

(2)若f(x)有兩個零點，求a的取值范圍.

略解(1)由已知得f′(x)=2ae2x+(a-2)ex-1=(aex-1)(ex+1).

①當a≤0時，f′(x)=(aex-1)(ex+1)≤0恒成立，故而函數恒遞減.

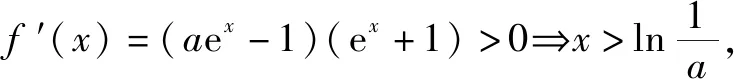
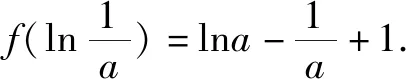
五、借助零點解(證明)某些特殊不等式

借助零點與函數的單調性可以解決特殊不等式(>0,<0)的求解問題.一般做法研究單調性、數形結合確定曲線形態，用觀察法、解方程等找零點等，特別是超越不等式用此解決的比較多.

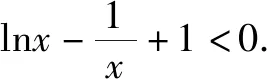
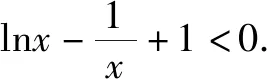
六、已知零點求參數問題

已知零點求參數問題解法，一是借助數形結合；二是借助求極值(最值)的方法.這些求解方法如何運用關鍵還是要具體問題具體分析.

略解x≤0時，g′(x)=ex+1>0，所以，g(x)在(-,0]是增函數.x>0時，所以g(x)在(0,+)是增函數.由已知方程g(x)=f(x)+x+a=0有兩根，即f(x)=-x-a有兩根，由數形結合知a≥-1.

例8 (2017年全國三卷 第11題)已知函數f(x)=x2-2x+a(ex-1+e-x+1)有唯一零點，則a=( ).

略解設t=x-1，則原命題等價于f(t)=t2-1+a(et+e-t)有唯一零點.

例9 (2014年全國一卷 理第11題)已知函數f(x)=ax3-3x2+1，若f(x)存在唯一的零點x0，且x0>0，則a的取值范圍為( ).

略解a=0時，f(x)=-3x2+1有兩個零點.不合題意.

a<0時，同理，解得a<-2， 所以選B.

七、判斷零點個數問題

討論零點個數與判斷零點存在的性的區別是要指出何時有無零點、幾個零點，解決問題的方法是一樣的.

(1)當a為何值時，x軸為曲線y=f(x) 的切線；

(2)用min{m,n} 表示m，n中的最小值，設函數h(x)=min{f(x),g(x)}(x>0),討論h(x)零點的個數.

對于問題(2)，注意到函數定義域是x>0.由于f′(x)=3x2+a，a≥0時，f(x)在(0,+)是增函數，且顯然g(x)=-lnx在(0,+)有一個零點.而x≥1時，f(x)>g(x)，所以此時只有一個零點.

a<0時，類似上述討論即可解決.

八、代換法解決零點問題

代換的目的是簡化題目，通過代換分解解題步驟，層層剝離，達到降低難度的目的.另外此種方法也可用來解決復合函數的零點問題.

略解由于函數y=f(x)是定義域R上的偶函數，所以f(x)在(-,-2)和(0,2)上遞增，在(-2,0)和(2,+)上遞減.

設t=f(x)，則方程[f(x)]2+af(x)+b=0轉化為：t2+at+b=0.

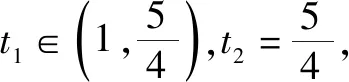
九、借助零點進行化簡代換

函數f(x)的零點x0即滿足f(x0)=0，借助零點進行化簡代換的含義就是在解題過程中，如果x0是函數f(x)的零點，則可以思考是否需要借助f(x0)整體與0的互相代換，或其式子(變式)f(x0)與0的互相代換去解決問題.

例12 (2016年 全國一卷 理第21題)已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點.

(1)求a的取值范圍；

(2)設x1、x2是f(x)的兩個零點，證明：x1+x2<2．

略解(1)a=0時，f(x)=(x-2)ex，所以，函數無兩個零點.

a>0時f′(x)=(x-1)(ex+2a).x=1是f(x)極小值點，且f(1)=-e<0，顯然此時f(x)有兩個極值點.

(2)不妨設x1

由于函數f(x)在x∈(-,1)上為減函數，

所以要證明x1+x2<2，即x1<2-x2.由于函數f(x)在x∈(-,1)上為減函數，只需證明f(x1)>f(2-x2).注意到x1是零點，有f(x1)=0，即只需證0>f(2-x2).注意到此時有f(x2)=(x2-2)ex2+a(x2-1)2=0，即只需證明：f(2-x2)=-x2e2-x2-a<0,x2>1.

構造函數g(x)=-xe2-x-a(1-x)2(x>1)，顯然可證g(x)<0.所以有x1+x2<2

例13 (2019年全國一卷 第20題)已知函數f(x)=sinx-ln(1+x)，f′(x)為f(x)導函數，證明：

(2)f(x)有且僅有2個零點.

(2)函數定義域為x>-1.

所以，綜合上述知f(x)有且僅有2個零點.

以上是就函數零點題型、解題思考進行一些探索，給出了一些解法，由于解方程和簡單數形結合處理問題比較簡單，限于篇幅沒有陳述，請讀者自行查閱教材.