峰回路轉難有因 順藤摸瓜終得果
——對2018年高考(Ⅱ)壓軸題的解法剖析

袁 琳

(甘肅省通渭縣第二中學 743300)

一、例題及解析

已知函數f(x)=ex-ax2，

(1)若a=1，證明：當x≥0時，f(x)≥1；

(2)若f(x)在(0,+)只有一個零點，求a.

1.高考標準答案的解題過程

(1)當a=1時，f(x)≥1等價于(x2+1)e-x-1≤0，

設g(x)=(x2+1)e-x-1，則g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x，

當x≠1時，g′(x)<0，∴g(x)在[0,+)上單調遞減，而g(0)=0，故當x≥0時，g(x)≤0，即f(x)≥1.

(2)設函數h(x)=1-ax2e-x，

f(x)在(0,+)只有一個零點當且僅當h(x)在(0,+)只有一個零點，

①當a≤0時，h(x)>0，h(x)沒有零點，

②當a>0時，h′(x)=ax(x-2)e-x，

當x∈(0,2)時，h′(x)<0；當x∈(2,+)時，h′(x)>0，

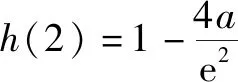
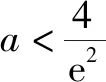
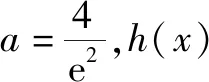
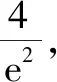
故h(x)在(2,4a)有一個零點，因此h(x)在(0,+)有兩個零點，

綜上，f(x)在(0,+)有一個零點時，

2.對標準解答的兩點質疑

(1)親臨考場，考生對“巧的變形”能否想到？一般地，當給定的條件式較復雜或未知時，易想到化歸與轉化思想，化復雜為簡單，化未知為已知.此題條件式從結構與形式上，已很簡化、明了，而標準答案的變形式比原式的更復雜，或許考生對此變形難有突破.

(2)解答(1)與(2)的思維能否有效地銜接上？標準答案的(1)與(2)的解題均以“先變后建”為入口，如果(1)的解答不按標準答案來解答，那么(2)的解答更難與標準答案來對接了.筆者對該題做了深入鉆研，提出以下常規解法：

①當a=1時，不妨設g(x)=ex-2x，則g′(x)=ex-2.

∵在[0,ln2)上，g′(x)<0，在(ln2,+)上，g′(x)>0，

∴g(x)在[0,ln2)上單調遞減，在(ln2,+)上單調遞增，

∴g(x)≥g(ln2)=2(1-ln2)>0，即f′(x)>0，∴f(x)在[0,+)上單調遞增，∴f(x)≥f(0)=1，即f(x)≥1.

②f′(x)=ex-2ax，令g(x)=ex-2ax，則g′(x)=ex-2a.

(ⅰ)當a≤0時，g′(x)>0，∴g(x)在(0,+)是單調遞增，

∴g(x)>g(0)=1，即f′(x)>0，∴f(x)在(0,+)是單調遞增，

∴f(x)>f(0)=1>0，故函數f(x)在(0,+)上沒有零點，不合題意.

(ⅱ)當a>0時，令g′(x)=0，則x=ln2a.

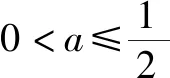
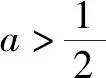
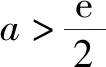
且若x→0，則g(x)→1；若x→+，則g(x)→+.

不妨設x1,x2是方程g(x)=0的兩實數根，

則在(0,x1)上g(x)>0；在(x1,x2)上g(x)<0；在(x2,+)上g(x)>0，

∴f(x)在(0,x1)是單調遞增；f(x)在(x1,x2)是單調遞減；f(x)在(x2,+)是單調遞增.∵f(0)=1，∴f(x)的零點只有在x2處取得，令①

又g(x)=ex2-2ax2=0 ②

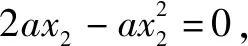
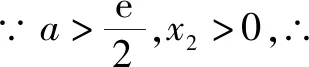
二、以零點的概念為據對(2)做進一步的探究

1.分離參變量法

令f(x)=0，則ex-ax2=0，∵x∈(0,+)，令(0,+)，則在(0,2)，h′(x)<0；在(2,+)，h′(x)>0，∴h(x)在(0,2)上單調遞減；在(2,+)上單調遞增，又若x→0，則h(x)→+；若x→+，則h(x)→+.事實上，當x→0時，的結構型，顯然h(x)→+；而當x→+時，的結構型，根據教材中所學知識：當x為較大值時，指數函數y=ex的增長遠比y=x2的增長大，得知.

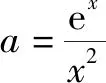
2.數形結合法

令f(x)=0，則ex=ax2.

令t(x)=ex,x∈(0,+),k(x)=ax2,x∈(0,+).

在同一直角坐標系下，畫出兩個函數的圖象：

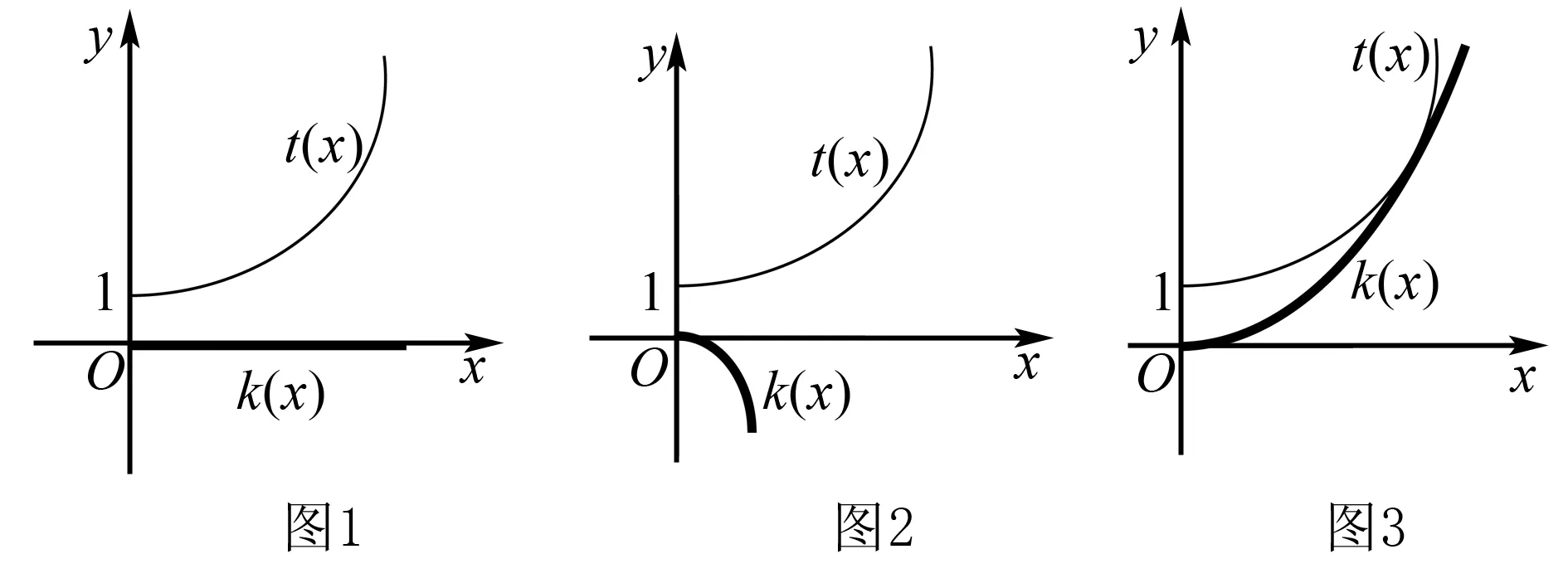
1.當a=0時，如圖1，因兩個函數的圖象沒有交點，故f(x)沒零點，不合題意.

2.當a<0時，如圖2，因兩個圖象沒有交點，故f(x)沒有零點，不合題意.

3.當a>0時，兩個函數的圖象的交點個數可能有0、1、2三種情況，而依題只需1個交點，從而兩個函數圖象如圖3.

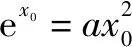
依題可得：曲線t(x)=ex與k(x)=ax2在x=x0處的切線是同一直線，故ex0=2ax0②.