“數(shù)形結(jié)合”思想在高中數(shù)學(xué)中的應(yīng)用
藺興旺
(甘肅省張掖市山丹第一中學(xué) 734100)
數(shù)學(xué)這門學(xué)科的學(xué)習(xí)在學(xué)生的學(xué)習(xí)生涯中的重要性不言而喻,并且數(shù)學(xué)不僅是學(xué)生學(xué)習(xí)的重要學(xué)科,也是促進(jìn)科學(xué)發(fā)展、促進(jìn)社會進(jìn)步的重要學(xué)科.而數(shù)學(xué)的主要研究方向就是數(shù)量關(guān)系和空間形式,說白了就是主要研究數(shù)、形的一門學(xué)科.因此,在高中數(shù)學(xué)中,靈活地運(yùn)用數(shù)形結(jié)合思想是學(xué)好數(shù)學(xué)所必要的.但是,由于高中學(xué)生受到思維方式和生活經(jīng)驗的限制,數(shù)形結(jié)合的思想還不能很好地靈活運(yùn)用.所以,高中數(shù)學(xué)教師就有必要重視數(shù)形結(jié)合思想解題方法的教學(xué)了.筆者總結(jié)了一些高中數(shù)學(xué)中運(yùn)用數(shù)形結(jié)合思想的解題方法,涵蓋了高中數(shù)學(xué)中大部分要運(yùn)用數(shù)形結(jié)合思想來解題的題型.
一、數(shù)形結(jié)合思想概論
數(shù)學(xué)的起源就是古人研究的數(shù)形關(guān)系,數(shù)和形是數(shù)學(xué)研究的基本對象,其在某些條件下可以互相的轉(zhuǎn)換.在高中數(shù)學(xué)中,也是研究數(shù)形的關(guān)系,而數(shù)形結(jié)合就是數(shù)與形的關(guān)聯(lián).數(shù)形結(jié)合是一種數(shù)學(xué)思想,其有兩種模式:一是使用數(shù)來闡述形的特點(diǎn)和屬性,二是使用形來直觀地表示數(shù)之間的關(guān)系.
筆者總結(jié)了在高中數(shù)學(xué)中運(yùn)用數(shù)學(xué)思想的解題方法主要在三個方面:1.運(yùn)用數(shù)形結(jié)合思想解決函數(shù)問題.2.運(yùn)用數(shù)形結(jié)合方法解決不等式問題.3.運(yùn)用數(shù)形結(jié)合解決平面幾何問題.前兩種都是用形來直觀表示數(shù)之間關(guān)系的數(shù)形結(jié)合思想,第三種是使用數(shù)來闡述形的屬性特點(diǎn).
這些題型包含了高中數(shù)學(xué)中的大量題型,相信如果掌握了這些數(shù)形結(jié)合的思想方法并且靈活的運(yùn)用,就能夠提高數(shù)學(xué)的成績.所以,教師要在日常教學(xué)中貫穿這些數(shù)形結(jié)合思想方法的教學(xué),因為這些數(shù)形結(jié)合思想對學(xué)生的數(shù)學(xué)學(xué)習(xí)很有幫助.下面,筆者就結(jié)合一些例題來演示這些數(shù)形結(jié)合思想的解題方法.
二、數(shù)形結(jié)合思想解決函數(shù)問題
數(shù)形結(jié)合思想在函數(shù)問題中的運(yùn)用很廣泛,比如在函數(shù)的最值、值域、取值范圍問題上,函數(shù)的單調(diào)性、奇偶性上,甚至在函數(shù)的概念性問題上都有運(yùn)用.
例題1(函數(shù)的概念問題)下列選項中,哪個選項的函數(shù)存在反函數(shù).
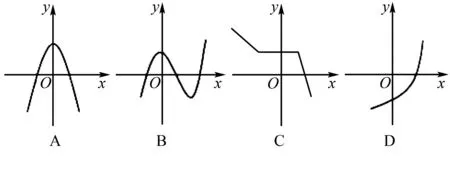
這個問題可以由反函數(shù)的定義得出答案:
由此可以得到有反函數(shù)的函數(shù)在“形”上的特點(diǎn)是x與y只能一一對應(yīng),所以此題應(yīng)當(dāng)選D選項.
例題2(函數(shù)取值范圍問題)設(shè)函數(shù)y=x2+2ax+1在(+∞,1]上為減函數(shù),求a的取值范圍.
對于此類問題應(yīng)當(dāng)運(yùn)用數(shù)形結(jié)合思想來解答:
由函數(shù)解析式可得函數(shù)圖象的對稱軸為x=-a.
∵此函數(shù)在(+∞,1]上單調(diào)遞減.
∴由函數(shù)圖象特征可得對稱軸x=-a必須在直線x=1上或者在直線x=1的右側(cè),有-a≥1.
∴得到a≤-1.
例題3(函數(shù)單調(diào)性、奇偶性問題)設(shè)奇函數(shù)f(x)在[3,7]上單調(diào)遞增,并且函數(shù)在此區(qū)間上的最小值為6,求此函數(shù)在區(qū)間[-7,-3]上的單調(diào)性以及最大值.
這個問題可以通過函數(shù)特征結(jié)合圖象來解答:
∵f(x)為奇函數(shù),
∴f(x)的圖象關(guān)于原點(diǎn)O對稱.
∵f(x)在[3,7]上單調(diào)遞增,在此區(qū)間上最小值為6,
∴f(x)在[-7,-3]單調(diào)遞增,并且最大值為-6.
三、數(shù)形結(jié)合思想解決不等式問題
在不等式問題中運(yùn)用數(shù)形結(jié)合思想來解答,可以避免復(fù)雜的分類討論,簡化題目,直接利用幾何圖形特點(diǎn)得出答案.
例題4 設(shè)有關(guān)于x的不等式|x-3|+|x-4| 解設(shè)函數(shù)f(x)=|x-3|+|x-4|,函數(shù)g(x)=a,在平面直角坐標(biāo)系中作出函數(shù)f(x)和g(x)的圖象如下. 由函數(shù)f(x)和g(x)的圖象特征可得要使|x-3|+|x-4| 所以可得a的取值范圍為(-∞,1]. 例題5設(shè)函數(shù)f(x)=x2-2ax+2, 并且x∈[-1,+∞)時,f(x)≥a恒成立,求a的取值范圍. 對于此題有兩種解法: 解法1由當(dāng)x∈[-1,+∞)時,f(x)≥a恒成立可得x2-2ax+2-a≥0在x∈[-1,+∞)時恒成立. 所以題目可以化為求a的取值范圍使得函數(shù)g(x)=x2-2ax+2-a的圖象在區(qū)間[-1,+∞)位于x軸上方.作出圖象,有如下兩種情況: 由圖象可得不等式的成立條件是: (1)Δ=4a2-4(2-a)<0?a∈(-2,1). 綜上所述a的取值范圍是(-3,1). 解法2由f(x)≥a可得x2-2ax+2≥a即x2+2>a(2x+1). 設(shè)函數(shù)f(x)=x2+2,函數(shù)g(x)=a(2x+1),作出函數(shù)f(x)和函數(shù)g(x)的圖象. 由函數(shù)圖象特征可得a的取值范圍為圖中直線斜率的取值范圍. 即a的取值范圍是(-3,1). 在高中數(shù)學(xué)中,平面解析幾何知識是運(yùn)用到數(shù)形結(jié)合思想最廣泛的知識點(diǎn),在直線斜率、直線與圓、直線與圓錐曲線等問題上,運(yùn)用數(shù)形結(jié)合思想解題是最為簡捷的. 例題6 (直線斜率問題)直線l過點(diǎn)P(-1,2),且與點(diǎn)A(-2,-3)、B(4,0)為端點(diǎn)的線段AB相交,求直線l的斜率的取值范圍. 在解這類題目時,先作出直線PA、PB,線段AB. 例題7 (直線與圓問題)設(shè)圓O的方程為x2+y2-2x+4y+4=0,直線l的方程為3x-4y+9=0,求圓O上的點(diǎn)P到直線l上的最大距離為多少. 在解這類問題時,運(yùn)用數(shù)形結(jié)合思想能使問題得到迅速解決. 將圓的方程配方可得(x-1)2+(y+2)2=1,由此可得圓心O為(1,-2),半徑r=1. 由直線與圓的圖形特征可得:圓到直線的最大距離=圓心到直線的距離+半徑. 圓心O到直線l的距離d=4.由上式可得點(diǎn)P到直線l的最大距離為d+r=4+1=5. 例題8(直線與圓錐曲線問題)設(shè)點(diǎn)P是拋物線y2=2x上的動點(diǎn),F(xiàn)是此拋物線的焦點(diǎn),設(shè)點(diǎn)A(3,2),求|PA|+|PF|的最小值. 對于這個問題,先畫出拋物線和準(zhǔn)線. 由拋物線的定義可得PF=PM,所以|PA|+|PF|=|PA|+|PM|. 總而言之,數(shù)形結(jié)合思想在高中數(shù)學(xué)的學(xué)習(xí)中對學(xué)生是非常有幫助的,其在高中數(shù)學(xué)中的運(yùn)用非常廣泛,比如在函數(shù)問題、不等式問題、平面解析幾何中都有非常廣泛的運(yùn)用.運(yùn)用數(shù)形結(jié)合思想來解這些題目可以非常簡捷迅速地得出答案.學(xué)生如果掌握和運(yùn)用好了數(shù)形結(jié)合思想,就能更加輕松地學(xué)習(xí)數(shù)學(xué),提高考試成績.所以,高中數(shù)學(xué)教師在日常的教學(xué)中要始終貫穿數(shù)形結(jié)合思想的教學(xué),讓學(xué)生掌握好這一數(shù)學(xué)思想并且靈活地運(yùn)用.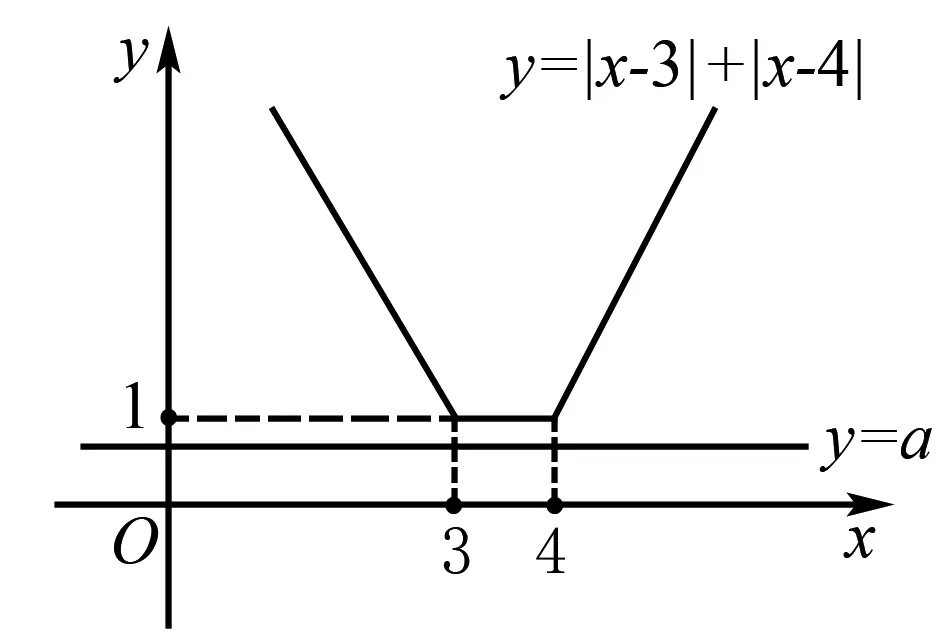


四、數(shù)形結(jié)合思想解決平面解析幾何問題