基于多智能體的電動汽車滑移率控制方法
張裊娜,張曉芳
(長春工業大學 電氣與電子工程學院,吉林 長春 130012)
0 引言
在電動汽車安全行駛過程中,制動穩定性是非常重要的一部分,而滑移率的控制直接影響電動汽車的制動穩定性。電動汽車制動滑移率控制為通過主動調節車輪力矩,確保車輪滑移率能維持在最優滑移率附近,使車輪獲得較高的縱向附著力,防止車輪抱死現象的發生,從而提高汽車制動安全性。與傳統汽車制動系統相比,電動汽車的執行部件是輪轂電機,其響應速度更快、執行效率更高,更加適合現代控制策略的應用[1]。滑移率控制的難點主要在于如何解決制動系統中的非線性和強不確定性問題[2]。Castro R D和Rui E A等[3]將一種防飽和條件積分滑模算法應用到滑移率的控制中,它根據期望轉矩來估計附著系數的不確定性上界,從而提高了系統的魯棒性和穩態精度,抑制了滑模控制系統中的抖振現象。但缺點是算法中使用的積分效應使系統中的動態性能降低。戴彥[4]提出了將模糊規則與滑模控制相結合的控制算法,對滑模控制中的切換項進行模糊化,使切換控制項在保證魯棒性的前提下盡可能小,從而解決了制動系統滑模控制中的抖振問題。Castro R和Araujo R E等[5]提出將蓄電池SOC和機電復合響應帶寬的影響考慮到滑移率的控制中,提出了一種魯棒自適應控制算法,使得系統中的控制量由自適應項產出,提高了系統的響應速度。Yuan L和Zhao H等[6]將一種預測控制算法應用到電動汽車滑移率控制系統中,通過同時控制4個車輪的力矩,使4個車輪的滑移率維持在最佳滑移率附近,保證汽車在安全行駛的前提下,能夠獲得較大的驅動制動力,同時防止了電動汽車驅動時過度滑移與制動時車輪抱死情況的發生。
目前,計算機技術的蓬勃發展極大提高了復雜動態系統的發展速度。將智能體之間的協調配合應用到復雜的工作中,可大大提高工作效率與系統靈活性和魯棒性[7]。因此,基于復雜系統的多智能體協調控制擁有著廣闊的發展空間,目前國內外許多學者對多智能體系統進行長期和深入的研究。多智能體及其相關技術已經廣泛應用于多電機控制、智能機器人、新能源電動汽車、分布式控制、計算機控制、交通控制、電子商務等多領域中[8-10]。伴隨著電動汽車和多智能體的迅速發展,將多智能體技術應用到電動汽車的協調與控制中成為一個熱點方向。
本文首先對電動汽車制動工況進行動力學分析,建立一個車輪的滑移率模型,然后將每個車輪及其控制器看成智能體,將多智能體理論應用于4個車輪的同步協調控制研究中,然后分別采用普通滑模和非奇異終端滑模對滑移率進行控制,并利用Lyapunov理論進行穩定性分析。最后,通過仿真軟件MATLAB中的Simulink進行實驗驗證,驗證了算法的有效性。
1 系統動力學分析
1.1 車輛制動系統模型
在電動汽車制動過程中,當不考慮輪胎與地面的滾動阻力和空氣阻力,其受力情況如圖1所示,可將運動方程表達為如下[11]:
車輛運動方程:
(1)
車輪運動方程:
(2)
車輪縱向摩擦力:
Fx=Nμ=μmg,
(3)
式中:m為1/4車體重量,v為車輛行進速度,Fx為車輪縱向摩擦力,N為車輪對地面的法向反力,μ為車輪與地面的附著系數,I為車輪轉動慣量,ω為車輪角速度,R為車輪半徑,Tb為制動力矩。
圖1 車輛制動時動力學模型
Fig.1 Vehicle dynamic model under braking
電動汽車制動時會導致車速與車輪轉速產生偏差,進而車輪與地面之間會產生滑移問題,滑移程度的大小用滑移率來表示[12]:
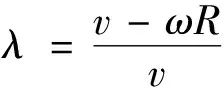
(4)
分別對λ求其一階,二階導數得
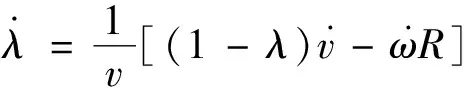
(5)
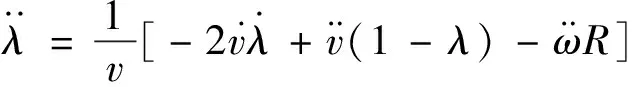
(6)
將式(2)、(3)代入式(5)、(6)中得
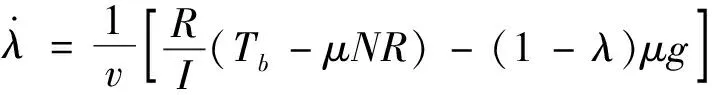
(7)
(8)
由式(1)和式(3)可得
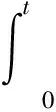
(9)
其中,v0為車輛制動時的初始速度。將式(9)代入式(8)中,并令
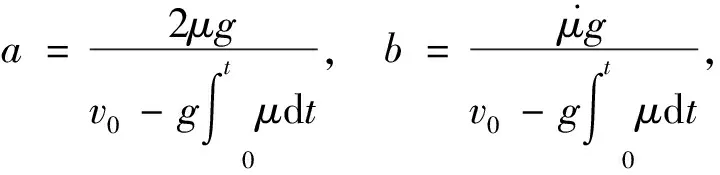
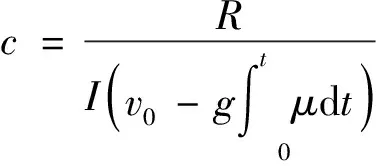
則式(8)可以寫為
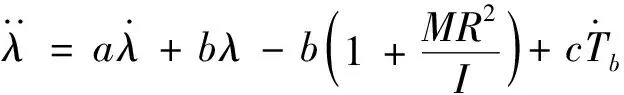
(10)
1.2 車輪輪胎模型
在不同的輪胎和路面附著條件下,輪胎的附著系數和滑移率之間的非線性關系曲線是不同的,輪胎的最大附著系數所對應的最優滑移率大小也不相同。在對最優滑移率的跟蹤中,可采用通過已知輪胎模型的實驗參數,經過推導計算來獲得不同典型路面條件下的最優滑移率。
為了便于分析研究,本文采用的是結構簡單實用的Burckhardt輪胎模型,通過模型參數來求取不同路面下的最優滑移率。Burckhardt輪胎模型具體表達式為[13]
μx=c1[1-e-c2λ]-c3λ,
(11)
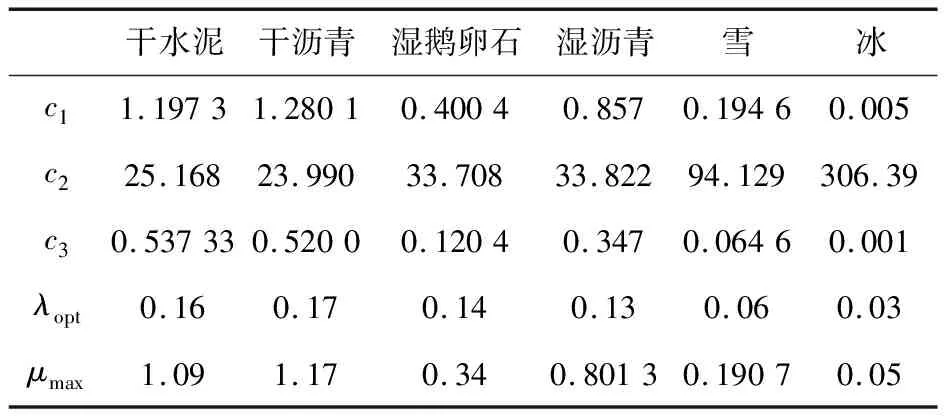
其中c1,c2,c3為擬合系數,取值大小和具體的輪胎與路面附著條件有關。
由式(11)可分別求得路面最優滑移率和路面峰值附著系數為
本文選取6種常用標準路面作為對比道路,具體參數如表1。
表1 不同路面的最優滑移率及其附著系數
Tab.1 Optimal slip ratio of different pavements and its adhesion coefficient
干水泥干瀝青濕鵝卵石濕瀝青雪冰c11.19731.28010.40040.8570.19460.005c225.16823.99033.70833.82294.129306.39c30.537330.52000.12040.3470.06460.001λopt0.160.170.140.130.060.03μmax1.091.170.340.80130.19070.05
2 控制算法研究
2.1 基于普通滑模的多智能體滑移率控制
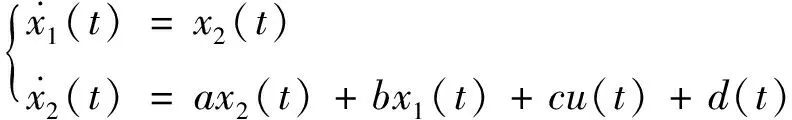
定義e1(t)=x1d-x1(t),e2(t)=x2d-x2(t)。
選取滑模變結構系統的滑模面為
s(t)=εe1+e2(t),
(12)
采用等速趨近率:
(13)
從而得出單個車輪的滑移率控制率為
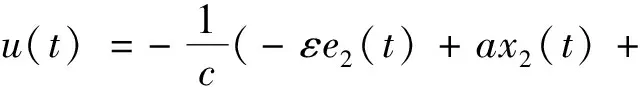
bx1(t)-ksgn(s(t)))。
(14)
由四輪輪轂電機電動汽車連接結構和內部工作原理可得多智能體系統的拓撲結構,如圖2所示。設計智能體0為虛擬領導者智能體,4個車輪分別為智能體1,2,3,4。虛擬領導者智能體通過Burckhardt輪胎模型獲得典型路面的最優滑移率,4個跟隨者智能體跟蹤領導者智能體的狀態。
由多智能體的定義性質可得,系統相應的鄰接矩陣A、入度矩陣D和拉普拉斯矩陣L分別為
圖2 多智能體系統拓撲結構圖
Fig.2 Multi agent system topology diagram
智能體i與領導者之間的連接權值用bi來表示,在這里假設,如果智能體i和領導者連通,則bi=1;否則,bi=0。由圖2得B=diag(1,1,1,1)。
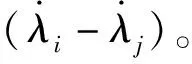
(15)
上式即為多智能體一致性控制協議,下面證明在該控制率下系統的穩定性。4個車輪分別跟蹤虛擬領導者智能體運動,取:
,
(16)
將(15)和(16)代入(10)得4個車輪系統的表達式:
(17)
取矩陣M=L+B,則(17)可以表示為
(18)
K=diag(k1,k2,k3,k4),ε=diag(ε1,ε2,ε3,ε4),
證明系統穩定性,選取Lyapunov函數:
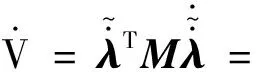
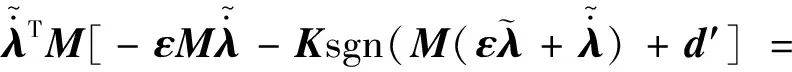
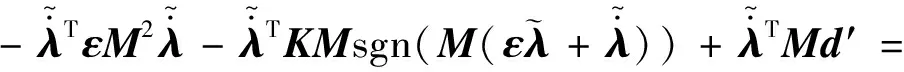
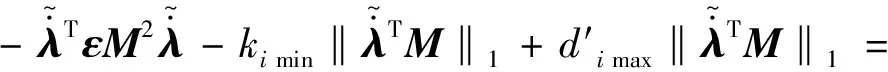
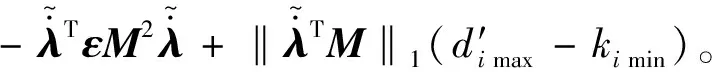
2.2 基于非奇異終端滑模的多智能體滑移率控制
考慮到普通滑模的有限時間收斂性和終端滑模的奇異性問題,本小節采用改進后的非奇異終端滑模控制算法進行制動滑移率控制。
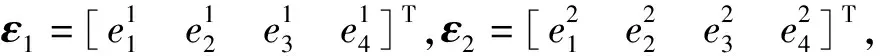
(19)
i=1,2,3,4。
令控制率U=[u1u2u3u4]T,則誤差動態方程可以表示為
(20)
其中,d代表不確定性及外部干擾,di≤lg。
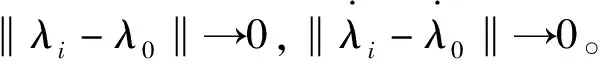
(21)
其中,α=q/p,且奇數p,q滿足1 (22) 可設計如下的控制率[14]: (23) 其中,η>0。 則滑模變量S能夠在有限時間內到達滑模面S=0,達到系統的穩定。 其中: 即: 將(23)代入(20)得 由相軌跡特性可知,當ε2=0時,在有限時間內能夠實現S=0。 在基于MATLAB的Simulink中搭建系統仿真模型,進行實驗仿真。仿真參數:車輪滾動半徑R=0.3 m,單輪車輛垂直載荷m=290 kg,(注意:前兩個車輪的垂直載荷要大于后兩個車輪垂直載荷),車輛轉動慣量I=0.8 kg·m2,制動時車輪初始速度25 m/s。分別選取基于固定滑移率和干水泥路面兩種工況條件下進行制動仿真實驗。 車輛在基于固定滑移率工況下,車輪最優滑移率λd=0.2,對應路面最大附著系數μf=0.88;在此路面下的仿真結果如下: 采用普通滑模的多智能體算法和非奇異終端滑模的多智能體算法下的四個車輪滑移率仿真圖如圖3和圖4所示。制動過程以左前輪為例,輪速和車速的仿真圖如圖5所示,兩種算法下的制動距離如圖6所示。 圖3 普通滑模多智能體控制算法下的4個車輪滑移率 Fig.3 Slip rate of four wheels based on common sliding mode multi-agent control algorithms 圖4 非奇異終端滑模多智能體控制算法下的4個車輪滑移率 Fig.4 Slip rate of four wheels based on nonsingular terminal sliding mode multi-agent control algorithms 圖5 兩種滑模多智能體控制算法下左前車輪的車身速度與車輪速度關系曲線 Fig.5 Relationship curve between body speed and wheel speed of left front wheel based on two sliding mode multi-agent control algorithms 圖6 兩種滑模多智能體控制算法下的車輛制動距離 Fig.6 Vehicle braking distance based on two sliding mode multi-agent control algorithms 由仿真分析圖可知,兩種基于多智能體的滑模算法都很好地滿足了汽車的制動安全性。首先分析基于普通滑模的多智能體控制算法,由圖3可得,電動汽車四個車輪的滑移率在t=0.5 s時都快速到達最佳滑移率附近,滿足了電動汽車制動性能的要求,但4個車輪最后在約t=2.7 s時達到最優滑移率λd=0.2。以左前輪為例,由圖5和圖6可得電動汽車在約t=3.17 s,車速和輪速趨于零,汽車制動結束,制動距離約為39.7 m。分析基于非奇異終端滑模的多智能體控制算法,由圖4可得,約在t=1.5 s時四個車輪的滑移率迅速一致地達到了最佳滑移率λd=0.2。同樣以左前輪為例,由圖5和圖6可得,約在t=3 s車速和輪速趨于零,汽車制動結束,制動距離約為38.8 m。 選取車輛運行在干水泥路面情況下進行仿真實驗,干水泥路面的最優滑移率為λd=0.16,路面最大附著系數為μf=1.09,在此路面下進行仿真實驗的結果分析如下。 采用普通滑模的多智能體算法和非奇異終端滑模的多智能體算法下的四個車輪滑移率仿真圖如圖7和圖8所示。制動過程以左前輪為例,輪速和車速的仿真圖如圖9所示,兩種算法下的制動距離如圖10所示。 圖7 普通滑模多智能體控制算法下的4個車輪滑移率 Fig.7 Slip rate of four wheels based on common sliding mode multi-agent control algorithms 圖8 非奇異終端滑模多智能體控制算法下的4個車輪滑移率 Fig.8 Slip rate of four wheels based on nonsingular terminal sliding mode multi-agent control algorithms 首先分析基于普通滑模多智能體滑移率控制算法,由圖7可得,電動汽車四個車輪的滑移率在t=0.6 s時都快速到達最優滑移率附近,滿足了電動汽車制動性能的要求。但4個車輪最后到約t=2 s時達到了最優滑移率λd=0.16。同樣以左前輪為例,由圖9和圖10可得,電動汽車在大約t=2.445 s時車速和輪速都趨于0,汽車制動結束,制動距離約為31 m。分析在基于終端滑模的多智能體控制算法下,由圖8可得,約在t=1.2 s時四個車輪滑移率都已達到了最優滑移率。以左前輪為例,由圖9和圖10可得,在約t=2.1 s時,電動汽車的車速和輪速都趨于0,汽車制動結束,制動距離約為28.5 m。 圖9 兩種滑模多智能體控制算法下左前車輪的車身速度與車輪速度關系曲線 Fig.9 Relationship curve between body speed and wheel speed of left front wheel based on two sliding mode multi-agent control algorithms 圖10 兩種滑模多智能體控制算法下的車輛制動距離 Fig.10 Vehicle braking distance based on two sliding mode multi-agent control algorithms 針對電動汽車制動過程中滑移率的控制是非線性、不確定性的時變系統,將多智能體理論和滑模控制算法相結合,并分別設計了基于普通滑模多智能體的控制策略和基于非奇異終端滑模多智能體的控制策略對電動汽車制動滑移率進行控制,最后選擇車輛在標準均勻路面與干水泥路面兩種路面工況下進行實驗仿真。證明了本文提出的兩種控制策略均能滿足車輛制動穩定性的需求,其中基于非奇異終端滑模的多智能體控制策略效果更好些,使車輛的制動時間和制動距離更短。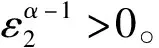
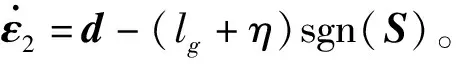
3 仿真研究
3.1 基于固定滑移率的多智能體算法控制仿真
3.2 基于干水泥路面的多智能體算法控制仿真
4 結論

