基于非對稱極值Copula的設計暴雨過程線分析
陳子燊,趙玲玲,楊興
(1. 中山大學新華學院,廣東廣州510520;2.中山大學地理科學與規劃學院, 廣東廣州510275; 3. 廣州地理研究所,廣東廣州510070;4.安徽理工大學地球與環境學院,安徽淮南232000)
臺風災害是全球發生頻率最高的一種自然災害。臺風帶來的極端降雨過程可導致山洪暴發和衍生滑坡等地質災害,從而造成重大的生命財產和經濟損失。如何應對極端暴雨是城市和山地防災減災都需面對的重大問題。一些研究人員從城市應對極端天氣事件與防災減災的風險管理角度對雨型作了探索。蔣明[1]指出,雨型是描述降雨過程和降雨強度在時間尺度上的分配過程, 是徑流過程計算的基礎。成丹等[2]把設計雨型作為制定排水防澇系統設計時的重要因素,應用于城市市政排水系統的規劃和管理及排水分析,為城市流域雨洪調度計算提供科學依據。葉姍姍等[3]選取宿遷市實測的主副型雨峰偏后的暴雨雨型,對其降雨過程進行同頻率分時段縮放,采用Copula 函數的風險聯合概率模型分析了不同的兩時段之間出現的暴雨風險。楊星等[4]利用深圳雨量站34 a實測逐時降雨資料,對比了不同典型暴雨設計雨型研究方面的差異,按構建的兩變量Copula推求了深圳市不同重現期雨型的風險率和典型暴雨的特征。
山區中小流域山洪至今仍然是防災減災的重要研究方向,為此,可借鑒設計洪水過程線的方法,從高維(大于二維)尺度上設計典型暴雨過程,將更有利于山洪風險管理。至今在應用Copula函數分析三變量洪水的聯合概率分布和設計洪水過程線已有不少研究。侯蕓蕓等[5]和ZHANG等[6]分別應用對稱的單參數Archimedean Copula函數分析了洪水三變量的聯合概率分布和條件概率分布。由于具有不同相關性的高維隨機變量,單參數難以真實反映其復雜的不對稱相關結構。非對稱形式的Copula 函數具有更加靈活的參數和結構形式,更適合用于擬合高維的隨機變量[7 ]。為此,Grimaldi等[8]、Ganguli等[9]、陳子燊等[7]分別采用非對稱的阿基米德Copulas(Asymmetric Archimedean Copulas)構建了不對稱三變量洪水要素聯合分布模型推算設計洪水,以嘗試應用于洪水風險規劃管理。肖義等[10]和李天元等[11]則分別采用兩變量和三變量的Copula函數建立了聯合分布的設計洪水過程線的推求方法,為設計洪水過程線提供了一種新思路。本文把非對稱阿基米德極值Copula用于構建山區中小流域設計暴雨過程線,希望有助于防災減災的風險管理。
1 三變量Copula函數
1.1 Copula函數的定義
設隨機變量Xi(i=1,2,…,n)的邊緣分布函數分別為FXi(xi)=P(Xi≤xi),其中n為隨機變量的個數,xi為隨機變量Xi的值。依Sklar理論,對于連續分布函數FXi(xi),存在唯一的聯合分布函數[6]:
H(x1,x2,…,xn)=C(FX1(x1),FX2(x2),…,FXn(xn))=C(u1,u2,…,un)
(1)
利用Copula函數構造聯合概率分布,使得變量的所有信息都存在于邊緣分布函數里,不會在轉換過程中產生信息失真。因此,Copula函數理論是構建多變量水文聯合概率分布的很好的工具[12]。
1.2 三變量Archimedean Copula
三變量對稱的Archimedean Copula單參數形式[13]為:
(2)
式中uj∈[0,1](j>1)——邊緣分布;φθ——Archimedean Copula生成元,θ——參數。
φθ(u3)]
(3)

三變量非對稱Archimedean Copula的形式為[14]:
C(u1,u2,u3)=C1(u3,C2(u1,u2))=
(4)
式中 符號“0”——函數組合。
常用的三維非對稱Archimedean族Copula函數如下。
a) M3 (Frank) Copula
(1-e-θ1u3))},θ2>θ1∈[0,∞)
(5)
b) M4 (Clayton) Copula
(6)
c) M5 (Arch2) Copula
(7)
d) M6(Gumbel-Hougaard) Copula
C(u1,u2,u3)=exp{-([(-lnu1)θ2+(-lnu2)θ2]θ1/θ2+(-lnu3)θ1)1/θ1},θ2>θ1∈[1,∞)
(8)
e) M12 (Arch12) Copula
(9)
1.3 三變量聯合重現期和條件重現期
以算符“∨”定義“或”三維極端事件中至少有一個被超過情況下的“或”聯合重現期為:
(10)
以“∧”定義“且”三維極端事件同時被超過情況下的“且”聯合重現期為:
(11)
2個不超過事件發生下的條件概率為[5]:
(12)
則事件(X1>x1|X2≤x2,X3≤x3)下的條件重現期為:
T(x1|X2≤x2,X3≤x3)=
(13)
2個等量事件發生下的條件概率為:
F(x1|X2=x2,X3=x3)=
(14)
則事件(X1>x1|X2=x2,X3=x3)下的條件重現期為:
T(x1|X2=x2,X3=x3)=
(15)
一個等量事件發生下的條件概率為:
(16)
則事件至少有一個為超過事件下的條件重現期為:
(17)
一個不超過事件發生下的條件概率為:
(18)
則事件至少有一個為超過事件下的條件重現期為:
(19)
2 實例研究
2.1 流域水文氣象背景與基本數據
選取廣東曹江流域為實例研究。曹江是廣東獨流入海鑒江的一級支流,發源于高州馬貴鎮山心村的藍蓬嶺。出口斷面大拜水文站集水面積394 km2,屬于典型的中小流域。曹江流域多年平均年雨量約2 160 mm,最大年雨量可達3 150 mm,是廣東的臺風暴雨高區之一。1967年11月7日代號為6720 的“Emma”超強臺風,在流域西側的湛江市登陸,最大風速65 m/s,中心氣壓912 hPa。2013年8月14日代號為“Utor”的超強臺風,在流域東側的陽江市登陸,最大風速60 m/s,中心氣壓925 hPa。大拜雨量站測得二者最大24 h暴雨分別為419.9、412.1 mm,均達到特大暴雨級別,也是1967—2013年2個最大的24 h小時雨量。
本文根據曹江流域出口斷面大拜雨量站1967—2013年逐時降水記錄數據,首先提取歷年最大24 h雨量(R24),再分別提取最大1 h雨量(雨峰:R1)和連續最大6 h雨量(R6)數據,由R1、R6和R24作為實例分析的樣本,分別構建1967、2013年這3個歷時雨量聯合分布的2場設計暴雨過程線。
2.2 邊緣分布與聯合分布
分別采用皮爾遜三型分布(PE3)和廣義極值分布(GEV)對R1、R6和R24樣本加以擬合。參數估計使用線性矩(L-矩)方法。經驗頻率分布使用Gringorten公式計算。擬合結果采用均方根誤差(RMSE)和概率點據相關系數(PPCC)檢驗其擬合優度。表1擇優對比結果表明,R1、R6和R24都以GEV分布相對更優。廣義極值(GEV)分布函數為:
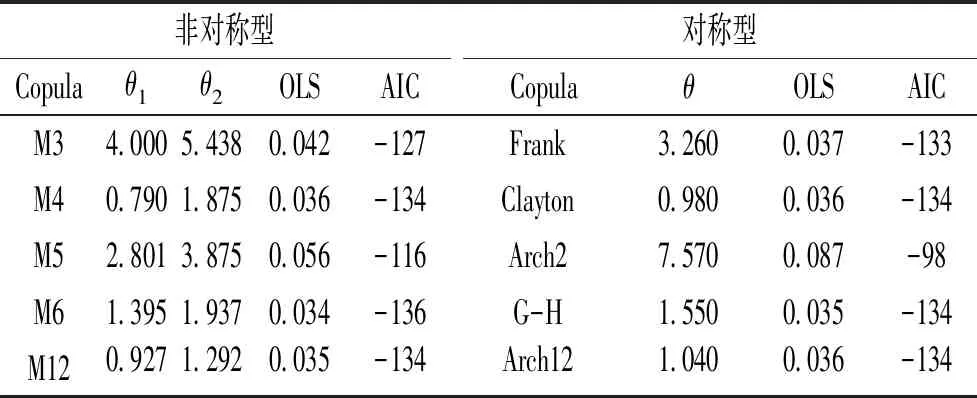
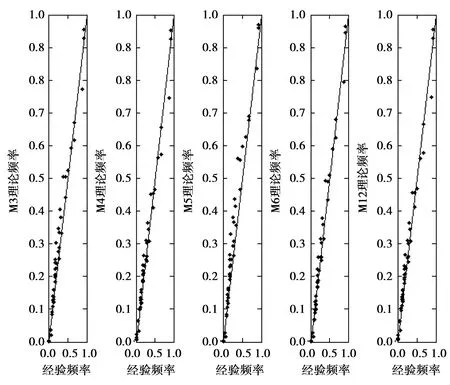
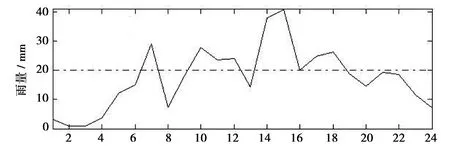
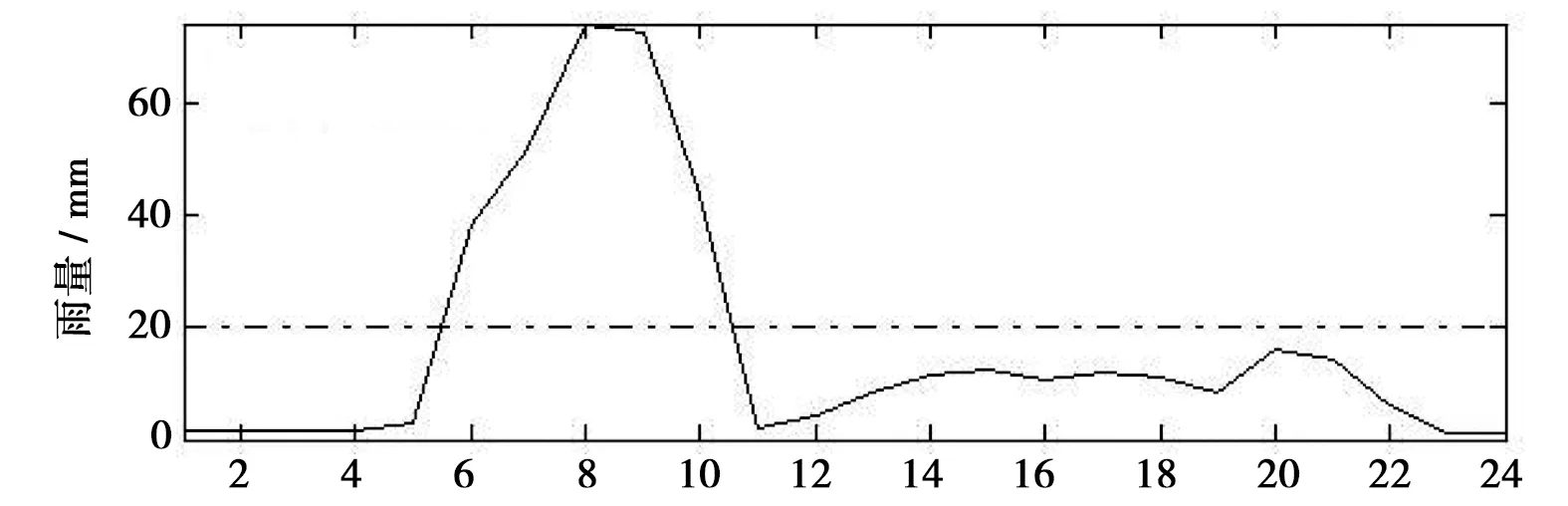
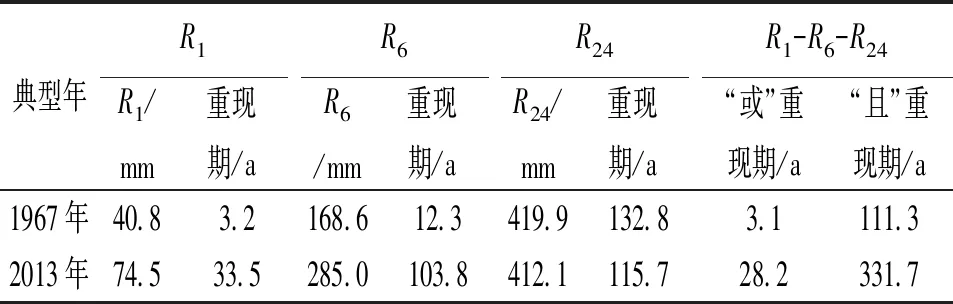
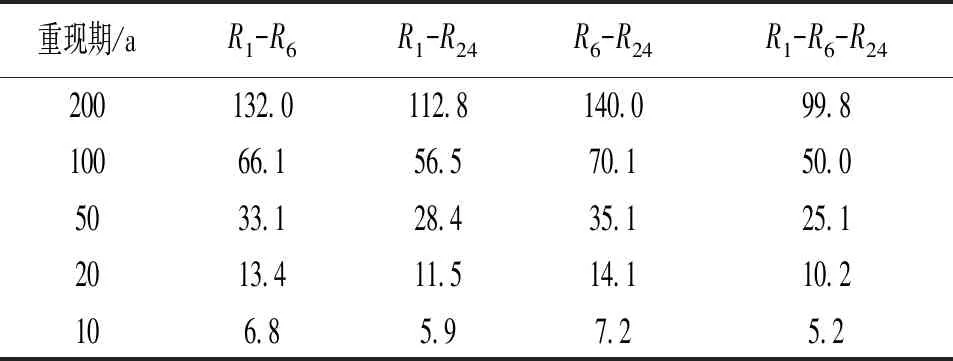
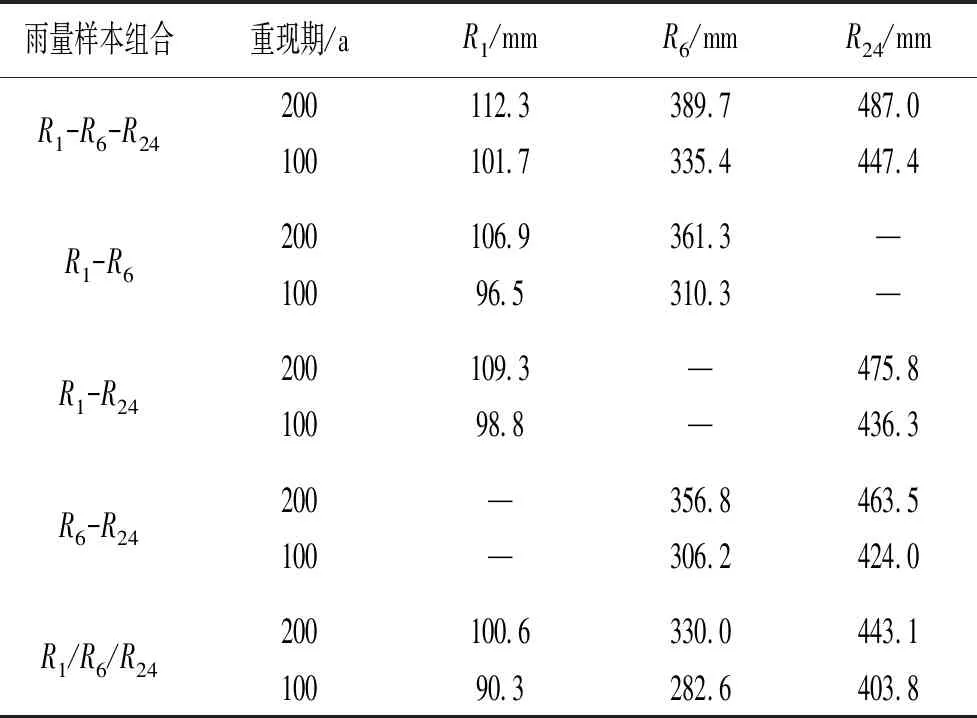
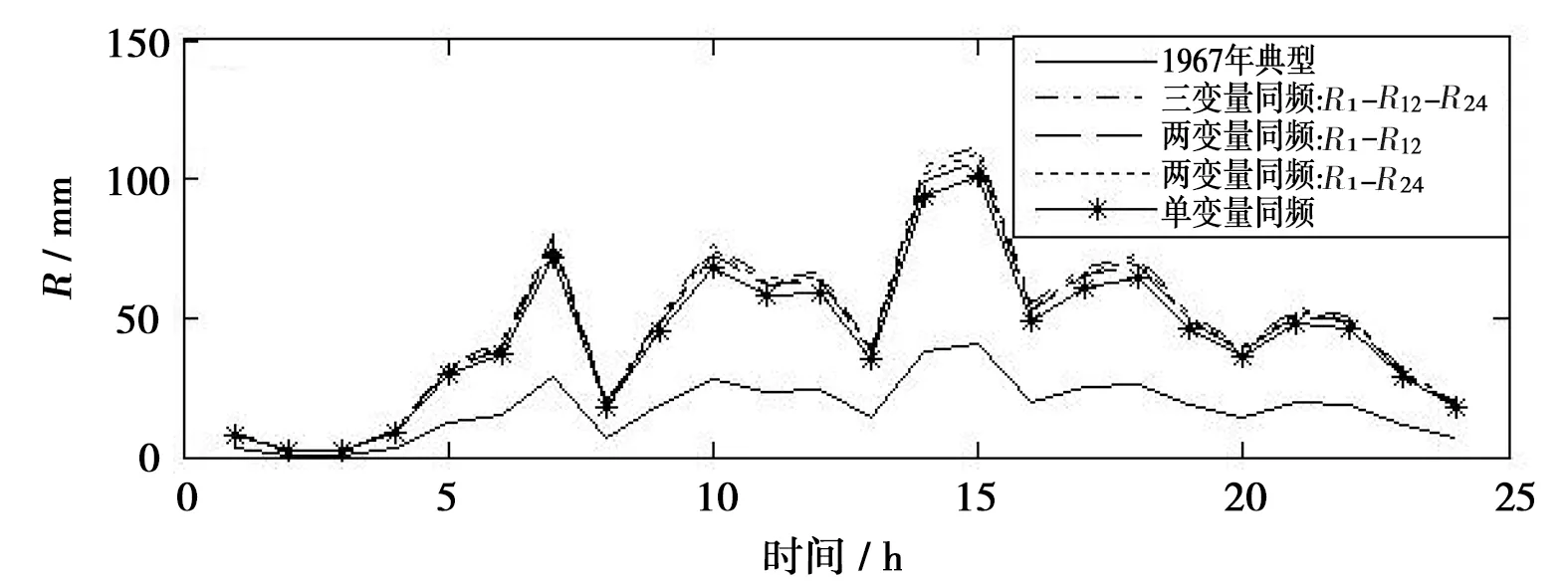
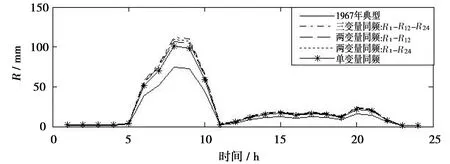
FX(x)=P(X (20) 式中ξ、β、μ——形態參數、尺度參數和位置參數。 表1 曹江大拜站三變量暴雨樣本的 邊緣分布參數與優度檢驗值 計算的R1、R6和R24兩兩間的Kendall 相關系數表明大拜雨量站不同歷時暴雨間都存在正相關性,其中R6和R24最強,τ= 0. 484;R1和R6相關性次之,τ=0.399;R1和R24相關性較弱,τ= 0.171。采用Kendall相關系數τ與Copula參數θ的關系式,構建5種非對稱Archimedean Copula[6]。為了對比,分別將對應的5種對稱三變量Archimedean Copula通過MLM法計算其參數θ。采用Akaike 信息準則(AIC)、最小(OLS)準則和Genest-Rivest圖形法驗證理論聯合分布函數與經驗聯合分布函數的擬合程度,結果見表2和圖1。可見以二維Gumbel-Hougaard 為基Copula的三維非對稱形式的M6 Copula 的OLS和AIC值最小,擬合度最高,各點均勻地分布在45°線左右的非對稱Archimedean M6 Copula具有相對最優的擬合度。Nelson[13]和Salvadori等[14]證明當且僅當邊緣分布和Copula函數均為極值分布時,構造的聯合分布才是極值分布,而Gumbel-Hougaard Copula是Archimedean Copula函數族中的唯一多變量極值Copula函數,適用于極端事件的頻率分析。考慮到R1、R6和R24之間的相關性存在明顯差別,因此,選用非對稱Archimedean M6 Copula構建大拜雨量站歷年最大24 h暴雨量不同歷時R1、R6和R24之間的三維聯合分布: C(u1,u2,u3)=exp{-([(-lnu1)1.937+ (-lnu2)1.937]1.395/1.937+(-lnu3)1.395)1/1.395} (21) 表2 非對稱和對稱三維Copula 參數估計及擬合優度對比評價 a) M2 b) M4 c) M5 d) M6 e)M12圖1 5種非對稱Archimedean Copula的概率分布擬合 典型暴雨的特征,包括降雨集中程度、雨峰位置和雨峰大小等。典型暴雨過程線的選擇采用以下原則: ①選擇雨峰量大具有一定代表性的實測暴雨過程線;②從防洪安全考慮,對主峰靠后和主峰靠前的2種雨型的風險概率加以對比;③設計暴雨過程線采用同頻率放大法,以降水主峰對流域洪水形成為首要影響因子,選定時段為1 h的設計雨峰為設計標準,使得放大的過程線形狀能與原來的典型過程一致。 按照短歷時強降水強度20 mm/h劃分雨峰,根據典型年暴雨過程的雨峰位置,選取1967、2013年作為曹江流域設計暴雨的典型年,24 h暴雨過程線見圖2。圖2顯示,1967年最大24 h暴雨過程為主副多峰雨型,主峰靠后,2013年最大24 h暴雨過程為單峰雨型,主峰靠前。這2個典型暴雨R1、R6、R243個時段最大降水量與相應的重現期見表3。 a) 1967年 b) 2013年圖2 2個典型年的最大24 h暴雨過程 > 表3 2個典型年R1、R6、R24最大降水量及重現期 典型年R1R1/mm重現期/aR6R6/mm重現期/aR24R24/mm重現期/aR1-R6-R24“或”重現期/a“且”重現期/a1967年40.83.2168.612.3419.9132.83.1111.32013年74.533.5285.0103.8412.1115.728.2331.7 從表3可見,1967、2013年的R1-R6-R24組合雨量的“或”聯合重現期小于單一時段雨量重現期,此說明考慮多時段組合條件下某一時段雨量致災的可能性最高,相比較同時出現三時段組合雨量的“且”聯合重現期可能性很小。表4為不同時段雨量組合的“或”聯合重現期,可見同頻率下R1-R6-R24三時段組合雨量的“或”聯合重現期最小,危險率最高。因此,如果以三時段雨量組合的“或”聯合重現期作為流域的防雨洪標準,由此設計的暴雨過程線對于應對流域雨洪風險更合適。 表4 不同時段雨量組合的“或”聯合重現期 有關研究指出[11],由于對任一給定的三變量重現期Tu1,u2,u3,理論上存在無數種u1、u2、u3的組合滿足式(10),如果按照同頻率放大法的思路,假定R1、R6、R243個時段雨量同頻率,即令u1=u2=u3,可得到基于某一聯合重現期Tu1,u2,u3的頻率組合(u1,u2,u3)。根據此組合,按照各變量的邊緣分布函數反推可得到3個不同時段雨量的聯合設計值組合(r1、r6、r24),進而以此設計值組合放大典型暴雨過程,即得到基于三變量聯合分布的設計暴雨過程線。采用非對稱M6函數推算R1、R6、R243個時段雨量同頻率分布聯合設計值公式如下: u1=u2=u3=[1-(1/Tu1,u2,u3)]α; (22) 按相同原理,可分別推算兩變量u1、u2的重現期Tu1、u2,u1、u3的重現期Tu1、u3和u2、u3的重現期Tu2,u3的同頻率分布聯合設計值。 從表5多變量同頻率設計值計算結果可見,R1-R6-R24組合同頻率設計暴雨設計值明顯大于其它同一重現水平組合和單一時段暴雨的設計值。由于多變量方法是基于多個時段組合的聯合重現期,考慮了變量之間的相關性,設計值會大于單變量同頻率設計值。有關研究結果顯示[7,15],三變量同頻率設計值十分接近于按聯合概率密度最大值推算的三變量“或”重現期設計值。作為工程設計與風險管理,盡管存在偏向安全問題,但采用R1-R6-R24組合同頻率設計暴雨值為更高安全標準的防雨洪工程設計或風險預警提供了科學依據。 表5 樣本設計值 選取1967、2013年的受臺風影響的2場典型暴雨過程進行同頻率分時段縮放。放大系數公式: K=X設計/X典型 (23) 式中X設計——不同重現期的設計降雨量;X典型——典型暴雨降雨量。 以雨峰同頻率放大法求重現期200 a(P=0.05%)R1-R6-R24三時段雨量聯合分布的設計暴雨過程線。為了比較,另推求了R1-R6和R1-R24兩變量聯合分布以及以雨峰同頻率放大的設計暴雨過程線。由圖3可見,多變量方法與單變量方法所推求的200年一遇設計暴雨過程線的比較顯示,采用R1-R6-R24組合方法推求的3個時段雨量的設計值均大于相應單一時段樣本推算的設計值,也大于采用2個時段雨量組合的設計值。可見,采用R1-R6-R24組合方法放大的過程線對流域防雨洪設計工程更安全,采用R1-R6-R24組合的設計暴雨過程線也更加符合流域水文現象的內在規律和防洪工程實際的要求。 a) 1967年 b) 2013年圖3 200年一遇設計暴雨過程線比較 按式(12)—(19)分別推算了1967、2013年典型暴雨過程的條件重現期及相應的條件概率,結果見表6。結果顯示:①等量事件發生條件下的條件重現期小于不超過事件發生下的條件重現期,出現的危險率P(超值條件概率)則大之;②1967年典型暴雨出現的4個條件重現期都分別小于2013年主峰靠前的單峰雨型的對應條件重現期,危險率則反之。其中,等于24 h雨量(419.9 mm) 一個等量事件條件下出現的重現期最小,危險率最大。這表明主副多峰雨型且主峰靠后1967年暴雨過程對于流域防洪安全具有更大的威脅。 表6 2個典型設計暴雨過程的條件重現期與危險率 因此,對于主副多峰雨型且主峰靠后的暴雨過程,由于前期降雨首先使得流域下墊面土壤水趨于飽和產生超滲產流,疊加在后期雨峰形成的坡面流將匯集形成更強的洪水過程,流域出現洪水的風險更大,是此流域防范雨洪風險的最主要類型。 本文將不同歷時雨量之間具有相關關系的暴雨過程簡化為雨峰、6 h雨量和24 h雨量三變量聯合分布,采用非對稱極值Copula構建曹江流域典型暴雨過程線,并與由2個時段和由單一雨峰的同頻率設計暴雨過程線方法進行了比較。研究結果有以下結論。 a) 采用3個歷時雨量推求的曹江流域設計暴雨值大于2個時段和單一時段設計暴雨值,由此放大的設計暴雨過程線,整體效果相對最優,對設計雨型的研究方法提供了新思路。由得到的典型設計暴雨過程線推算的流域洪水過程更符合流域水文現象的內在規律和防洪工程的實際要求。 b) 按24 h最大雨量選取的2013年的單峰雨型與1967年的主副多峰雨型都具有較高代表性。但與2013年主峰靠前雨型比較,主峰靠后的1967年的暴雨過程危險率更大,對流域防洪安全具有更大的威脅,構建的典型設計暴雨過程線更具代表性。 c) 1967、2013年2個典型年的R1-R6-R243個時段雨量聯合分布的“或”聯合重現期都小于單一時段雨量重現期,危險率最大,以多時段雨量組合的“或”聯合重現期作為流域的設計標準,對于應對此流域雨洪風險更合適。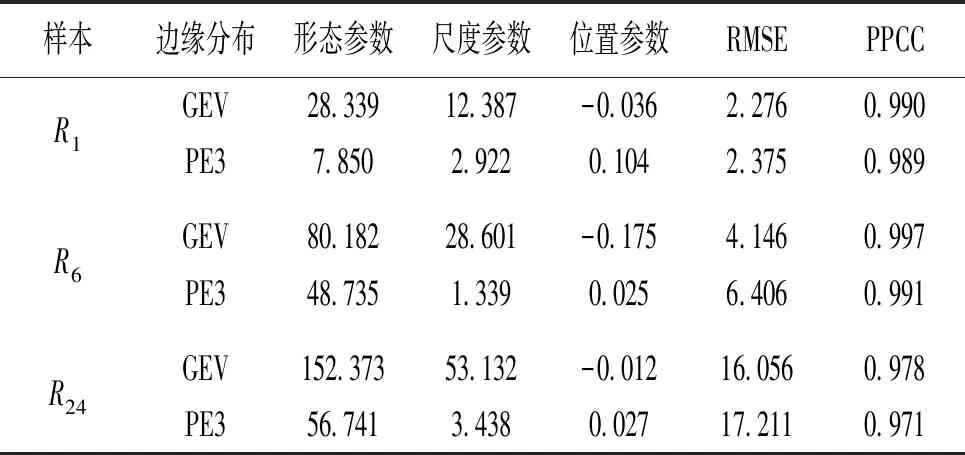
2.3 典型暴雨過程線選擇
2.4 同頻率法推求設計暴雨過程線
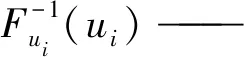
2.5 設計暴雨過程線的條件重現期及危險率

3 結論

