基于簡化實頻法的寬帶匹配電路實驗教學研究

劉國華，周國祥，郭燦天賜

（杭州電子科技大學 電子信息技術國家級虛擬仿真實驗教學中心，浙江 杭州 310018）

在當前5G 通信開始商用的大背景下，射頻微波專業技術人才需求旺盛。為了適應行業發展，“微波技術基礎”課程教學改革勢在必行。阻抗匹配是該課程的重要內容，其作用是將信號源的功率最大不失真地傳輸到負載，其性能對通信系統至關重要。但阻抗匹配電路概念抽象、理論性強，是公認的教學難點。

經過對多年教學效果的分析，我們對實驗環節中的阻抗匹配實驗內容進行了改革，將傳統的L 型窄帶匹配電路設計升級為與當前5G 寬帶通信相適應的寬帶匹配電路設計，將簡化實頻技術（SRFT）的科研成果引入實驗教學。

1977 年，Carlin 首先提出原始實頻法，這是一種基于線性分段近似逼近最佳特性的網絡綜合方法[1]，為寬帶匹配網絡設計提供了新途徑。1982 年，Yarman在原始實頻法的基礎上，對算法進行了改進，提出了簡化實頻算法[2]，縮短了算法優化時間，使設計更便捷。

國內陳軼鴻、何瑤、武軍偉和馬銀圣[3-8]等學者把實頻技術應用到天線的寬帶阻抗匹配上，不僅減少了由阻抗失配引起的損耗，還提高了天線的工作帶寬和饋電效率。

簡化實頻法用歸一化散射參數來描述無損耗的雙端口匹配網絡，很適合用來設計微波放大器[9]的輸入輸出匹配電路。當它與建模技術相結合時，可以為任何類型的寬帶匹配問題提供有效的解決方案。

1 簡化實頻法（SRFT）理論分析

匹配電路性能通常用傳輸功率增益（TPG）來衡量。TPG[10]的定義是負載輸入功率與源輸出功率的比值，可以用來描述匹配網絡的損耗程度。圖1 是用散射參數表示的匹配網絡E。

圖1 散射參數的匹配網絡

任何有界實反射系數E11(s)可由以純電阻為終端的無耗雙端口網絡來實現，一旦求出E11(s)，即可確定網絡E的參數。因此實頻法將匹配網絡E用s參數表示為：

其中，n代表網絡中的元件數。h(s)與g(s)均是n項的赫爾維茲多項式。

根據無耗網絡特性，滿足如下條件：

最后得出TPG 的表達式為：

其中，EL為負載網絡輸入反射系數。

最后是構造誤差函數Terr(s)，使其在整個頻段內優化到一個最小值，得到優化后的h與g構建寬帶匹配電路：

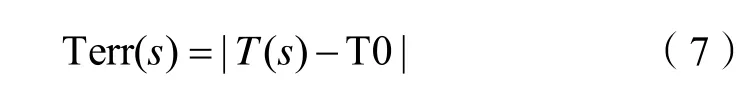
式中，T表示TPG 值，T(s)為待優化的TPG 值，T0為目標TPG 值。整個實頻算法的流程如圖2 所示。這個算法可以由MATLAB 編程實現。

該算法的MATLAB 主程序如圖3 所示。需要學生在使用該算法前，提前預設目標，包括目標TPG、迭代優化次數、優化頻段范圍、初始待優化的h等參數。

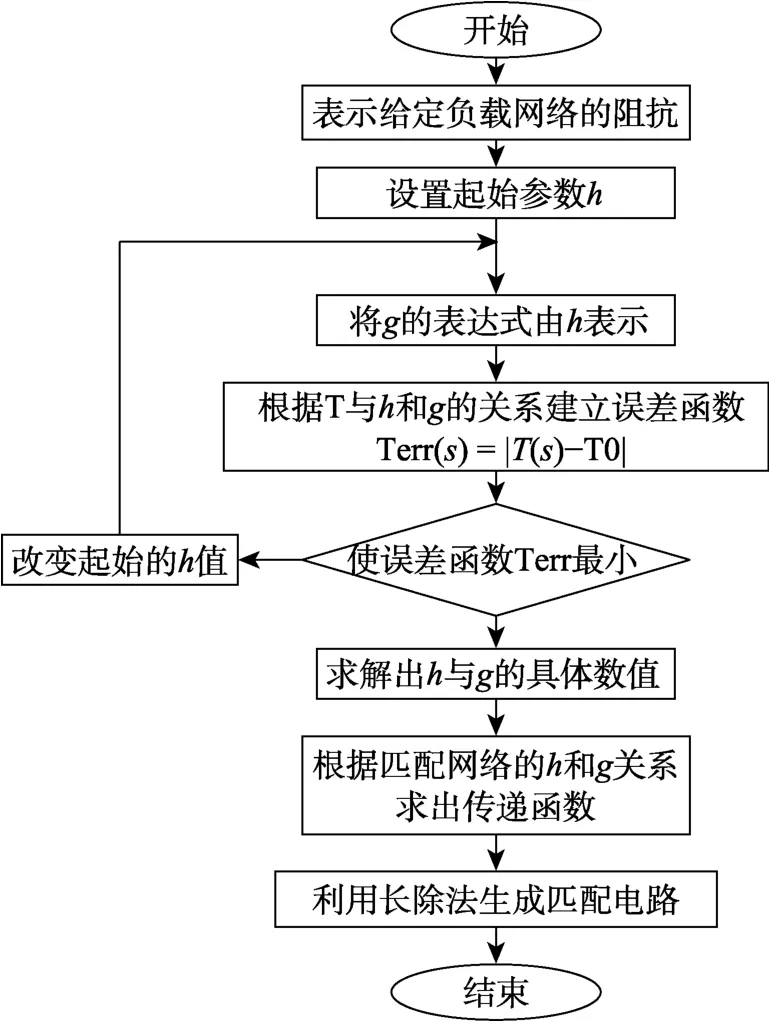
圖2 簡化實頻算法流程圖

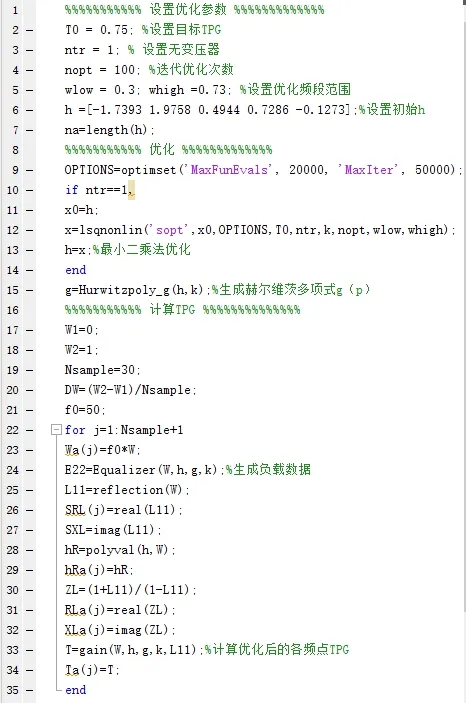
圖3 MATLAB 程序圖

2 簡化實頻法（SRFT）寬帶匹配電路設計

作為例子，對圖4 所示的負載網絡進行寬帶匹配電路設計，并將TPG 優化到期望值。

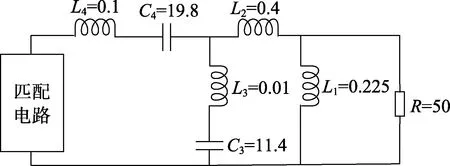
圖4 負載網絡結構

根據簡化實頻法理論分析，得出赫爾維茲多項式的表達式后，將匹配網絡的輸入阻抗Z用長除法進行運算，最終的形式表示為：

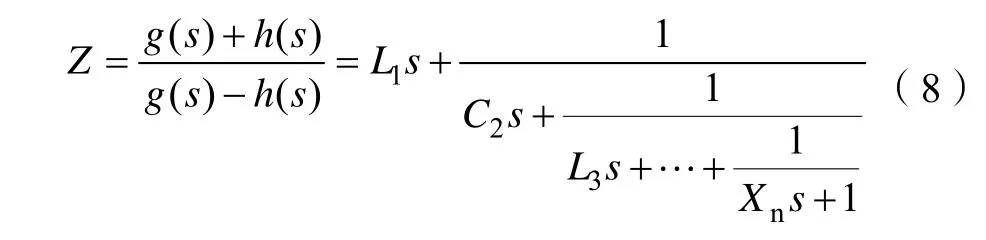
然后通過MATLAB 程序，將TPG 的預期值設置為0.75，設置中心頻率f0為50 MHz，特征阻抗為50 Ω。最終綜合出優化后的匹配電路結構如圖5 所示，TPG優化曲線如圖6 所示。

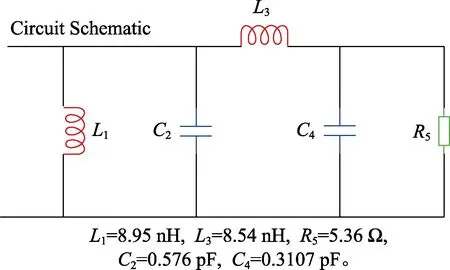
圖5 優化后的匹配電路

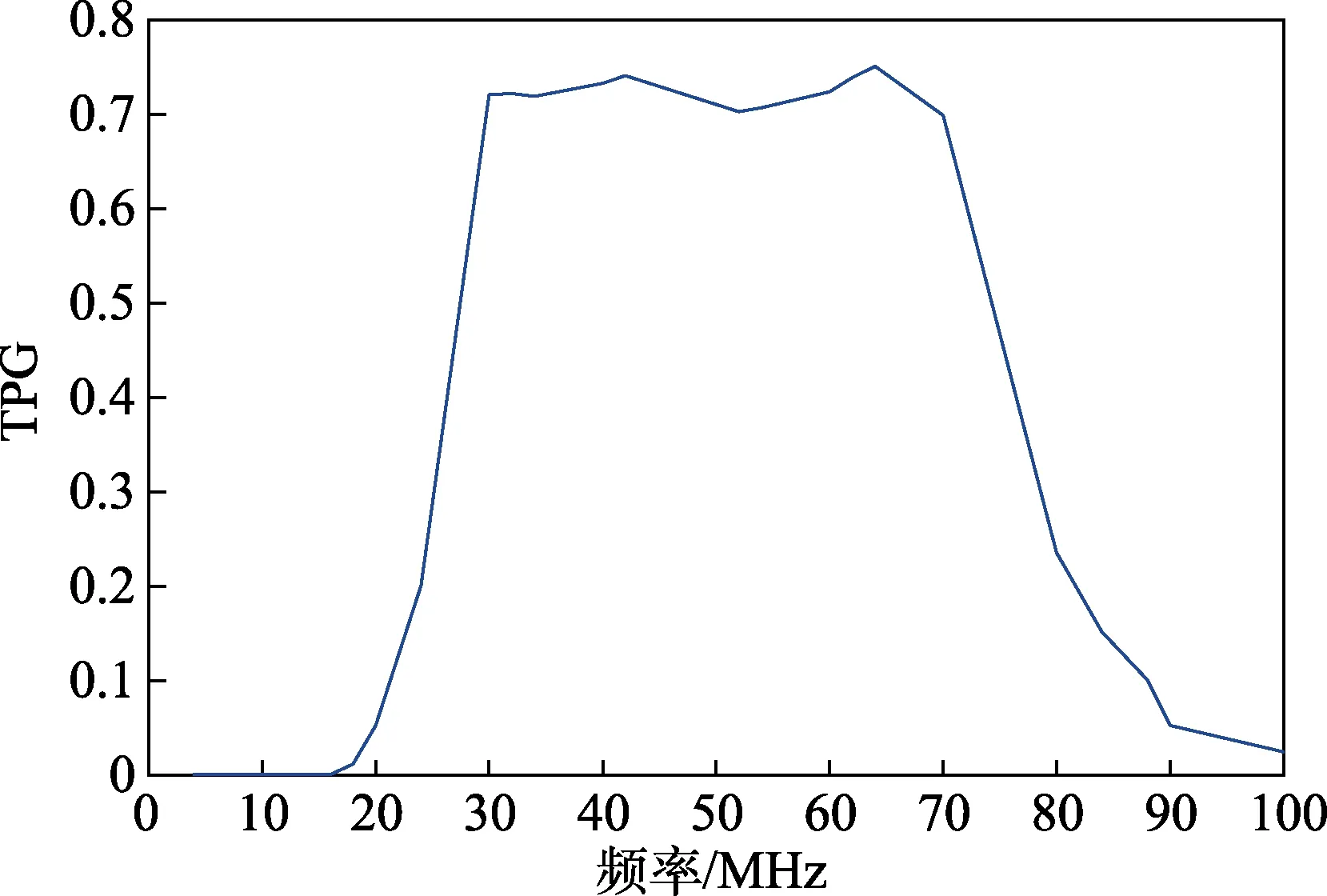
圖6 TPG 曲線圖

圖5 中顯示出的是元器件值（無單位），通過公式（10）和（11）進行反歸一化求解[11]，得到電路器件的實際值。

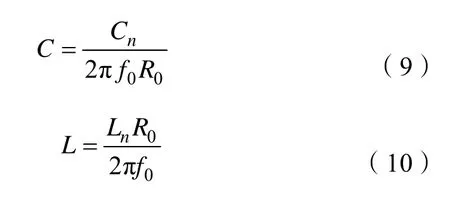
其中，Cn和Ln為優化得到的歸一化值，反歸一化后可綜合出實際電路，得到整體電路結構如圖7 所示。

為了驗證算法的有效性和所設計電路的性能，將簡化實頻法計算結果與兩款主流的射頻微波電路仿真軟件ADS 和AWR 的仿真結果進行比較，激發了學生對匹配電路設計的主動探索興趣，又能引導學生深入理解優秀仿真軟件的電路優化原理。

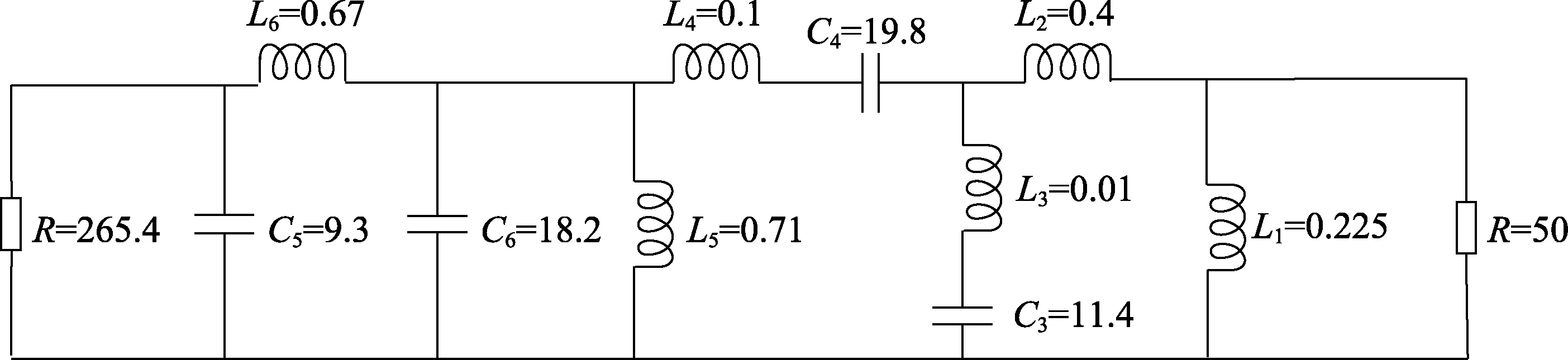
圖7 整體電路結構

3 ADS 仿真優化

將簡化實頻法中得到的完整電路在射頻電路仿真軟件ADS 中進行仿真，得出TPG 曲線；再通過ADS的優化工具進行優化，得出的結果如圖8 所示。

將優化前后的TPG 曲線進行比較，發現在頻率35～65 MHz 內，ADS 優化后的曲線值略低，優化前后的波動程度近似且穩定；在頻率25～35 MHz 內，ADS優化后的曲線波動較大，最高值達到0.76，明顯高于優化前的曲線值。而在其他頻段內，ADS 優化前后變 化不大，近似相同。因此，ADS 優化可以達到簡化實頻法優化的效果。但是從整體曲線來看，優化前TPG的波動范圍在0.7±0.01，優化后TPG 波動為0.7±0.05，有所變大，因此簡化實頻法在穩定性方面更出色。

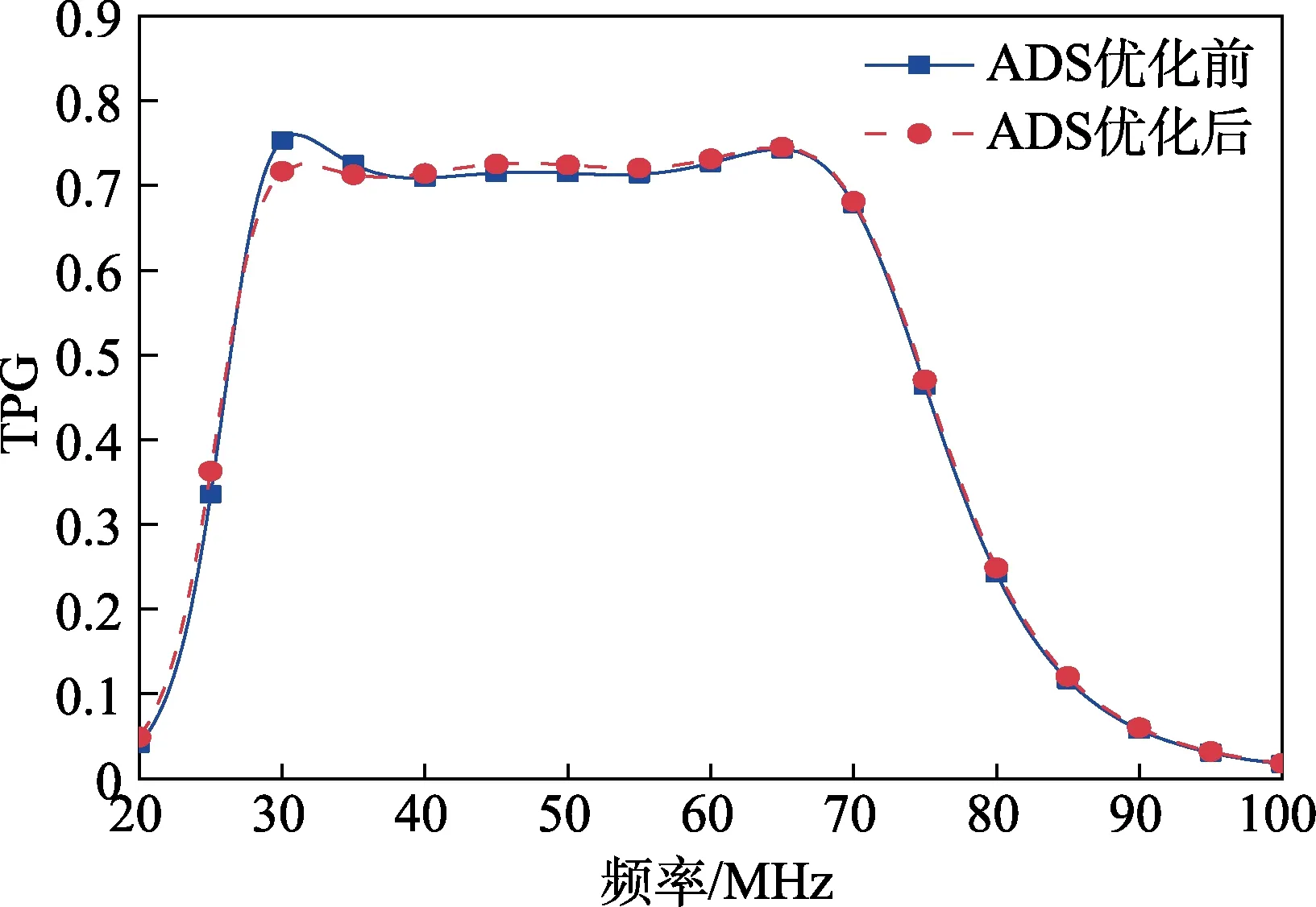
圖8 ADS 中優化前后的TPG 曲線

4 AWR 仿真優化

通過AWR 軟件自帶的優化工具優化后，將得到的TPG 曲線和簡化實頻法獲得的TPG 曲線在同一圖中進行比較，如圖9 所示。

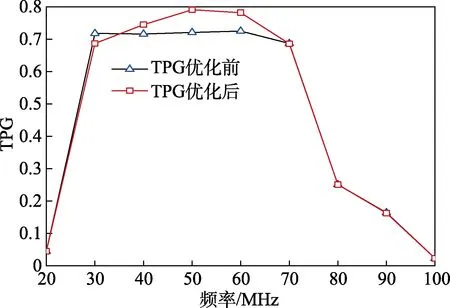
圖9 AWR 中優化前后的TPG 曲線

從圖中可以看出，在頻段35～70 MHz 內，AWR優化后的曲線值明顯增加且波動較大，最大值接近于0.8。而在頻段30～35 MHz 內，優化后的值略低于優化前。對比顯示，AWR 優化后TPG 波動較大，呈現出不穩定性。

5 三種優化方法對比

本文所選的三種優化方法分別是簡化實頻法中的最小二乘法（least squares）優化、ADS 中隨機方式（random）優化、AWR 中共軛梯度方式（conjugate gradient）優化。

其中，簡化實頻法中的最小二乘法[12]是使待優化參數和目標參數的差值平方和最小，從而實現數據的最優化。ADS 中隨機方式優化不需要使用任何數學模型來代入優化參數，通過隨機迭代數值，尋找符合目標的解。如果在不要求效率的情況下，隨機優化算法可以通過無數次的迭代優化找到最優解。但為了保證一定的效率，實驗中使用了迭代次數為50 的隨機優化作為參考對比。而AWR 中的共軛梯度優化方式具有較快的優化速度，且具有較高的穩定性。

將三種優化方式的TPG 曲線放在同一圖中進行比較，如圖10 所示。

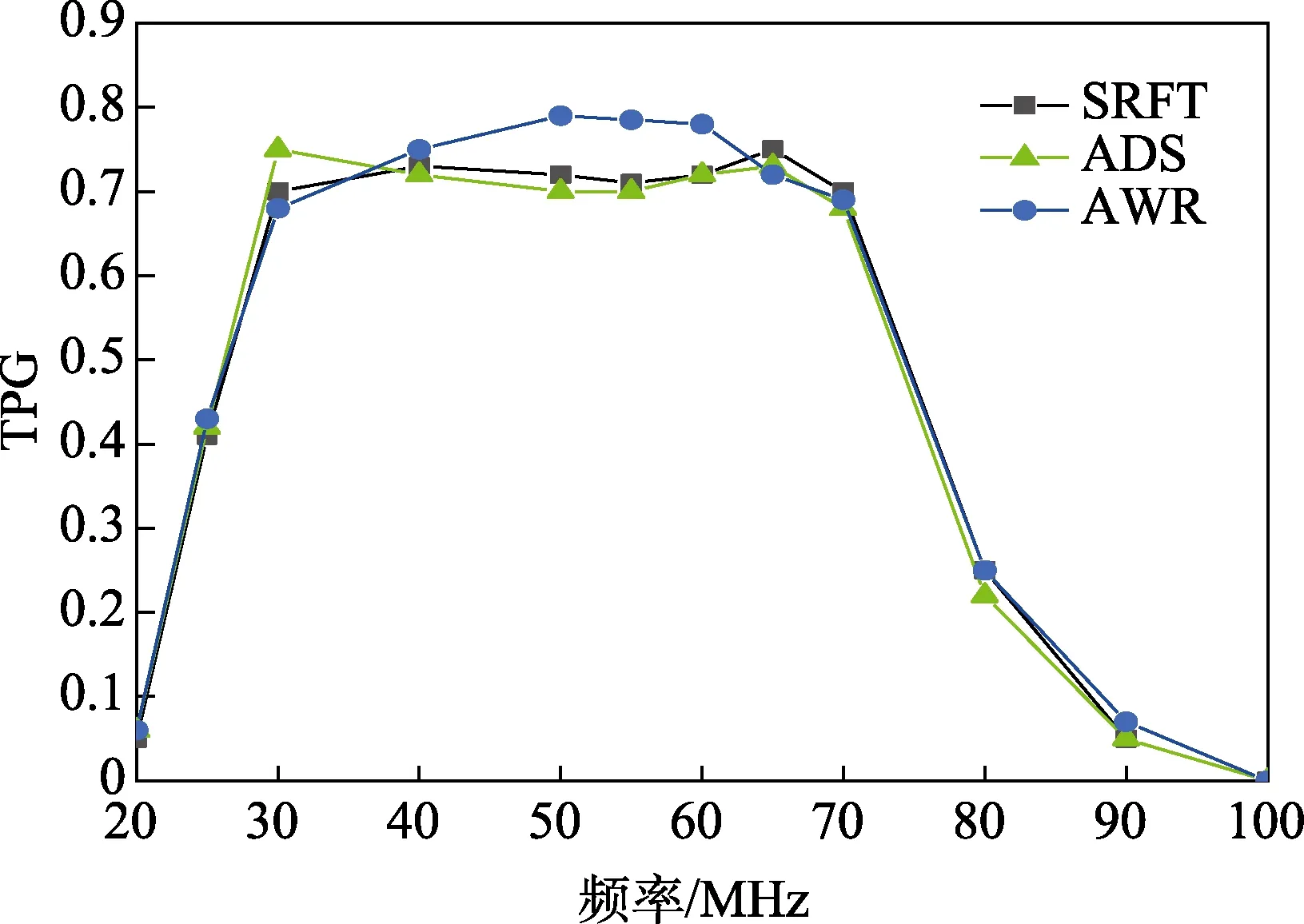
圖10 三種優化曲線對比

從圖中看出，在頻率20～30 MHz 和75～100 MHz兩個范圍內，三種曲線基本一致。而在30～75 MHz 范圍內，三種曲線呈現了不同的趨勢。ADS 優化曲線穩定在0.7，AWR 優化曲線最高值達到了0.8，而簡化實 頻法優化曲線在0.7 與預期值0.75 之間波動，最高值達到了預期值0.75。總體而言，簡化實頻法優化后的TPG 曲線在通帶范圍內比較平穩，波動最小，說明該算法與ADS 和AWR 自帶優化算法相比，對TPG 的優化效果最好。

從所用時間看，簡化實頻法、ADS 法、AWR 法分別為0.65 s、6 s 和0.34 s。由于ADS 中進行了50次迭代的隨機方式優化，其優化所需時間最長，而AWR 中共軛梯度優化比簡化實頻法快0.31 s，但其優化的TPG 曲線在帶寬范圍內波動較大，不能保證優化的穩定性。以上對比分析表明，使用簡化實頻法設計匹配電路可以得到性能與預期近似且穩定的電路結構。

6 結語

本文將科研成果引入實驗教學，用一個寬帶匹配網絡的設計實例，比較了簡化實頻法、ADS 軟件、AWR軟件的設計優化過程及結果，驗證了簡化實頻算法的有效性。由于專業仿真軟件內嵌的優化過程不可控，學生在使用時往往知其然而不知其所以然，在實驗教學中有局限性。通過自主編寫程序設計匹配網絡，能夠使學生深入體會寬帶電路設計的難點及用網絡綜合法解決問題的高效性，通過改進傳統方法解決現實問題，培養了學生的創新思維和實踐能力。