一道耐人尋味的期終學業聯考題

浙江省紹興市柯橋區平水鎮中學 封 萍 沈岳夫 312050

數學家哈爾莫斯說過“問題是數學的心臟”.對問題進行研究是教師的一項基本功.通過研究，挖掘其隱含的問題的本質，獲得豐富的教學資源.這樣做，不僅提高教師自身的專業素養，還有利于開闊學生的思路，培養學生的創新能力.本文以2020年1月柯橋區八年級數學期終學業聯考試卷中的一道選擇題目為例，做一些探索.

1 試題呈現

題目 我國古代偉大的數學家劉徽將勾股形（古人稱直角三角形為勾股形）分割成一個正方形和兩對全等的直角三角形，得到一個恒等式.后人借助這種分割方法所得的圖形證明了勾股定理，如圖1所示的矩形由兩個這樣的圖形拼成，若a=3,b=4，則該矩形的面積為（ ）.

圖1

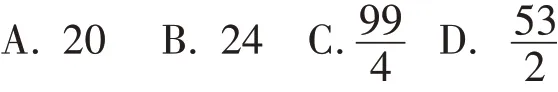
本題源于2018年溫州市中考數學試題中的第10題，此題是以數學歷史為背景，直角三角形為依托，主要考查了全等三角形、角平分線及勾股定理等知識點，綜合性較強.在閱卷后，筆者分析試卷發現此題得分率不高，這引起了我的思考，該題如何解？如何尋找解題的關聯點？筆者愿以此文與各位同仁探討.

圖2

2 解法探尋

為方便后面表述，我們先標上相關字母.如圖2，根據題意，易得CG=CF=3,AG=AE=4,AC=7,AB-BC=1，CO平分∠ACB，AO平分∠CAB，O為△ABC的內心，設正方形BEOF的邊長為x，等等.

思路1 運用勾股定理，借力整體思想

解：根據題意知，在Rt△ABC中，AB2+BC2=AC2，即(3+x)2+(4+x)2=72，整理得x2+7x=12，而矩形ABCD的面積＝(3+x)·(4+x)=x2+7x+12＝24，所以應選B.

評注：此解法先運用勾股定理得方程，再借力整體思想求得答案，這樣處理的優點是避免了方程根的求解，繁雜的計算，顯得簡捷、明了.

思路2運用勾股定理，巧借乘法公式

解：因為AB2+BC2=AC2=72，AB-BC=1，我們若巧用這個乘法公式x2+y2=(x-y)2+2xy的變形，則該矩形的面積=AB·BC=應選B.

評注：在乘法公式學習時，常常會遇到a2+b2=(a-b)2+2ab，a2+b2=(a+b)2-2ab等這些乘法公式的變形.若考生能把平時積累的這些“式”與本題的“形”有機關聯起來，那也是一種不錯的解題方法.

思路3運用勾股定理，活用AB-BC=1

解：因為AB2+BC2=AC2=72，AB-BC=1，設BC=a，則AB=a+1，所以a2+(a+1)2=72，整理得a2+a=24，而矩形的面積＝a(a+1)＝a2+a＝24，所以應選B.

評注：此解法正是抓住AB-BC=1這個隱含條件，類同思路1而獲解.這真是思之愈深，解之愈捷.

思路4抓住三角形內心，巧用面積公式

解：我們都知道有個定理：直角三角形的面積等于內切圓在斜邊上的切點分斜邊所成的兩線段的乘積.即：已知如圖3⊙O為Rt△ABC的內切圓，D、E、F分別為AB、AC、BC邊上的切點，則S△ABC=AD·BD.如圖2，根據題意，因為O為△ABC的內心，G為斜邊AC上的切點，顯然可巧用這個公式直接秒殺，所以S△ABC=AG·CG=3×4=12，進 而 可知矩形的面積＝2S△ABC=24，故應選B.

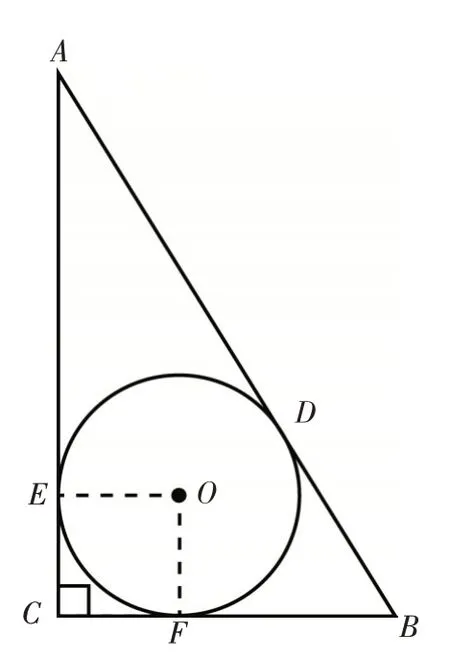
圖3

評注：此題是借用面積公式直接秒殺.由此可見，考生可以通過自己的自學、吸收、內化，積累這類先進的“武器”，為尋求解決問題的方法貯存能量.

思路5切換視角巧轉化，運用同一法求解

解：（視角1：矩形和其內部的圖形）由圖2易 知4S△AEO+4S△CFO+2SBEOF=S矩形ABCD，即理得x2+7x=12，以下同解法1.

（視角2：△ABC和其內部的圖形）由圖2知，連結BO，易知S△BCO+S△ABO+S△ACO=S△ABC，整理得x2+7x=12，以下同解法1.

評注：此題的兩種解法都是從總量等于分量之和的視角入手，即同一個圖形的面積用兩種表示法而獲解.當然，這需要考生靜下心來，認真審題，多方聯想，多方檢索，做到眼中有“形”，手中有“數”，心中建“模（面積）”，則解法自然來.

思路6重組圖形結構，融推理于計算

解：（視角1：將矩形內的圖形重拼）根據題意，用分割所得的一個小正方形和兩對全等的直角三角形重新構成如圖4的圖形，顯然，所構成的矩形ABCD與原矩形是全等的，顯然，而S′=ab=12，所以原矩形的面積S=2S′=24，故應選B.

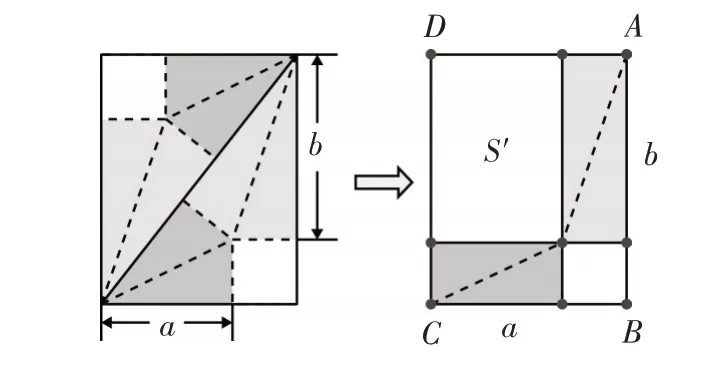
圖4

（視角2：將矩形裁剪旋轉重拼）將△ACD繞點C逆時針旋轉90°得到如圖5，連結AA′，因為AC=7A′作A′H⊥AB于點H，則AH=1，則A′H2==48.5，則原矩形面積=48.5-24.5=24，故應選B.

評注：所謂重組圖形結構就是根據圖形結構特點，適當對圖形進行剪拼（如圖4）或重新組合（如圖5）來解幾何題的一種方法.當然運用此法不僅需要具備解答基本幾何圖形的基本功，更重要的是還要有識圖、分割、拼湊、平移、旋轉以及重新組合圖形的能力.若一旦掌握，則常常會產生一種“柳暗花明又一村”的解題意境.

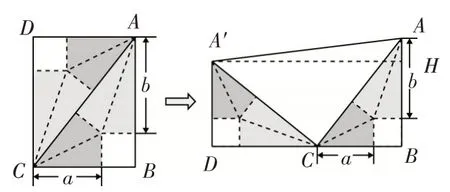
圖5

思路7探尋知識關聯，創新思維視角

解：用兩個原矩形進行重新拼圖如圖6，則可得到“弦圖”，即四邊形ACDE與四邊形GFBH均為正方形.由圖易知AC=7，

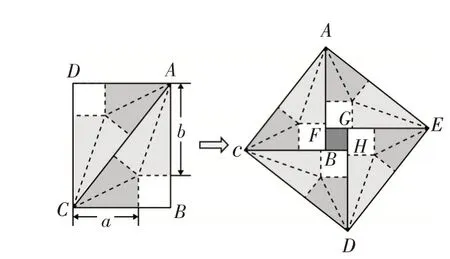
圖6

評注：此題的解法是將圖形補成定理的圖形或其他一些基本圖形，是一種重要的解題經驗，也是添加輔助線的一種重要策略.通過進一步思考，如果從圖形的結構出發、聯想，則可以將原圖補成圖6，得到“弦圖”（兩個正方形有共同的中心），從而獲解.由此看出，這種“補形”策略，是通過對題目的深入分析，或聯想，或轉化，挖掘知識模塊內蘊的思想方法，是一種經驗的“噴薄”.讓人不禁感嘆，幾何構造之神奇，探索無止境.

通過對這道選擇題的研究，筆者得到了一些啟發：如何讓考生把平時積累的幾何模型能在考場中迅速“釋放”出來，值得一線教師探究.如文中所舉的7種思路9種解法，盡管沒有固定的“模式”可以套用，但不是“憑空臆造”，而是如何化“陌生”為“熟悉”的基本圖形，并運用基本圖形分析法進行解題.由此可見，解題時如果能從多個角度思考、聯想問題，將有助于我們鞏固知識，掌握方法，以達到擺脫題海，事半功倍之效.因此，作為一線教師在平時的課堂上要把常規的解法教給學生，使學生打好扎實的基礎，與此同時，教學中也應該打開思路，多發問，多根據題目問題需要提出合理的目標或適當的變式，使學生在尚未形成固定和完善的思維方式時，充分調動學生的思維積極性和主動性，去思考問題，進而產生不同的想法和解法，從中找到符合自己的認知特點的“自然解法”.