鋼筋混凝土構件銹蝕開裂與銹脹力分析

胡志堅, 夏雷雷, 程 晨, 李柏殿, 許 兵

(1. 武漢理工大學 交通學院，武漢 430063； 2.中國建筑第六工程局有限公司，天津 300457；3. 江西省高速公路投資集團有限公司， 南昌330000)

鋼筋混凝土構件中混凝土與鋼筋間良好的粘結性能，是保證兩者協同工作的前提. 鋼筋銹蝕會造成粘結性能失效，大大降低了結構使用性能[1]. 因此對銹蝕梁的研究一直是混凝土結構的重要課題[1]. 針對鋼筋混凝土的銹蝕膨脹行為，國內外學者進行了大量的研究工作. 在試驗研究方面，文獻[2-4]在混凝土試件中預留孔洞，通過在孔洞內施加液壓模擬鋼筋均勻銹蝕的銹脹壓力，研究了銹脹力與混凝土開裂的關系及其影響因素、建立了相應的經驗公式. 理論分析方面，文獻[5-8]采用彈性力學、斷裂力學等力學方法，提出了混凝土開裂的單層或雙層圓筒模型，從理論角度對鋼筋混凝土的銹脹開裂進行了力學分析，對銹蝕深度、應力之間的關系進行推導. 在數值模擬方面，文獻[9-11]建立有限元模型，通過外加均布荷載或施加位移模擬銹蝕產物的膨脹作用，對銹脹開裂行為進行了非線性數值分析.

上述鋼筋銹脹的研究成果為鋼筋混凝土構件的耐久性設計提供了有力的技術支持，但由于銹脹開裂機理的復雜性和測試手段的局限，現有研究關于銹脹力預測的差異較大，且僅適用于根據自身研究設定的特定條件. 針對以上問題，本文在數值分析與試驗對比研究的基礎上，考慮受拉混凝土的應變軟化和塑性損傷行為，模擬了鋼筋混凝土均勻銹蝕時的銹脹開裂，對裂縫損傷發展、銹脹力的變化過程，以及銹脹應力的分布進行研究. 參數化分析了保護層厚度、鋼筋直徑、混凝土強度的影響，建立銹脹力計算公式，并通過對比分析驗證了其精度與可靠性.

1 銹脹開裂機理

鋼筋銹蝕產物會產生2～4倍體積膨脹[12]. 銹蝕產物首先會填充鋼筋和混凝土之間的空隙，根據文獻[13]的研究，該空隙寬為0．012 5 mm左右. 銹蝕產物充滿空隙后，鋼筋繼續銹蝕膨脹，而混凝土會限制它的膨脹，因此在接觸面上會產生法向壓力，稱之為鋼筋銹脹力，如圖1所示. 同時銹脹力引起鋼筋外圍混凝土產生環向拉應力. 隨著鋼筋銹蝕程度加深，銹脹力越來越大，環向拉應力超過混凝土的抗拉強度，混凝土便會開裂.

圖1 鋼筋混凝土銹脹示意圖

Fig.1 Schematic of corrosion expansion of reinforced concrete

關于銹脹開裂過程，大致可分為以下3個階段[13-15]：1)自由膨脹階段. 銹蝕產物逐漸填滿鋼筋和混凝土間的空隙，期間無銹脹力；2)混凝土受力階段. 銹蝕物充滿空隙后，混凝土開始受到徑向壓力，并隨著銹蝕增加而增大，但混凝土仍處于彈性階段還未開裂；3)混凝土開裂階段. 銹脹力不斷增加，混凝土內部開裂并不斷發展，最終延伸到表面使得裂縫貫穿混凝土，混凝土完全開裂甚至剝落.

2 有限元模型

實際的銹脹開裂過程非常復雜，諸如鋼筋非均勻銹蝕，混凝土的強度受銹蝕產物的影響等. 本文重點研究保護層混凝土的開裂過程、銹脹力均值的變化及其峰值，而鋼筋是否均勻銹蝕對此的影響并非主要因素. 因而為了簡化分析，假設銹蝕在各個方向是均勻的，混凝土強度均勻且性能穩定. 各條件沿鋼筋軸向不變，鋼筋銹蝕膨脹可以按平面應變問題處理，通常采用溫度膨脹方法模擬鋼筋銹蝕產物的體積膨脹作用[16]. 此外由于有限元手段的局限性，不考慮自由膨脹階段.

2.1 材料定義

在銹蝕分析中，銹蝕引起的環向拉應力是導致保護層開裂的主要原因，即混凝土主要是受拉破壞. 因此為準確分析混凝土的開裂行為，將混凝土材料的彈塑性變形、應變軟化效應以及混凝土的損傷考慮在內. ABAQUS提供的混凝土塑性損傷模型可以很好地模擬這些材料特性.

(1)

即得

σ=(1-d)E0ε，

(2)

受損后材料的彈性模量為

(3)

可見損傷材料的宏觀表現為彈性模量的下降，如圖2所示. 混凝土材料由于損傷引起剛度退化，在宏觀上主要表現在拉、壓屈服強度不同，拉伸屈服后材料表現為軟化，壓縮屈服后材料先硬化后軟化. 本文采用圖2所示的混凝土本構模型，模型中拉伸和壓縮采用不同的損傷因子來描述這種剛度退化.

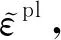
(4)

(5)

圖2 混凝土單軸受拉應力-應變曲線

(6)

(7)

本文采用現行《混凝土結構設計規范》[19]中推薦的混凝土應力-應變關系，按混凝土強度選取參數，計算對應的應力-應變曲線，代入上述公式中，求出損傷因子d. 至此便可獲得混凝土的損傷因子及其他參數. 對于鋼筋材料，由于應力值較小,始終處于彈性階段，簡單定義為理想彈性模型,材料參數參照HRB400鋼筋選用.

2.2 驗證模型

文獻[2]采用試驗方法，澆筑邊長150 mm的混凝土空心立方體塊，在孔洞內部施加液壓模擬鋼筋均勻銹蝕的銹脹壓力，對保護層的脹裂進行了試驗．

本文采用ABAQUS對其中孔洞位于一般邊位置(非角區)的5個模型進行數值模擬，模型尺寸、保護層厚度、鋼筋直徑、混凝土抗拉強度與文獻[2]相同．設置鋼筋材料溫度線膨脹系數1.2×10-5℃，再對鋼筋單元施加溫度場使鋼筋升溫膨脹，以此模擬試驗對孔洞的液壓．鋼筋和混凝土單元均為8節點平面應變單元CPE8，經計算，當單元平均邊長為2 mm和1 mm時，結果相近，滿足計算精度要求，最終網格按2 mm進行劃分.

其中一個的試驗和有限元模型如圖3所示. 5個模型的最大銹脹力的計算值與試驗值見表1．可以看出，數值計算結果與試驗結果比較吻合，最大誤差為10.2%，但應力差值不到0.8 MPa，說明本文建模方法可行.

(a)試驗模型 (b)有限元模型

Tab.1 Comparison of maximum pressure between calculated result and experimental value

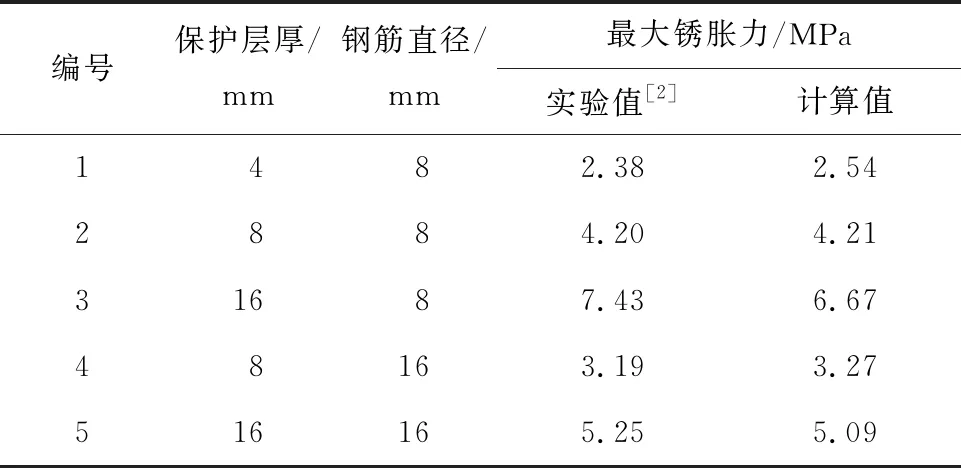
編號保護層厚/mm鋼筋直徑/mm最大銹脹力/MPa實驗值[2]計算值1482.382.542884.204.2131687.436.6748163.193.27516165.255.09

2.3 分析模型

文獻[2]的模型保護層厚度偏小，在實際結構中并不常見，因此本文采用截面為200 mm×200 mm混凝土矩形，建立二維平面應變模型，在滿足保護層與其他邊厚度差異的前提下又避免了單元數過多使計算困難的問題. 保護層厚度為30 mm，鋼筋為直徑12 mm的光圓鋼筋，位于矩形的中下方. 混凝土材料參數按C50選取，其余同上.

3 開裂過程及應力變化

3.1 開裂過程分析

圖4(a)中鋼筋附近的混凝土先出現均勻損傷，當某一單元的拉應變率先超過應力曲線的峰值，隨著變形(應變)增大，應力快速下降，損傷增加. 產生應力重分布，損傷單元釋放的應力會沿著垂直于拉應力方向傳遞給下一個單元. 數值模擬中這一過程會逐步循環迭代，直到達到某一平衡狀態. 至此，裂縫形成并向外擴展.

開裂后當Δd=0.009 3 mm時保護層一側的豎向裂縫開始加快發展，如圖4(b)所示；當Δd=0.010 9 mm時裂縫貫通，保護層完全開裂如圖4(c)所示. 隨著銹蝕增加，保護層上的裂縫進一步增大，混且凝土內部其他方向的裂縫也有不同程度的開展，如圖4(d)所示. 值得注意的是，在圖4(b)中裂縫尖端距離表面還有一定距離時，保護層表面也出現了損傷裂紋，由外向內部發展. 即在保護層裂縫完全貫通前，混凝土表面會先出現損傷裂紋，文獻[20]數值分析中亦出現了相同現象. 分析其原因是與變形有關，因保護層一側相對薄弱，隨鋼筋膨脹和混凝土內部開裂而凸出，使得保護層表面因變形而先開裂.

圖4 裂縫開展過程

在保護層裂縫貫通前后，沿保護層豎向裂縫各單元的主拉應變變化過程如圖5所示，銹脹初期鋼筋附近的混凝土拉應變較大，保護層表面混凝土的拉應變趨近于0；在裂縫貫通之前(Δd=0.009 3 mm)保護層表面的應變開始加快增長，混凝土表面出現損傷裂紋；在保護層開裂后(Δd=0.010 9 mm)，拉應變的增長主要發生在靠近保護層表面的單元，而鋼筋附近的應變增長相對較小．

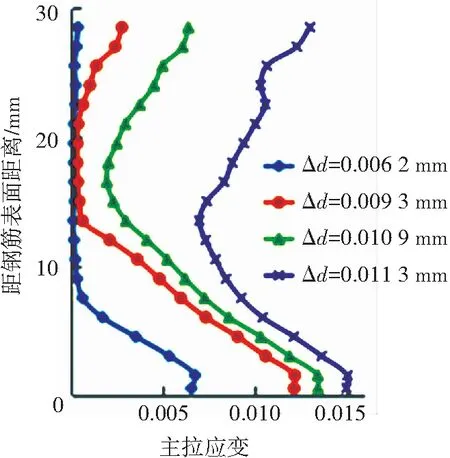
圖5 開裂前后裂縫單元主拉應變

圖6為開裂后保護層各單元的應變變化情況．開裂后期保護層各單元應變整體增大，鋼筋銹蝕率較小時(Δd=0.010 9 mm)，裂縫寬度值比較小，各單元的應變變化梯度不大．隨著鋼筋銹蝕率的增長，鋼筋表面位置處的裂縫寬度逐漸增大，各單元應變變化梯度也越來越明顯，靠近保護層表面的應變增幅明顯大于鋼筋處的混凝土應變．

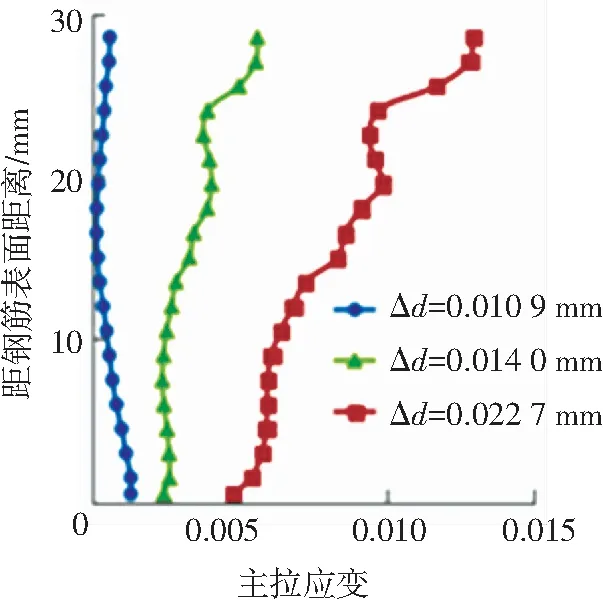
圖6 開裂后裂縫單元主拉應變

3.2 銹脹力環向分布分析

分析不同銹脹程度下，與鋼筋接觸的孔邊混凝土圓周上各部分銹脹應力的分布，可以對銹脹過程有更全面的認識.

圖7為不同銹蝕程度下鋼筋周圍法向應力分布．可以看出在銹蝕初期(Δd=0.003 9 mm)鋼筋周圍各部分銹脹力大致相等，呈均勻分布．隨著銹蝕加劇(Δd=0.005 8 mm)銹脹力分布變得不再均勻，當Δd=0.008 4 mm時應力分布明顯出現鋸齒狀. 隨著銹脹進一步增加，鋼筋圓周上各處應力分布差異加劇，Δd=0.010 9 mm時各點處應力值差異達到10 MPa以上. 此外圖7與圖4對比發現，銹脹力分布不均勻基本與裂縫發展同步，這主要是由于混凝土內部開裂導致應力重分布所致. 以上分析說明在鋼筋銹蝕的中后期，單獨地獲得某一點處的銹脹力并不具備代表性，必須獲取多個點取其平均值才能真實地反映銹脹力的大小.

3.3 銹脹力變化過程

鋼筋和混凝土之間的粘結力，由膠著力、摩阻力和機械咬合力3部分組成[21]. 其中無論摩阻力還是機械咬合力，鋼筋和混凝土間的法向應力都會對其大小產生明顯影響. 因此，研究銹蝕過程的鋼筋銹脹力的變化，對研究結構粘結力來說是非常必要的. 選擇所有與鋼筋接觸的周邊混凝土單元，提取各單元徑向上的應力之后取平均值，得出鋼筋與混凝土單元接觸的平均徑向應力即銹脹力隨Δd的變化過程曲線，如圖8所示.

圖7 不同銹蝕程度下圓周上銹脹力分布

Fig.7 Distribution of expansive pressure with different corrosion degrees

圖8 銹脹力隨Δd的變化曲線

在初始彈性階段，銹脹力基本呈線性增長；在Δd=0.009 6 mm時銹脹力達到峰值8.26 MPa，此時裂縫并未完全貫通. 如圖4(b)所示，即銹脹力最大值在保護層完全開裂前到達. 之后保護層裂縫發展并完全貫通，應力釋放使得銹脹力快速下降，最后在Δd=0.019 6 mm時應力下降到5.39 MPa左右，銹脹力趨于穩定. 可以看出銹脹力的變化大致可以分為3個階段：上升段、快速下降段和穩定階段，而保護層開裂是銹脹力進入下降段的主要原因和重要標志. 之后混凝土內部裂縫雖然會繼續發展，但由于未出現新的貫穿裂縫，應力不會出現明顯變化，銹脹力便進入穩定階段.

4 參數分析

4.1 混凝土保護層厚度的影響

以保護層厚度c為變量，其他條件與上述c=30 mm時的工況相同，分析20、25、35、40 mm 4種不同的保護層厚度的影響. 計算結果表明保護層豎向裂縫開展過程與30 mm時類似，即保護層厚度c值的變化對保護層的損傷開裂過程影響很小. 但對于銹脹力大小的影響，則明顯不同. 圖9為不同c值下，平均正應力隨Δd的變化曲線.

圖9中各曲線的變化趨勢相同，但保護層厚度增加對銹脹力的影響顯著，主要包括以下幾點：1)銹脹力的峰值隨保護層厚度增加而增大；2)峰值出現的時間延后，峰值出現意味著保護層將完全開裂，因此保護層越厚其完全開裂所需的銹蝕率越大，此時結構越不容易銹蝕開裂；3)保護層開裂后，銹蝕后期的殘余應力越來越大.

圖9 不同保護層厚度的銹脹力曲線

Fig.9 Variation of expansive pressure for different cover thicknesses

經分析銹脹力峰值和對應的銹蝕程度均隨保護層厚度呈線性增長，即保護層厚度直接影響最大銹脹力及其對應的開裂銹蝕率.

4.2 鋼筋直徑變化的影響

保持30 mm保護層厚度及其他條件不變，僅改變鋼筋的直徑，分析鋼筋直徑的變化對銹脹力的影響. 鋼筋直徑d分別取為10、12、14、18、22 mm. 由于此時鋼筋直徑為變量，因此以直徑增量與初始直徑的比值Δd/d為參考變量，Δd/d越大表明鋼筋的銹蝕程度越高. 不同鋼筋直徑條件下銹脹力的變化過程曲線如圖10所示，保護層厚度恒定時，鋼筋直徑的增加對銹脹力的影響顯著. 隨著鋼筋直徑增加，銹脹力曲線變化存在如下明顯特點：1)銹脹力的峰值越來越小；2)峰值出現的時間提前，保護層完全開裂所需的銹蝕量變小；3)保護層開裂后，銹蝕后期的殘余應力越來越小. 鋼筋直徑增大的影響與保護層厚度減小的影響規律相似.

用c/d值表征保護層厚度c和鋼筋直徑d兩種參數對銹脹力和保護層開裂銹蝕程度的影響，結果如圖11所示，線性關系良好，說明c、d兩個參數的變化可以統一用比值c/d表征.

4.3 考慮混凝土強度的回歸公式

混凝土強度，尤其是抗拉強度對銹脹力峰值也會有直接影響. 不同標號混凝土強度的數值結果見表2.

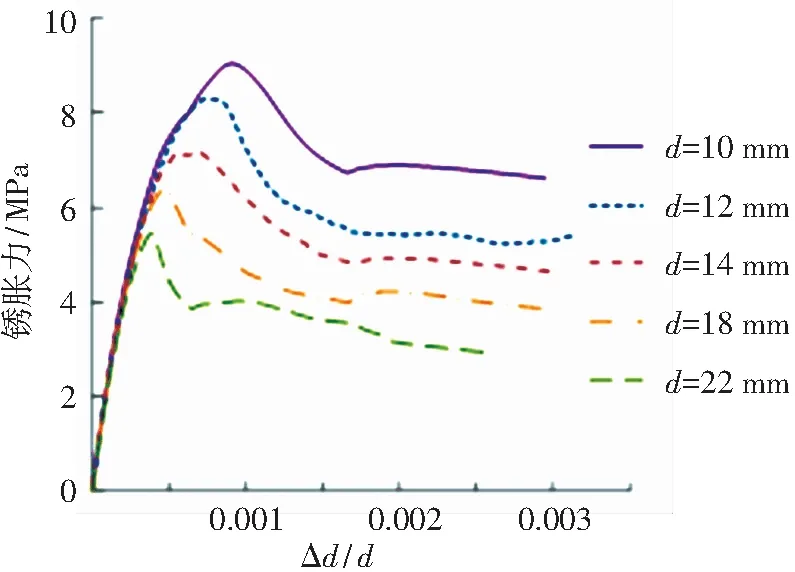
圖10 不同鋼筋直徑的銹脹力曲線

Fig.10 Variation of expansive pressure for different steel bar diameters

(a) c/d值與銹脹力峰值的關系

(b) c/d值與完全開裂銹蝕程度的關系

Tab.2 Maximum expansive pressure for different concrete strengths

混凝土標號ft/MPa銹脹力峰值/MPac/d=20 mm/12 mmc/d=30 mm/12 mmC201.544.055.80C302.015.406.96C402.406.107.67C502.656.428.30

銹脹力峰值P與混凝土抗拉強度也基本呈線性增長關系. 結合c/d分析結果，擬合出以c/d值和混凝土抗拉強度ft為參數的銹脹力峰值公式為

P=ft(0.94c/d+0.91).

(8)

利用該公式可以確定保護層開裂時的最大銹脹力. 圖12為各公式代入文獻[2]的試驗模型參數(c/d值和混凝土抗拉強度ft)的計算結果，并與試驗值比較. 除本文公式和文獻[13]、文獻[22]公式外，其他文獻公式的分析結果均與試驗值相差較大. 而文獻[13]公式結果與試驗值的最大誤差也明顯高于本文結果，文獻[22]的多項式公式能達到本文公式的類似精度，但其公式本身包含11項，使用非常麻煩，且存在保護層厚度c的平方、鋼筋直徑d的平方等各類變量的高次項，力學概念不如本文公式明確.

圖12 各經驗公式與試驗值對比

Fig.12 Comparison of empirical formulas with experimental data

5 結 論

1)針對不同厚徑比c/d條件下鋼筋混凝土均勻銹蝕時的銹脹開裂，對比研究了裂縫發展和銹脹力的變化過程.

2)在保護層開裂后，單獨地獲得某一點處的銹脹力并不具備代表性，必須獲取多個點取其平均值才能真實地反映銹脹力的大小.

3)保護層厚度和鋼筋直徑對銹脹力和保護層開裂銹蝕程度的影響呈線性關系，且可以統一用厚徑比c/d表征.

4)根據分析和計算結果，提出了鋼筋混凝土構件銹脹力回歸公式，并通過試驗數據和其他文獻提出的公式比對，驗證了鋼筋混凝土構件銹脹力回歸公式的有效性與精度.