橋梁伸縮縫跳車沖擊荷載計算方法與模型實驗

丁 勇, 王 佩, 游玖昂, 諸葛萍

(1.寧波大學 土木工程系, 浙江 寧波 315211； 2.橋梁工程結構動力學國家重點實驗室(重慶交通科研設計院), 重慶 400067)

在橋梁結構中，伸縮縫是最容易發生早期損壞的部件[1]，與伸縮縫相關的維修花費超過橋梁結構早期維護費用的20%[2]. 伸縮縫早期損壞的重要原因是載重汽車輪胎的長期沖擊作用，這個沖擊荷載也是伸縮縫設計的主要參數. 遺憾的是，目前該沖擊荷載的確定還缺乏明確的理論與實驗依據，世界各國的取值差別也很大. 中國伸縮縫設計指南[3]以140 kN作為車輛的標準軸重，并考慮0.45的沖擊系數；美國橋梁規范[4]以145 kN作為標準軸重，并計入0.75的沖擊系數；英國規范[5]和德國規范[6]取200 kN的車輛軸重，但沖擊系數取值不同，分別為0.5、0.4. 因此，明確伸縮縫沖擊荷載，可為伸縮縫及其周邊橋(路)面的設計與維護提供參考[7-9].

關于伸縮縫跳車沖擊荷載的實驗研究還很少，文獻[10]通過測量模數式伸縮縫在車輛作用下的動應變與動位移，推測汽車輪胎荷載豎向的沖擊系數為0.2～0.3，橫向的沖擊系數約為0.15；文獻[11]則認為0.1～0.5的沖擊系數與其實測結果比較符合. 在上述實驗研究中，由于跳車沖擊荷載大，直接測試困難，因此都是通過伸縮縫結構動力響應間接獲得車輪沖擊荷載，且都沒有計及汽車行駛的快慢、伸縮縫開口的大小等對沖擊系數的影響.

在理論算法上，往往通過分析車輛通過伸縮縫時的振動來計算沖擊荷載，其中輪底在伸縮縫上的局部脫空現象是分析的難點. 文獻[12]假設車輪通過伸縮縫時的輪底運動軌跡是長20 cm，深2～4 cm的凹臺，這個假設源于對伸縮縫的外形量測，與實際的輪底軌跡存在差別. 文獻[13]提出了一種基于分布式彈簧-阻尼單元(distributed spring-damp element，以下簡稱DSD單元)的計算方法，可以模擬車輪通過伸縮縫時的局部脫空情況，并用于計算作用在伸縮縫上的車輪沖擊荷載，但是該方法忽略了輪胎通過伸縮縫時接觸長度的變化，并且還缺乏實驗驗證.

本文在上述工作基礎上，對橋梁伸縮縫跳車沖擊荷載問題進行了算法改進和實驗研究. 首先制作了橋梁與車輛的縮尺實驗模型，實測縮尺模型在伸縮縫跳車時的車輪沖擊力. 然后改進了假設輪底運動軌跡的車輪荷載計算方法，考慮了荷載大小、輪胎和伸縮縫尺寸對輪底運動軌跡的影響. 同時，也改進了基于DSD單元的車輪荷載計算方法，考慮了車輪經過伸縮縫時輪胎-路面接觸長度的變化. 最后，對典型三軸載重汽車經過伸縮縫時的沖擊荷載進行了數值模擬，討論了伸縮縫寬度、車輛速度對輪載沖擊系數的影響.

1 模型實驗

以圖1所示的單縫式橋梁伸縮縫為例，建立縮尺模型實驗裝置. 實驗裝置的設計圖和制作完成后的照片如圖2所示. 橋梁采用1∶30的單車道鋁合金梁縮尺模型，相當于寬度為3米的橋. 橋梁模型分3段：第1、3段為引橋，第2段為簡支梁主橋. 每兩段模型連接處布置單縫式伸縮縫. 車輛模型采用1∶30的兩軸車模型，車輪用彈性橡膠制作，受壓變形后，可以反映輪胎與路面之間的接觸長度. 車輛動力由牽引電機通過鋼絲繩提供，運動路徑包含3段橋梁模型，因此可以模擬車輛通過橋梁伸縮縫時的跳車現象.

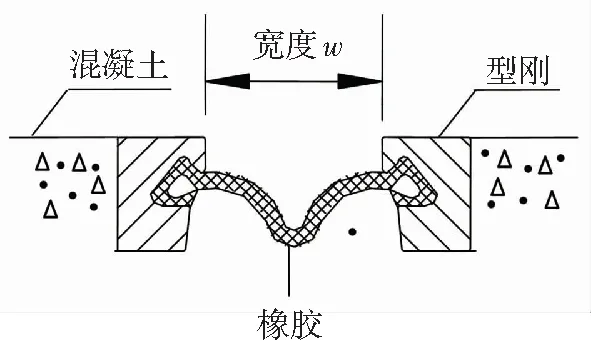
圖1 單縫式橋梁伸縮縫

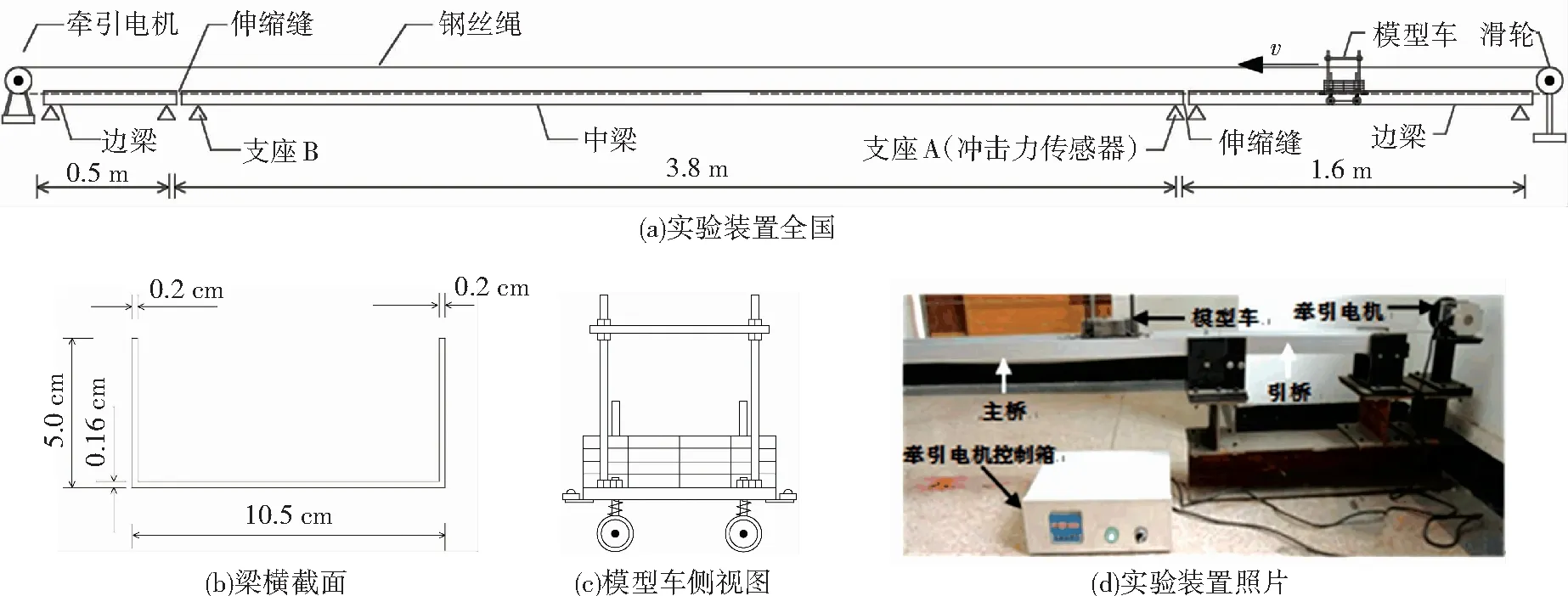
圖2 縮尺模型實驗裝置

測試系統主要是伸縮縫沖擊力測試裝置，該裝置由沖擊力傳感器和信號處理系統組成. 如圖2(a)和圖3所示，沖擊力傳感器有兩個，為美國PCB公司的200B02型石英沖擊力傳感器，代替支座A支撐簡支梁主橋，位于伸縮縫旁，直接實測車輪沖擊力導致的支座豎向支撐力. 因為作為支座A的沖擊力傳感器距離梁端只有0.5 cm，簡支梁長度達3.8 m，所以當模型車的前輪經過伸縮縫駛上中梁時，豎向支座反力之和與兩前輪沖擊荷載之和差別很小，可以認為兩者相等.

實測得到的典型沖擊力曲線如圖4所示，其中兩條曲線分別為模型車輛通過伸縮縫時兩個沖擊力傳感器測得的力，圖4對應的模型車速度為0.4 m/s，伸縮縫寬度為3 mm.

圖3 沖擊力傳感器(支座A)

圖4 車輛沖擊力實測值

在圖4中，峰值1是圖2(c)所示模型車前輪通過伸縮縫時的沖擊力峰值，峰值2是后輪通過伸縮縫時的沖擊力峰值. 因為壓電式沖擊力傳感器測得的力隨時間衰減，所以實測結果中的峰值1精度較高，反映了前輪的沖擊荷載. 實測結果中的峰值2包含了后輪沖擊荷載和前輪荷載的影響，由于前輪沖擊荷載測試值的衰減，所以峰值2的精度受到干擾，不宜用于分析車輪的沖擊荷載.

由于實驗誤差，圖4中的左前輪和右前輪的沖擊力略有不同，因此本文取兩者的平均值作為前輪的平均沖擊力，這也和下文采用二維的車輛模型計算伸縮縫沖擊荷載相一致.

2 計算方法

實測得到的車輪沖擊力可以用來檢驗對應的計算方法，此時通過對車輛在伸縮縫上的動力響應進行有限元分析，得到車輪的沖擊荷載. 以縮尺模型實驗中的小車為例，如圖2(c)所示，相應的二維有限元模型，如圖5所示，包含7個節點，6個單元. 其中車體用剛性梁單元模擬，車體懸掛系統用彈簧-阻尼單元模擬[14]，對應于不同的計算方法，彈性車輪分別選用彈簧-阻尼單元或分布式彈簧-阻尼單元來模擬[15].

通過對模型車輛的實測，得到圖5所示車輛有限元模型的計算參數.l1為0.05 m，h1、h2分別為0.013、0.054 m，m1、m2分別為4.35、0.125 kg，J1為0.007 9 kg·m2. 由壓縮試驗得到輪胎剛度k1為53.4 kN/m，由自由振動衰減曲線測得輪胎阻尼c1為61.4 N·s/m. 由于輪胎以上部分為鋼結構，其支撐剛度遠大于輪胎剛度，因此k2取為遠大于k1的常數，阻尼c2則取為遠小于c1的常數.

圖5 試驗小車的有限元模型

經過單元組集，獲得模型車的振動方程組為

(1)

其中：uv為節點位移向量；Mv、Cv、Kv分別為質量、阻尼、剛度矩陣；Fv為車輛所受荷載向量；t為時間.

方程(1)用Newmark法在時域內積分求解，求解難點在于車輪經過伸縮縫時輪底局部脫空，導致輪底位移是未知量[13]. 在圖5所示的有限元模型中，1號、5號節點在車輪通過伸縮縫時的位移即為未知量. 為了確定伸縮縫上的輪底脫空段位移，本文提出了以下兩種方法.

2.1 假設輪底運動軌跡

圖6為載重車的輪胎在路(橋)面和伸縮縫上行駛時的變形情況. 由圖可見，車輪在伸縮縫外的路面上時，輪胎壓縮量為ΔR，輪胎-路面接觸長度為a；車輪通過伸縮縫時，輪底局部脫空，最大脫空長度即為伸縮縫寬度w，此時輪胎壓縮量為ΔR′，輪胎-路面接觸長度為a′. 文獻[12]假設車輪通過伸縮縫時的輪底運動軌跡如圖7所示，該軌跡來自對特定伸縮縫、在特定時間的測量，適用面不廣.

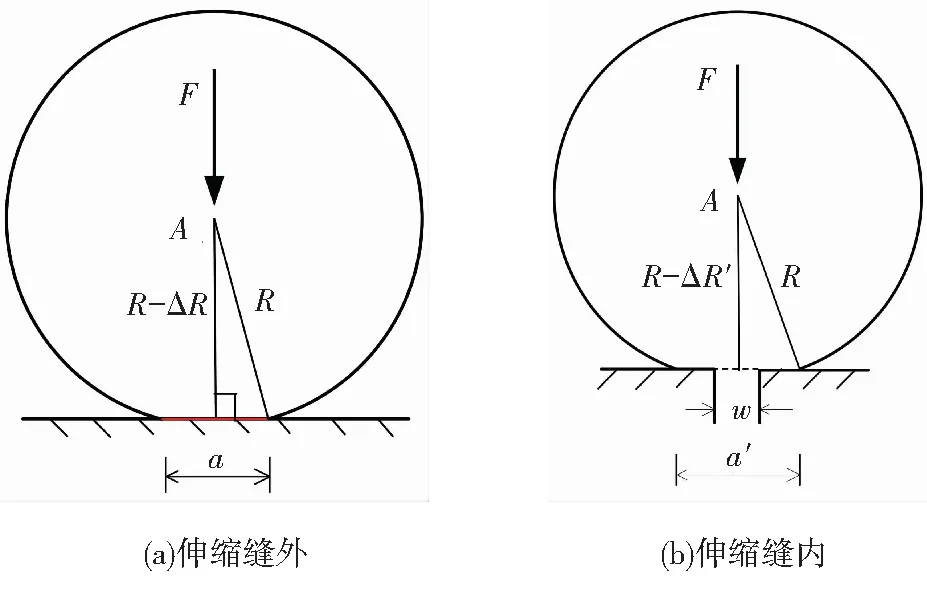
圖6 載重車輪胎變形

圖7 假設的輪底位移曲線[12]

本文對上述假設輪底軌跡方法進行了改進，考慮了輪載大小、輪胎和伸縮縫尺寸對輪底運動軌跡的影響. 如圖6(a)所示，當輪胎在普通路面上時，輪軸荷載F作用下的豎向壓縮量為

ΔR=F/K，

其中K為輪胎的剛度.

當車輪位于伸縮縫中心時，如圖6(b)所示，由于輪底局部脫空，脫空部分不受路面的支持，所以車輪的豎向壓縮量為

(2)

假定輪胎在變形前后的半徑R不變，那么圖6(b)中輪胎與地面的接觸長度為

(3)

由式(2)、(3)可得關于a′的方程為

(4)

由式(4)求得a′，再由式(3)可得輪胎在伸縮縫內的壓縮量ΔR′.

輪胎在伸縮縫內和普通路面上的壓縮量之間的差別為ΔR′-ΔR. 考慮到伸縮縫中的車輪底部局部脫空，因此車輪的實際支撐剛度減小. 但是在有限元計算模型中，輪胎單元的剛度K大小不變，因此在有限元計算中，需要將輪胎在伸縮縫內、外的壓縮量之差作折減，即

(5)

其中h為折減后的輪胎壓縮量之差.

假設式(5)所示的壓縮量之差為車輪跨越伸縮縫過程中的輪底最大位移，整個跨越過程中輪底的運動軌跡如圖8所示. 過伸縮縫前、后的輪底位移為零；在上、下伸縮縫的w長度段內，輪底位移為余弦函數；中間a-w長度段內，輪底位移保持為h.

圖8 車輪底部的運動軌跡

上述假設輪底位移是對文獻[12]假設輪底位移的改進，考慮了輪胎-路面接觸長度、伸縮縫寬度的影響，使之可以用于各種類型的車輪通過橋梁伸縮縫的情況，包括縮尺模型車輛的車輪.

2.2 改進的分布式彈簧-阻尼單元

文獻[13]曾用一種分布式彈簧-阻尼單元(DSD單元)代表汽車輪胎的力學特性，進一步分析汽車輪胎對伸縮縫的沖擊力，但是該工作假定車輪經過伸縮縫時，與路面的接觸長度保持為常數a. 由于輪胎在伸縮縫上的脫空情況，該假定會帶來一定的計算誤差. 為此，本文改進了上述分布式彈簧-阻尼單元，其結構如圖9所示. 該單元中輪胎經過伸縮縫時與路面接觸長度為a′，a′由式(3)計算. 因為伸縮縫中的車輪壓縮量ΔR′與車輪所在位置和振動位移有關，所以a′不再保持為常數.

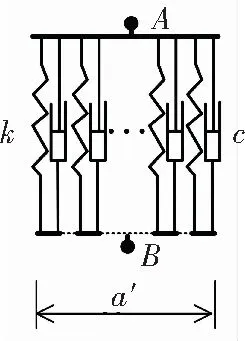
圖9 改進的分布式彈簧-阻尼單元

如圖10所示，當用改進的DSD單元所代表的汽車輪胎通過伸縮縫時，仍然分為3階段：下縫段、跨縫段、上縫段，單元底部B點的等效位移為

其中u1、u2、u3分別為輪底在a1′、a2′、a3′段的豎向位移.

(a)下縫段 (b) 跨縫段 (c)上縫段

Fig.10 DSD element of thewheel passing through the expansion joint

分布式彈簧-阻尼單元的平衡方程依舊和普通的彈簧-阻尼單元一樣[15]. 有限元分析獲得節點位移和速度后，進一步可求得輪壓荷載為

(6)

也可得到輪胎作用于伸縮縫結構a1′、a2′、a3′段的壓力分別為

(7)

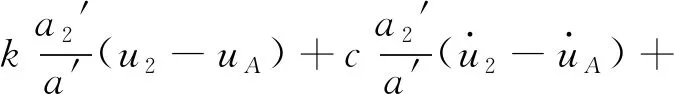
(8)

(9)

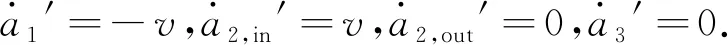
用改進的DSD單元模擬輪胎，建立汽車有限元模型，如圖5所示，進一步建立式(1)所示的振動方程組. 該方程組求解時，由于車輪經過伸縮縫時a2′段脫空，u2是未知量，導致輪底等效位移uB也是未知量. 因此，汽車過伸縮縫時，求方程組(1)的解還要增加a2′段的脫空條件方程，并由迭代方法獲得輪底位移. 迭代方法如圖11所示，增加的方程組為

(10)

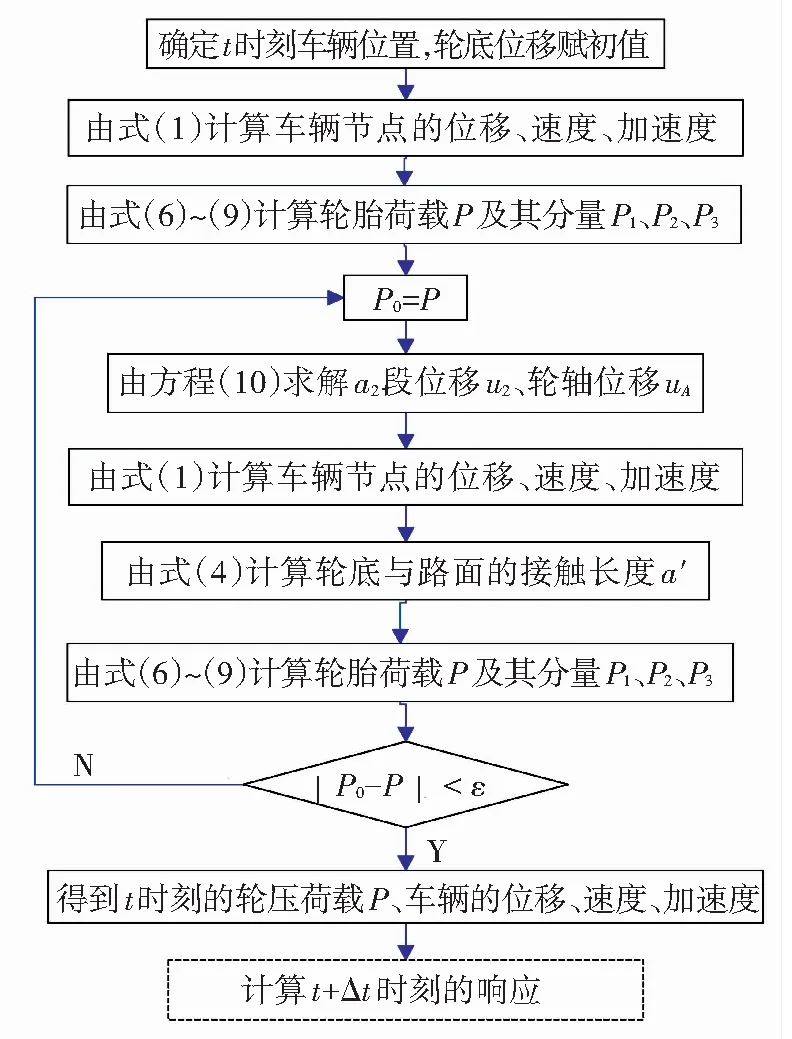
圖11 分析汽車通過伸縮縫的迭代算法

Fig.11 Iteration algorithm in the analysis of vehicle bumping at expansion joint

需要說明的是，本文模型實驗和數值計算研究的都是豎向的輪壓荷載，而不是橫向(順橋向)的輪壓荷載，對順橋向沖擊荷載的研究還有待開展.

3 模型實驗與理論計算結果

3.1 輪胎對伸縮縫的動力荷載

以圖5所示模型車以0.4 m/s的速度通過3 mm縫寬的伸縮縫為例，用第2節方法計算車輪動力荷載. 以前輪為例，結果如圖12所示.

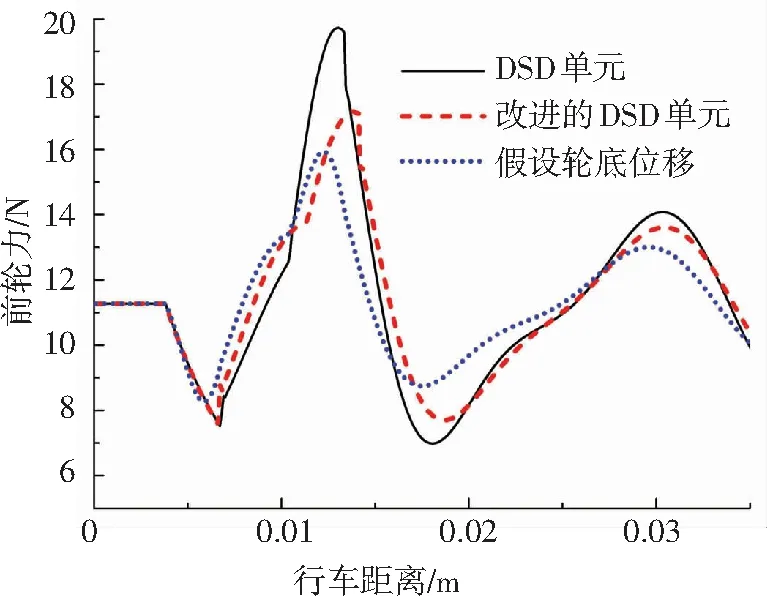
圖12 輪胎對伸縮縫的動荷載

由圖12可知， DSD單元[13]、改進的DSD單元、假設輪底位移這3種算法得到的車輪沖擊荷載變化趨勢一致；DSD單元得到的沖擊力偏大，原因是DSD單元沒有考慮車輪通過伸縮縫時輪底接觸長度的增大，高估了此時輪胎對車體的支撐剛度.

用沖擊系數度量輪胎荷載的動力效應，有

μ=(Pmax-Ps)/Ps.

(11)

其中Pmax為最大動荷載，Ps為靜力荷載. 根據圖4、12和式(11)，計算模型車輪對伸縮縫的荷載沖擊系數. 由DSD單元、改進的DSD單元、假設輪底位移方法得到的前輪荷載沖擊系數分別為0.75、0.52、0.41，而實驗平均值為0.44，由此可知，用改進的DSD單元和假設輪底位移算法得到的沖擊系數更接近實測值.

3.2 輪載沖擊系數的影響因素

以伸縮縫開口寬度、汽車行駛速度作為影響輪胎荷載沖擊系數的主要參數，進一步進行縮尺模型實驗和相應的理論計算.

首先維持模型車的速度不變，為0.4 m/s，測試和計算伸縮縫開口寬度變化時的車輪荷載沖擊系數，所得結果參見圖13. 由此可知：1)輪胎荷載的沖擊系數與伸縮縫的開口寬度近似成正比；2)改進的DSD單元和假設輪底位移方法得到的沖擊系數比DSD單元方法更接近實測值，在伸縮縫開口寬度較大時，以往的DSD單元誤差較大.

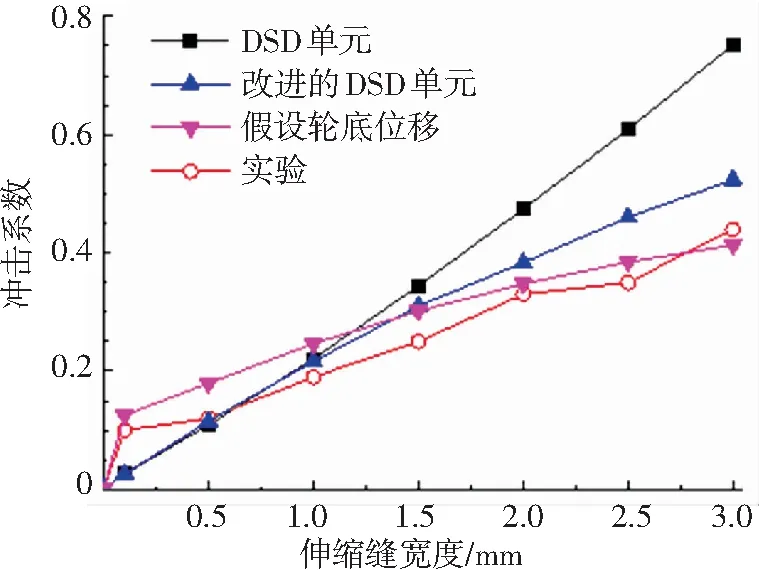
圖13 伸縮縫開口寬度對車輪荷載的影響

Fig.13 Effect of opening width of expansion joint on impact load

如保持伸縮縫寬度為1.5 mm不變，測試和計算不同速度時模型車的跳車沖擊荷載，獲得的沖擊系數如圖14所示，圖14表明：1)當模型車的速度小于0.5 m/s時，輪胎荷載沖擊系數的實驗與計算值都隨著車速的增加而增大；當車速大于0.5 m/s后，沖擊系數計算值不再增加，保持穩定，實測值則繼續增加，但是實驗中發現，當模型車的速度大于0.5 m/s后，車身左右搖晃運行不穩，車橋系統運行振動較大，影響了實驗的可靠性. 2)用改進的DSD單元或假設輪底位移計算方法得到的沖擊系數比以往的DSD單元計算方法所得結果更接近實測值.

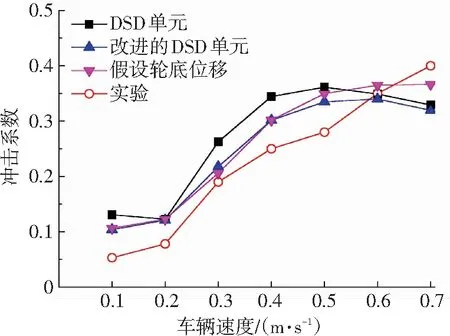
圖14 不同車速下的沖擊系數

對比模型實驗與理論計算的結果，基于改進的DSD單元的計算方法所得結果與實測接近；相比假設輪底位移的計算方法，其假定也較少，因此更適合用于分析車輛輪胎對橋梁伸縮縫的沖擊荷載.

4 載重汽車對伸縮縫的沖擊荷載分析與控制

為了研究實際載重汽車對于橋梁伸縮縫及其周邊橋(路)面的沖擊荷載，本節采用基于改進的DSD單元的方法，對典型的三軸載重汽車對伸縮縫的沖擊荷載進行了計算. 二維的車輛有限元模型如圖15所示，車輛的計算參數見文獻[16]，其所通過的伸縮縫為圖1所示的單縫式伸縮縫.

圖15 典型的三軸載重汽車模型

采用式(11)定義的輪胎荷載沖擊系數來度量載重汽車對伸縮縫的沖擊力. 針對實際橋梁上常見的單縫式伸縮縫，為了涵蓋一般工況下的伸縮縫沖擊荷載，綜合考慮伸縮縫的開口寬度w、載重汽車的速度v的變化，其中開口寬度為1～9 cm，汽車速度為10～80 km/h，求解各種工況(參數組合)下輪胎對伸縮縫的沖擊荷載. 分析結果用車輪荷載沖擊系數的三維云圖來表示，如圖16～18所示.

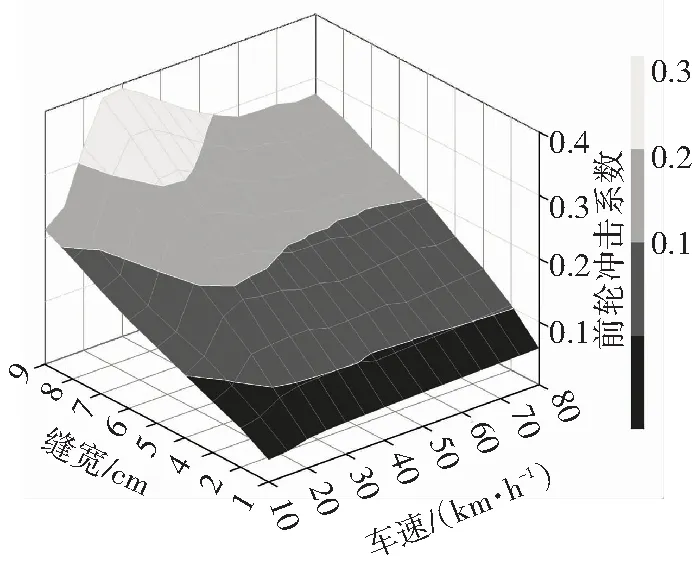
圖16 由改進的DSD單元得到的前輪荷載沖擊系數

Fig.16 Impact factor of front tire obtained by improved DSD element

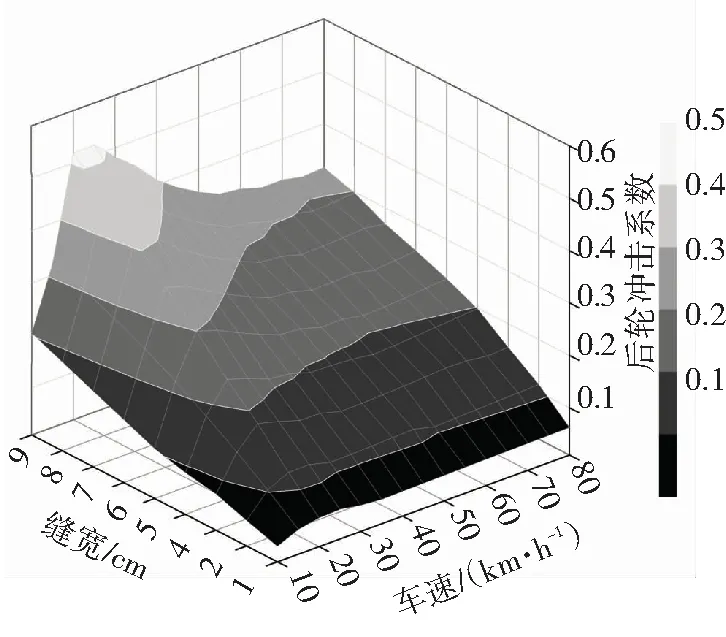
圖17 改進的DSD單元得到的中輪荷載沖擊系數

Fig.17 Impact factor of middle tire obtained by improved DSD element

圖18 改進的DSD單元得到的后輪荷載沖擊系數

Fig.18 Impact factor of rear tire obtained by improved DSD element

由圖16～18匯總得到三軸載重汽車輪胎荷載的最大沖擊系數. 由改進的DSD單元得到的前輪荷載沖擊系數最大值為0.39，該值比中國伸縮縫設計指南[3]的給定值0.45、美國AASHTO規范[4]的給定值0.75小，但是大于中國橋梁規范[17]和歐洲橋梁規范[18]的設計值0.3. 中輪和后輪的沖擊系數仍然小于美國AASHTO規范的給定值，但是大于其他規范或者設計指南的推薦值. 由此可知，當前中國伸縮縫設計指南和橋梁設計規范對伸縮縫跳車輪載沖擊系數的估計略有不足，可能會導致橋梁伸縮縫及其前后橋面的設計強度不足.

由圖16～18還可得到輪載沖擊系數的變化規律：1)在伸縮縫的開口寬度不變情況下，隨著汽車速度的增加，車輪對伸縮縫結構的沖擊力上下波動，最大的沖擊系數在車速為25～30 km/h時出現，因此減小汽車速度不一定能降低車輪對伸縮縫的沖擊力，除非是車輛速度很小時；2)車輪對伸縮縫的荷載沖擊系數與伸縮縫的開口寬度近似成正比例，可以通過減少伸縮縫開口寬度來降低車輪沖擊力. 根據圖16～18，為了控制車輪對伸縮縫的沖擊系數小于中國設計指南的給定值0.45，載重車前輪、中輪、后輪要求的伸縮縫最大開口寬度分別為9.0、7.7、6.4 cm，取三者中的最小值，即要求伸縮縫開口寬度應小于6.4 cm. 因此，該方法也可用來確定保證伸縮縫結構強度安全所容許的開口寬度.

5 結 論

1)設計并制作車輛通過橋梁伸縮縫的縮尺實驗模型，實現了對作用于橋梁伸縮縫上的車輪沖擊力的實測.

2)提出了汽車輪胎對伸縮縫沖擊荷載的兩種改進算法，即假設輪底位移的方法和改進的DSD單元方法，通過與縮尺模型實驗的比較，證明改進算法提高了輪胎沖擊荷載的計算精度.

3)用改進的DSD單元方法，計算了三軸載重汽車的輪胎對橋梁伸縮縫的沖擊荷載，結果表明，最大荷載沖擊系數超過現行伸縮縫結構設計取值.

4)車輪對伸縮縫的荷載沖擊系數與伸縮縫的開口寬度近似成正比，通過減少伸縮縫開口寬度能降低車輪沖擊力，由此可以確定保證伸縮縫結構強度安全所容許的開口寬度.