弱化條件合情推理解決探究問題

熊兵

[摘? 要] 文章通過一個探究問題的分析研究，總結(jié)出探究問題的解決分為兩條主線思路，同時其中一條主線思路分為三種方法，三種方法的核心都是通過弱化條件來解決問題. 應(yīng)用此方法，可以培養(yǎng)學(xué)生的獨(dú)立研究能力、創(chuàng)新能力.

[關(guān)鍵詞] 弱化;合情推理;探究

中學(xué)階段常遇到一些探究問題，中高考也時常將其作為考題. 探究問題類型繁多，如純數(shù)字探究、圖形探究，純數(shù)字和圖形探究又可以分出很多不同的類型. 既然探究問題如此常見，那么值得深入研究.

下面我們來思考這樣一個問題：如圖1，平面內(nèi)五條直線相交于一點(diǎn)，請問有多少對對頂角？對于這樣的題目，方法有很多，本文將深入研究這個題目，進(jìn)而找到比較系統(tǒng)或者常規(guī)的處理方式來解決此探究問題.

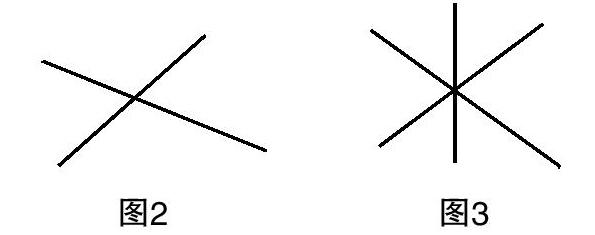
針對這個題目我們來分析一下它的一些做法，第1種方法，可以直接數(shù)，這個方法比較容易出錯，因?yàn)槿菀讛?shù)重或數(shù)漏;第2種方法，這是我們要推廣的一種方法，它適合于這種規(guī)律性的探究問題，同時還可以將其延伸到很多復(fù)雜類型的問題，這種思想就是降低題目的要求，即通過弱化條件來解決問題. 以這個題目為例，本題中5條直線相交于一點(diǎn)，我們注意到5條直線較多，此時降低要求，要有交點(diǎn)，至少需要2條直線（如圖2），容易數(shù)出對頂角的數(shù)量為2對，接下來3條直線的情形（如圖3），4條直線、5條直線. 我們研究從簡單到復(fù)雜的情形，找尋對頂角數(shù)量有什么樣的規(guī)律，由此猜想出平面內(nèi)5條直線相交于一點(diǎn)，對頂角的數(shù)量是多少. 當(dāng)然，這樣數(shù)比較容易出錯，雖然這是一個從簡單到復(fù)雜的過程，但是如果某種情形數(shù)錯，我們就總結(jié)不出正確的規(guī)律. 于是接下來又提供兩種思路，第1種思路，什么樣的情況會產(chǎn)生對頂角，根據(jù)對頂角定義“兩條直線相交會產(chǎn)生對頂角”，那多于兩條直線的情形，我們就任選兩條直線，它都可以形成對頂角，此時我們用排列組合的思想，即相當(dāng)于從n條直線當(dāng)中取兩條直線，產(chǎn)生兩組對頂角. 我們解決了n條直線交于一點(diǎn)的對頂角的數(shù)量（2C■），這是從對頂角定義的角度去思考的. 第1種思路可能不太容易想到，第2種思路是我們在做這類題目時最重要的一種思路. 在第2種思路中，一定要注意研究新加入一條直線之后，對頂角數(shù)量發(fā)生了什么樣的變化. 相同類型甚至很多其他類型的題目都可以用這種思路去研究. 比如兩條直線相交，有兩對對頂角，再加入一條直線，我們就會發(fā)現(xiàn)直接數(shù)會有6組對頂角. 接下來我們的任務(wù)是一定要去研究新增加的這4對對頂角是怎么來的，這樣我們便會研究出再加入一條直線，它又會發(fā)生什么樣的變化，于是我們可以進(jìn)行數(shù)學(xué)歸納，用一個合情推理來解決. 最后我們可以推廣到n條直線在同一平面內(nèi)交于一點(diǎn)有多少對對頂角.

接下來，通過這個題目的研究，我們總結(jié)一下研究過程.

這個模型的構(gòu)建借助于剛才研究的問題，我們對應(yīng)起來解釋，從探究問題出發(fā)，兩種思路，一是直接數(shù)（即直接研究）. 二是弱化條件研究，從兩條直線開始研究，然后又分出三個思路，（1）直接數(shù)，從簡單到復(fù)雜（即直接研究）;（2）研究每一種情況的對頂角數(shù)量，根據(jù)對頂角的定義任選兩條直線都可以形成對頂角，用排列組合的思想，相當(dāng)于從n條直線當(dāng)中取兩條直線產(chǎn)生兩組對頂角，n條直線交于一點(diǎn)的對頂角的數(shù)量就是2C■（即研究問題本質(zhì)）;（3）研究新加入一條直線之后，對頂角數(shù)量發(fā)生了什么樣的變化，合情推理然后得出結(jié)論（即研究問題變化）.

通過此模型，我們來看以下問題.

例1：在△ABC中，畫出一個正方形，要求正方形的一邊在AB邊上，剩下兩個正方形的頂點(diǎn)剛好在AC，BC邊上.

解決方法，弱化條件，畫一個正方形的一邊在AB邊上，剩下一個正方形的頂點(diǎn)剛好在AC邊上，畫出大小不同的情形，然后發(fā)現(xiàn)不同情形的正方形中，剩下的不在三角形邊上的頂點(diǎn)剛好在一條直線上，連接其中不在三角形邊上的任意兩個頂點(diǎn)的直線交BC邊于點(diǎn)D，于是從D點(diǎn)出發(fā)作出正方形即可. （如圖5）

例2：尺規(guī)作圖作已知三角形的外接圓.

解決方法，找到圓心，圓心滿足到三個頂點(diǎn)距離相等，弱化要求，假設(shè)到其中兩個頂點(diǎn)距離相等，則圓心在三角形邊的中垂線上，畫出兩邊的中垂線，交于一點(diǎn)D，即為圓心. （如圖6）

例3：給定兩條平行線及平行線間一點(diǎn)，尺規(guī)作圖作一個圓與給定的兩直線相切并通過已知點(diǎn).

解決方法，此問題同樣需要找到圓心，直徑即平行線之間的距離，既然知道了直徑，因此我們?nèi)趸瘲l件，圓心與已知點(diǎn)的距離確定，可以畫出到已知點(diǎn)距離為半徑的軌跡為一個圓，圓上的點(diǎn)作圓心都可以，再確定圓心在給定的平行線之間的一條直線上，找交點(diǎn)確定圓心.

例4：凸多邊形的對角線條數(shù)問題.

解決方法，我們可以采取兩種不同的弱化方式，一是從四邊形開始數(shù)多邊形的對角線條數(shù)，然后逐漸增加邊數(shù)研究規(guī)律，這種方式剛好符合剛開始舉例的問題，也可以采取三種方法去解決問題;二是弱化到數(shù)一個頂點(diǎn)出發(fā)的對角線條數(shù)，然后結(jié)合所有頂點(diǎn)一起考慮.

例5：多項(xiàng)式（a+b）2020的展示開式的研究.

解決方法，我們可以從指數(shù)為1開始研究，然后指數(shù)為2、指數(shù)為3，展開后研究系數(shù)及字母指數(shù)的變化，得出結(jié)論，同時還可以進(jìn)行推廣研究.

總之，弱化條件合情推理解決問題是一種行之有效且常用的方法，它不但可以解決一些常見的探究性問題，同時還可以推廣出更多有趣、有意義的延伸結(jié)論，甚至有時還能觸類旁通解決不同類型的問題. 應(yīng)用此方法，可以培養(yǎng)學(xué)生獨(dú)立研究能力、創(chuàng)新能力. 有了獨(dú)立研究的經(jīng)驗(yàn)體會，學(xué)生在今后的學(xué)習(xí)過程中將受益匪淺.