由點位與數值之爭引發的思考

付瑜

[摘要]對于小數點變化引起數值大小變化來說，無論小數數字如何展現，客觀上講，小數點移動數值必然就改變了。數字位置的變化和數值變化，這一切都歸因于小數點的移動。這種深刻的認識正是教學所需。教學應該利用這一點來引導學生將視線轉移到小數點的移動上，最終厘清二者之間的因果關系。

[關鍵詞]研讀;編者;意圖;問題;實踐;探索

[中圖分類號]G623.5??[文獻標識碼]A??[文章編號]1007-9068（2020）02-0036-02

北師大版教材編排了研究小數點位移與數值大小變化間的關系的課時——“小數點搬遷”，先觀察小數點的位置變化，再聯系對應數值變化。這個思路是非常新穎的，教學應用價值更為豐富。

一、教材梳理帶來的啟發

1.縱觀蘇教版、人教版和北師大版三個版本的教材，很容易發現，多數教材對這部分內容都極為重視。一方面，小數點移動可以為學生進一步學習小數之間的乘除法提供工具;另一方面，放在宏觀視野里，這個內容與度量單位轉化息息相關，而度量單位之間的進率換算是難點。這種教程編排，為單位換算的教學建立了框架。

2.引發了一些疑問。問題一：人教版教材舍棄此內容，是否暗示其地位的低微？問題二：較之人教版教材，北師大版教材的編排構思反其道而行之，到底孰優孰劣？帶著這兩個疑惑，筆者親身試水，想一探乾坤。

筆者以北師大版教材為樣本，對任教的四（3）班全體學生進行學情摸排。前測問題：（1）從0.01元到0.10元，小數點有何改變？數值有什么改變？（意圖：考查學生的獨立認知。這里是小數點向右移動，數值擴大）（2）從0.01元到0.10元，小數（）（填“擴大”或“縮小”）了（）倍，如何驗證你的結論？（意圖：考查排除掉小數點的位移后，學生對小數大小變化的感知）測試方式：問卷法，兩個問題分開提問。前測問題（1）有33名學生作答，前測問題（2）有37名學生作答。測試結果如下：

前測問題（1）：

[思考]六成多的學生對小數點移動沒有形成有效認知。但是撇開經驗，學生的直覺很準，有近七成的學生能準確判斷數值擴大了10倍。

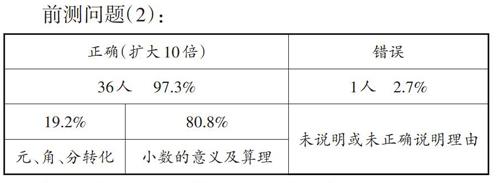
前測問題（2）：

[思考]摒除了小數點，正確率提高到97.3%，這說明學生能準確識別兩個數的倍數關系。多數學生理由充足，都是從小數意義的角度來解釋，沒有人主動想到用小數點來解釋。這是否說明，教學小數乘除法時，真的可以憑直覺經驗和感知力進行，完全棄用“小數點移動”的知識呢？另外，北師大版教材是否能夠很好地揭示出小數點位移帶來數值變化的邏輯關聯呢？

二、帶著問題進行實踐摸索

以小數的乘法為例，研究“有無小數點移動”對教學的影響。為達到研究目的，筆者進行對照實驗。實驗內容：北師大版教材第八冊第三單元“小數乘法”課程。實驗對象：北京市某小學四年級8個班。實驗方法：其中6個班學習原版北師大教材，另外2個班（試驗班）學習刪減“小數點搬遷”后的教材。實驗結果：教學時，2個試驗班（76人），有3名學生對于類似“從4.52到452，擴大了幾倍”存在理解障礙;講解時，筆者結合計數單位和小數意義來揭示其奧妙，學生可以接受;非試驗班在學習了“小數點搬遷”后也存在類似問題;單元學習完后，對8個班進行同等測試，各班的成績相當，即使涉及有關“小數點移動”的專項題目，試驗班的成績也并不差。這表明，人教版教材摒除這部分內容，對涉及單元的學習沒有造成不良影響。

在教學中，以北師大版教材為樣板，研究學生的學習表現。

1.先關注小數點的位移，然后探究小數數值變化，按照這個思路設計教學。根據北師大版教材的編撰思想，先通過情境圖激起學生注意小數點的位移，然后繼續聯想、猜測和探究小數點位移與小數數值變化的關系，進而總結出規律。

教學設計思路：

環節一：呈現情境圖，組織學生觀察從0.01元到0.10元再到1.00元過程中，錢數的改變。（目的：刻意剔除小數點位移帶來的影響，只著眼于兩個數之間的倍率變化）環節二：引導學生自發研究小數點位移后，數值大小的變化趨勢。環節三：拓展規律。（舉例驗證規律的正確性）環節四：練習鞏固。

采用同一套教學設計，筆者對3個教學班進行實驗。環節一中，大部分學生留意到數字“1”的位置改變，極少數學生看到小數點的位置在改變。這有其必然性，因為數字“1”的位置變化很明顯，而小數點的相對位置固定，所以每當此時筆者強行要求學生關注小數點，但均遭到抵觸，造成的后果就是，教師仿佛變得獨裁，學生受到壓制。怎么做才能還給學生自由民主的空間呢？

2.讓數字位移和小數點位移捆綁在一起，溝通關系，以學定教。教師只有將教材諳熟于胸，教學才能輕松自如。筆者對之前的困惑進行了反思：教材對數據的呈現是否欠妥？是改編教材，還是尋求方法上的突破呢？

三、改進后的教學設計

教學設計思路：

環節一：呈現情境圖，引導學生觀察從0.01元到0.10元再到1.00元的變化（目的：讓學生自主審視問題，引出數值的變化和點位的變化）。環節二：點名讓學生暢所欲言，并作全班匯報交流（在此，初步勾連起二者聯系）。環節三：引導自主探究點位向左移動，相應的數值變化。環節四：拓展規律，歸結出兩個變化的邏輯關系（打通聯系）。環節五：練習鞏固，加深認識。

改進后的方案只在一個班實驗。學生的反應非常fi然，教師也很順心。教師不再強勢，學生變得更加積極活躍，這樣的教學才是真正的以學定教。

四、教學實驗后的反思

教學的訣要不在于“教”，為學生服務，打造適合學生接受的教案才是根本。如果一個課程里蘊含著深厚的數學原理，就應努力挖掘，挖得越深，教學就越有底氣。把握數學本質，會使教師站位更高。例如，學習“小數的意義”時，教師補充完善了十進制的內容，但是只是孤立靜止地看待十進制——相鄰數位的計數單位存在10倍關系。當引導學生從小數點的位移切入觀察數值變化時，同一數字因為位置不同而導致代表的數值不同，這樣的變化更有規律可循，所用的仍是十進制，這樣學生就會更加靈活地掌握十進制。運算很多時候就是以數的意義為依托的，學生對數的意義理解越深刻，計算就越自信。

教學要謹防經驗主義作祟，多方位審查問題，會使教師對教材把握得更充分、更客觀。教師不要執迷于自己的感覺，也不要輕易被同行的言論左右，必須全面了解，研讀教材、研究學生，積極進行實踐探索，才能取得教學的真經。