一種具有寬松約束的相位—高度映射算法

王景隆，曹益平，李城夢，付光凱，萬瑩瑩，王亞品，王 璐

(四川大學 電子信息學院，成都 610064)

光學式三維測量具有高精度測量、非接觸性、無損測量等優點，已被廣泛用于逆向工程、生物與醫學工程、工業檢測、質量控制等領域[1-5].其中相位測量輪廓術(PMP)[6-7]具有點對點相位計算及全場分析等優點，更倍受業界青睞.在PMP系統中，帶有相移量的正弦條紋由投影裝置將其逐一投射到被測物體表面，由成像裝置逐一對應采集被物體表面調制的變形相移條紋，最后由數據處理裝置對采集的數據進行處理，得到物體表面的相位分布[8].要得到被測物體的真實高度，就要建立相位到高度的映射關系.相位—高度映射關系的待定系數，可由成像裝置光心與投影裝置光心之間的距離，參考面與投影裝置光心之間的距離以及兩裝置光軸之間的夾角等系統結構參數確定，這種需要測量系統結構參數的高度校準方法為顯式校準[9-10]，但在實際測量中很難精確測量這些參數值.通常通過建立相位-高度映射關系，由已知平面高度與測得的對應相位來標定映射關系中的待定系數，這種高度校準方法為隱式校準[11-13]，避免了直接測量系統結構參數困難的問題.

傳統的相位—高度映射算法要求成像裝置光軸與投影裝置光軸共面且交于參考面內的一點，成像裝置光軸平行于參考平面的法線，參考面平行于兩裝置光心的連線，但在測量中要全部滿足這些條件是很苛刻的，在搭建系統時很難精確實現.為此，業界學者對搭建的測量系統結構進行了改進，并提出了相應的相位—高度映射算法.文獻[14]介紹了相位—高度的映射關系，并且證明了當投影裝置光軸和成像裝置光軸不共面時，傳統的相位—高度的映射關系也是適用的，但仍然要求參考面必須平行于投影裝置光心與成像裝置光心的連線.文獻[15]提出既不用保證參考面平行于投影裝置光心與成像裝置光心的連線，也不要求成像裝置光軸垂直參考面，但兩光軸必須共面且交于參考面一點的相位—高度映射關系.本文在傳統的相位—高度映射算法的基礎上，提出一種新的具有寬松約束的相位—高度映射算法.這種算法不要求投影光心和成像光心的連線平行于參考平面，也不要求投影光軸與成像光軸共面且交于參考面一點，只要保證成像裝置光軸垂直于參考平面，即可實現相位到高度的映射.通過數學模型推導發現所提相位—高度映射中的待定系數不僅與系統的結構參數有關，也與參考平面的相位分布有關.

1 PMP測量原理

投影裝置將帶有相移量的正弦條紋投影到被測物體表面，其光強I(x,y)為[16]

I(x,y)=R(x,y)[A(x,y)+B(x,y)cos(φ(x,y)+δ)].

(1)

式中：R(x,y)為物體表面不均勻的反射率，A(x,y)為背景光強，B(x,y)為條紋對比度，φ(x,y)為受物體高度調制的相位分布，δ為條紋每次的相移量.對于N(N≥3)步相移法，光強In(x,y)為

(2)

式中n為N步相移法的步數，由式(2)計算可得相位φ(x,y)為

此時相位φ(x,y)被截斷在反正切函數的主值范圍(-π,π]內，因而是不連續的，需要進行相位展開將其恢復成原有的相位分布，連續相位分布記為φ(x,y).要由物體的相位分布得到物體的三維形貌，需要建立相位—高度的映射關系.

2 寬松約束的相位—高度映射算法

傳統相位—高度映射算法和所提相位—高度映射算法的測量光路如圖1(a)、(b)所示：

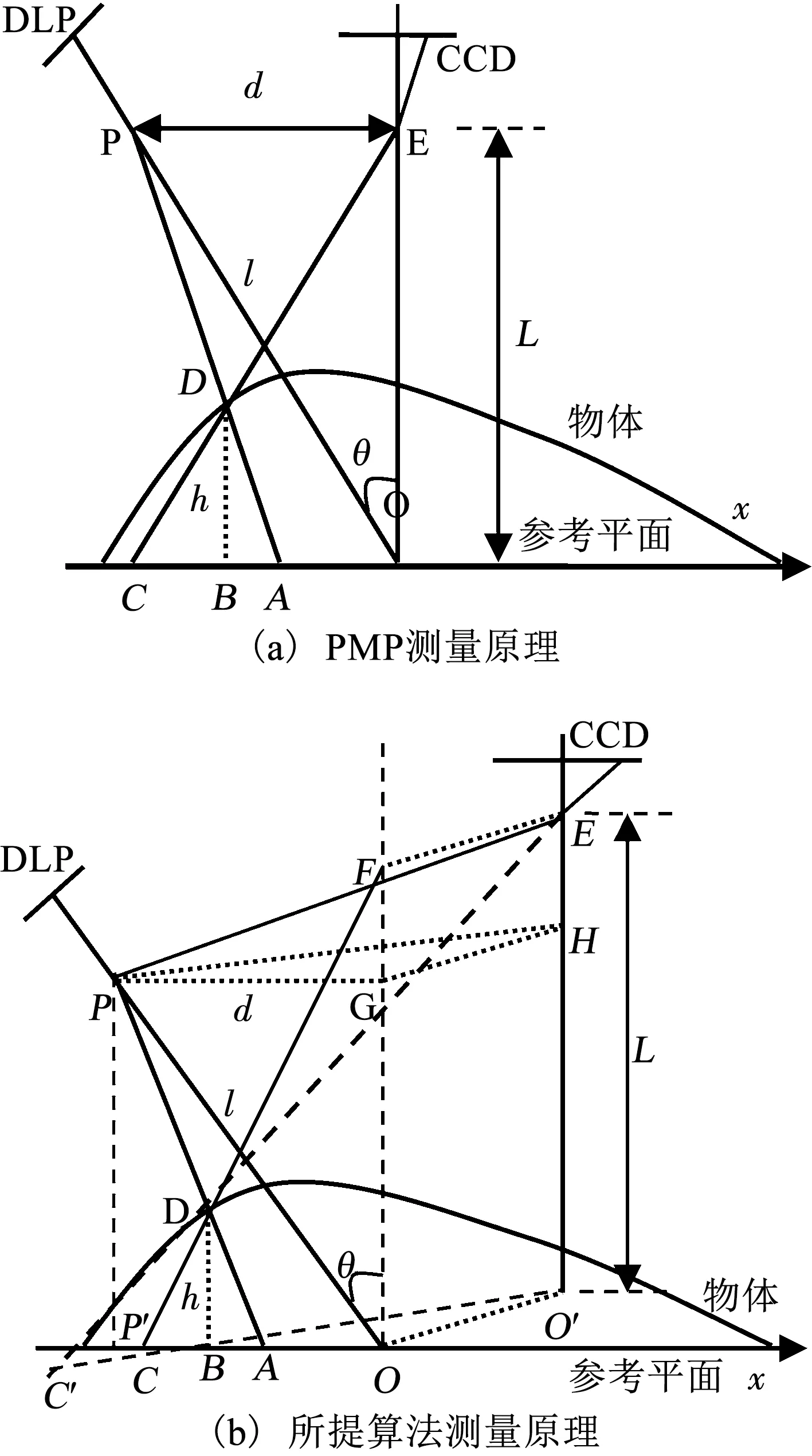
圖1 測量原理

在圖1(a)中，DLP為數字投影裝置，CCD為成像裝置，P是DLP的光心，E是CCD的光心，PO是投影裝置的光軸，EO是CCD的光軸并垂直于參考面，PO和EO相交于參考平面上的O點，D是物體上的任一點.l是投影裝置光心到參考平面上O點的距離、d是兩裝置光心之間的距離、L是CCD光心與參考面之間的距離、θ是投影裝置光軸和CCD光軸之間的夾角，它們都是系統的結構參數.從圖1(a)分析可知，要求投影裝置的光心和CCD的光心連線與參考平面平行，并且要求兩光軸共面并交于參考面一點.

圖1(b)中的P點、E點、A點、B點、D點、l以及L和圖1(a)中相同.DLP的光軸PO與參考面相交于O點，CCD的光軸EO′垂直于參考面并交于O′點，EF平行于OO′，平面PGH平行于參考面，交FO于G點，交EO′于H點.P點到G點之間的距離為d，DLP的光軸PO與FO之間的夾角為θ.由于DLP和CCD的光心和光軸都是不可見的，因此在實驗中很難保證DLP與DLP光心的連線恰好平行于參考面，也難以保證兩裝置的光軸共面且恰好相交于參考平面上一點.而在圖1(b)中，不再要求兩裝置的光心連線平行于參考平面，也不再要求兩光軸共面且交于參考面上一點，只需保證CCD的光軸垂直于參考平面，以便于建立圖像坐標與世界坐標的簡單映射.因而圖1(b)所示測量光路約束更寬松，更易于搭建.

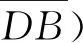
(3)

式中φ為D點的相位，考慮到CCD探測器的陣列特性，式(3)可被寫為

文獻[14]提出當系統結構一定時，a1(x,y)和b1(x,y)應該是恒定不變的，可由標定獲得.后來，文獻[13]提出要考慮鏡頭畸變的影響，式(3)被修正為

(4)

式(4)在PMP系統中經常用于系統標定，以下簡稱為Li′s算法.

從圖1(b)可看出，兩裝置的光心連線PE與參考平面不平行, 且PO與EO′不共面，推導物體表面任一點D點的高度h的過程如下：

當采用遠心光路的PMP系統時，在參考平面上看到的投影正弦光柵是等周期分布的，其周期為p0，在參考平面上的相位分布φ(x)是坐標x的線性函數[17]，記為

當PMP系統是發散光路時，正弦光柵被投影到參考平面上，φ(x)是x的非線性函數，但是參考平面上每一點相對于參考點O的相位值是唯一的且單調變化的.此時參考平面上條紋周期的分布為[18]

(5)

從式(5)可看出，參考平面上的條紋周期p(x)與x成非線性的關系，各點的周期分布隨點的變化而改變.這種非線性給各點的相位計算帶來了不便.因此，在計算參考面上各點的相位值時，將其映射到周期p0上.同樣，在計算物體上各點的相位時，也將其映射到周期p0上，測得的物體上各點相位與對應點在參考平面上的相位差，即反映了物體高度的相位信息.因此，可得圖1(b)中參考平面上A，B，C點的相位φ:

(6)

由于D點被投射到參考平面A點處，A點與D點具有相同的相位，即

(7)

由三角形BCD和OCF相似可得出

(8)

再由三角形BDA和PPA′相似可得出

(9)

(10)

(11)

式(10)即可寫為

(12)

式中：φC為參考平面的相位分布，φCD為物體上各點的連續相位與參考平面上對應點相位的差值.

當兩裝置的光心連線平行于參考平面且O與O′重合時，圖1(b)與圖1(a)相同，此時從圖1(a)中可知lcosθ=L，由式(11)可知，b22=0，即式(12)可化為式(3).表明圖1(a)所示測量光路是圖1(b)所示測量光路的一個特例.

從式(12)可知，所提出的相位—高度的映射算法不僅與系統的結構參數有關，還與參考面上的相位分布有關.所提算法對應的系統結構，不要求投影裝置光心和成像裝置光心的連線平行于參考平面，也不要求投影光軸與成像光軸共面，使得系統的搭建更加容易.所以為了得到物體的真實高度，實現相位到高度的映射，所提算法相比傳統的算法更具優勢.當考慮CCD探測器的陣列特性，可將式(12)表達為

(13)

式(13)φC(x,y)為參考平面的相位，可事先通過測量參考平面得到并存于計算機.因此，在標定a2(x,y)、b21(x,y)和b22(x,y)時，則需要測量4個或者4個以上已知高度的平面(包括參考平面)，以求出所測平面的連續相位，將平面的高度和對應的相位代入式(13)中，求得對應的a2(x,y)、b21(x,y)和b22(x,y)即完成標定.

3 實驗及分析

搭建的實驗裝置如圖2所示，其中使用的數字光投影儀型號為PLED-W200 DLP，成像系統CCD型號為MVC1 000MF.測量前利用型號為Zolix TSA300-B的電動平移臺帶動一個標準平面沿z軸移動并結合CCD圖像，反復調整CCD，直至CCD光軸垂直標準平面.

圖2 實驗裝置

通過計算機產生周期為20像素的768×1 024大小的正弦光柵圖，采用5步相移技術.使用標準平面相對于參考面沿z軸移動預設高度的方法進行參數標定.考慮到CCD各像元之間的靈敏度差異性和隨機誤差的影響，a1(x,y)，b1(x,y)和c1(x,y)應該呈現具有一定波動厚度的特征分布.在大量的系統標定實驗結果中選取兩組不同結構參數下b1(x,y)的分布圖如圖3所示.圖3(a)為結構參數1(Structural Parameters 1,SP1)下的實驗結果，圖3(b)結構參數2(Structural Parameters 2,SP2)下的實驗結果.

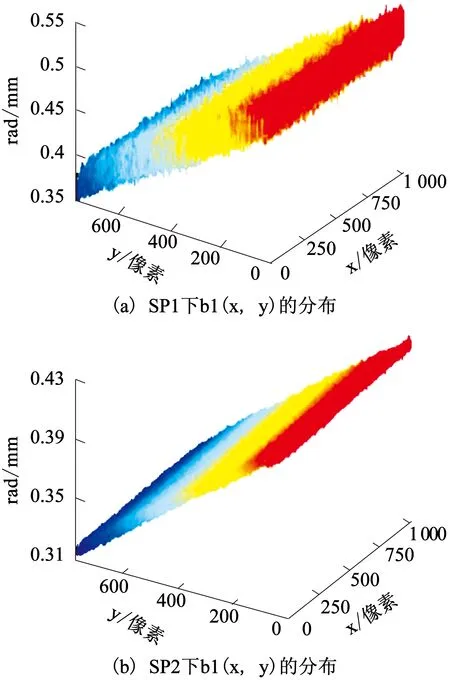
圖3 b1(x,y)分布

從圖3可看出，在不同結構參數下，b1(x,y)具有不同的波動厚度且呈現不同的傾斜角度特征.在式(13)中1/φ(x,y)的系數可寫為b21(x,y)+b22(x,y)φC(x,y)，為了比較兩者的區別，通過大量的實驗，發現b21(x,y)+b22(x,y)φC(x,y)是呈有一定波動厚度且有一定傾角的斜平面的特征分布.兩組代表性的不同結構參數下的實驗結果如圖4所示，圖4(a)～(b)為結構參數3(Structural Parameters 3,SP3)下的實驗結果，圖4(c)～(d)為改變DLP和CCD的位置后重新測量的結果，即結構參數4(Structural Parameters 4,SP4)下的一組實驗結果.

圖4(a)為SP3下b1(x,y)的分布，b1(x,y)是一個具有一定傾角的斜面且具有一定波動厚度，正如上圖3中所示.圖4(b)為SP3下b21(x,y)+b22(x,y)φC(x,y)的分布，也是一個具有一定傾角且有一定波動厚度的斜平面.由圖4(a)和圖4(b)可知，二者的傾斜角大致相同，但是后者的斜面波動厚度明顯小于前者且表面更光滑.由于波動厚度是由測量誤差等因素引入的，波動厚度越小則表征測量精度越高.由此可知，運用1/φ(x,y)的系數為b21(x,y)+b22(x,y)φC(x,y)的式(13)進行相位到高度的映射，重建效果更好，精度更高.

為了證明上述實驗的可重復性，對測量系統的結構參數進行了多次改變，即隨意改變投影裝置和成像裝置的位置，然后進行測量.圖4(c)、(d)為代表SP4下的一組實驗數據.結果同樣表明，圖4(d)和圖4(c)的傾斜角基本相同，但仍然是后者的斜平面的波動厚度明顯小于前者.

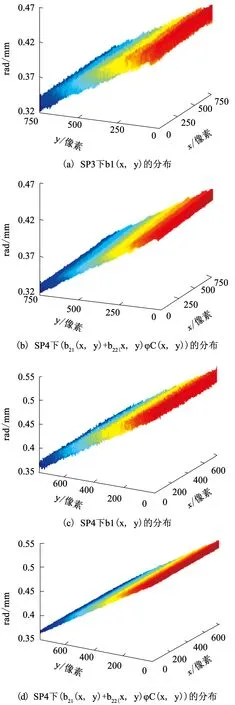
圖4 兩組不同結構參數(SP3和SP4)下驗證b1(x,y)與b21(x,y)+b22(x,y)φC(x,y)的關聯性的實驗結果

Fig.4 Experimental results of the correlation betweenb1(x,y) andb21(x,y)+b22(x,y)φC(x,y) under two groups of structure parameters SP3 and SP4

通過對上述實驗結果的分析可知：在相同的結構參數下，利用所提算法式(13)進行標定得到的b21(x,y)+b22(x,y)φC(x,y)的分布，其斜面波動厚度要明顯小于利用式(4)標定得到的b1(x,y)的分布的波動厚度.正如上文所說波動厚度是由測量誤差等因素引入的，波動厚度越小表征測量精度越高.因此，可表明所提算法在測量精度上要優于傳統的算法，且所搭建的測量系統結構也更易于實現.

為了驗證所提測量方法的精確性，測量3 mm到24 mm等若干已知高度平面的相位分布，并分別通過式(4)和式(13)進行相位高度映射.得到平均絕對誤差(MAE)和均方根誤差(RMS)的對比結果如圖5所示.表1中列出其中3 mm、8 mm、16 mm 3個測量結果，包括平面真實高度h0，由兩種算法恢復出平面的平均高度havg，平均絕對誤差(MAE)和均方根誤差(RMS).

表1 對已知高度平面測量復結果對比

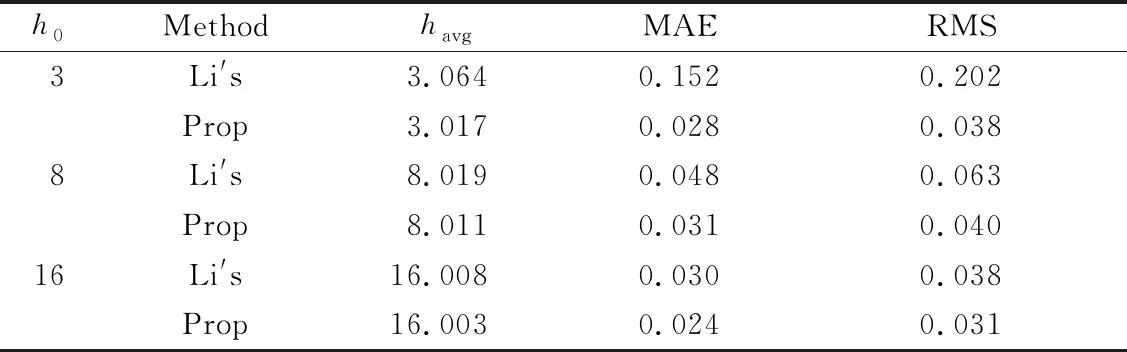
Tab.1 Comparison of measuring results of the planes with known heights mm

圖5 各平面的平均絕對誤差(MAE)和均方根誤差(RMS)對比

從表1和圖5可看出，所提算法所恢復平面的平均高度都比Li′s算法更接近平面的真實高度，同時平面的平均絕對誤差和均方根誤差也均小于Li′s算法.在高度平面較低的區域，Li′s算法恢復平面的精度較低，隨著測量平面高度的增加，Li′s算法所恢復平面的精度逐步提高并在測量高度大于10 mm的平面時，其精度逐漸趨于穩定，但仍低于所提算法的精度.而所提算法一直保持了較好的測量精度，較之更加穩定.因此可得，所提的相位—高度映射算法的準確性和可重復性都要優于Li′s相位—高度映射算法.

為了驗證該方法的實用性，對如圖6(a)中所示的“心”形物體進行了三維形貌的測量.圖6(b)為由CCD采集所得的一幀物體變形條紋，圖6(c)為根據采集所得物體變形條紋中得到的物體截斷相位的信息分布.圖8為分別采用Li′s算法和所提算法來實現相位到高度的映射對比效果.圖8(a)為所測“心”形物體的連續相位信息分布，圖8(b)為Li′s算法重構出的三維物體形貌.圖8(c)為所提算法重構出的三維物體形貌.

圖6 “心”形物體測量數據

為了驗證該方法在不同特征環境下的可重復性，對如圖7(a)中所示的“米奇”形物體進行了三維形貌的測量.圖7(b)為由CCD采集所得的一幀物體變形條紋，圖7(c)為根據采集所得物體變形條紋中得到的物體截斷相位的信息分布.圖9為分別采用Li′s算法和所提算法來實現相位到高度的映射對比效果.圖9(a)為所測“米奇”形物體的連續相位信息分布，圖9(b)為Li′s算法重構出的三維物體形貌.圖9(c)為所提算法重構出的三維物體形貌.

圖7 “米奇”形物體測量數據

圖8 “心”形物體相位到高度的重構結果

由圖8(b)可看出，Li′s算法雖然恢復出了物體的三維形貌，但是在一些局部區域出現了毛刺，使得在這些點上相位到高度的映射呈現難以對應的關系，并且在圖8(b)中所重構出的物體表面出現了一定失真.而由圖8(c)可看出，所提算法很好地恢復了物體面形，整體沒有出現毛刺現象，而且表面輪廓也比較光滑，使測量的精度得到了保證，有效實現了相位到高度的一一映射.對于高度更高的“米奇”形物體，由圖9(b)可看出，Li′s算法所重構出物體的三維面形存在一定程度的失真，而由圖9(c)可看出，所提算法所重構的面形區域則更加光滑，尤其是在面形頂部區域.并且所提算法的測量精度也較Li′s算法的高，綜上可得，所提出相位—高度映射算法在實現相位到高度的映射效果上要優于Li′s算法.

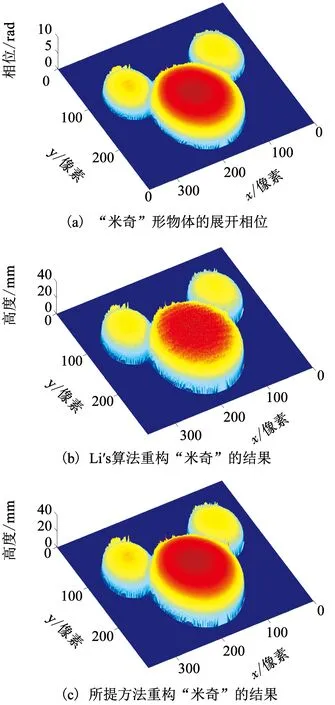
圖9 “米奇”形物體相位到高度的重構結果

4 結 論

本文從實驗系統的實際光路出發，考慮到實際光路難以精確達到理想模型要求，提出了一種新的具有寬松約束的相位—高度映射算法.這種算法既不需要滿足成像裝置光軸與投影裝置光軸共面且交于參考面內的一點，參考面平行于兩裝置光心的連線的要求，也不需要滿足兩光軸必須共面且交于參考面一點的要求.只要求成像裝置光軸垂直于參考平面，即可實現相位到高度的映射.理論分析和實驗驗證發現，當投影裝置光心與成像裝置光心的連線不平行于參考平面時，相位—高度映射不只與系統的結構參數有關，還與參考平面的相位分布有關.完成了對比測量實驗，在對高度分別為3 mm、8 mm和16 mm的平面測量中，使用傳統算法進行的相位—高度映射時，其平均絕對誤差和均方根誤差最大可達0.152 mm和0.202 mm.而使用所提算法進行的相位—高度映射時，其平均絕對誤差和均方根誤差最大不超過0.031 mm和0.040 mm，有效驗證了所提算法的準確性和可重復性.通過 “心”形物體的面形測量驗證了所提算法的實用性.