四元數矩陣重構魯棒波束形成算法

張 雪,朱向鵬,劉 帥,閆鋒剛,王 軍

(1.哈爾濱工業大學(威海) 信息科學與工程學院,山東 威海 264209； 2.中國空間技術研究院西安分院,西安 710000)

極化敏感陣列的自適應波束形成技術能夠同時利用極化信息和空域信息完成濾波，相比傳統標量陣列的純空域濾波具有更加優良的抗干擾能力，使其在重要的軍事、民事等領域具有廣泛的應用前景[1-2].四元數具有4個正交基，特別適用于極化敏感陣列的信號建模及信號處理，因此其在極化敏感陣列上得到了廣泛的應用[3-4].文獻[5]提出的四元數MVDR(Quaternion Minimum Variance Distortionless Response, Q-MVDR)算法在干擾噪聲協方差矩陣(interference-plus-noise covariance matrix, IPNCM)及期望信號導向矢量精確已知時具備優越的性能.然而，在實際應用中，許多非理想因素不可忽視.如：由指向誤差、陣元位置誤差帶來的期望信號導向矢量失配[6-8]；精確的IPNCM難以獲得，利用采樣協方差矩陣代替，在期望信號較強時，會出現信號相消現象，引起算法性能急劇下降[9-10].因此，對基于四元數的魯棒自適應波束形成算法(Robust Adaptive Beamforming, RAB)進行研究十分必要.

在RAB算法方面，文獻[11-12]利用對角加載(Diagonal Loading, DL)技術改善了對導向矢量誤差的敏感性，但是并沒有準則來確定最優加載量.針對此問題，文獻[13-14]提出的迭代RAB算法、基于收縮失配估計的RAB算法避免了加載量的求解，并提高了在導向矢量失配時算法的魯棒性.但是，以上RAB算法都有一個共同的缺點：由于訓練數據中包含期望信號成分，當期望信號較強時，算法性能下降.因此，文獻[15]利用Capon空間功率譜估計器對與期望信號分離的區域進行積分重構得到了IPNCM，去除訓練數據中的期望信號成分，在波束形成領域實現了有價值的創新，為RAB技術的發展提供了一種新思路.但是該算法忽略了干擾信號的功率，并且需要利用CVX工具包求解二次約束二次規劃問題，不易實現.在該算法的基礎上，文獻[16-18]提出的改進算法利用斜投影、去除殘余噪聲等方法在一定程度上提高了重構IPNCM的精度，以及導向矢量失配時的魯棒性，但在這兩方面仍具有一定的改進空間.

綜上，在標量陣列、強期望信號條件下，矩陣重構類方法極大地提升了波束形成算法的魯棒性.但是在極化敏感陣列方面，已有研究成果尚未有效解決強期望信號和導向矢量失配情況下性能下降的問題.本文針對此問題，提出一種基于四元數矩陣重構的魯棒波束形成算法，該算法利用四元數完成信號建模，將協方差矩陣重構方法擴展到四元數域，結合四元數信號子空間投影方法，完成了對極化敏感陣列最優權矢量的求解.仿真實驗表明，在強期望信號和導向矢量失配時，本文算法表現出較好的魯棒性.

1 四元數信號模型

1.1 四元數基礎

將復數在四維空間上進行擴展，可以得到四元數，比較常用的是Hamilton四元數.其定義四元數q由4個分量組成，一個實部和3個虛部[19]，可以表示成如下形式

q=a+ib+jc+kd.

式中i,j,k都是虛部單位，滿足

i2=j2=k2=ijk=-1, ij=k, ji=-k,

ki=j, ik=-j, ik=i, kj=-i,

四元數具有如下性質：

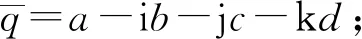
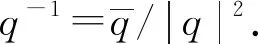
一個四元數q可以表示成2個復數q1，q2相加的形式如:q=q1+iq2，其中q1=a+jc，q2=b+jd，且q1，q2唯一.

1.2 四元數信號模型

為了簡化闡述，文中假設接收極化波為完全極化波，陣列工作在理想環境下.

極化敏感陣列由相互正交的M個電偶極子對構成，陣列結構如圖1所示，整個陣列可以分為2個子陣，分別由沿x軸和y軸方向放置的電偶極子組成，接收來自x軸和y軸方向的電場分量.各個陣元沿y軸構成均勻線陣，陣元間距為d.

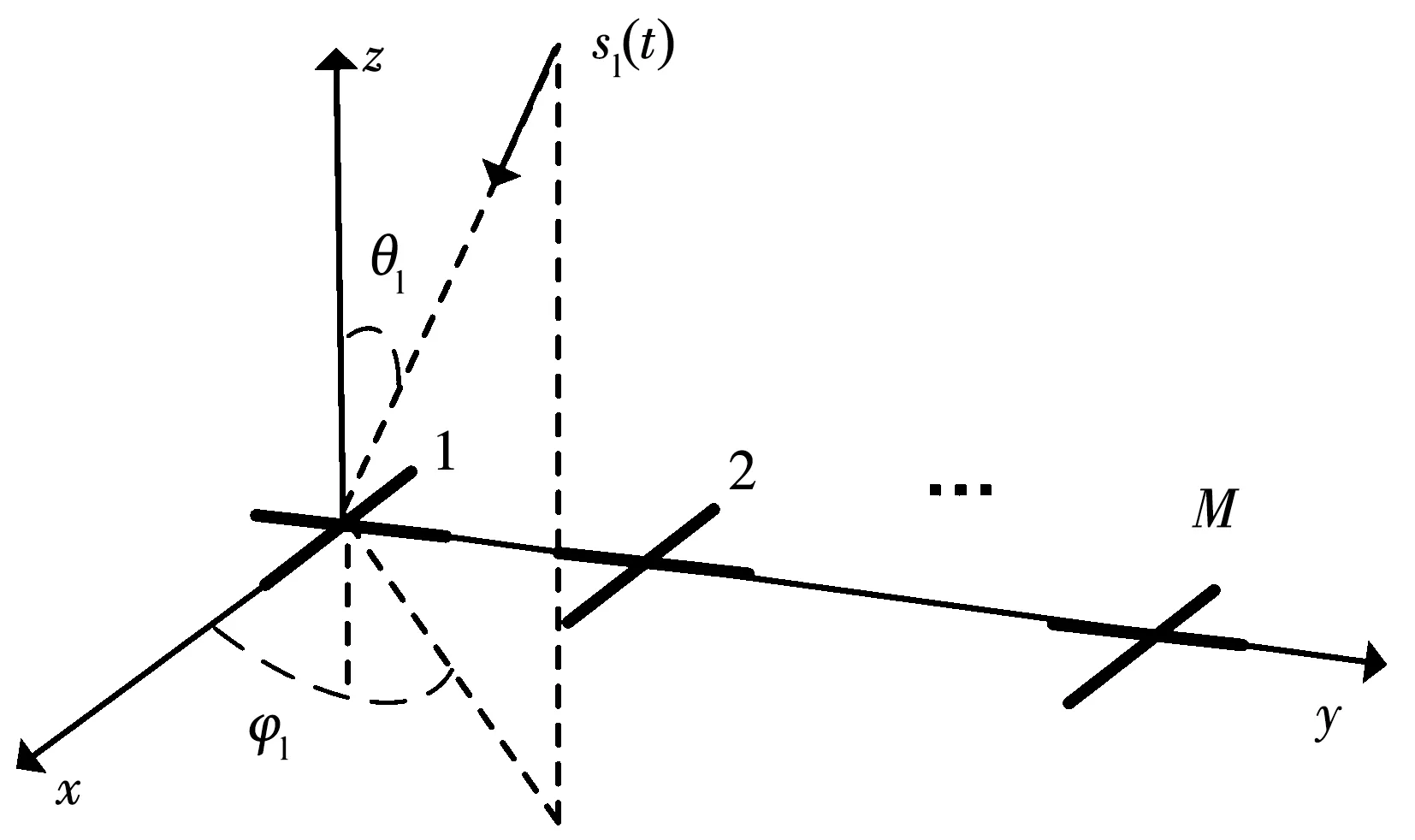
圖1 交叉偶極子均勻線陣

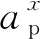
根據偶極子方向，可將陣列分為垂直、水平偶極子兩個子陣，這兩個子陣上第l個信號的導向矢量可表示為

則兩個子陣的輸出x1(t)和x2(t)分別為

式中：n1(t)和n2(t)分別為兩個子陣中與信號相統計獨立的高斯白噪聲矢量.

四元數具有4個正交基，極化敏感陣列的每個陣元有兩個正交分量，整個陣列的輸出可以表示成四元數的形式，保持了各分量之間固有的正交特性.四元數域極化敏感陣列的輸出可表示為

x(t)=x1(t)+ix2(t)=

(1)

式中：a(θl,γl)?ax,l+iay,l為第l個信號的四元數域導向矢量，n(t)?n1(t)+in2(t)為四元數域噪聲矢量.

在波束形成中，式(1)一般表示為

式中：a0為期望信號導向矢量，s0(t)為期望信號，al,(l=1,2,…L)為干擾信號導向矢量，sl(t),(l=1,2,…,L)為干擾信號.

四元數域的協方差矩陣R∈HM×M為

干擾噪聲協方差矩陣Rj+n定義為

(2)

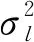
1.3 Q-MVDR波束形成算法

Q-MVDR算法的最優權矢量w∈HM×1可以依據最大輸出信干噪比(max signal-to-interference-plus-noise ratio, MSINR)準則轉化為如下問題求得

(3)

利用拉格朗日乘子法求解式(3)，解得四元數域最優權矢量的表達式為

(4)

(5)

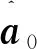
2 基于四元數矩陣重構的魯棒波束形成算法

2.1 干擾噪聲協方差矩陣重構

針對強期望信號時，MVDR算法出現性能下降并且會加重導向矢量失配的問題，文獻[15]提出復數域標量陣列的重構IPNCM的方法，本文將其擴展到四元數域

(6)

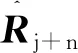
(7)

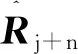
第l個干擾信號的導向矢量位于Bs各列矢量bi張成的干擾子空間，即可用Bs各列線性表示

式中：?αB∈RP×1為系數向量，R為實數集.

(8)

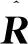
第l個干擾信號的導向矢量也可以用Es線性表示

式中?αE∈R(L+1)×1為系數向量.

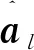
aL+1=PBPEaL.

當L趨近于∞時，aL收斂于真實的導向矢量，即：a∞=PBPEa∞.根據文獻[20]，a∞的求解問題可以等價為對矩陣PBPE中特征值為1的特征向量的求解問題，有

式中eigmax( )代表矩陣的最大特征值.矩陣PBPE的最大特征值為1.

得到

(9)

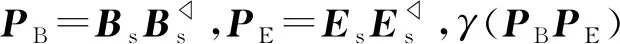
最后，利用Capon譜估計器得到第l個干擾信號的功率

(10)

(11)

(12)

2.2 四元數信號子空間投影

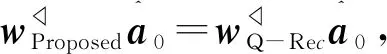
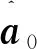
得到最優權矢量

(13)

綜上，本文提出的基于四元數矩陣重構的魯棒波束形成算法，具體步驟如下

步驟3：根據干擾信號個數，利用式(9)和(10)得到干擾信號的導向矢量和功率的估計值；

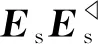
3 算法性能分析

定義四元數波束形成器信干噪比損失[20]為

(14)

將式(4)代入式(14)得到最優波束形成器的信干噪比損失為

最優波束形成器的輸出SINR可以表示為

(15)

在強期望信號和導向矢量失配情況下，算法性能嚴重下降的原因有以下兩種情況：

1)訓練數據中不含期望信號時導向矢量失配的權矢量為

(16)

將式(16)代入Sout，得到

(17)

則信干噪比損失為

結合式(15)得

Smis=SCBFLoptLmis.

可見，此時由導向矢量失配引起的信干噪比損失與期望信號強度無關，當失配角較小時，Lmis接近為1.

2)訓練數據中含有期望信號時導向矢量失配，信干噪比損失為

(18)

并且有

Smis+sp=SmisLsp=SCBFLoptLmisLsp.

由式(18)可知，此時的信干噪比損失與期望信號強度有關，期望信號越強，信干噪比損失越大，甚至會出現強期望信號時的輸出SINR比弱期望信號時還要低的現象，這就是強期望信號引起性能下降的原因所在.此外，導向矢量失配對算法性能的影響比不含期望信號時大[21].

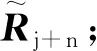
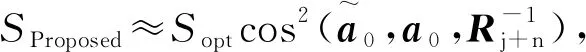
SProposed≈SoptLProposed≈Sopt.

因此，本文算法的輸出SINR接近于最優值.

4 仿真分析

仿真條件：由8個偶極子構成的均勻線陣，陣元數M=8，陣元間距d=λ/2，采樣快拍數K=200，期望信號參數為(θ0,γ0)=(0°,10°)，導向矢量失配誤差為2°，S=10 dB，干擾信號參數為(θ1,γ1)=(50°,20°)，I=30 dB.

在以上仿真條件下，將本文算法(Proposed)與四元數域PCMR-Q-MVDR算法[17]、CCMR-Q-MVDR算法[15]、對角加載(DL-Q-MVDR)算法[11]、Q-MVDR算法[5]和最優(Optimal)算法進行對比分析，考察算法方向圖、輸出信干噪比等方面的性能.

4.1 強期望信號時不同算法方向圖比較

本實驗考察強期望信號情況下，不同算法的方向圖對比，仿真結果如圖2所示.

圖2 強期望信號時方向圖的對比

Fig.2 Comparison of beampatterns in strong desired signal case

由圖2可知，DL-Q-MVDR和Q-MVDR算法出現期望信號相消的現象，即：期望信號方向產生了零陷；CCMR-Q-MVDR算法在期望信號方向出現較小的估計偏差；本文算法和PCMR-Q-MVDR算法都精確對準期望信號并具有較低的旁瓣.

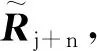
4.2 輸出信干噪比隨輸入信噪比的變化

本實驗在導向矢量失配條件下，考察不同算法輸出SINR隨輸入SNR的變化情況.仿真條件改變S=-10 dB～20 dB，進行500次蒙特卡洛獨立實驗，仿真結果如圖4所示.

圖3 強期望信號時干擾零陷深度的對比

Fig.3 Comparison of interference depth in strong desired signal case

圖4 輸出SINR與輸入SNR的變化曲線

由圖4可知，Q-MVDR算法在SNR很小時，性能已經出現下降；DL-Q-MVDR算法雖然一定程度上改善了算法的性能，但是當SNR>0 dB時，算法性能也明顯下降；本文算法、PCMR-Q-MVDR和CCMR-Q-MVDR算法由于重構出IPNCM，輸出SINR隨著輸入SNR線性增加.本文算法相比其他兩種重構類算法，具有更高的輸出SINR，并接近于最優值.

4.3 輸出信干噪比與失配角度的關系

本實驗在強期望信號條件下，對不同算法輸出SINR與失配角度的關系進行仿真.仿真條件改變失配角度為-10°～10°，進行500次蒙特卡洛獨立實驗，仿真結果如圖5所示.

由圖5可知，Q-MVDR算法即使很小的失配角度，就會引起性能嚴重惡化；DL-Q-MVDR算法一定程度上提高了對失配角度的敏感性，但當失配角度大于2°時，算法性能嚴重下降；CCMR-Q-MVDR算法進一步提高了對失配角度的敏感性，但當失配角度大于5°時，性能也出現明顯下降；本文算法和PCMR-Q-MVDR算法都對失配角度不敏感，但本文算法具有更高的輸出SINR，當失配角度較大時，依舊較接近于最優值.

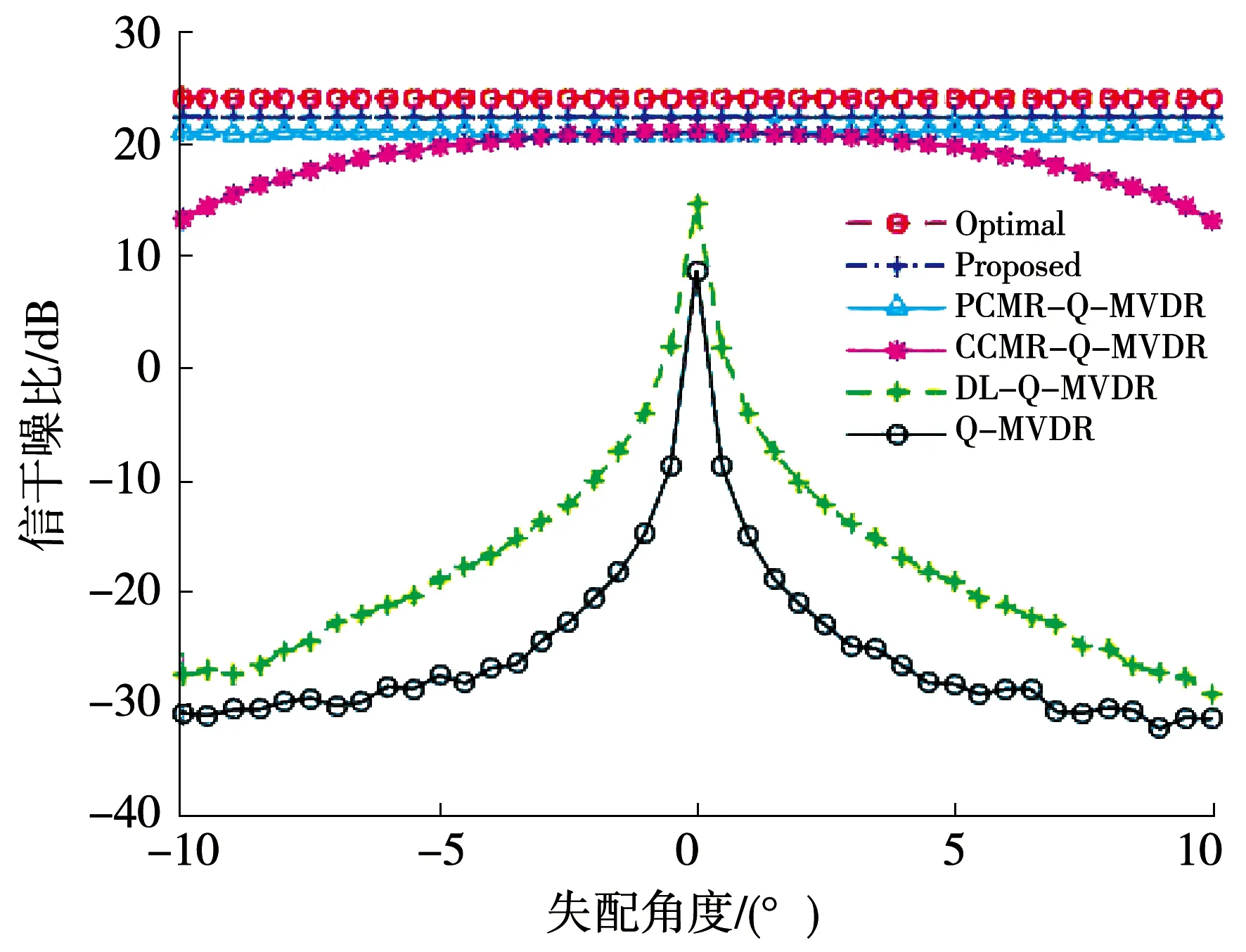
圖5 期望信號失配時輸出SINR與失配角度關系

Fig.5 Correlation between output SINR and mismatch angle in the case of desired signal steering vector mismatch

5 結 論

針對在強期望信號和導向矢量失配的情況下，Q-MVDR算法性能下降的問題，提出了一種基于四元數矩陣重構的魯棒波束形成算法.該算法首先利用四元數矩陣重構方法得到IPNCM的精確估計；然后利用四元數特征空間投影對導向矢量失配誤差進行修正.仿真結果表明，本文算法在強期望信號和導向矢量失配同時存在時，能夠保證期望信號方向波束增益無損失的同時，實現對干擾的有效抑制；算法始終具有較高的輸出SINR，有效地提高了算法的魯棒性.