淺談利用極限思想分析函數圖像

鄭鵬

【摘?要】極限思想不僅僅局限于大學數學分析等高等數學中的應用，在高中的函數及其圖像問題中，也起到了很重要的作用。

【關鍵詞】極限思想;函數圖像;趨近于;變化趨勢

“極限”是數學中的分支——微積分的基本概念，廣義的“極限”是指：某一個函數中的某一個變量，此變量在變大（或者變小）的永遠變化過程中，逐漸向某一個確定的數值A不斷地逼近而“永遠不能夠重合到A”的過程中，此變量的變化，被人為規定為“永遠靠近而不停止”、其有一個“不斷地極為靠近A點的趨勢”。極限是一種“變化狀態”的描述。此變量永遠趨近的指A就叫做“極限值”。這是百度百科對“極限”一詞的描述。極限的英文名叫“limit”，在數學中的符號就是“lim”，主要應用于微積分。

而所謂極限思想，其實就是用極限的概念分析問題和解決問題的一種數學思想。這是微積分的基本思想，在大學數學分析這門課中，如函數連續性、導數以及定積分等等都是借助于極限來定義的。

用極限思想解決問題的一般步驟就是：對于被考察的未知量，先設法正確地構思一個與它的變化有關的另外一個變量，確認此變量通過無限變化過程的“影響”趨勢性結果就是非常精密的約等于所求的未知量;用極限原理就可以計算得到被考察的未知量的結果。與一切科學的思想方法一樣，極限思想也是社會實踐的大腦抽象思維的產物。極限思想可以追溯到古代，例如，劉徽“割圓術”就是建立在直觀圖形研究基礎上的一種原始可靠的“不斷靠近”的極限思想的應用。

那么在數學史中占據如此重要地位的極限思想，是否僅用于大學數學分析等高等數學中的研究呢？它在我們高中數學教學中又有哪些重要的應用，就是我想闡述的本篇文章中我個人對極限思想在高中數學中的應用，尤其是在函數及其圖像中的應用。

在高中數學的函數內容學習中，函數單調性是函數最重要的一個性質，等同于一個函數的靈魂，有了單調性，我們就把握住了一個函數的命脈，知道了它的走向。我們利用導數來分析函數單調性，有了單調遞增和單調遞減，或者恒等于某個值，這些都是我們可以通過函數的導數得到的。但是知道了一個函數單調性，我們離畫出一個函數圖像還存在一個難點，就是從哪開始，又到哪結束。這就好比于我們知道了一個函數走向，可是從哪走到哪我們并不清楚，畫出的圖像也是存在問題的。

用一個最簡單的我們最熟悉的函數來看：反比例函數，我們通過求導發現，導數，是恒小于零的，意味著是一直單調遞減的，那我們是否在定義域上就畫出一條遞減的曲線呢？那我們在畫出它的圖像中，還存在一個難點，就是從哪遞減到哪，這也就是很多學生困惑的地方。雖說大家都對反比例函數圖像很了解，但是為什么長這樣，大部分同學還是停留在初中對它利用描點法畫出的圖像上。那么我們的極限思想，在這就對函數圖像有一些新見解。我們發現，當值無限趨近于時，值仍然是正數，且接近于0;當值無限趨近于0但仍然為正數時，值就會趨近于。而在區間上，導數又是一直小于零的，所以我們能分析出來，這個函數在上單調遞減，而且是從開始一直遞減到接近0的，且一直為正數。

同樣道理，在上，當值無限趨近于時，等于將會變成一個無限靠近0的負數;當值無限趨近于0且為負數時，值就會趨于。所以這個函數在上也是單調遞減，而且是從接近0的負數開始一直遞減到的，且一直為負數。

那么如此我們針對的圖像就有了大概的形狀，當然，這只是對一個簡單函數的應用，極限思想的厲害之處不僅于此，我們來看一下下面一些題型，感受下極限思想的重要之處。

例1：函數的大致圖像是（?）

這種函數圖像的問題是高考熱點題型，對于這個函數，我們發現它并沒有奇偶性，求導分析又過于復雜，也沒有任何一個特殊值的位置，那么分析起來就存在一定的難度，這時候我們可以借助極限思想來分析函數，當值從右邊無限趨近于0時，即無限趨近于0且為正數時，分子為正數，也為正數，則為正數。所以排除選項。當無限趨近于時，分子為正數，也為正數，但是指數函數相對于二次函數來說增長性是最強的，（當無限趨近于時，函數增長性：指數函數>三次函數>二次函數>一次函數>對數函數），所以分母相對于分子來說特別地大，則函數值將會無限趨于0且為正數，則能選出正確選項。

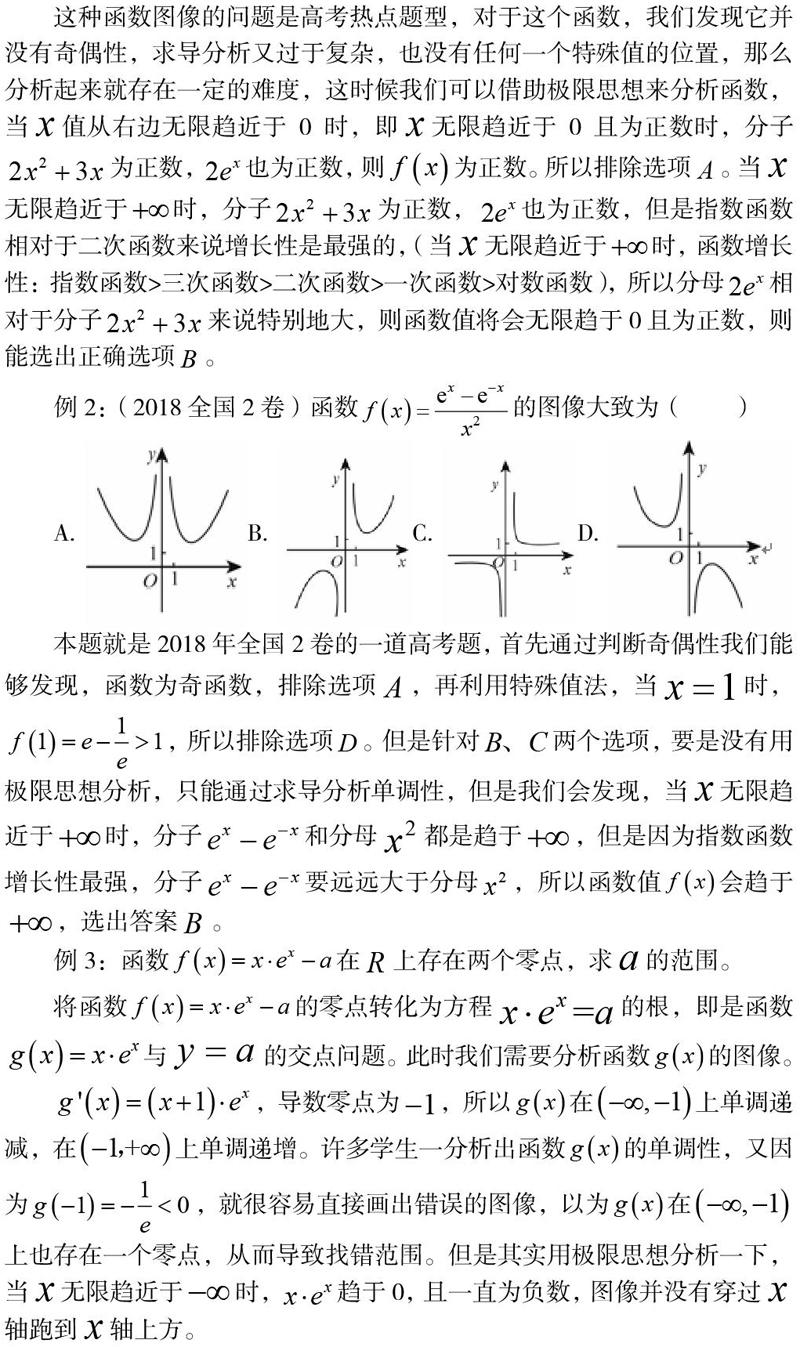
例2：（2018全國2卷）函數的圖像大致為（）

本題就是2018年全國2卷的一道高考題，首先通過判斷奇偶性我們能夠發現，函數為奇函數，排除選項，再利用特殊值法，當時，，所以排除選項。但是針對兩個選項，要是沒有用極限思想分析，只能通過求導分析單調性，但是我們會發現，當無限趨近于時，分子和分母都是趨于，但是因為指數函數增長性最強，分子要遠遠大于分母，所以函數值會趨于，選出答案。

例3：函數在上存在兩個零點，求的范圍。

將函數的零點轉化為方程的根，即是函數與的交點問題。此時我們需要分析函數的圖像。

，導數零點為，所以在上單調遞減，在上單調遞增。許多學生一分析出函數的單調性，又因為，就很容易直接畫出錯誤的圖像，以為在上也存在一個零點，從而導致找錯范圍。但是其實用極限思想分析一下，當無限趨近于時，趨于0，且一直為負數，圖像并沒有穿過軸跑到軸上方。

以上三道例題，充分體現了極限思想在函數的學習過程中起到了至關重要的作用。某些高考熱門題型，利用極限思想就能夠迅速得到答案。然而現在許多學生都只是停留在通過求導分析函數單調性的地步，某些基礎好一些的同學可能能夠根據某些點處的函數值大概確定函數圖像，但是并不知道在無窮遠這些沒有邊界的地方，函數是怎樣變化的。所以我覺得在高中的數學教學中，將極限思想滲透到學生分析函數過程的固有思維中，能夠加強學生對函數這一大塊重難點的突破。

參考文獻：

[1]李芳.極限思想的產生與發展[J].語數外學習（高中版中旬），2020（05）：64-66.

[2]梅永健.淺談高中數學中的極限思想[J].語數外學習（高中版上旬），2017（06）：43.

[3]謝慧杰.極限思想的產生、發展與完善[J].數學學習與研究（教研版），2008（09）：27.

（作者單位：云南衡水呈貢實驗中學）