“認識垂直”教學設計

馬倫

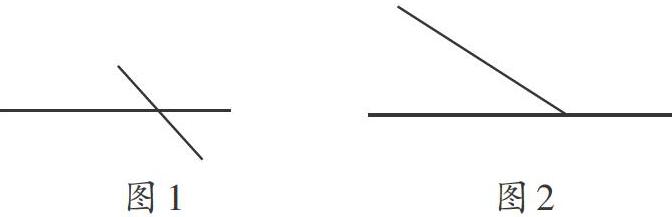
[摘 要]認識垂直是空間與圖形領域的內容，是學習幾何圖形特征的基礎。根據學科特點和學生的認知規律，運用數形結合的思想、經歷概念形成過程、從角的維度來進行教學，有利于加深學生對垂直概念的理解，發展學生的空間觀念。

[關鍵詞]垂直;操作;教學; 設計

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2020）35-0073-02

【教學內容】新人教版教材第七冊第57頁～58頁

【教學目標】

1.通過動手操作感受平面上兩條直線互相垂直的關系，認識垂線、垂足。

2.通過自主操作和合作交流，學會用合適的方法畫一組垂線，能借助直尺、三角板等工具畫垂線。

3.通過感知、操作、觀察、應用等活動培養學習空間與圖形知識的興趣，發展空間觀念。

【教具準備】課件、方格紙、小棒、直尺、量角器、正方形彩紙、水彩筆

【課前思考】

垂直是空間與圖形領域的內容，是學習幾何圖形特征的基礎。學生對垂直的深度理解一直是教學難點，通過分析學生的易錯題，發現學生畫的垂線與已知直線夾角不是90度的原因不是學生的動手能力不好，沒有完全理解相交與垂直的概念才是主要原因。于是本課改變原有教學設計：先簡單揭示相交與垂直的概念，然后教畫垂線的方法，學生嘗試畫垂線……這是根據學生已有的知識經驗和認知規律，運用數形結合的思想從“量”的角度進行教學設計。

【教學過程】

一、從角的維度，提出問題

師：上節課我們已經學習了有關平行的知識，今天就來研究兩條直線相交的情況。

師（出示圖1、2）：哪一組直線是相交的？

生1：圖1的兩條直線相交的，因為它們有交點。

生2：圖2兩條直線也是相交的，因為直線是無限延伸的，所以它們肯定是相交的。

師：不錯，圖1和圖2都是相交的。

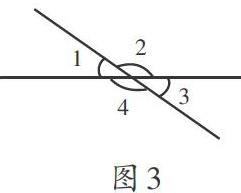
師：兩條直線相交組（如圖3）成了幾個角？哪些角是相等的？

生3：角1和角3是相等的，角2和角4是相等的，因為它們是對頂角。

師：角1加角2等于多少度呢？角3加角4等于多少度呢？

生4：都等于180度，因為它們拼成了1個平角。

師：兩條直線相交，什么情況下，角1=角2=角3=角4？

生5：90度，因為角1+角2+角3+角4拼成了1個周角。

師：你能試著用準備好的材料把相交的這種特殊情況表示出來嗎？

【設計意圖：從角的維度研究相交不僅符合知識的建構規律，也符合學生已有的認知基礎。學生通過對“角的度量”單元的學習已經有相交的知識經驗。垂直是相交的特殊情況，兩條直線相交就會形成4個夾角，提出“四個角中哪些是相等”的問題，能調動學生利用已有經驗解決問題的學習積極性，為接下來研究兩條直線相互垂直做好鋪墊。】

二、動手操作，體驗垂直

師：請利用準備好的材料和工具進行小組合作，表示相交這種特殊情況。

（出示：方格紙、量角器、鉛筆、正方形彩紙、直尺）

折：匯報不同的折法，重點強調為什么折痕相交成90度。

畫：用三角板、量角器、直尺上的刻度、方格紙上的線等畫出的垂線。

擺：用鉛筆擺一擺，重點強調擺的時候要注意什么。

師：用什么方法能夠驗證表示的垂直對不對？

生1：用三角尺的直角來比對。

師：當兩條直線相交成直角時，我們就說這兩條直線互相垂直，其中一條直線是另一條直線的垂線。（出示概念）

師：如果一條直線稱作是a，另一條直線稱作是b，我們可以怎么說？

生2：直線a與直線b互相垂直，直線a是直線b的垂線，直線b也是直線a的垂線。

師（用手遮去其中一條直線）：這是垂線嗎？（強調互相垂直）互相是什么意思？

師：兩條直線相交成直角還有一個交點呢，我們稱它為垂足。

師：現在你理解什么是互相垂直了嗎？它與相交是什么關系？

（學生回答略）

師：找一找，生活中互相垂直的例子比比皆是，看看能找到多少互相垂直的例子，記得說清楚誰與誰互相垂直。

【設計意圖：概念教學過程中，需要讓學生經歷概念形成的過程。如果直接告知兩條直線相交成90度，兩條直線相互垂直，學生對其僅是停留在記憶層面，沒有理解垂直的本質。本設計僅僅圍繞一個核心問題（什么時候四個角都是直角），通過動手操作，先建構垂直的表象，然后歸納得出垂直的概念。這樣既豐富了學生對垂直概念的認識，也發展了學生的空間觀念和動手操作能力。】

三、自主探究，過一點畫已知直線的垂線

師：這有一條直線，要過一點A畫這條已知直線的垂線，先想一想A點可以在哪里？你可以自己選擇把A點畫在直線上還是直線外。如果有困難可以看看書。

（指名板演，討論畫法）

師：A點畫在直線上還是直線外，畫法有什么相同之處呢？都是借助什么工具？

師：第一步都是用三角板的一條直角邊與已知直線重合，另一條直角邊與A點重合，最后沿著這條直角邊過A點畫一條直線，標上直角符號表示兩條直線互相垂直。這條直線就是已知直線過A點的垂線。還有什么不同的畫法？

師：怎樣檢驗畫的是否正確（用直角板檢驗），同桌互相檢查。

師：用學會的畫法做另外三題。

師：做完這三題，有什么要提醒大家的？（直線不是水平方向的，三角尺要隨著直線移動）

師：無論用什么方法，我們畫的垂線都要與已知直線相交成直角。

【設計意圖：經過一點畫已知直線的垂線，是學生理解了兩條直線相互垂直概念后的運用，也是本節課的教學難點。通過設計練習，讓學生在練習中經歷了自主嘗試——交流——檢驗——總結的過程，降低學生學習的難度。】

四、介紹數學運用，體會數學價值

師（介紹魯班發明角尺及角尺的現實運用）：垂直在日常生活中有著廣泛的應用，希望你有一雙充滿靈性的眼睛去發現數學中的生活和生活中的數學。

五、全課小結

師：通過這節課的學習，你有什么收獲？

【教后思考】

幾何概念是研究一切空間與圖形的基礎。小學生的認知水平基本處于“具體運算階段”，認識幾何圖形主要是通過動手操作，進而積累這些圖形的經驗，獲得感知。基于本節課的教學實踐，我對幾何概念教學策略有下面三個方面的認識。

1.創設情境，要基于學生的已有知識經驗

好的問題情境是一種能激起學生情感體驗的心理場，是學習數學的“引爆器”，它能激發學生在思考、探索中完成數學知識的學習。以學生的已有知識經驗創設情境，不僅能充分調動學生的積極性，還能為學生學習新知識做好鋪墊。學生在學習“角的度量”之前對相交是有認知基礎的，創設一個判斷相交的情境，就充分溝通了新舊知識之間的聯系，激起學生情感體驗的心理場，凸顯學生的學習主體性。

2.概念認知，要讓學生經歷概念的形成過程

概念的形成過程指：概念引入的必要性及對感性材料的認識、分析、抽象和概括。經歷概念形成的過程有利于促進學生對概念的整體理解。本節課先通過引導學生猜想四個夾角是90度的兩條直線的位置和形狀，再通過畫、折、擺等活動幫助學生建立垂直的表象，最后揭示垂直的概念。如果采取機械重復、死記硬背概念的教學方法，不讓學生經歷概念的形成過程，學生就很難從多個維度獲得對概念個性化的認知。

3.突破難點，恰當運用數形結合思想

一節好課必須要在突破難點上下功夫，才能起到“牽一發而動全身”的效果。本節課的教學難點就是畫垂線，很多學生畫的兩條直線相交的夾角不是90度。于是，在形成概念前先讓學生猜想兩條直線相交，什么時候4個夾角才相等，并運用準備好的學具動手操作，教師再揭示垂直的概念。在學生自主畫垂線階段，注重檢驗：從角的維度分析是不是垂直的。這樣，學生自然就知道：如果夾角不是90度，那么這兩條直線就不互相垂直。通過數據之間的關系來認識圖形的形，其實就是運用了數形結合的數學思想。

[ 參 考 文 獻 ]

[1] 張奠宙，孔凡哲等.小學數學研究[M].北京：高等教育出版社，2009.

[2] 吳正憲.小學數學課堂教學策略[M].北京：北京師范大學出版社，2015.

[3] 李斌.創設數學教學情境，實施有效課堂教學[J].數學學習與講究（教研版），2008（9）.

[4] 施曉玲.重視概念形成過程的教學.天水師范學院學報[J]，1997（3）.

[5] 張曉霞，李建萍.小學數學課程與教學論[M].四川：四川教育出版社，2006.

（責編 童 夏）