巧用補(bǔ)形法研究四面體問(wèn)題

曾睿

[摘? 要] 立體幾何問(wèn)題中，有一類問(wèn)題可以通過(guò)補(bǔ)形法，得到一個(gè)常見(jiàn)的幾何體，使復(fù)雜的線面關(guān)系變得清晰明了. 文章從一道例題出發(fā)分析解決這類問(wèn)題的方法，并在此基礎(chǔ)上總結(jié)規(guī)律，歸納常見(jiàn)的一些四面體的補(bǔ)形方法.

[關(guān)鍵詞] 立體幾何;四面體;補(bǔ)形

教學(xué)中，遇到這樣一個(gè)問(wèn)題：已知在半徑為2的球面上有A，B，C，D 四點(diǎn)，若AB=CD=2，則四面體ABCD的體積最大值為多少？

這是某年數(shù)學(xué)全國(guó)卷的第12題，主要考查幾何體的體積的計(jì)算、球的性質(zhì)、異面直線間的距離，通過(guò)球這個(gè)載體考查學(xué)生的空間想象能力和推理計(jì)算能力.

解答是這樣的：過(guò)CD作平面PCD，使AB垂直于平面PCD，交AB于P. 設(shè)點(diǎn)P到CD的距離為h，則有V■=■×■×2×h×2=■h，當(dāng)直徑通過(guò)AB與CD中點(diǎn)時(shí)，h■=2■=2■，故V■=■.

本小題這個(gè)解答當(dāng)中，學(xué)生比較疑惑的有兩點(diǎn)：（1）為什么可以過(guò)CD作平面PCD，使AB垂直于平面PCD，能這樣作的前提是AB和CD要垂直，那為什么認(rèn)定體積最大時(shí)AB和CD要垂直？（2）為什么直徑通過(guò)AB與CD中點(diǎn)時(shí)，距離h最大？

要解釋清楚這兩個(gè)疑點(diǎn)，首先需要補(bǔ)充說(shuō)明一個(gè)公式.

四面體體積公式：如果一個(gè)四面體的兩條相對(duì)棱的長(zhǎng)分別是a，b，它們的距離為d，所成的角為θ，那么它的體積為V■=■abdsinθ（證明見(jiàn)后）.

根據(jù)這個(gè)公式，我們首先得到結(jié)論：AB和CD必須垂直，即sinθ=90°時(shí)才能得到最大的體積.

其次，由于AB=CD=R（球的半徑），所以連結(jié)球心O和四個(gè)頂點(diǎn)，則容易知道△OAB和△OCD都是正三角形.

設(shè)AB的中點(diǎn)為E，CD的中點(diǎn)為F，則OE⊥AB，OF⊥CD.

設(shè)AB與CD間的距離為d，有d≤EF≤OE+OF. （異面直線間公垂線段最短）

因此，OEF共線時(shí)，四面體的體積可以達(dá)到最大值，因?yàn)镺E=OF=■，故V■=■.

？搖？搖這樣解決一個(gè)選擇題比較花費(fèi)時(shí)間，而且在高中數(shù)學(xué)教學(xué)中，不涉及四面體的體積公式，異面直線的距離即公垂線段的長(zhǎng)度在教學(xué)中也僅僅要求了解.下面我們用補(bǔ)形的思路來(lái)解決這個(gè)問(wèn)題.因?yàn)轭}目當(dāng)中兩條線段長(zhǎng)度一樣，所以考慮把這個(gè)四面體補(bǔ)形成一個(gè)長(zhǎng)方體：

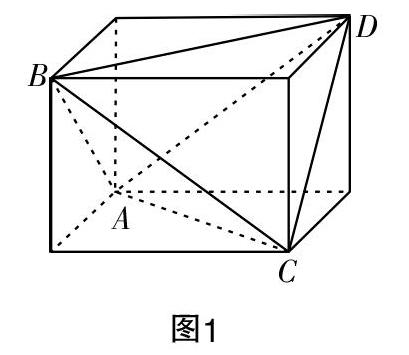
如圖1：

則四面體的外接球即是長(zhǎng)方體的外接球，四面體的體積是長(zhǎng)方體的體積減去四個(gè)全等的小三棱錐的體積.

設(shè)長(zhǎng)方體的邊長(zhǎng)為a，b，c，體對(duì)角線即為外接球的直徑，得到：

a2+b2+c2=42，b2+c2=22，所以a=2■，

則V■=V■-4V■=abc-4×■×■abc=■abc=■.

又b2+c2=22 ，所以V■=■≤■（b2+c2）=■，

當(dāng)且僅當(dāng)b=c=■時(shí)，等號(hào)成立.

從等號(hào)成立的條件可以比較容易地看出是在AB和CD垂直時(shí)，四面體的體積取到了最大值.

我們會(huì)發(fā)現(xiàn)，使用補(bǔ)形，一下子把陌生的幾何體變得熟悉了，原本錯(cuò)綜復(fù)雜的線面關(guān)系也變得清晰起來(lái). 利用這一方法解決某些幾何問(wèn)題，思路清晰明朗，較其他方法簡(jiǎn)潔明了.

比如剛才提到的四面體的體積公式也可以用補(bǔ)形法得到.

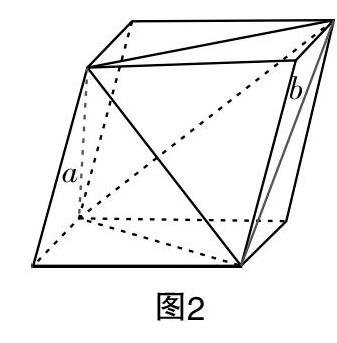
一個(gè)四面體的兩條相對(duì)棱的長(zhǎng)分別是a，b，它們的距離為d，所成的角為θ，將四面體補(bǔ)形成平行六面體（因?yàn)橄鄬?duì)棱的長(zhǎng)度不確定，相等的時(shí)候才能補(bǔ)成長(zhǎng)方體）.

如圖2：

那么該平行六面體的底面積為S=■absinθ，平行六面體的體積為V■=■abdsinθ. 同樣，該平行六面體由原四面體和四個(gè)全等的三棱錐構(gòu)成. 三棱錐與平行六面體的高相等，底面積為平行六面體的一半，V■=■×■×■absinθ=■absinθ.所以V■=V■-4×V■=■absinθ.

一起來(lái)看一下常見(jiàn)的幾種四面體補(bǔ)形方式：

一、把四面體的四個(gè)面各補(bǔ)上一個(gè)三棱錐，最后形成一個(gè)平行六面體. 其中正四面體是最特殊的形式，可以補(bǔ)成正方體. 而對(duì)棱相等的四面體則可以補(bǔ)形成一個(gè)長(zhǎng)方體.

例1：正四面體棱長(zhǎng)為a，求外接球的半徑R.

正四面體補(bǔ)形為一個(gè)正方體，正四面體的外接球即為正方體的外接球.

如圖3：

正方體的面對(duì)角線是正四面體的棱長(zhǎng)，體對(duì)角線為外接球的直徑.

設(shè)正方體邊長(zhǎng)為b，則a=■b，2R=■b，所以R=■a.

例2：在三棱錐A-BCD中，AB=CD=3，AD=BC=4，AC=BD=5，求三棱錐A-BCD外接球的半徑.

因?yàn)橛腥M對(duì)棱相等，把四面體補(bǔ)成一個(gè)長(zhǎng)方形，如圖4：

長(zhǎng)方體的三個(gè)面的面對(duì)角線是三棱錐的棱長(zhǎng)，體對(duì)角線是外接球的直徑.

設(shè)長(zhǎng)方體的棱長(zhǎng)為a，b，c，外接球的半徑為R，

則a2+b2=32，b2+c2=42，a2+c2=52，（2R）2=a2+b2+c2，所以R=■.

二、把四面體的一個(gè)角作為平行六面體的一個(gè)角補(bǔ)形成平行六面體.

例3：四面體ABCD，側(cè)棱AB，AC，AD兩兩垂直，AB=2，AC=3，AD=4，求四面體的外接球的半徑R.

因?yàn)樗拿骟w的側(cè)棱兩兩垂直，所以可以把這個(gè)角看作長(zhǎng)方體的一個(gè)角，把四面體補(bǔ)形成一個(gè)長(zhǎng)方體，則四面體的外接球就是長(zhǎng)方體的外接球

四面體的三條側(cè)棱就是長(zhǎng)方體的長(zhǎng)、寬、高，外接球的直徑就是長(zhǎng)方體的體對(duì)角線，則（2R）2=AB2+AC2+AD2=29，所以R=■.

例4：若三棱錐S-ABC的所有頂點(diǎn)都在球O的球面上，SA⊥平面ABC，SA=2■，AB=1，AC=2，∠BAC=60°，求球O的半徑R.

根據(jù)已知條件可以得到△ABC是直角三角形，把四面體補(bǔ)成一個(gè)長(zhǎng)方體，則四面體的外接球就是長(zhǎng)方體的外接球，外接球的直徑就是長(zhǎng)方體的體對(duì)角線.

則（2R）2=SA2+AC2=16，所以R=2.

例5：已知四面體PABC的側(cè)面PAC與平面ABC垂直，∠ABC=90°，BC=2■，AB=2，且PA⊥PC，PA=PC，求異面直線PC與AB所成角的余弦值.

解答：把四面體補(bǔ)成如圖所示平行六面體，異面直線PC與AB所成角即為PC與CD所成角的補(bǔ)角的余弦值.

取AC中點(diǎn)M，PA=PC，則PM⊥AC，又因?yàn)槠矫鍼AC與平面ABC垂直，所以PM⊥平面ABC.

△ABC中，∠ABC=90°，AB=2，BC=2■，所以∠ACB=30°，AC=4.

△PAC中，PA⊥PC，PA=PC，AC=4，所以PM=2，PC=2■.

底面四邊形ABDC中，DM2=DC2+CM2-2DC·CM·cos120°，得到DM=2■.Rt△PMD中，PD=4.

△PCD中，cos∠PCD=■= -■.

所以異面直線PC與AB所成角的余弦值為■.

此題也可以用空間向量法解答，用補(bǔ)形能更好地體現(xiàn)線面關(guān)系.

三、把四面體補(bǔ)形成三棱柱

例6：已知某幾何體底面ABC是棱長(zhǎng)為1的等邊三角形，PA⊥平面ABC，PA=3，求該幾何體的外接球的半徑.

解答：將該四面體補(bǔ)形成一個(gè)三棱柱

四面體的外接球就是三棱柱的外接球.

先求三棱柱底面三角形外接圓半徑r=■·■=■.

又因?yàn)镻A⊥平面ABC，PA=3，

所以三棱柱的外接球半徑為R=■=■.

四面體的問(wèn)題可以通過(guò)補(bǔ)形變成正方體、長(zhǎng)方體乃至平行六面體的問(wèn)題.尤其在正方體和長(zhǎng)方體中，點(diǎn)線面的關(guān)系是我們所熟悉的. 一些幾何題的證明和求解，由原幾何圖形分析探究會(huì)比較煩瑣，通過(guò)補(bǔ)形填補(bǔ)成一個(gè)新的幾何圖形，能使原問(wèn)題的本質(zhì)得到充分的體現(xiàn)，解決起來(lái)比較容易. 本文著重討論四面體的補(bǔ)形問(wèn)題，希望窺一斑而知全豹，探究立體幾何中補(bǔ)形法這一重要的轉(zhuǎn)化策略.