對一道好題的多維解析與火熱思考

何雪冰

[摘? 要] 文章以一道實際應用題為例，探討并教會學生選擇解題路徑與方法.通過對一個問題的研究、一題多解的探討，引導學生將所學知識融會貫通，重在引導學生善于方法的總結與優化，讓學生學會主動歸納總結問題的各種解法，掌握處理各種問題的通性通法，通過一題多解最終實現多題一解.

[關鍵詞] 解法探析;通性通法;學會選擇;反思提升

最近筆者在高三年級進行高中數學二輪微專題復習時，遇到一道模考題，內涵豐富，立意深刻，著實是一道好題.本文就其解法做了一些探析與反思，拋磚引玉，期望能引起大家更多的思考.

■原題呈現

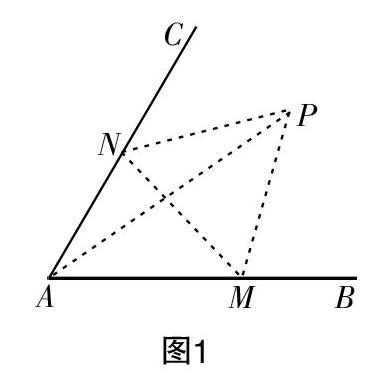
如圖1，經過村莊A有兩條夾角為60°的公路AB，AC，根據規劃擬在兩條公路之間的區域內建一工廠P，分別在兩條公路邊上建兩個倉庫M，N （異于村莊A），要求PM=PN=MN=2（單位：千米）. 如何設計，使得工廠產生的噪聲對居民的影響最小（即工廠與村莊的距離最遠）？

■解法探析

1. 構建三角函數

如圖1，設∠AMN=θ，在△AMN中，■=■.

因為MN=2，所以AM=■sin（120°-θ）.

在△APM中，cos∠AMP=cos（60°+θ）.

AP2=AM2+MP2-2AM·MP·cos∠AMP

=■sin2（120°-θ）+4-2×2×■·sin（120°-θ）cos（60°+θ）

=■sin2（θ+60°）-■sin（θ+60°）cos（θ+60°）+4

=■[1-cos（2θ+120°）]-■·sin（2θ+120°）+4

=-■[■sin（2θ+120°）+cos（2θ+120°）]+■

=■-■sin（2θ+150°），θ∈（0，120°）.

當且僅當2θ+150°=270°，即θ=60°時，AP2取得最大值12，即AP取得最大值2■.

解法評析：這種解法是此類問題的通性通法，利用正余弦定理確定邊角關系，關鍵在于恰當設角，建立已知量與未知量的函數模型，從而解決目標，但是對三角運算要求較高.

2. 構造直角三角形

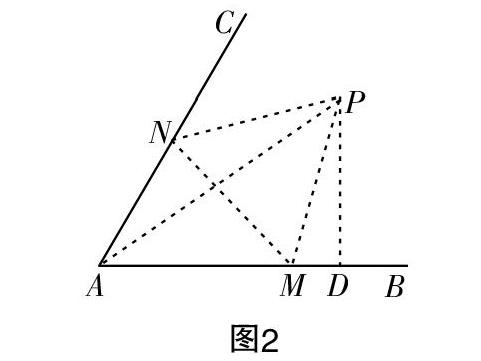
如圖2，設∠PMD=θ，在Rt△PMD中，

因為PM=2，所以PD=2sinθ，MD=2cosθ.

在△AMN中，∠ANM=∠PMD=θ，所以■=■，

AM=■sinθ，所以AD=■·sinθ+2cosθ（θ≥■時，結論也正確）.

AP2=AD2+PD2=■sinθ+2cosθ■+（2sinθ）2

=■sin2θ+■sinθcosθ+4cos2θ+4sin2θ

=■·■+■sin2θ+4=■sin2θ-■cos2θ+■

=■+■sin2θ-■，θ∈0，■.

當且僅當2θ-■=■，即θ=■時，AP2取得最大值12，即AP取得最大值2■.

此時AM=AN=2，∠PAB=30°

解法評析：方法2與方法1本質一樣，都是恰當設角構建三角函數模型，但是方法2利用化斜為直的思想，構造直角三角形搭建未知量與已知量的橋梁，從而使得運算簡捷一些.

3. 利用基本不等式

設AM=x，AN=y，∠AMN=α.

在△AMN中，因為MN=2，∠MAN=60°，

所以MN2=AM2+AN2-2 AM·AN·cos∠MAN，

即x2+y2-2xycos60°=x2+y2-xy=4.

因為■=■，即■=■，

所以sinα=■y，cosα=■=■=■.

cos∠AMP=cos（α+60°）=■cosα-■sinα=■·■-■·■y=■.

在△AMP中，AP2=AM2+PM2-2 AM·PM·cos∠AMP，

即AP2=x2+4-2×2×x×■=x2+4-x（x-2y）=4+2xy.

因為x2+y2-xy=4，4+xy=x2+y2≥2xy，即xy≤4.

所以AP2≤12，即AP≤2■.

當且僅當x=y=2時，AP取得最大值2■.

解法評析：通過三角關系建立二元等式，借助基本不等式求最值，這是求解最值十分重要的基本方法，難點在于能否構建二元等式，并且未知量較多.

4. 利用坐標法

如圖3，以AB所在的直線為x軸，A為坐標原點，建立直角坐標系.

設M（x■，0），N（x■，■x■），P（x■，y■）.因為MN=2，

所以（x■-x■）2+3x■=4.

MN的中點K■，■x■.

因為△MNP為正三角形，且MN=2.所以PK=■，PK⊥MN.

所以PK2=x■-■■+y■-■x■■=3，k■·k■=-1，即■·■= -1，

所以y■-■x■=■x■-■，所以y■-■x■■=■x■-■■.

所以1+■x■-■■=3，即■x■-■■=3，所以x■-■■=■x■.

因為x■-■>0，所以x■-■=■x■，

所以x■=■x■+2x■，所以y■=■x■.

所以AP2=x■+y■=2x■+■x■■+■x■=x■+4x■+2x■x■=4+4x■x■≤4+4×2=12，

即AP≤2■.

解法評析：坐標法即為圖形問題代數化，將部分思維量轉化為運算量，能夠降低思維難度，但是坐標運算復雜.

5. 矩陣變換法

如圖4，以AB所在的直線為x軸，A為坐標原點，建立直角坐標系.

設M（x■，0），N（x■，■x■），P（x■，y■）.

因為MN=2，所以（x■-x■）2+3x■=4. 即x■+4x■=4+2x■x■，

所以4+2x■x■≥4x■x■，即x■x■≤2.

因為△MNP為正三角形，且MN=2.所以PK=■，PK⊥MN.

■順時針方向旋轉60°后得到■.

■=（x■-x■，y■），■=（x■-x■，■x■）.

所以■? ?■-■? ■ x2-x1■x2=x0-x1 y0，即x■-x■=■（x■-x■）+■x■，y■= -■（x■-x■）+■x■. 所以x■=2x■+■x■，y■=■x■.

所以AP2=x■+y■=2x■+■x■■+■x■=x■+4x■+2x■x■=4+4x■x■≤4+4×2=12，

即AP≤2■.

解法評析：矩陣變換法給本題注入了一股清風，突出變換的作用，能夠將復雜的運算簡單化.但是由于高中階段對矩陣要求較低，很少有學生能想到用這個解法.

6. 平面幾何法

如圖5，由運動的相對性，可使△PMN不動，點A在運動. 由于∠MAN=60°，所以點A在以MN為弦的一段圓弧（優弧）上，設圓弧所在的圓的圓心為F，半徑為R，由圖形的幾何性質知：AP的最大值為PF+R.

在△AMN中，由正弦定理知：■=2R，

所以R=■，所以FM=FN=R=■. 又PM=PN，所以PF是線段MN的垂直平分線.

設PF與MN交于E，則FE2=FM2-ME2=R2-12=■，即FE=■.

又PE=■，所以PF=■，所以AP的最大值為PF+R=2■.

解法評析：平面幾何法讓人耳目一新，更加揭示本題的本質，從∠MAN=60°，MN=2這一組對角對邊為定值，也許能讓人聯想到正弦定理和三角形的外接圓，從而探尋到解題思路.只有平時經常增強圖形意識，強化讀圖、識圖、想圖、用圖的能力，才能不斷增強感覺，提升解題能力.

■反思感悟

對于數學解題，很多時候剛開始可能沒有思路，或許思路太多導致無從上手，那么此時需要我們能夠靜下心來認真讀題、冷靜分析，做出合理恰當的選擇. 平時解題時應當盡量用多種方法解題，通過對一道題的深入探究，回顧和深化相關的知識及解題思想方法，實現一類問題的解決，即通常我們說的通過一題多解，最終實現多題一解.

在掌握基本思想方法的同時，還要善于方法的選擇和優化，主動歸納、學會總結，這樣在遇到問題時，才會少走彎路，這樣的解題才更加有意義.