高中數學探究式教學的實踐研究

王光華

[摘? 要] 新課改風向標下，高中數學課堂教學更加關注學生探究能力和創新精神的培育. 探究式教學作為數學課堂中一種重要的教學方式，教師需依照學情展開研究式教學，引領學生探究知識形成的過程，探究數學概念，探究數學規律，助力學生的數學學習.

[關鍵詞] 探究性教學;數學概念;數學規律;本質

探究即探索，它是數學課堂中一種重要的教學方式. 數學探究就是以問題的解決為目標，以探究性問題為載體，以思考、討論、互動、自主、評價等活動方式為主線的一種學習活動. 而本文中所指的探究式教學特指的是一種課堂的教學方式，也是建構主義學習理論的一種教學實踐模式. 對比傳統教學模式，探究性教學更具有實踐性和開放性，利于學生的自主探究和學習. 下面筆者結合幾個教學片段，談談探究式教學的幾種類型，為學生的數學學習助力. ？搖

■探究知識形成過程

數學教學的過程不應僅僅是知識的匯聚或是方法的獲取，更需要的是對知識形成過程的探究. 基于此，學生的探究性學習品質自然需孕育在探究知識的形成過程中. 然而縱觀大量的課堂教學實踐，大部分學生還是習慣于“聽講”模式，缺乏數學探究的方法，而知識的建構又是建立在自身的感悟和反思之上的. 因此，教師需要通過“探究式教學”為前提和基礎，充分暴露自身的思維過程，進行探究示范，展示知識的形成和發展，使學生在耳濡目染中學會探究的策略與方法，獲得豐富的探究體驗，進一步地讓學生體會概念、公式、法則等結論的來龍去脈，探清知識本質，從而水到渠成地進行自我建構.

案例1：以“點到直線的距離公式”的探究為例

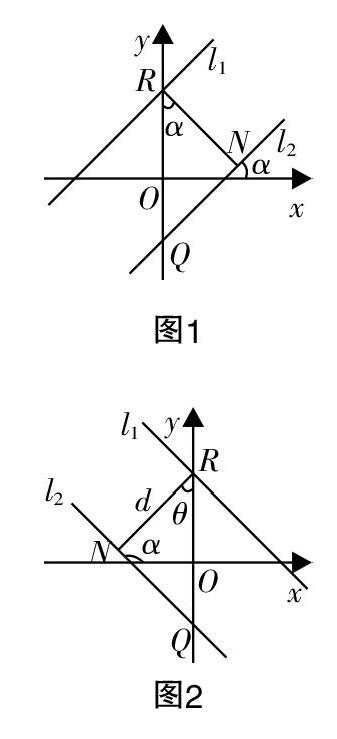
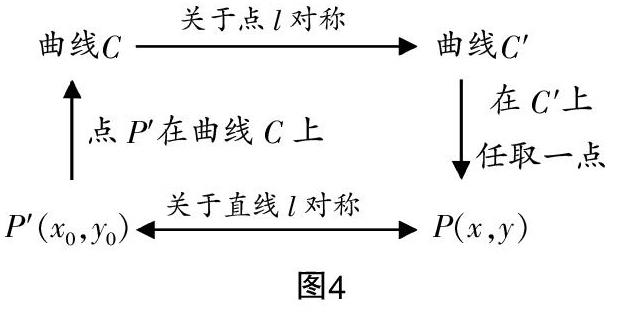
問題1：已知l■：y=kx+b■，l■：y=kx+b，且有l■∥l■，試求出l■，l■的距離d.

分析：畫出圖1和圖2，即可求出d=RQ·cos（π-α）=■.

問題2：“兩平行線間的距離公式”該如何向“點到直線的距離公式”轉化？

分析：由平行線間距離處處相等的原理，可在l■上任意取P（x■，y■），則有y■=kx■+b■，可得b■=y■-kx■，代入公式后可得d=■.

問題3：已知直線y=kx+b，點P（x■，y■），試求出點P到l的距離.

分析：只需將問題2中的b■轉化為b即可，則有d=■.

問題4：已知直線Ax+By+C=0，點P（x■，y■），試求出點P到l的距離.

分析：令k=-■，b=-■，再代入公式后進行整理，可得d=■. （注：當B=0時，公式同樣成立）

說明：本課內容的學習是該章節的重難點之一. 教材中是直接拋出了問題4，以引導學生的分析與求證. 當然以此展開的探究在知識和方法上也是一目了然的，但違背了學生的知識建構的過程，易造成學生學習中知識點的困惑，甚至于偏差. 以上案例中，教師精心設置了一個“問題鏈”來重組教材內容，使其更具有探索性和層次性;同時教師探究示范“問題1”，為學生的探究鋪路引航，逐漸將他們的探究引入深處，讓他們進行自主活動、發現和探究問題，經歷過程，建立起自己的探究經驗，探清其本質，完善學習結構.

■探究數學概念

在知識應用的層面上來看，數學概念是其典型標志，因此，在概念教學的過程中，教師需設計科學而合理的題組，并給予學生充足的時間和空間，讓學生嘗試和探索，探清概念的內涵，在嘗試中獲得新知，在探索中獲得感悟，學會一種良好的學習方式. 這樣一來，概念的得來是在學生的參與中獲得的，讓學生有了充分的體驗和感悟.

案例2：以“集合的含義”的探究為例

問題1：請模仿以下的敘述來介紹自己：我們家有爺爺、奶奶、爸爸、媽媽和我，我來自第一中學.

問題2：請班上所有學生按照性別分為兩組：一組為A組，一組為B組. 那么，你屬于A組還是B組呢？

問題3：請班上所有學生按照畢業于相同初中的學生站在一起，分成不同的組別，并以此進行編號. 那么，你屬于其中的哪個組別呢？

問題4：在以上三個問題中，“家庭”“男生”“女生”“學校”等概念均有什么共同點？

說明：通過以上的“問題串”，引領學生的數學思考，讓學生去體驗和感知，并以自己的語言去表達，在表達的基礎上逐步生成概念. 從現實生活中的實例出發，使學生快速理解和認識概念本身;從分組的數學活動開始，讓學生在參與和體驗之中寓教于樂，愉快而輕松地學習新知;從數學概念的本質展開，讓學生參與概念的由來過程，使其探清概念的內涵，為后續的學習打下堅實的基礎. 案例充分表明，學生探究起來興趣盎然并樂此不疲，為統領全課奠定了良好的基礎.

■探究數學規律

數學教學中不僅需要讓學生掌握知識，而且更應該關注學生認知能力的培養，使其在數學學習中洞悉數學規律，通過探究數學規律來解決實際問題. 對于規律的探索，本身就是發現問題和發展思維的過程，它可以架構知識間的聯系，優化已有知識結構，還可以開拓創新，打通學生的思維通道，利于學生的綜合發展. 因此，在探究式教學中，教師可以由淺入深地引領學生參與到規律探索中去，幫助其探清解題規律，以此實現思維和能力的共同發展.

案例3：以“對稱問題”的探究為例

問題1：已知點P（x■，y■）. （1）請結合圖像求出其關于原點的對稱點的坐標;（2）請結合圖像求出其關于x軸的對稱點的坐標;（3）請結合圖像求出其關于y軸的對稱點的坐標;（4）請結合圖像求出其關于直線y=x的對稱點的坐標;（5）請結合圖像求出其關于直線y=-x的對稱點的坐標.

分析：可將其分為中心對稱和軸對稱進行處理，進而得出結論.

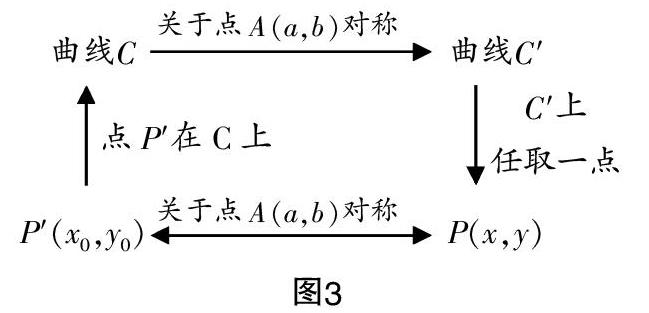
問題2：已知點P（x■，y■），試求出其關于A（a，b）的對稱點P′（x，y）的坐標.

分析：借助中點坐標公式，即可求得x=2a-x■，y=2b-y■.