基于無傳感器的永磁同步電機容錯控制

趙柏暄，張 希，錢 偉，張凱炯

(上海交通大學 機械與動力工程學院，上海 200240)

0 引 言

永磁同步電機因其具有功率密度高、效率高、調速范圍寬、轉矩波動小等優點而成為了電動汽車領域的首選[1]。永磁同步電機的矢量控制需要精確地檢測到轉子的位置信息，考慮到電動汽車中工作環境較為惡劣，旋轉變壓器被廣泛應用于電動汽車永磁同步電機的位置檢測中。

旋轉變壓器在檢測過程中存在故障隱患，這些故障會導致永磁同步電機轉矩波動甚至失控，進而會影響車輛行駛的穩定性，甚至會危及車輛安全[2]。因此，有必要采用容錯控制以保證電動汽車電驅動系統在旋轉變壓器發生故障時可以繼續運行。Hwang S H等針對旋轉變壓器的幅值不平衡和正交不完全故障設計了補償算法[3]，但該方法無法解決旋轉變壓器斷線和短路故障。將無位置傳感器控制作為旋轉變壓器的一種軟件冗余，是解決此問題的有效途徑。無位置傳感器控制算法主要有兩類：適用于中高速區的反電動勢觀測器法，包括遞歸最小二乘法、擴展卡爾曼濾波器、模型參考自適應法和滑模觀測器等；適用于零速、低速區的高頻信號注入法，可分為旋轉高頻電壓注入法和脈振高頻電壓注入法[4]。目前，并沒有一種無位置傳感器算法可以在全速度范圍內對轉子位置進行估計。無位置傳感器控制技術在永磁同步電機容錯控制方面的應用也取得了一定的進展。Demba Diallo等針對車用感應電機設計了一種容錯控制算法，該算法由間接矢量控制、基于自適應磁鏈觀測器的無傳感器控制及開環V/f控制組成，并提出了一種故障診斷策略，根據診斷結果切換控制算法[5]。Ahmad Akrad等針對永磁同步電機使用擴展卡爾曼濾波器和自適應反電動勢觀測器對轉子位置和速度進行觀測，并基于最大似然法設計了故障診斷和容錯控制算法[6]。文建平將旋轉變壓器位置偏差故障補償算法與基于微分代數觀測器的無位置傳感器控制算法進行了結合[7]。Gilbert Foo Hock Beng等使用自適應磁鏈觀測器與脈振高頻電壓信號注入法，實現了全速度范圍的容錯控制[8]。然而，由于鐵心磁飽和、交叉耦合效應及溫度等因素的影響，d，q軸電感及永磁體磁鏈會發生變化[9]。傳統的觀測器算法依賴于電機參數，當電機參數發生變化時，可能會造成位置估計誤差較大等問題。

本文首先分析了旋轉變壓器故障的影響。其次，針對旋轉變壓器故障設計了容錯控制，在高速區采用基于柔性開關函數滑模觀測器的無位置傳感器控制算法，在低速區采用脈振高頻信號注入法的無位置傳感器控制算法及低、高速區過渡算法，并根據估計結果設計了故障診斷算法。最后通過仿真和實驗驗證了該容錯控制算法的有效性。

1 旋轉變壓器故障影響分析

當旋轉變壓器存在故障時，可認為測量轉子位置與實際轉子位置存在角度誤差，此時永磁同步電機d，q軸電流可表示:

永磁同步電機的電磁轉矩方程:

Te=1.5p[ψfiq+(Ld-Lq)idiq]

(2)

將式(1)代入式(2)，旋轉變壓器故障狀態下永磁同步電機的電磁轉矩方程:

Te=1.5pImcosθerr[ψf+(Ld-Lq)Imsinθerr]

(3)

式中：Te為電磁轉矩；p為電機極對數；ωr為電機角速度；ψf為永磁體磁鏈；Im為相電流幅值。

由式(3)可知，在旋轉變壓器存在故障時，當偏差角度較小時會造成電機輸出轉矩波動，嚴重時則可能導致電驅動系統失控，進而會影響車輛的動力性、舒適性和安全性。

2 容錯控制

2.1基于高頻信號注入的無位置傳感器控制算法

假設繞組中的感應電動勢為正弦波，在d-q軸同步坐標系中，PMSM的數學模型:

(4)

式中：ud，uq為d,q軸定子電壓；id，iq為d,q軸定子電流；R為各相定子電阻；Ld，Lq為d,q軸定子電感。

在低速區，電壓注入信號頻率遠高于基波頻率，反電動勢可忽略不計，同時忽略定子電阻壓降，則PMSM的數學模型可改寫：

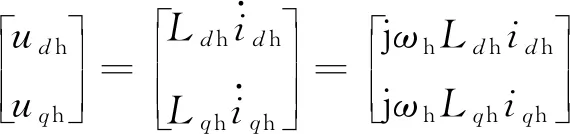
(5)

式中：udh，uqh，idh，iqh，Ldh，Lqh分別為d，q軸高頻電壓、電流和電感。

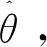
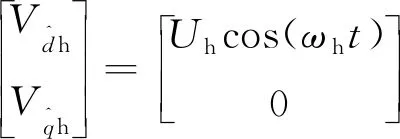
(6)

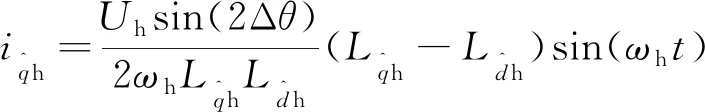
(7)

將式(7)與sin(ωht)相乘，并通過低通濾波器濾除高頻分量，可以得到:

(8)

當Δθ足夠小時，可認為:

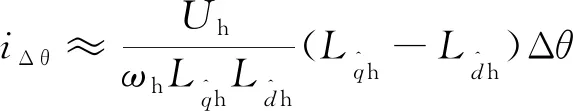
(9)

為獲取轉子速度和位置信息，觀測器設計如圖1所示。

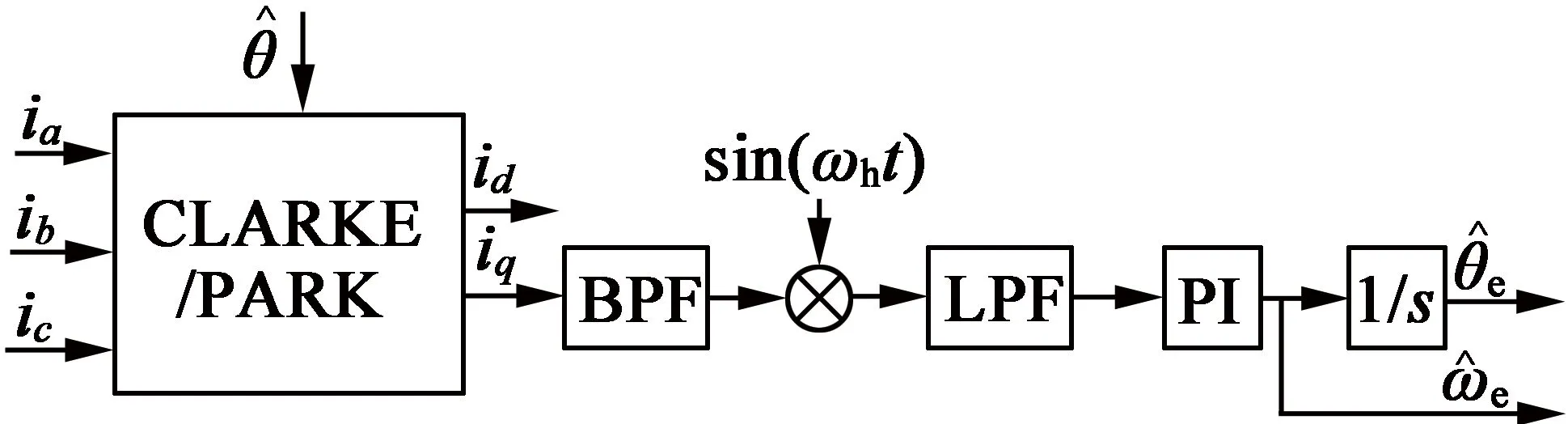
圖1 脈動高頻電壓信號注入法轉子位置觀測器

2.2基于柔性開關滑模觀測器的無位置傳感器算法

在α,β坐標系下永磁同步電機的數學模型:

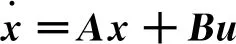
(10)

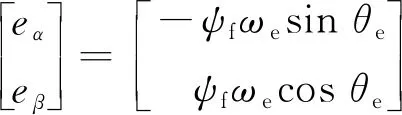
(11)

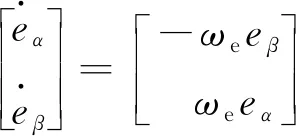
(12)

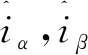
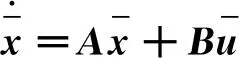
(13)

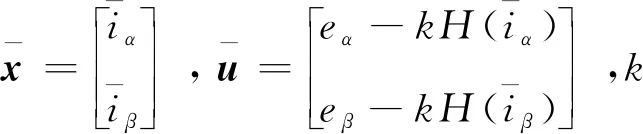
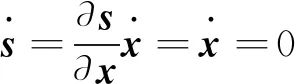
(14)

函數f2∈(0,1]，當UAV的飛行路徑上存在點分別與N個信息采集點的坐標之間的距離都在讀寫器的識別距離之內(即對?C點都?點Xi滿足1≤r)時，f2的值較小，即所求得的路徑較短。

電機轉子位置估計值：

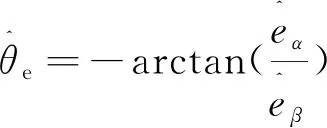
(15)

為避免觀測器中低通濾波器引起的轉子位置估計值相位滯后于實際位置的問題，可采用鎖相環提取轉子位置信息。基于柔性開關滑模觀測器及鎖相環的結構如圖2所示。

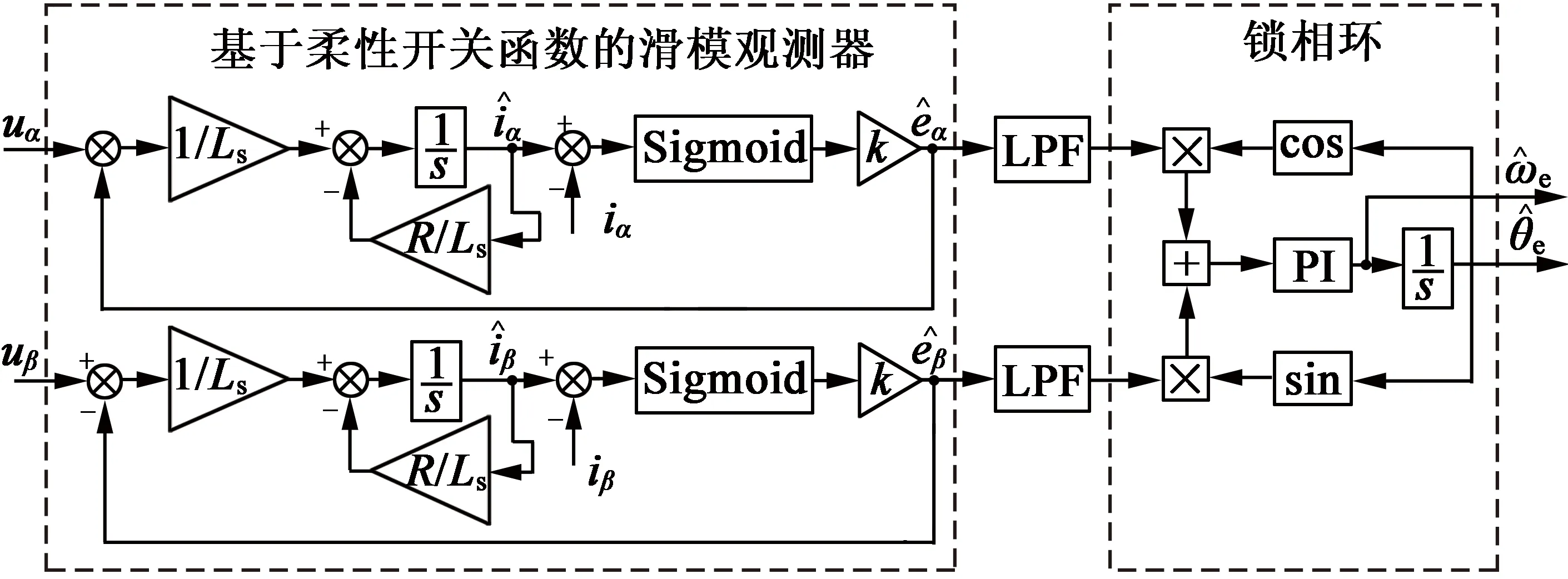
圖2 基于柔性開關函數的滑模觀測器及鎖相環結構

2.3低、高速區過渡算法

如上文所述，為實現全速度范圍的無傳感器控制，需要在低速區和中高速區分別采用不同的算法。由于脈振高頻信號注入法與基于柔性開關滑模觀測器的估計結果之間存在誤差，直接切換可能會在切換點附近產生振蕩。通過權重分配函數作為過渡算法可實現低速區與高速區之間的平穩過渡，權重分配函數設計如下：

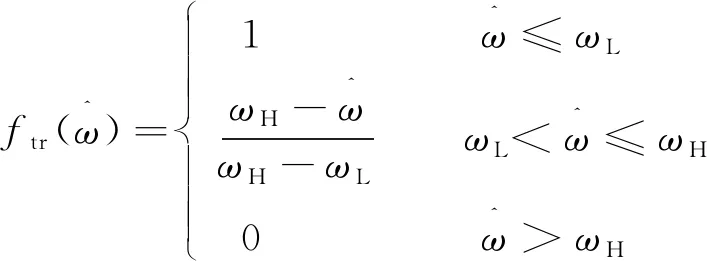
(16)

式中：ωL為低速區切換速度點；ωH為高速區切換速度點。

(17)

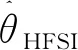
圖3 高、低速區過渡算法結構

該過渡算法以估計速度值為過渡算法介入依據，當速度低于低速區切換點時，采用脈振高頻信號注入法的估計值；當速度高于高速區切換點時，采用基于柔性開關滑模觀測器的估計值；當速度介于兩者之間時，進入過渡算法。對于不同車型，該算法均有效，但由于驅動電機不同，切換點需根據具體電機型號確定。

電動汽車傳動系通常由單擋減速器或雙擋變速器、主減速器及差速器組成。在車輛穩定運行狀態下，驅動電機轉速和位置可由車速傳感器測量結果根據傳動系傳動比計算得到:

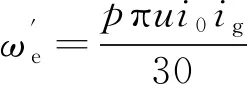
(18)

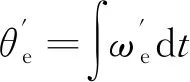
(19)

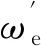
所設計的故障診斷判據如下:

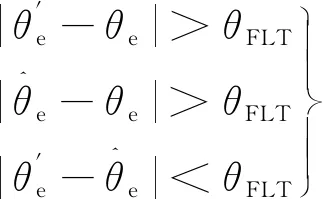
(20)

θFLT為位置誤差容許值。當轉子位置滿足式(20)時，則可認為旋轉變壓器故障，此時使用無位置傳感器算法估計值代替旋轉變壓器測量值，實現容錯控制。

3 仿真與實驗結果

3.1仿真結果

通過MATLAB-Simulink與CarSim軟件建立聯合仿真模型。為驗證算法的有效性，在仿真測量角度中加入一個偏差角度θerr。圖4為不采用容錯控制條件下，在0.5 s時旋轉變壓器發生故障的運行情況。圖4中,從上至下分別為電機轉子位置、電機輸出轉矩、車輛縱向加速度。當故障發生時，電機輸出轉矩波動，進而引起車輛縱向加速度波動，對車輛動力性和舒適性造成不良影響。圖5為采用容錯控制條件下，在發生故障時電機及車輛運行情況。圖5中,從上至下分別為電機轉子實際位置和估計位置、轉子位置估計誤差、電機輸出轉矩、車輛縱向加速度。由圖5可知，轉子估計位置與實際位置誤差較小，在平穩狀態下誤差小于0.2 rad,電機與車輛運行平穩。

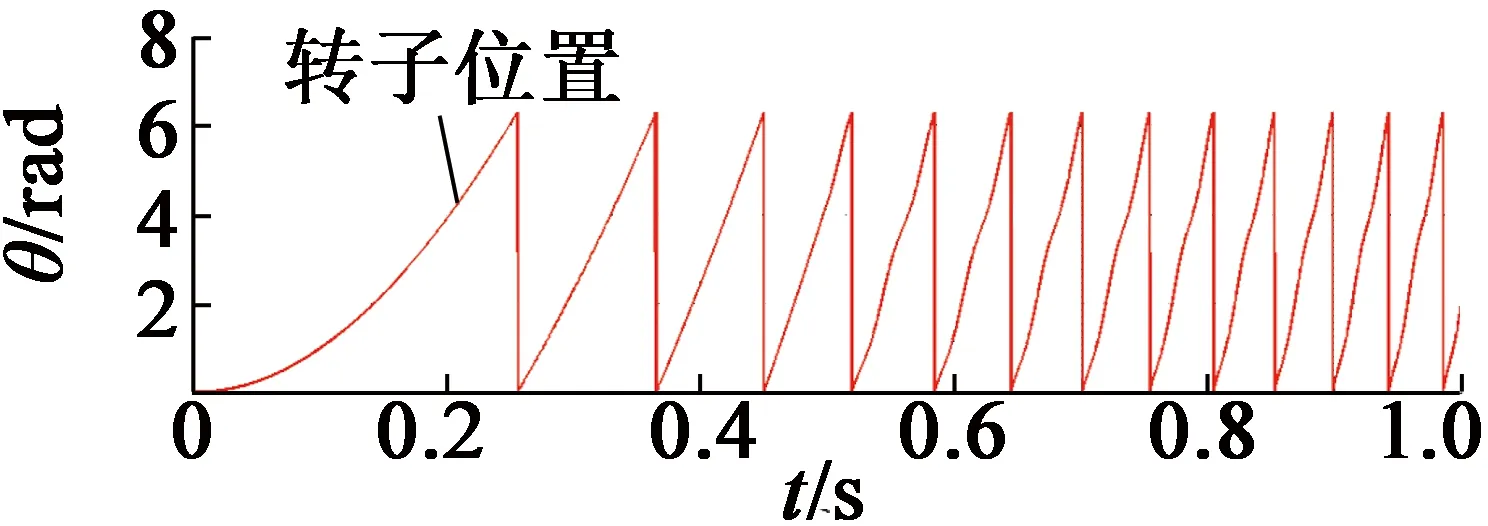
(a) 電機轉子位置

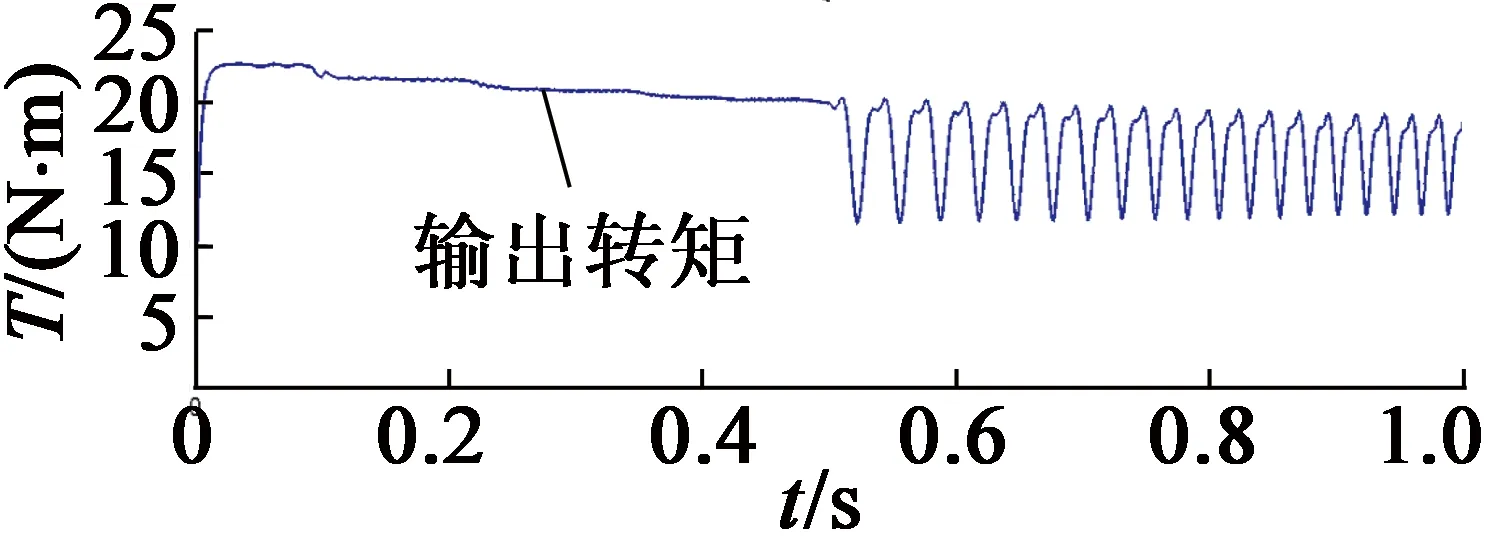
(b) 電機輸出轉矩

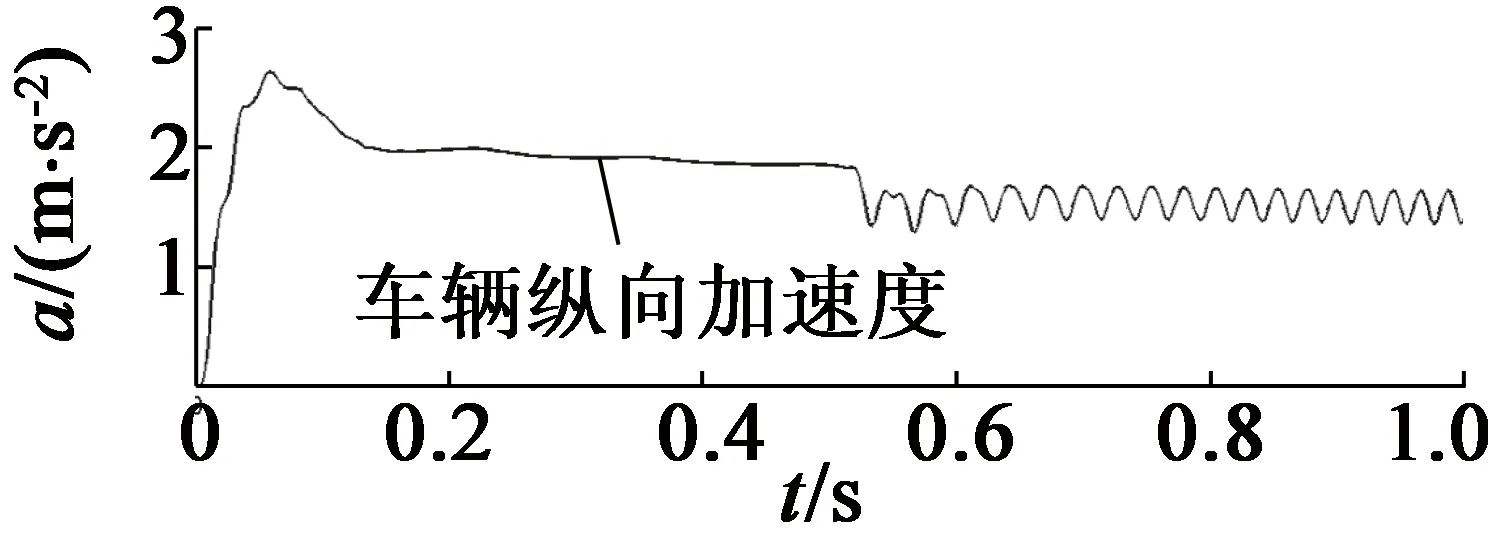
(c) 車輛縱向加速度圖4 不采用容錯控制運行情況

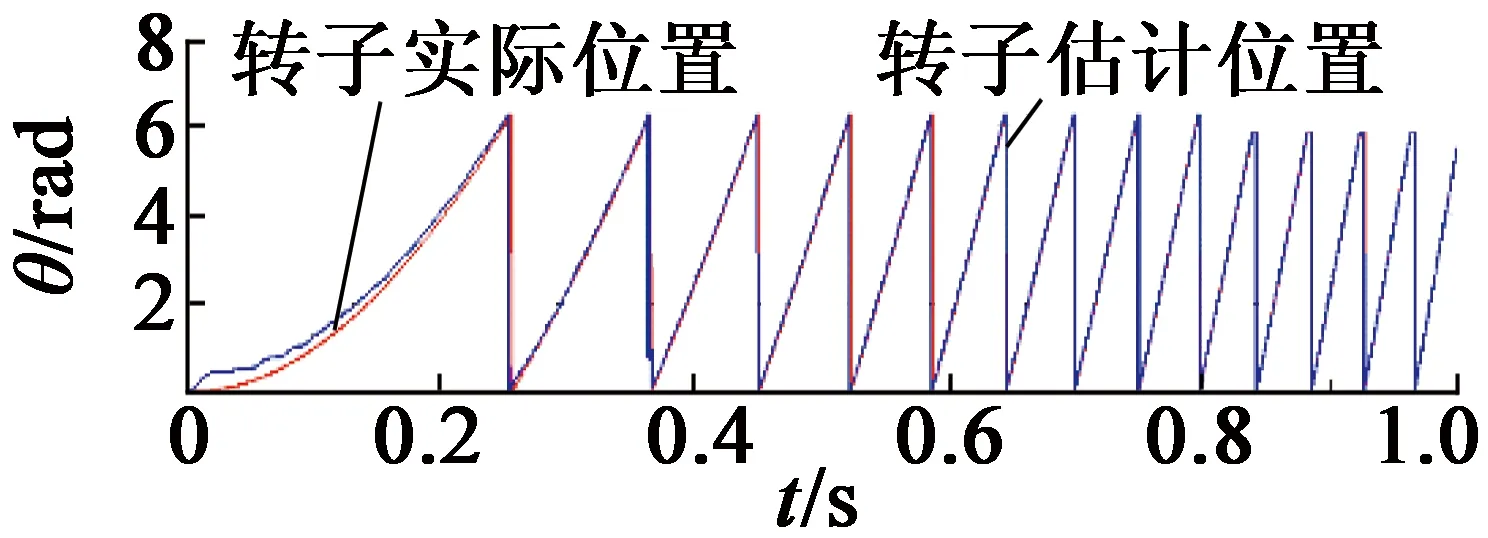
(a) 電機轉子實際位置和估計位置

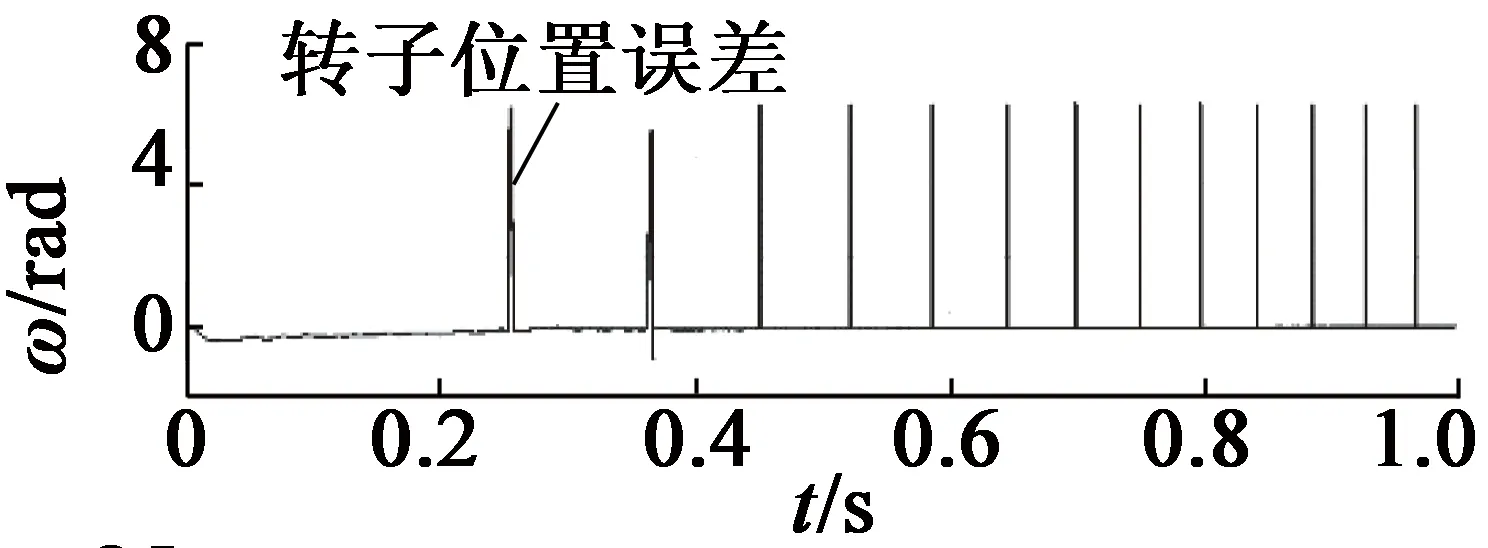
(b) 轉子位置估計誤差

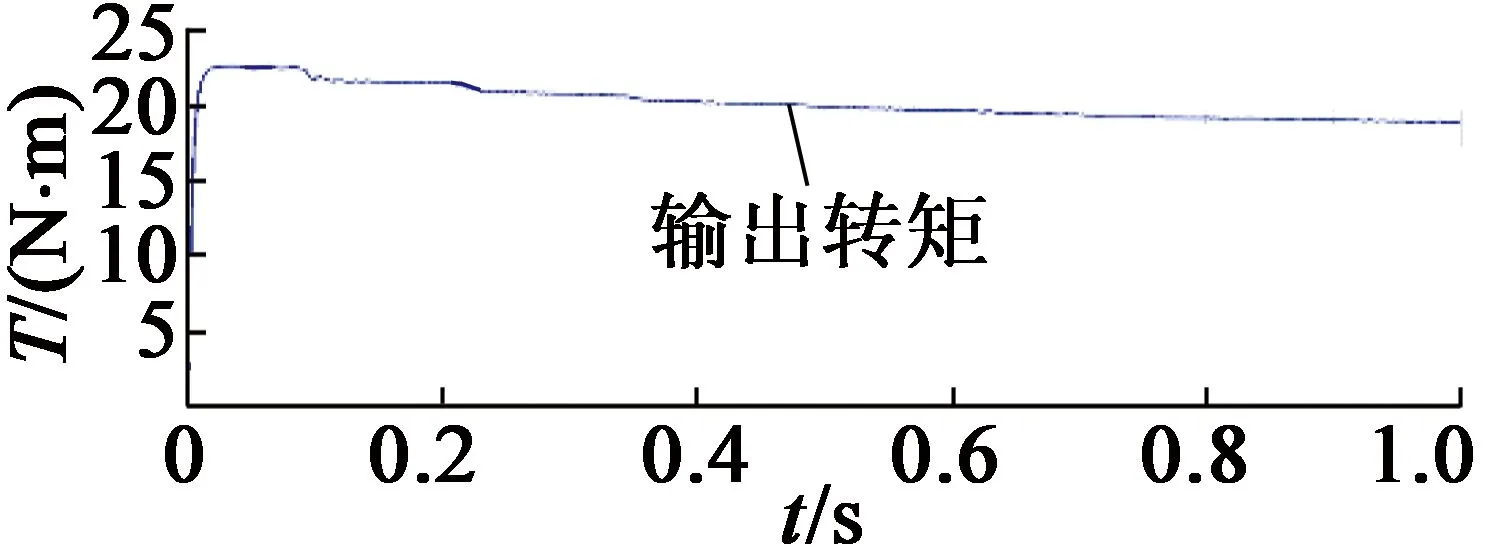
(c) 電機輸出轉矩

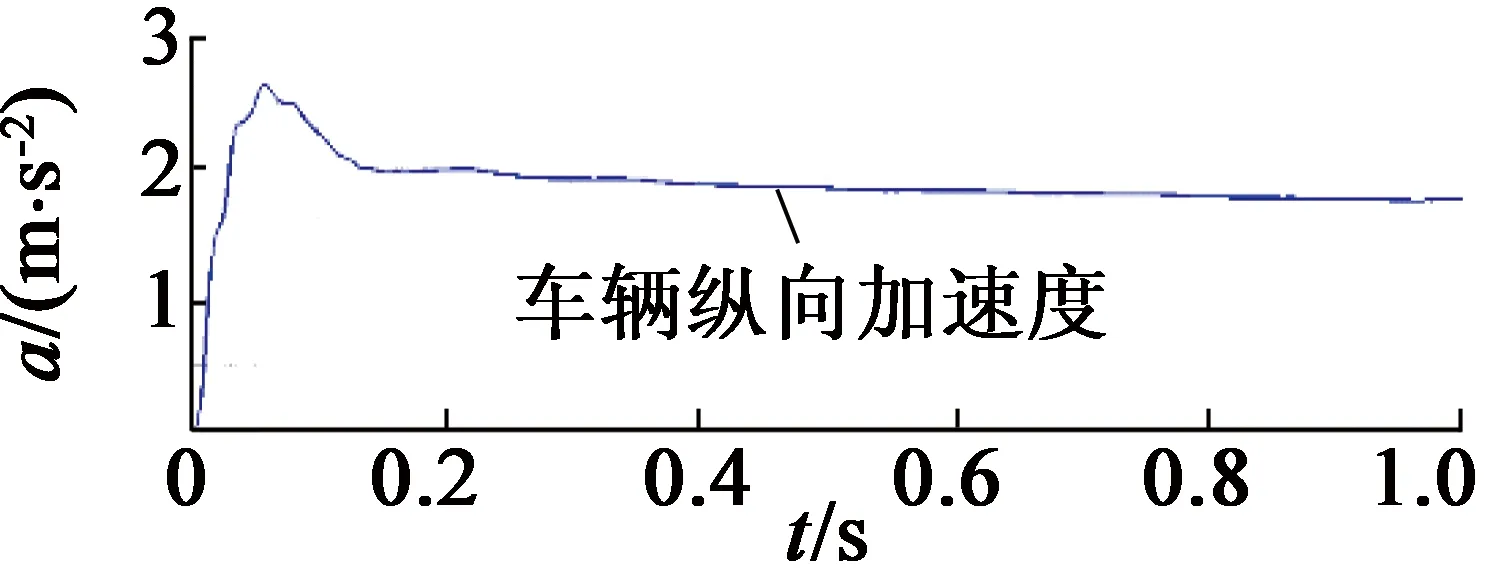
(d) 車輛縱向加速度圖5 采用容錯控制運行情況

3.2實驗結果

使用Micro-AutoBox及1 kW永磁同步電機搭建硬件平臺，對所提出的算法進行驗證。以一個旋轉變壓器作為電機轉子位置傳感器，以另一個旋轉變壓器采樣的位置信息模擬由車速傳感器計算得到的轉子位置信息，結果如圖6所示。

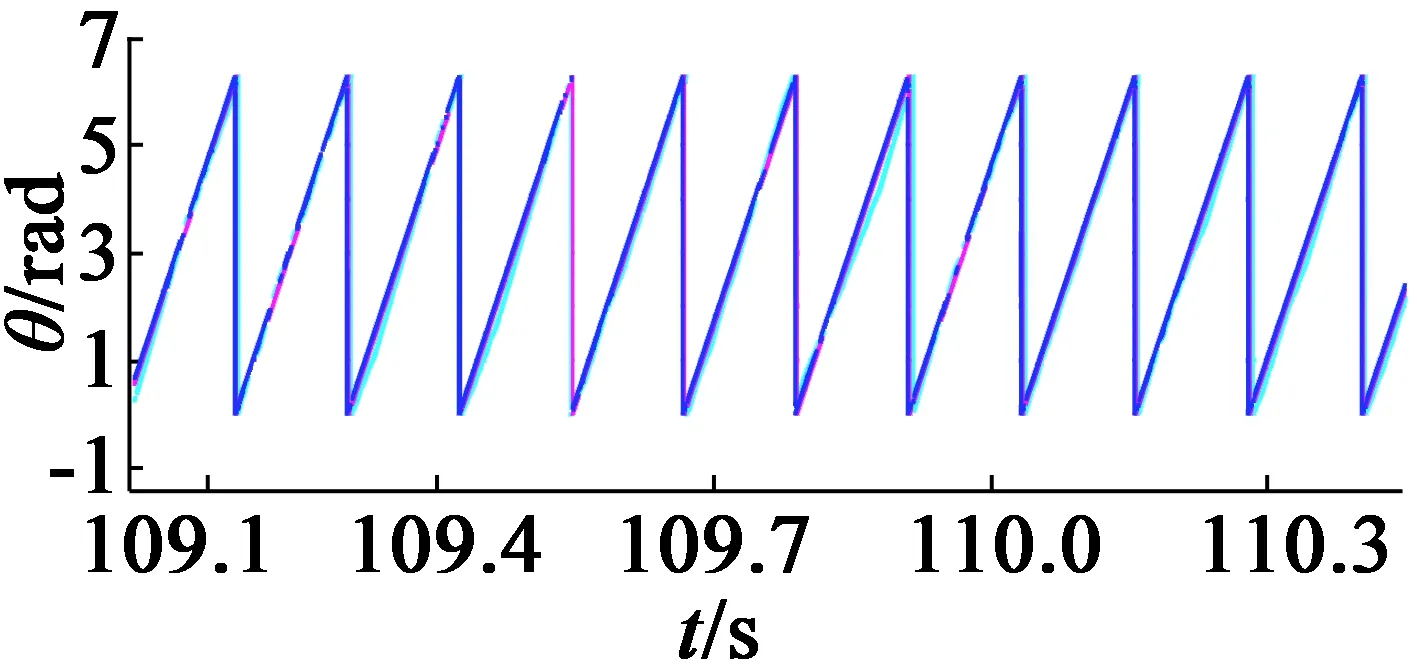
(a) 轉子位置估計實驗結果

從圖6可以看出，估計結果與旋轉變壓器測量結果之間誤差較小，誤差主要由傳感器測量誤差、系統誤差及算法中積分累積誤差造成。當故障發生時，容錯控制可替代旋轉變壓器提供轉子位置信息，維持電機平穩運行。在實際車輛中可采用嵌入式系統作為運行平臺，只需在原有電機控制算法中加入該算法，不會額外增加硬件成本。

4 結 語

本文基于脈振高頻電壓信號注入法及柔性開關滑模觀測器設計了永磁同步電動機無傳感器控制算法，實現了對轉子位置信息的準確估計，并根據估計結果設計旋轉變壓器故障容錯控制算法。仿真及實驗結果表明，當不采用容錯控制時，旋轉變壓器故障會對電動汽車電驅動系統及車輛的動力性、穩定性和安全性產生嚴重危害，本文容錯控制算法可有效避免這一問題。