雙向循環荷載下的單樁基礎累積側向位移

胡安峰， 肖志榮， 江進華， 付 鵬， 南博文

（1.浙江大學 濱海和城市巖土工程研究中心；軟弱土與環境土工教育部重點實驗室，杭州310058；2.浙江科技學院 土木與建筑工程學院，杭州310023）

隨著經濟的不斷發展，樁基礎在港口碼頭、跨海大橋等工程中應用越來越廣泛，這類樁基礎破壞機理和變形情況比傳統樁基更為復雜.車輛等交通荷載產生豎向作用，風、波浪等產生水平向作用，而且這些荷載作用為長期循環，使樁基容易產生累積變形.因此，研究豎向和水平循環荷載作用下樁基礎的累積側向位移意義重大.

國內外學者對水平循環荷載作用下樁基變形特性做了大量研究.樁基礎側向變形分析方法最普遍的是美國石油協會（API）[1]建議的p－y曲線分析法，但在水平循環荷載作用下樁基側向位移分析中，API建議的折減系數不能體現循環次數對累積變形的影響.Poulos[2]在采用p－y曲線法研究樁基循環累積變形時考慮了樁周土體強度和剛度隨循環次數衰減的影響，并給出了循環荷載作用下土體強度與剛度弱化因子的計算曲線.Rosquoet等[3]進行了一系列水平循環加載下樁基特性試驗，得出了循環荷載大小與樁身循環變形之間的關系表達式.朱斌等[4]進行了砂土中大直徑單樁水平受荷試驗，提出了與循環應力比相關的p－y曲線循環弱化因子和相應的樁基累積變形分析方法.郭玉樹等[5]提出了通過室內循環三軸試驗的結果來分析單樁基礎在水平循環荷載下變形的方法.羅如平等[6]通過開發有限元用戶子程序將剛度衰減模型嵌入到數值分析中，研究了荷載特性與循環次數對樁基累積水平變形的影響.

港口碼頭和跨海大橋等工作環境復雜，樁基礎同時承受水平和豎向循環荷載作用，但以上研究在分析樁基累積側向變形時沒有考慮豎向循環荷載的影響.Parvin等[7]利用數值模擬和模型試驗，分析了水平和豎向循環荷載耦合作用下單樁的特性，表明樁身軸力、樁身彎矩比單向加載時都更大；左殿軍等[8]利用數值模擬研究了水平和豎向循環荷載作用下碼頭群樁基礎的受力特性；但兩者都沒有考慮樁周土體循環弱化發生剛度衰減的特性.本文基于室內循環三軸試驗數據，建立考慮雙向循環荷載下的軟黏土剛度衰減模型，利用商業有限元軟件Abaqus進行二次開發，通過用戶子程序將剛度衰減模型嵌入到有限元分析中，研究豎向和水平循環荷載耦合作用下單樁基礎的累積側向位移特性.

1 剛度衰減模型

許多學者研究了土體在循環荷載作用下的特性，提出了一些軟化模型.Idriss等[9]最早提出了軟化指數δ的概念，即土體切變模量在第N次與第1次循環時的比值，建立了軟化指數與循環次數關系的表達式：

式中：d為軟化參數.Yasuhara等[10]在研究砂土循環特性時，提出了軟化指數和循環次數之間的半對數表達式：

王軍等[11]開展了飽和軟黏土的循環三軸試驗，發現δ與lgN之間并不是簡單的線性關系，而是存在較明顯的曲線關系，因而提出公式如下：

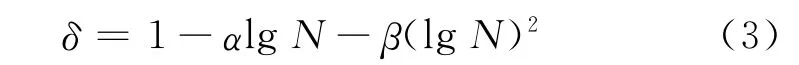
式中：α，β為軟化參數.王軍等[12]又研究了雙向循環荷載作用下飽和軟黏土的軟化特性，對土樣同時施加徑向和軸向正弦循環荷載如圖1所示.

圖1 雙向正弦循環荷載曲線[12]Fig.1 Bidirectional sinusoidal cyclic loadings[12]

圖中p0為圍壓，σdh與σdv分別為徑向與軸向循環應力，循環偏應力σd＝σdv－σdh.為了便于研究，分別定義了循環偏應力比與徑向循環應力比：

式中：τu為土體不排水強度.文中分析了循環偏應力、徑向循環應力對軟化參數的影響，考慮雙向循環荷載作用下土體的軟化情況，利用式（3）建立了軟化模型.雖然考慮了rc和Rc對δ的影響，但模型公式復雜，擬合參數較多，難以確定，在實際工程中應用難度較大.

基于此，本文在其試驗數據基礎上對軟化參數α和β進行重新擬合，得到較簡潔實用的關系式如下，從而改進軟化模型.

式中：a，b，c均為擬 合 參 數，分 別 為0.010 34，－0.044 52，0.485 21.圖2所示為修正剛度衰減模型與實測數據的對比.從圖中可以看出，修正剛度衰減模型曲線與實測數據點吻合得較好，發展變化趨勢相同，進一步說明了本文剛度衰減模型的正確性.

圖2 修正剛度衰減模型Fig.2 Modified model of stiffness degradation

2 數值模擬

2.1 建立模型

在樁土模型中，飽和軟黏土地基采用 Mohr－Coulomb彈塑性模型，參照文獻[13]可得相應參數.樁體材料為混凝土，樁基采用線彈性模型，土體及樁基模型參數如表1所示.

通過有限元軟件Abaqus建立三維樁土有限元模型.由于模型及受力的對稱性，樁土模型采用半圓柱體.圖3所示為數值計算模型，單樁直徑D＝1m、樁長L＝20m，為了避免模型邊界條件對數值模擬結果的影響，樁基中心距水平向邊界和樁底距地基底部的距離都取15倍樁徑[14]，樁土之間建立摩擦接觸，摩擦因數為tan（0.75φ）.受荷時樁土模型如圖4所示.其中，y為樁頂側向位移，Fh與Fv分別為水平循環荷載和豎向循環荷載.

表1 土體及樁基模型參數Tab.1 Model parameters of soil and pile

圖3 樁土數值計算模型Fig.3 Numerical simulation pile－soil model

圖4 受荷時樁土模型剖面圖Fig.4 Profile of pile－soil model under loadings

2.2 剛度衰減模型的實現

建立樁土模型，進行地應力平衡后同時對單樁施加水平循環荷載和豎向循環荷載.要在有限元分析中實現剛度衰減模型，需執行以下3個步驟.

（1）輸出施加循環荷載前后每個土體單元的最大主應力和最小主應力，即σ（1）1、σ（1）3與σ（2）1、σ（2）3.

（2）計算出σ（2）1與σ（1）1和σ（2）3與σ（1）3的差值，即分別得到σdv和σdh；然后算出循環偏應力σd.

（3）由σd和σdh根據式（4）和（5）求得每個土體單元所受的循環偏應力比與徑向循環應力比，再依次利用式（6）、（7）和（3）計算所有土體單元在雙向循環荷載作用下的軟化指數，最后通過子程序來實現土體剛度衰減模型在有限元分析中的應用.

3 有限元模型的驗證

Liao等[15]在近海軟黏土中開展了不同水平循環荷載作用下PVC管樁側向位移發展的室內模型試驗.在模型試驗中，樁長1 000mm，嵌入深度700 mm，樁徑為50mm，壁厚5mm，黏土重度為17kN／m3，模型樁的水平靜力極限荷載為100N.采用本文的方法，建立和模型試驗參數一致的有限元模型，計算單樁在不同水平循環荷載下的累積側向位移，再和模型試驗結果比較，如圖5所示.從圖中可以看出，在水平循環荷載作用下，本文結果比原試驗略小一些，但發展變化的規律相同.同時，在N＝1 000后，側向位移發展趨于平穩.這表明本文提出的剛度衰減模型可用于研究軟黏土中單樁基礎的側向位移問題.

圖5 本文模擬與模型試驗結果對比Fig.5 Comparison between the proposed model and model test

4 雙向循環荷載下樁基側向位移分析

研究雙向循環荷載作用下樁基側向位移，需要先確定樁基的水平極限承載力Fhu和豎向極限承載力Fvu.參考Zdravkovi＇c等[16]研究方法，基于樁頂水平變形0.1D來確定Fhu，根據建筑樁基技術規范[17]可以確定Fvu.為模擬雙向循環荷載作用下單樁基礎受力狀態，在豎向和水平向同時施加正弦規律變化的循環荷載如下.

式中：w1，w2代表荷載頻率；t為加載時間；Fvc，Fhc分別是豎向循環荷載幅值和水平循環荷載幅值.借鑒既往研究方法[18－19]，取w1＝w2＝1Hz，定義豎向循環荷載比η＝Fvc／Fvu，水平循環荷載比λ＝Fhc／Fhu.取不同的循環荷載比，進行不同幅值循環荷載作用下單樁基礎累積側向位移研究：η＝0.1，0.2，0.3，0.4，0.5；λ＝0.1，0.2，0.3，0.4，0.5，0.6.

4.1 雙向循環荷載下樁頂側向位移的發展

豎向循環荷載幅值恒定（η＝0.2）時，改變水平循環荷載幅值，樁頂累積側向位移的發展情況如圖6所示.從圖中可以看出，當水平循環荷載較小時（λ＝0.1）側向位移基本保持不變，累積位移不足0.01m.由此可知存在最小水平循環荷載比λmin，當λ≤λmin時側向位移并不隨著循環次數增大而累積.當λ從0.2到0.5時，側向位移隨循環次數增大而迅速發展，在N＝1 000后發展變緩，最后趨于穩定.因此，水平循環荷載產生的循環效應主要集中在循環周期的前面階段，朱斌等[4]在砂土模型試驗中也得到類似規律.當λ＞0.5時，樁頂側向位移隨著循環次數急劇增大，樁頂側向位移并不趨于平穩.基于此，表明存在最大水平循環荷載比λmax，從控制變形的角度分析，λ應控制在0.5以下.

圖6 不同水平循環荷載下的樁頂側向位移Fig.6 Lateral displacements of pile head under various lateral cyclic loadings

圖7 不同豎向循環荷載下時樁頂側向位移Fig.7 Lateral displacements of pile head under various vertical cyclic loadings

圖7所示當λ＝0.5時，不同豎向循環荷載下樁頂累積側向位移的發展情況.如圖所示：η為0.2和0.3時樁頂側向位移開始時增長較快，后期逐漸趨于平穩；同時隨著η增大，樁頂側向位移的發展速度增快，而且達到穩定時所需要的循環次數也越大.例如η＝0.2時，位移趨于穩定需要約1 000次，然而η＝0.4時，循環1 000次后累積位移仍持續增長，與圖6中水平循環荷載作用下N＝1 000后位移趨于平穩有所不同，說明豎向循環荷載影響樁頂側向位移的發展，推遲其平穩階段.當η＝0.5時，樁頂位移持續增大，y／D超過0.1時樁基已經被破壞.因此，當豎向與水平循環荷載都比較大時（λ＝0.5，η＝0.5），樁基礎累積位移發展迅速，位移值較大，樁基容易破壞，在實際工程中應避免雙向循環荷載都較大的情況.

雙向循環荷載作用下樁頂累積側向位移如圖8所示（N＝10 000）.當水平循環荷載較小時（λ＝0.1），樁頂側向位移很小且幾乎不變，說明水平循環荷載較小時豎向循環荷載的增大對樁頂側向位移影響很小.當水平循環荷載較大時（λ為0.2～0.5），隨著η增大，樁頂側向位移不斷增長，而且發展速度加快.豎向循環荷載比η從0.1到0.2時，樁頂側向位移增長較小，但η為0.2～0.5時，樁頂側向位移增長迅速，這說明豎向循環荷載比對樁基累積變形的影響存在一個界限值ηlim.朱斌等[19]在砂土中豎向循環受荷單樁的沉降模試型驗中也發現類似規律.驗證了本結論的正確性.

圖8 雙向循環荷載下的樁頂側向位移Fig.8 Lateral displacements of pile head under bidirectional cyclic loadings

4.2 單向與雙向循環荷載下樁頂側向位移的對比

N＝10 000次時，樁頂施加豎向靜載（0.3Fvu）與豎向循環荷載（η＝0.3）下的樁頂累積側向位移對比情況如圖9所示.由圖可見，當水平循環荷載較小時，兩者位移相近，當水平循環荷載較大時，豎向靜載條件下的側向位移明顯小于豎向循環荷載條件下的側向位移，且差距不斷增大.這是因為單樁受到雙向循環荷載耦合作用時，樁周土雙向受荷，雙向循環荷載作用下土體的強度比單向循環荷載作用下強度低[20].循環荷載較小時，應變發展緩慢，土體的應變較小，土體內部結構尚未破壞，故而兩者樁頂側向位移相近.循環荷載增大時，雙向受荷土體的應變迅速發展，土體內部結構較早開始被破壞，出現應變軟化現象，剛度不斷減小，故而樁基變形更大.

圖9 豎向靜載與豎向循環荷載下的樁頂側向位移Fig.9 Lateral displacements of pile head under vertical static and cyclic loadings

4.3 不同豎向循環荷載下的樁身側向位移

不同豎向循環荷載下樁身側向位移的發展情況如圖10所示（λ＝0.3，N＝10 000），其中z為樁基的豎向坐標.可以看出，η為0.1和0.2時，位移零點的位置在埋入深度為10m左右，之后隨著η的增大，位移零點的位置不斷下移，說明豎向循環荷載的增大加深了樁土變形的區域.同時，樁身側向位移也隨著η的增大而不斷發展，η＝0.1和0.2時，位移曲線基本重合，而η＝0.3的零點以上側移比η＝0.2的零點以上側移發展更迅速，說明豎向循環荷載對樁基變形的影響存在一個界限值.

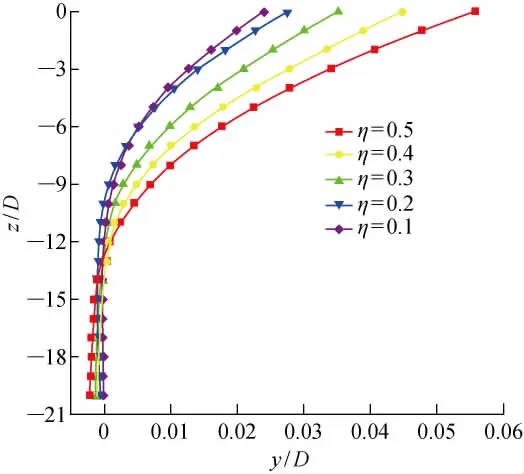
圖10 不同豎向循環荷載作用下的樁身側移Fig.10 Lateral displacements of pile under various vertical cyclic loadings

5 結語

本文建立了基于雙向循環受荷的軟黏土剛度衰減模型，通過用戶子程序將剛度衰減模型嵌入到有限元模型分析中，研究豎向和水平循環荷載耦合作用下單樁基礎的累積側向位移特性，得到如下結論：

（1）水平和豎向循環荷載耦合作用下，樁周土體雙向受荷，應變發展迅速，剛度不斷減小，易出現應變軟化現象，使得樁頂側向位移相比于只受水平循環荷載下的位移更大.循環加載一定周期后，樁頂累積側向位移逐漸趨于平穩，但豎向循環荷載的增大會推遲其平穩階段，使其達到平穩階段的循環周期增大.

（2）水平循環荷載比存在臨界值λmin和λmax.當λ≤λmin時，樁頂側向位移不會隨著循環加載而累積.當λmin＜λ≤λmax時，循環加載前期樁頂累積側向位移隨著循環次數增大而增大，后期逐漸趨于平穩.當λ＞λmax時，樁頂累積側向位移迅速增長，后期并不趨于平穩.

（3）當水平循環荷載較小時，豎向循環荷載對樁頂累積側向位移影響不大.當水平循環荷載較大時，豎向循環荷載對累積側向位移的影響存在一個界限值，即ηlim.豎向循環荷載比小于該值時，豎向循環荷載對累積側向位移影響很小.