微下擊暴流風場模型在彈道仿真中的應用

陳健偉,王良明,李子杰,王 琦

(1.南京理工大學 能源與動力工程學院,江蘇 南京 210094;2.北京遙感設備研究所,北京 100854)

相關研究表明,氣象因素在影響火炮射擊精度的所有因素中占70%以上[1-2],其中,風是影響彈箭飛行的最主要氣象因素,因此,風對彈箭飛行的影響一直是彈道學中的研究熱點之一。文獻[3-4]基于隨機風場的統計特性,建立了空間簡化風速模型;文獻[5]基于火箭探空數據和熱成風公式,建立了100 km以內大氣風場分布模型,并分析了高空風場對遠程彈箭彈道的影響;文獻[6-7]根據外彈道氣象學理論,分析了幾種不同類型風場對彈丸彈道特性的影響,可以看出,目前對于彈道風場的建模主要以簡化平均風模型和隨機擾動風模型為主,并沒有考慮實際情況下常見的典型風場現象。

低空風切變是指海拔600 m高度內風速與風向的突變[8],其形成與天氣狀況、地形環境有著密切的關系。微下擊暴流是低空風切變的一種,其形成概率高、影響范圍大,當飛機彈箭在飛行過程中遭遇風切變時,突然變化的氣流速度和方向會改變其受力狀態,從而影響其飛行軌跡和穩定性[9-11]。目前,對于微下擊暴流風場的研究主要圍繞飛機展開,如飛行軌跡控制[12]、探測預警[13]等,而對于微下擊暴流對外彈道過程的影響鮮有研究。基于此,本文基于流體力學基本原理,建立微下擊暴流風場的非對稱多渦環模型,并與六自由度剛體彈道模型相結合,通過算例仿真,研究了微下擊暴流風場模型在彈道仿真中的應用,以期為惡劣氣候環境下的外彈道研究提供思路與參考。

1 微下擊暴流渦環模型

在空間范圍內,微下擊暴流通常表現為如下的流動形式:高度300～800 m范圍內,高壓氣旋(云層)中部形成一股向下的氣流,氣流撞擊地面后,呈輻射狀水平散開,并在外圍形成尾流旋渦,實景圖和示意圖分別如圖1和圖2所示。

圖1 微下擊暴流實景圖

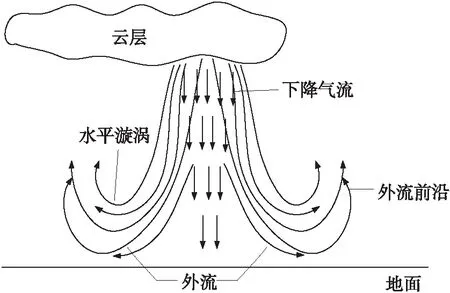
圖2 微下擊暴流形成示意圖

1.1 對稱渦環模型

在地面坐標系Oxyz中,以地面上方一點OP為中心設置主渦環,其半徑為R,如圖3所示,其在地面系內的曲線方程可表示為

(1)

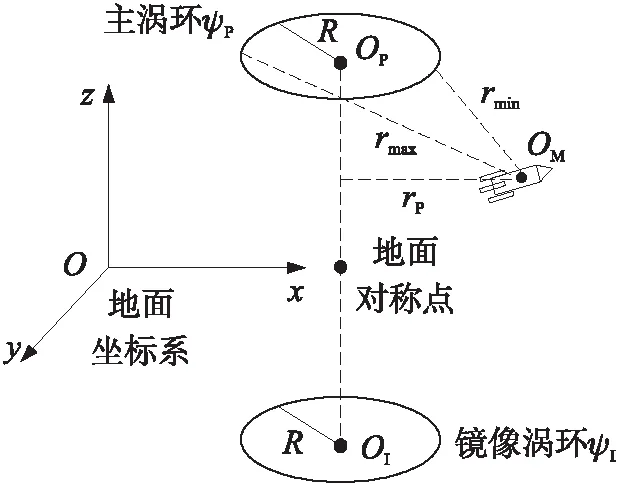
圖3 渦環設置示意圖

圖3中,下標P表示主渦環,I表示鏡像渦環。根據流體力學基本原理可知,主渦環流線方程為

(2)

式中:Γ為渦環強度,其大小取決于由渦環中心向下的誘導速度vz(0)及渦環半徑R。

Γ=2Rvz(0)

(3)

對于地面坐標系內的任意點OM(xM,yM,zM),rmax為該點到主渦環的最大距離,rmin為該點到主渦環的最小距離,F(k)為橢圓積分函數,有:

(4)

在0≤k≤1的情況下,F(k)有近似表達式:

(5)

通過對渦環流線方程進行偏導計算,可得到主渦環徑向誘導速度和軸向誘導速度:

(6)

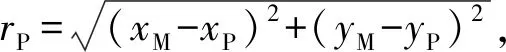
(7)

實際風場環境中,微下擊暴流中心向下的氣流撞擊地面向四周散開形成外流時,地面處的風速垂直分量應該為0,因此,通過設置一個與主渦環參數相同,位置與主渦環關于水平面對稱的鏡像渦環來滿足這一條件,鏡像渦環中心為OI(xP,yP,-zP),且有ψI=-ψP,因此,主渦環與鏡像渦環的誘導速度正好在水平面處相互抵消為0。通過與主渦環類似的計算方法,求得鏡像渦環在地面坐標系下的速度分量,最后,將兩渦環產生的誘導速度分量疊加,得到點OM處的合速度為

(8)

點OM的在地面系內的流線方程為

(9)

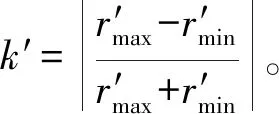
對于2種特殊情況:

①rP=0時,由流線方程計算出的誘導速度趨近正無窮,不合理,因此該點速度由渦環位函數偏導計算:

(10)

②渦環線上,rP=R,zM=zP處的點,以渦環線為中心,構造半徑為r的封閉環形圓柱,由于渦量在圓柱內均勻分布,因此圓柱內沿半徑方向誘導速度線性分布,如圖4所示。

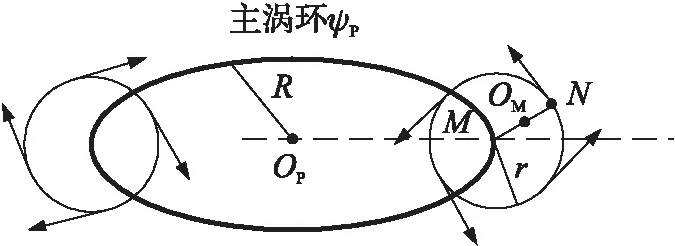
圖4 渦核內風速分布示意圖

當點OM位于環形圓柱內時,由渦環曲線方程聯立直線OPOM在水平面內的投影直線方程,可計算出點M的坐標和點N的坐標,而后根據點N的坐標,結合式(6)和式(7)即可獲得此時點OM處的風矢量。

1.2 傾斜渦環模型

實際情況下,微下擊暴流風場往往不是只由單個風暴中心(渦環)組成的,且水平輻射的外流也是非對稱的,甚至可能還存在上升氣流,因此,引入傾斜變換矩陣,通過多渦環疊加來模擬區域范圍內的微下擊暴流風場。

如圖5所示,令主渦環坐標系與地面坐標系的夾角向量為(φθ0)T,對應的旋轉矩陣為M(φ),則鏡像渦環與地面系夾角為(-φ-θ0)T,對應的旋轉矩陣為M(θ)。通過矩陣變換M(φ)M(θ)完成主渦環坐標系到地面坐標系的轉換,類似地,由矩陣變換M(-φ)M(-θ)實現鏡像渦環坐標系到地面坐標系的轉換。其中:

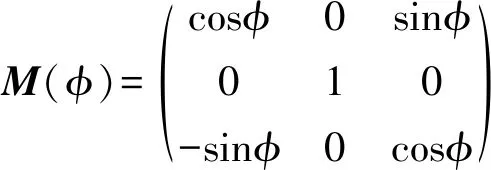
(11)

(12)

結合式(8),最終地面坐標系下三維風矢量為

(13)

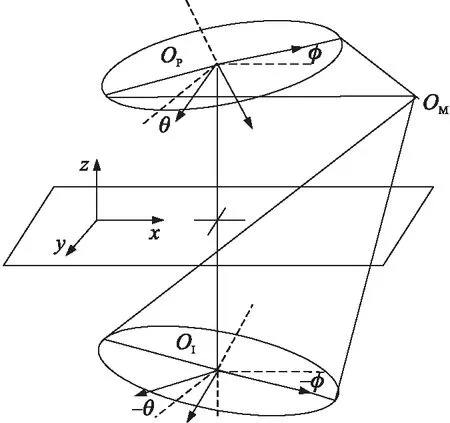
圖5 傾斜渦環示意圖

1.3 模型計算仿真

美國JAWS(聯合機場天氣計劃)美聯邦空管署FAA(federal aviation administration,FAA)的氣象研究資料[14]顯示,復雜微下擊暴流環境時,多風暴核在空間的位置分布間隔較為接近,且往往同時存在上升氣流中心和下沉氣流中心。參考文獻[15]的飛行仿真實驗數據,進行多渦環模型參數設置。

在地面坐標系一定區域內設定3個渦環,風場模型主要參數如表1所示,其中渦環1、渦環2為下沖氣流,渦環3為上升氣流;除渦環中心坐標外,渦環2和渦環3的其余模型參數同渦環1。表1中,P1,P2,P3分別為渦環1、渦環2、渦環3在地面系下的中心點。

表1 多渦環風場模型參數

圖6和圖7分別給出了微下擊暴流多渦環模型計算得到的水平截面和垂直截面內風矢量分布情況。由圖6可以看出,氣流在每個渦環的中心位置向四周呈輻射狀流動,風速沿徑向逐漸衰減;由圖7可以看出,渦環中心附近的下沖氣流具有較高的風速,氣流運動較為復雜,且由于非對稱傾斜角的存在,風速向一側偏移,到達地面后產生回流。

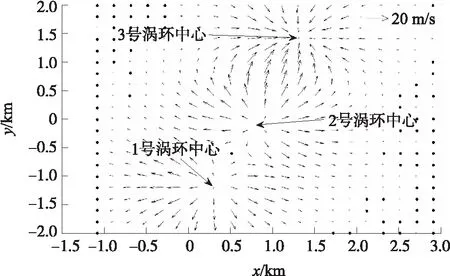
圖6 z=100 m時水平面風矢量分布

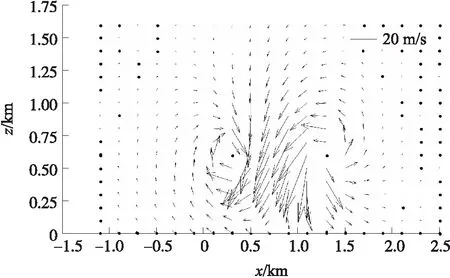
圖7 y=0時垂直面風矢量分布

綜合圖6和圖7可以看出,所建立的非對稱多渦環微下擊暴流風場模型具有良好的空間三維特性,能夠較為合理有效地描述實際微下擊暴流風場的風速分布特性。

2 計及風場的彈道模型

根據外彈道學理論[16],將運動中的火箭彈視為常質量的自由剛體進行受力分析,忽略火箭燃氣慣性作用力和力矩,同時不考慮發動機燃料燃燒對質心移動加速度以及轉動慣量的影響。通過聯立彈道坐標系及第一彈軸坐標系內火箭彈的質心運動和繞心運動方程,即可得到野戰火箭彈六自由度剛體彈道模型:

(14)

(15)

(16)

(17)

dm/dt=mb

(18)

式中:t為彈丸飛行時間;v為彈丸質心速度大小;m為彈丸質量;θ1和ψ2分別為彈丸速度高低角和速度方位角;Fx2、Fy2、Fz2為彈道坐標系下作用在彈丸質心的合力分量;X,Y,Z分別為彈丸在地面坐標系下的位置分量;ωξ、ωη、ωζ分別為彈丸轉動角速度在彈軸坐標系下的分量;Mξ、Mη、Mζ分別為彈丸所受合外力矩在彈軸坐標系下的分量;φa和φ2分別為彈軸高低角和彈軸方位角;JC和JA分別為彈丸極轉動慣量和赤道轉動慣量;γ為彈丸自轉角;mb為火箭發動機燃料質量燃燒速率,當獲得火箭彈彈體參數、發射條件、氣象條件后,通過數值積分算法可計算野戰火箭彈的完整彈道。考慮風的影響時,速度坐標系下作用在彈上的力可以表示為彈體相對速度的函數:

F2=f(v-ω2)

(19)

式中:ω2為速度坐標系內的風矢量,當獲得地面坐標系下風速分量時,可將該分量投影至速度坐標系進行彈道解算。

3 彈道仿真分析

基于外彈道學基本理論,將地面系下的三維風矢量計入六自由度剛體彈道模型進行計算,通過數值仿真來驗證風場模型計算效果。

3.1 仿真條件

以某122 mm口徑尾翼火箭彈為例,其彈體參數和發射條件如表2所示。表中,d為彈徑,l為彈長,v0為火箭彈發射初速,ε為射角,φ為射向。在主動段彈道計算時,認為發動機燃料質量勻速率減小,且轉動慣量和質心位置均相應隨時間勻速率變化。仿真中,除微下擊暴流風場參數外,其余氣象條件以炮兵標準氣象條件為準。以火箭彈發射位置為原點,射向為Ox軸建立地面坐標系,微下擊暴流渦環中心位置同表1。

表2 火箭彈彈體參數與發射條件

3.2 不同風場強度下的仿真結果

根據風切變的定義,風速大小是風切變強度的決定性因素。表3給出了JAWS的多普勒雷達測量統計結果和美軍飛行數據記錄器FDR提取的微下擊暴流風切變數據比較[14]。

由表3微下擊暴流風切變中心風速變化換算得,渦環中心處的風速變化范圍為7.8～27.2 m/s,因此,在該范圍內設置微下擊暴流多渦環模型的中心誘導風速分別為10 m/s,15 m/s,20 m/s,25 m/s,進行風場干擾下的彈道仿真,并與彈道無風情況下進行比較。表4給出了彈道特征參數的仿真結果,表中,vT為火箭彈末速度。圖8為三維彈道軌跡圖。圖9和圖10分別為不同中心誘導風速下火箭彈高低攻角δ1和方向攻角δ2隨時間的變化曲線。

表3 微下擊暴流風切變多普勒雷達觀測數據和FDR記錄數據比較

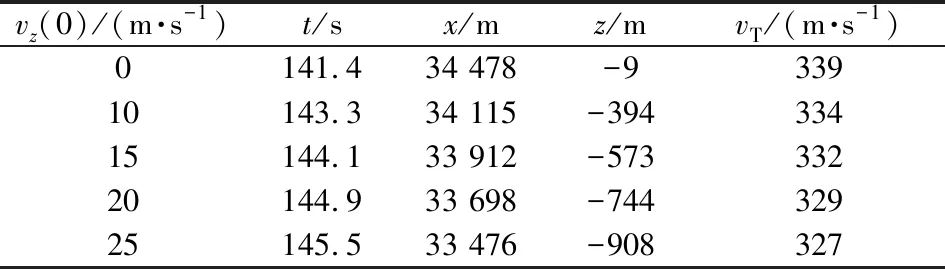
表4 彈道特征參數仿真結果

由表4和圖8可以看出,受到微下擊暴流風切變風場的影響,火箭彈的彈道特征量發生了較大變化,具體表現在:與無風情況下相比,火箭彈在空中飛行時間變長,落點側偏增大,射程減小,彈丸末速度降低;隨著渦環中心誘導風速的增加,相關彈道特征量的變化愈加明顯,可見風場強度是決定風切變對彈箭飛行過程影響程度的重要因素。

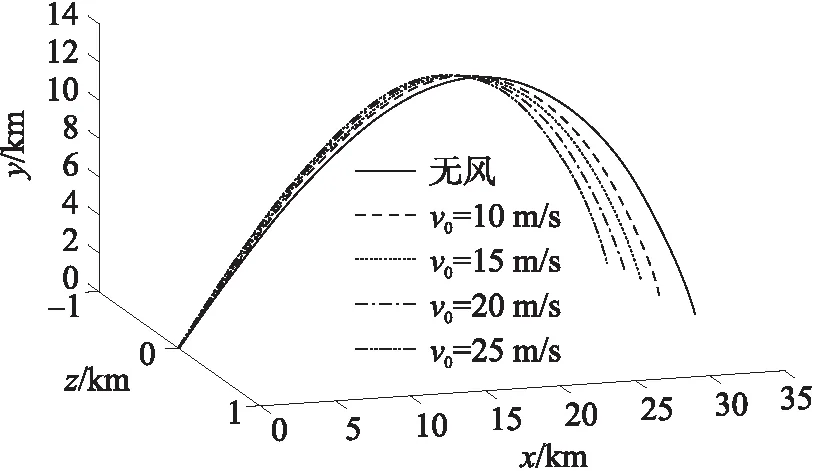
圖8 彈道軌跡圖

圖9 高低攻角曲線

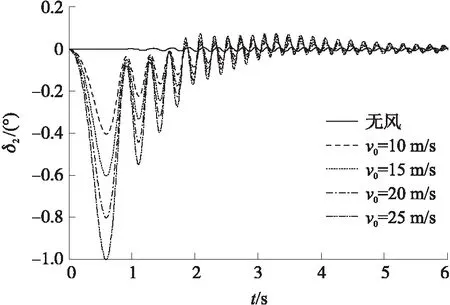
圖10 方向攻角曲線

由圖9和圖10可以看出,在主動段,尾翼火箭彈初速較低,抗擾動能力弱,當穿越氣流變化復雜的風場影響區時,高低攻角和方向攻角都發生了較大波動,高低方向的攻角波動出現了多個峰值,是因為受到了多個微下擊暴流渦環中心垂直氣流的影響。在推力作用下,火箭彈很快穿越高度幾百米范圍之內的風切變影響區域,而后在彈體靜穩定力矩作用下,攻角運動逐漸收斂趨于平衡。

4 結束語

基于渦環法建立了非對稱多核微下擊暴流風切變風場模型,通過彈道仿真計算,得到如下結論:①非對稱多渦環微下擊暴流風場模型具有良好的空間三維特性,能夠在一定程度上較好地描述微下擊暴流風切變的風場流動特征;②低初速彈箭(如部分火箭彈)在飛行過程中受到微下擊暴流風場干擾,飛行時間、末速度、落點位置和角運動過程均會發生變化,從而產生射擊精度偏差。如何探究風切變環境下彈箭飛行的控制方法,是后續進一步研究的內容。