引領學生“深度學習”的教學之道

陳華忠

【摘? ?要】深度學習是指在教師引領下，學生圍繞著具有挑戰性的問題，積極參與、主動探究、合作交流的學習過程。為此，教學中教師要引導學生去深度思考、深度體驗、深度交流與深度探究，體驗知識的形成過程，感受獲取成功的喜悅。

【關鍵詞】深度學習;教學之道;深度思考

《義務教育數學課程標準（2011年版）》指出：“作為促進學生全面發展教育的重要組成部分，數學教育既要使學生掌握現代生活和學習中所需要的數學知識與技能，更要發揮數學在培養人的思維能力和創新能力方面的不可替代的作用。”為此，教學應遵循數學學科特點、遵循學生成長規律，引導學生大膽猜測、深入思考，引領學生深度學習。

一、 以問題為驅動，打開深度思考之門

數學家哈爾莫斯說過：“問題是數學的心臟。”教學中，教師要以問題為導向，引導學生獨立思考、自主探究、合作交流，打開學生深度思考之門。例如，在教學“平行四邊形的面積”一課時，教師以“幫助工人計算草坪面積”為情境，提出：“這塊平行四邊形草坪的面積如何計算？”讓學生猜一猜，鼓勵學生思考不同的方法，并進行自主驗證，以“為什么平行四邊形面積等于底乘高”引導學生深入思考，促進學生自主探究。平行四邊形面積計算的教學，不僅要讓學生知道平行四邊形的面積如何計算，而且要讓學生知道為什么平行四邊形的面積等于底乘高。通過問題引領，學生對平行四邊形面積的計算公式的推導過程有了深刻的理解與思考，從而促進學生進行深度學習。

又如，在教學“三角形的分類”一課時，本課的主要問題是“分類的標準是什么”“為什么這樣分類”。教師引領學生通過操作、比較、觀察、感悟，發現三角形只要具有“共同的特征”就可以歸為一類。這樣就很清楚地解釋了為什么“一直二銳”與“一鈍二銳”不能合為一類，正是因為它們“共同的特征”不一樣，所以分成三類。

二、以互動為途徑，開展深度交流之話

交流互動的課堂最具魅力，教師在教學中應摒棄“師問生答”的傳統方式，更多地使用“生生互動”的方式，讓學生在交流互動中，相互啟發、相互碰撞，弄清問題的本質。

例如，在教學“9的乘法口訣”時，教師引導學生觀察算式并思考：“從上往下看，這些算式有什么變化？”“再從下往上看，這些算式又有什么變化？”“你發現了什么？”等。學生自由表達自己的想法，而教師可以根據學生的表達，發現學生思維的不足，及時地給予點撥引導，促進學生思維的發展。又如，教學“商不變的性質”時，學生經過觀察得出“被除數和除數同時擴大或同時縮小相同倍數，商不變”這一性質。此時，教師出示6÷3=（6×0）÷（2×0）=3讓學生判斷正誤。學生就能夠發現2×0=0，但是0不可以作為除數。可見，剛才得出的性質不夠準確、不夠完整，應該在條件中補充“擴大或縮小的倍數不能為0”。面對學生的發言，教師應該耐心等待，適時引導、辨析，直至學生深刻理解商不變的性質。

三、以活動為載體，做實深度體驗之功

數學的活動經驗需要在“做”的過程和“思考”的過程中積淀。只有讓學生親身體驗數學知識形成與發展的過程，才有真正的深度體驗。

例如，教學“涂色正方體表面積”時，教師首先展示了一個由27個小正方體拼成的涂色大正方體，然后讓學生打亂這個大正方體，看誰能花最短的時間還原。學生發現拼不出來后，教師問：“難在哪里？”學生說不知道哪個小正方體具體在什么位置。接著教師點撥引導，學生進行探究，發現了涂色正方體的特點，學生思維受到了啟發。教師又讓學生拼一拼由64 個、81個小正方體拼成的涂色大正方體，這一次有好幾組學生很快就拼出來了。教師打破以往觀察涂色正方體、尋找涂色規律的教學方式，把涂色的大正方體打亂，讓學生還原，培養了學生的空間觀念，提升了學生的數學素養。

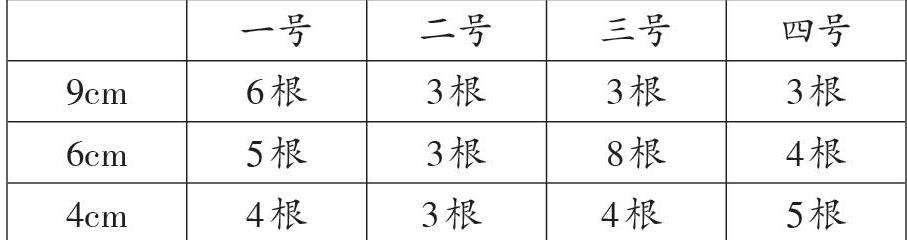
又如，教學“長方體的認識”時，教師組織學生小組內動手操作，并討論交流：第幾號材料可以搭出長方體框架？

小組成員相互探討，不斷嘗試，在實驗、分析、思考中發現：（1）如果是三組不同長度的小棒，每一組至少要有4根;（2）如果是兩組不同長度的小棒，有一組至少要有8根小棒，一組至少要有4根。學生深度參與，積極體驗，真正驗證了“自我發現的東西能積極地同化，從而產生深刻的理解”這一理念，深化了對長方體棱特征的認知，提升了學生的思維能力。

四、 以方法為手段，體驗深度探究之旅

深度學習不是一個接受知識的過程，而是發現、探究與創造的過程。如何引導學生自己去發現、去探究，體驗知識的形成過程，嘗到成功的愉悅呢？筆者認為，很重要的一點是多提供給學生自主探究的時間與空間，做到凡是學生自己能獨立思考的，教師絕不提示，凡是學生自己能探究的，教師絕不替代。例如，在教學“圓的認識”時，在“探索直徑和半徑的特點”這一環節，教師放手讓學生進行自主探究。

1.小組探究。以小組為單位，利用圓片，采用畫一畫、量一量、折一折等方法進行探索和研究：（1）半徑有多少條？直徑呢？（2）半徑有什么特征？直徑呢？（3）半徑與直徑之間的關系是怎樣的？

2.交流匯報。學生通過折、畫、量等實踐活動，發現圓半徑與直徑的特征、半徑與直徑的關系，從而體驗知識的探究過程，感受成功的喜悅。

參考文獻：

[1] 閻乃勝. 深度學習視野下的課堂情境[J]. 教育發展研究，2013（12）.

（福建省福清市岑兜中心小學? ?350313）