探究與正方形有關(guān)的線段之間的數(shù)量關(guān)系

正方形作為最特殊的四邊形之一，具有平行四邊形、矩形、菱形的所有性質(zhì)，因而，以正方形為背景的幾何綜合題層出不窮.在題目中可以求線段之間的數(shù)量關(guān)系、位置關(guān)系、線段的長度、角的度數(shù)等等，解題時需要特別明確正方形的性質(zhì)，善于動手操作、大膽猜想，聯(lián)想學(xué)過的幾何基本圖形，恰當(dāng)?shù)奶砑虞o助線，運(yùn)用幾何推理方可得出結(jié)論.1 與正方形有關(guān)的兩條線段的相等關(guān)系

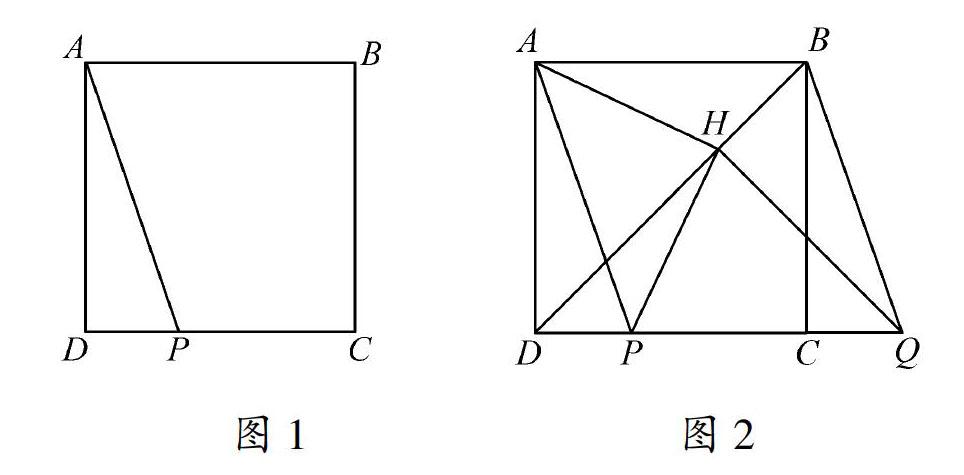
例1 如圖1，在正方形ABCD中，BD是一條對角線.點(diǎn)P在線段CD上（與點(diǎn)C，D不重合），連接AP，平移△ADP，使點(diǎn)D移動到點(diǎn)C，得到△BCQ，過點(diǎn)Q作QH⊥BD于點(diǎn)H，連接AH，PH.

1.依題意補(bǔ)全圖1;

2.判斷AH與PH的數(shù)量關(guān)系與位置關(guān)系

并加以證明;

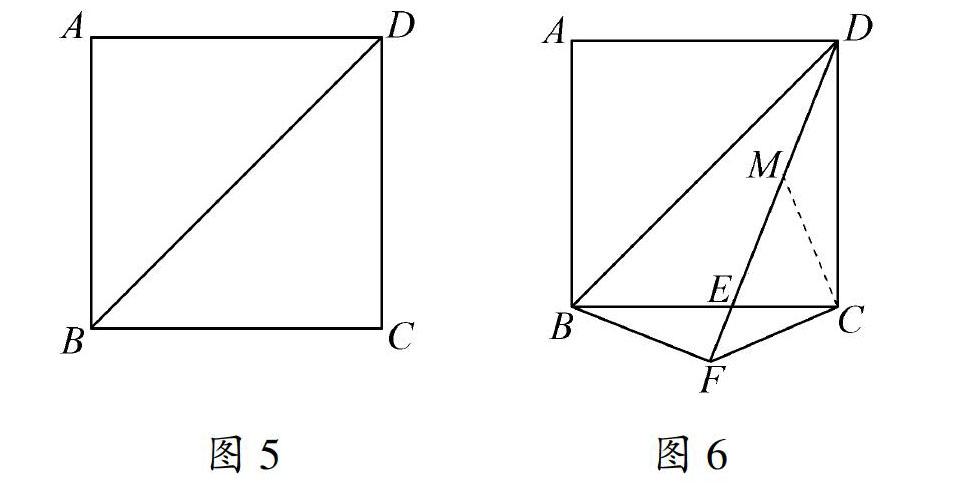
分析 1.依題意補(bǔ)全圖1，如圖2，主要關(guān)注：

（1）平移△ADP：平移的方向是沿著DC的方向，平移的距離是DC的長度;

（2）過點(diǎn)Q作QH⊥BD于點(diǎn)H：明確過點(diǎn)Q，作QH⊥BD于點(diǎn)H，垂足是H;

（3）連接AH，PH.

2.判斷AH與PH的數(shù)量關(guān)系與位置關(guān)系，這里包含兩層意思（1）AH和PH的數(shù)量關(guān)系，是相等還是不相等，還是幾倍的關(guān)系.（2）AH和PH的位置關(guān)系是平行還是垂直.本題解題時首先應(yīng)該利用刻度尺和量角器度量后進(jìn)行猜想，發(fā)現(xiàn)AH=PH，AH⊥PH.然后聯(lián)想學(xué)過證明線段相等的方法：三角形全等、等角對等邊、平行四邊形對邊相等.聯(lián)想證明垂直的方法：直角三角形兩銳角互余，矩形四個角為直角.結(jié)合本題條件，發(fā)現(xiàn)AH和PH所在的三角形，△HAD和△HPQ可以全等.因平移△ADP，使點(diǎn)D移動到點(diǎn)C得到△BCQ，知DC=PQ.由正方形ABCD

可得DA=DC=PQ，∠BDA=∠BDC=45°.QH⊥BD于點(diǎn)H，∠HDQ=∠HQD=∠BDA=45°，HQ=HD，所以△HAD≌△HPQ，HA=HP、∠AHD=∠PHQ.由∠DHP+∠PHQ=90°，所以，∠DHP+∠AHD=90°，∠AHP=90°，HA⊥HP.

反思 本題中正方形ABCD提供了以下重要條件：邊相等DA=DC、∠BDA=∠BDC=45°，

然后再充分利用其他條件進(jìn)行證明即可.2 與正方……