地震作用下雙槽渡槽半主動變阻尼控制分析

徐建國，王露安，崔軍豪，徐一鳴

(1.鄭州大學 水利科學與工程學院， 河南 鄭州 450001；2.中建八局華北公司， 河南 鄭州 450001)

由于半主動變阻尼控制在結構振動控制方面起到了很好效果，并在結構抗震減災中得到了不斷應用。半主動變阻尼控制裝置通過適時調整結構阻尼來消耗能量，達到降低結構關鍵部位地震響應的目的。由于僅僅需要調整液壓伺服閥的開口大小，故而所需的電能較少[1]，避免了主動控制所需要的高額定電壓、能量消耗過大等導致的對系統控制要求過高的缺陷。變阻尼控制屬于半主動控制，其控制力較容易實現，并且可以保證控制力出力大及在施加過程中的連續可變的特性。

Mohsen等[2]對半主動電磁摩擦阻尼器進行了全面的研究，并提出一種新的結構形式“SEMFD”。Gkatzogias等[3]通過對半主動控制技術在橋梁工程中的應用，提出一種基于性能的控制原則框架。Zhang等[4]提出一種新型AMD阻尼器件，以抑制不同地震激勵下的橋梁振動。Wang等[5]研究了一種振動控制策略，并進行了實驗驗證。林耿雄[6]以減震榫為例，研究了分離支座在橋梁結構振動控制中的優勢。董延東[7]通過對橋梁橫向振動控制的研究，證實了橋墩橫向剛度對結構振動有較大影響。黃永玖等[8]通過試驗研究，表明剪切式高阻尼橡膠減震器對拉索體系具有良好的減震效果。黃勁柏等[9]對高排架預應力混凝土渡槽建立了力學簡化模型，分析了三種抗震減震支座的渡槽上部結構自振周期、排架墩地震響應分析、上部結構地震位移響應和上部結構支座剪切變形響應，并對抗震減震效果進行了評價。潘崇仁[10]通過有限元軟件建立克孜河渡槽三維模型，模擬渡槽運行期溫度、應力分布規律。結果表明：運行期溫度應力較大，通過在渡槽外壁采取保溫措施，有效的改善了槽身的應力狀態。張威等[11]基于混凝土連續介質損傷力學和概率密度演化理論，結合物理隨機地震動建模方法和精細化有限元分析程序，建立了大型渡槽結構隨機動力反應分析與可靠度評估框架。汪權[12]針對地震作用下高層結構振動調諧質量阻尼器(TMD)被動控制問題，基于沿結構高度分布多個阻尼器的策略，研究分布式多重調諧質量阻尼器(DMTMD)控制策略并應用于高層結構振動控制中。鄔家利[13]拆解阻尼器觀察其內部變化情況，發現磁流變液泄漏或沉淀; 對阻尼器密封性能進行了實驗，得到了不同安裝角度的泄漏情況。張玉民[14]研究了渡槽結構伸縮縫兩端在地震中可能發生碰撞現象，危害渡槽的安全運營，甚至導致落梁破壞，針對這一問題，通過建立考慮碰撞效應的渡槽動力分析模型，研究了碰撞效應對渡槽地震反應的影響，并提出了對渡槽減震半主動控制方法。

鑒于半主動變阻尼裝置在實際工程減震防災領域的不斷應用，且由于其在大型渡槽結構振動控制的研究較少，故此開展大型雙槽渡槽地震響應振動控制研究很有必要。

1 雙槽渡槽半主動變阻尼控制分析模型

1.1 雙槽渡槽薄壁結構彈塑性動力分析模型

本文采用雙槽渡槽梁段單元非線性動力分析模型，計算渡槽結構橫向地震減震控制計算[15](雙槽渡槽截面示意圖見圖1)。雙槽渡槽截面尺寸較大，不能按照一般的開口薄壁梁來分析計算。通常做法是根據渡槽底板橫向連接較為薄弱的結構特點，在每個渡槽底板中點處假想斷開，將渡槽截面化為多個剛性橫截面(不計渡槽底板變形)的簡單薄壁梁(見圖2)，各自沿其形心C彎曲，并繞其扭心S扭轉。雙槽渡槽非線性模型集渡槽線彈性模型與非線性多彈簧模型為一體，并應用多彈簧等效關系模擬結構塑性鉸區的非線性滯回特性，充分考慮了截面混凝土、普通鋼筋和預應力鋼筋對非線性彈簧滯回曲線特征參數的影響，較全面準確地反映了結構的非線性動力性能。

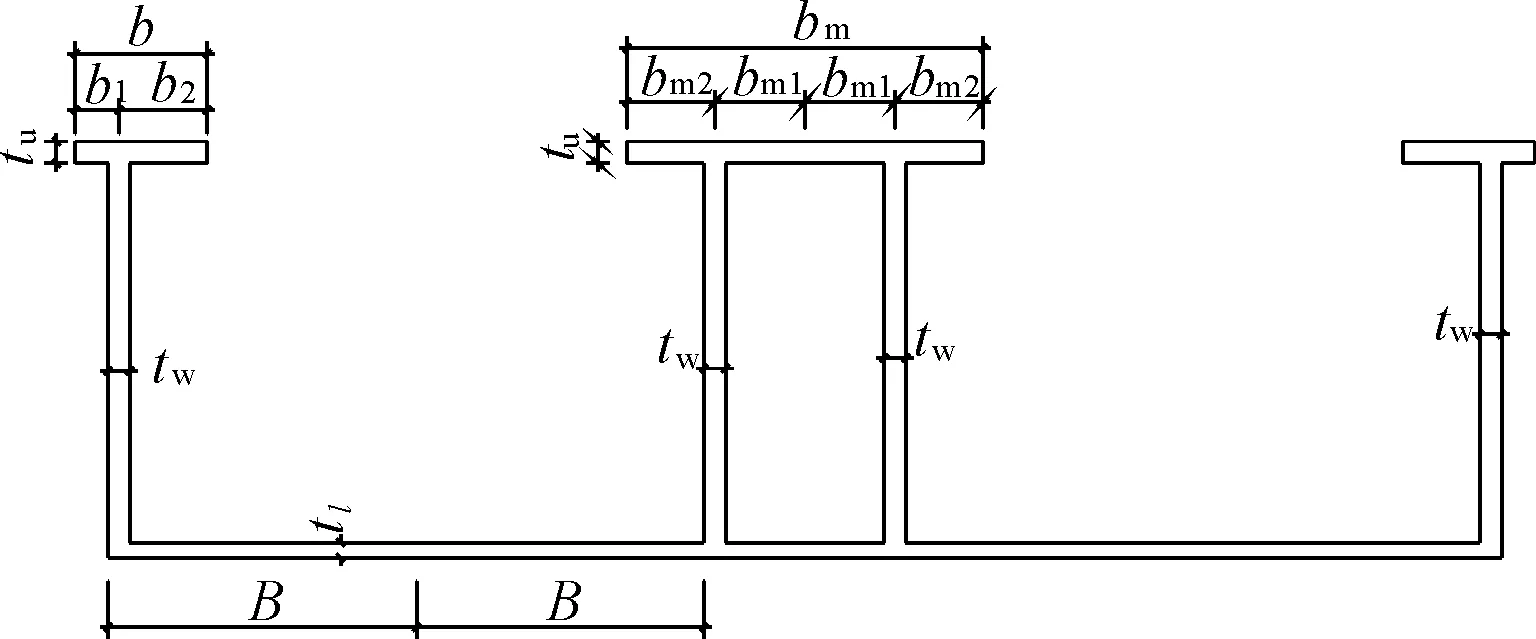
圖1 雙槽渡槽橫截面

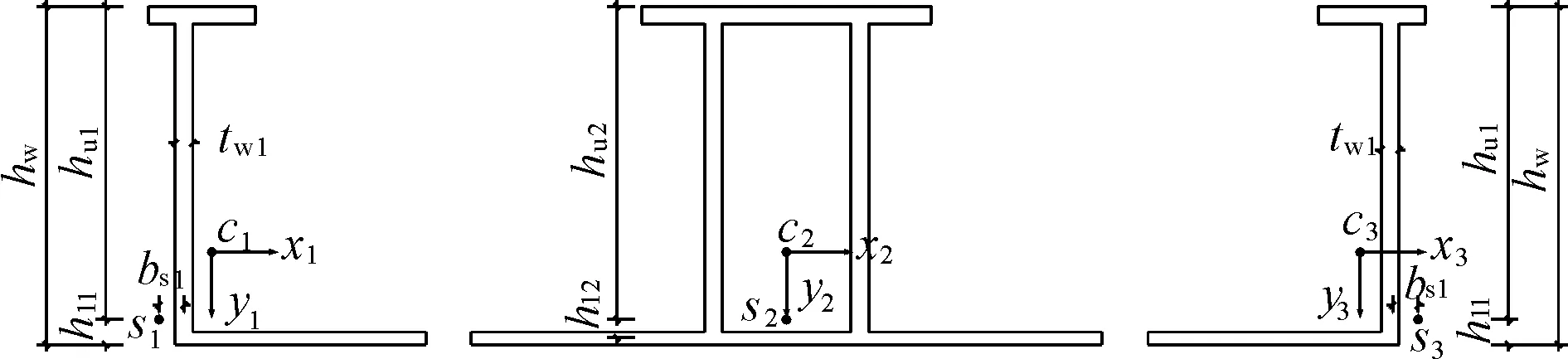
圖2 橫截面劃分示意圖

當渡槽截面在受到雙向彎矩發生彎曲變形時，則此時的截面彎曲變形的中性軸并不與截面慣性主軸平行，這就要求進行微元劃分和求解截面內力時必須沿主軸雙向劃分單元。應變計算時按照平截面假設，設某一位置處等效非線性彈簧內力和軸向變形可求為：

(1)

(2)

(3)

(4)

式中：Ps、δs分別表示某非線性彈簧的內力和單位長度的軸向變形；xs、ys為該非線性彈簧的位置坐標；φx、φy分別表示橫截面對x軸和y軸的轉動曲率[15]。

按照Guyan靜力凝聚的方法，將多彈簧彈塑性渡槽薄壁結構單元模型與渡槽彈性模型整理組合為一體。分別采用能量駐值原理和虛位移原理建立空間雙槽渡槽非線性動力分析模型(見圖3)[9]。

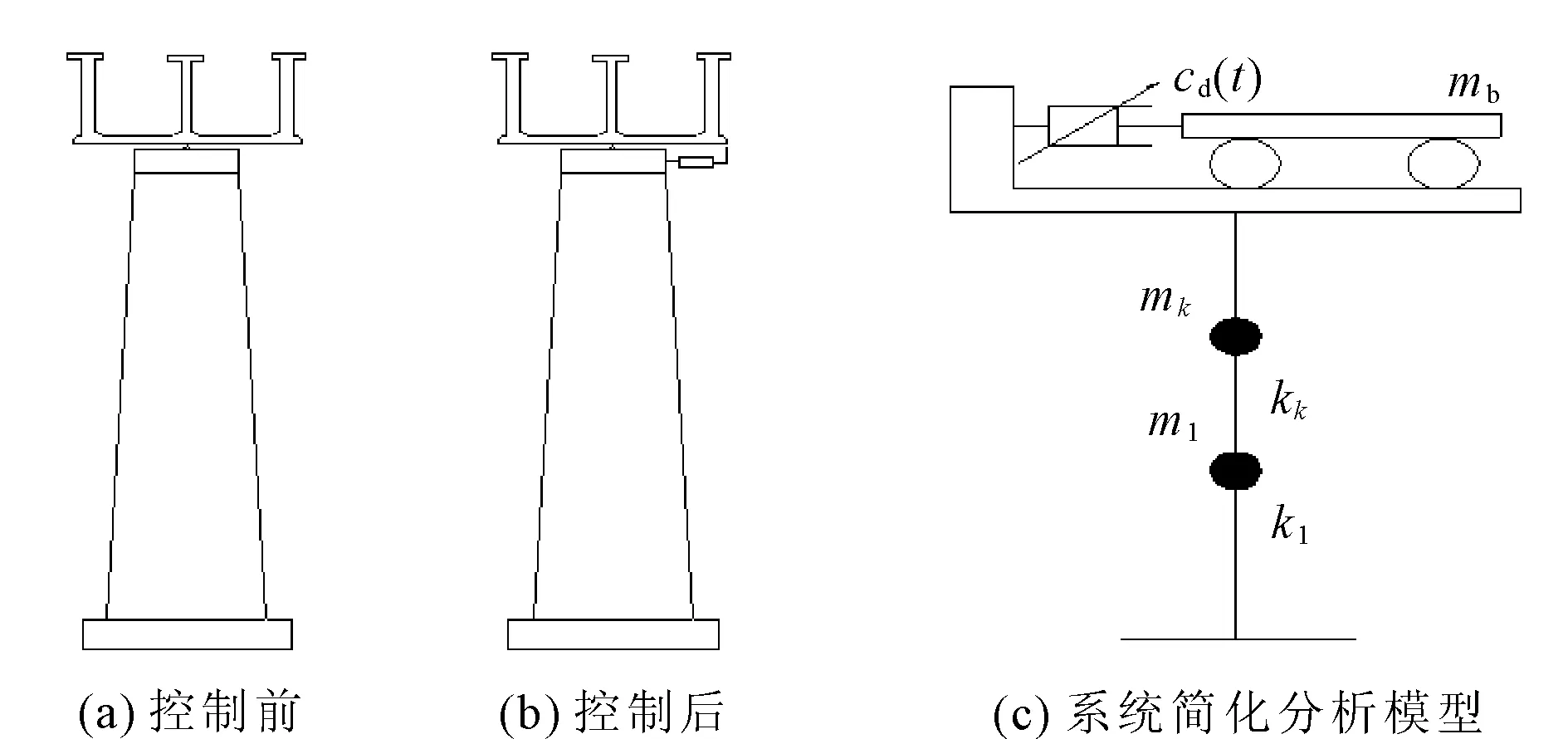
圖3 雙槽渡槽半主動結構控制系統

雙槽渡槽結構層間剪切模型在安裝變阻尼控制器裝置后的動力方程：

(5)

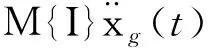
整體阻尼陣采用Rayleigh阻尼：

C=aM+bM

(6)

其中：

原方程經整理后得：

(7)

其中：

式中：mb為雙槽渡槽上部結構質量；kb為橡膠支座的水平剛度；cd(t)為阻尼器滯變系數。

1.2 變阻尼器控制原理

變阻尼控制器由調孔閥、液壓缸及輸油管線幾部分組成(見圖4)，當渡槽結構在地震荷載作用下產生動力響應時，測試系統自動檢測到結構響應參數，由處理系統計算出相應阻尼力大小，并反饋控制系統作為調節孔閥開口尺寸的依據，從而實現變阻尼控制實施。當調孔閥完全關閉時，提供的阻尼力最大；當旁路調孔閥完全打開時，阻尼力最小。通過控制器連續調整管路上孔徑的開口大小，使得阻尼器的阻尼系數在[Cdmin，Cdmax]區間連續變化，從而實現對變阻尼器的控制。

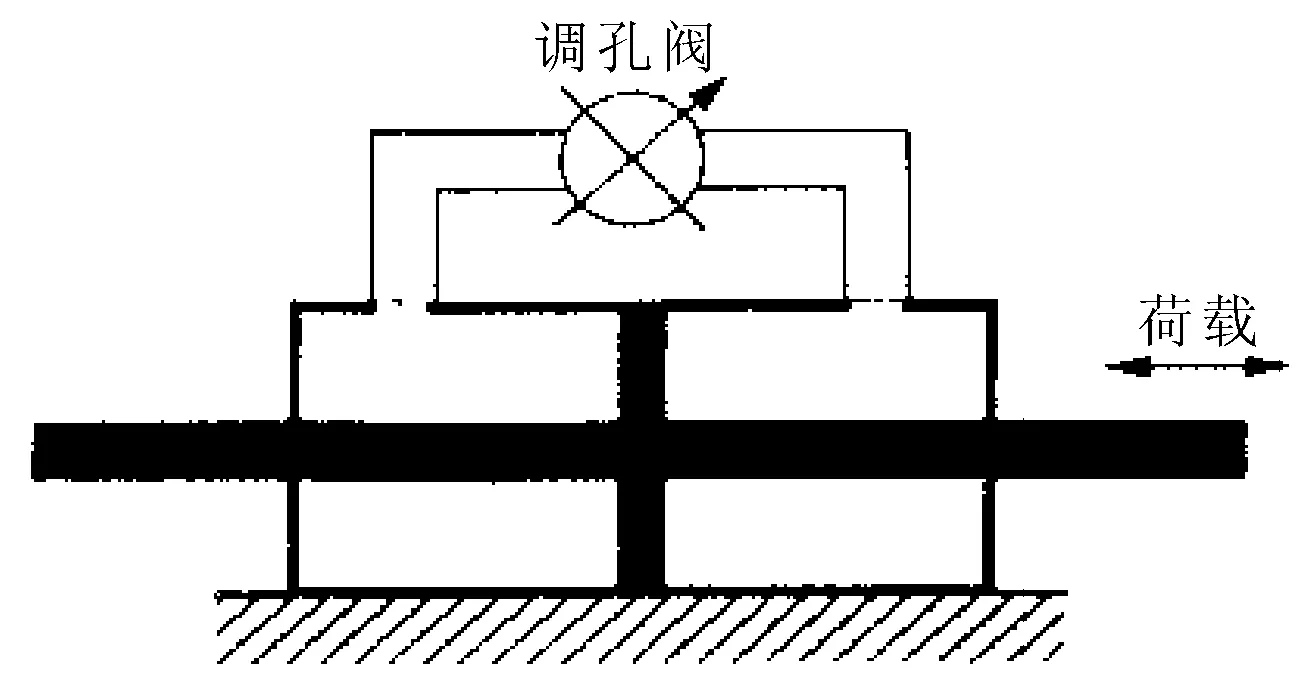
圖4 變阻尼作動器示意圖

1.3 控制裝置的計算模型

模型主要建立了阻尼控制器裝置中關于控制阻尼力、動力響應量和輸入電壓之間的函數關系。變阻尼作動器所提供的阻尼力由Maxwell模型確定：

(8)

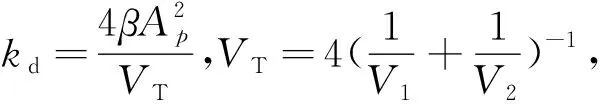
對于變阻尼控制器阻尼力計算模型，其它參數僅與變阻尼控制裝置的固有參數和缸內流體特性有關，只有阻尼系數cd可以通過控制調孔閥的開口大小調節，并且可以近似表示為：

cd=(1-λ)cdmin+λcdmax

(9)

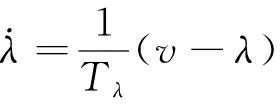
式中：cdmin和cdmax分別為變阻尼器所能提供的阻尼系數上下限值；λ為調孔閥開口控制參數，其取值范圍為0≤λ≤1，Tλ為時間常數，v為控制電壓。

2 主動控制力計算

(10)

Z(0)=0

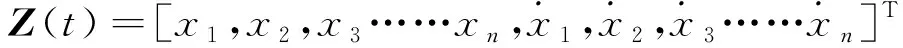
對于LQR算法，其性能指標定義為：

(11)

式中：tg為地震持續時間；Q2n×2n，Rp×p加權系數矩陣。

由式(4)、式(5)得到最小的主動控制力向量U(t)：

U(t)=-R-1BTPZ(t)

(12)

即：U(t)=-GZ，G稱為增益矩陣

P由下式求解得到：

-PA-ATP+PBR-1B-TP-Q=0

3 半主動變阻尼控制力計算

采用離復位控制算法為控制策略，即通過適時采集作動器瞬時速度，權衡控制力與結構運動關系來確定具體取值大小。根據控制阻尼力與可調控制阻尼之間的換算關系，采用限界Hrovat控制算法調整變阻尼控制力。

(13)

4 計算實例

雙洎河渡槽是南水北調中線總干渠最大的渡槽之一，渡槽全長240 m，單跨跨度40 m，全槽共分為1～6號跨，槽墩分為1～5號墩，在每個槽墩與槽身之間安裝有可變阻尼器，槽身為預應力鋼筋混凝土結構，渡槽與槽墩支墩的連接方式為簡支，雙槽槽身采用矩形單隔墻型式，槽身及墩體尺寸見圖5、圖6。槽身采用C50混凝土，槽墩采用C30混凝土，盆式橡膠支座彈簧水平向剛度為3.0×109N/m，槽墩底部采用鉆孔灌注樁基礎，現簡化為固定端約束模式。渡槽槽身和支墩均采用考慮塑性鉸的彈塑性梁段單元模型，該模型分為彈性梁段單元和非線性彈簧單元兩部分，其中非線性彈簧單元按照其非線性加卸載曲線分析計算。渡槽結構阻尼采用瑞利阻尼，阻尼比ζ為0.05，a=0.256，b=0.008；地震荷載采用調幅0.2g的El Centro、Taft和Tianjin地震波；可變阻尼器的阻尼系數cd(t)下限為989.60 kN·s/m，上限為54 889.30 kN·s/m。

從El Centro波減震控制效果來看(見圖7—圖16)，第1跨跨中位移主動與半主動控制效率分別為75%和40%；第2跨跨中位移主動與半主動控制效率分別為71%和39%；第3跨跨中位移主動與半主動控制效率分別為75%和40%；1號墩墩頂位移主動與半主動控制效率分別為75%和40%；2號墩墩頂位移主動與半主動控制效率分別為37%和7%；第1跨跨中加速度主動與半主動控制效率分別為36%和10%；第2跨跨中加速度主動與半主動控制效率分別為7%和4%；第3跨跨中加速度主動與半主動控制效率分別為36%和2%；1號墩墩頂加速度主動與半主動控制效率分別為10%和0.4%；2號墩墩頂加速度主動與半主動控制效率分別為10%和2%；3號墩墩頂加速度主動與半主動控制效率分別為23%和5%；3號墩半主動控制作動器最大出力占主動控制作動器的34%。

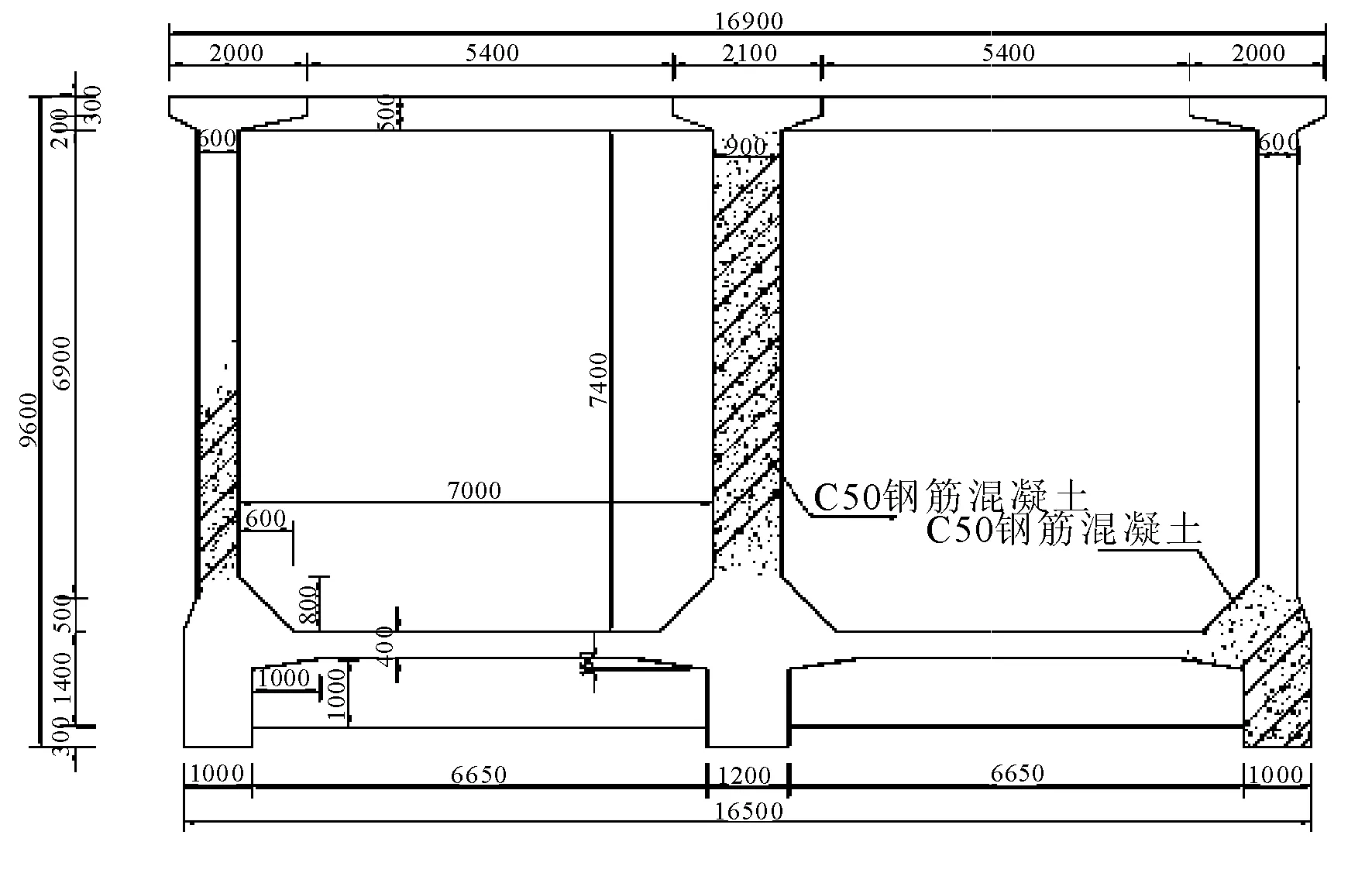
圖5 雙槽渡槽橫截面示意(單位：mm)

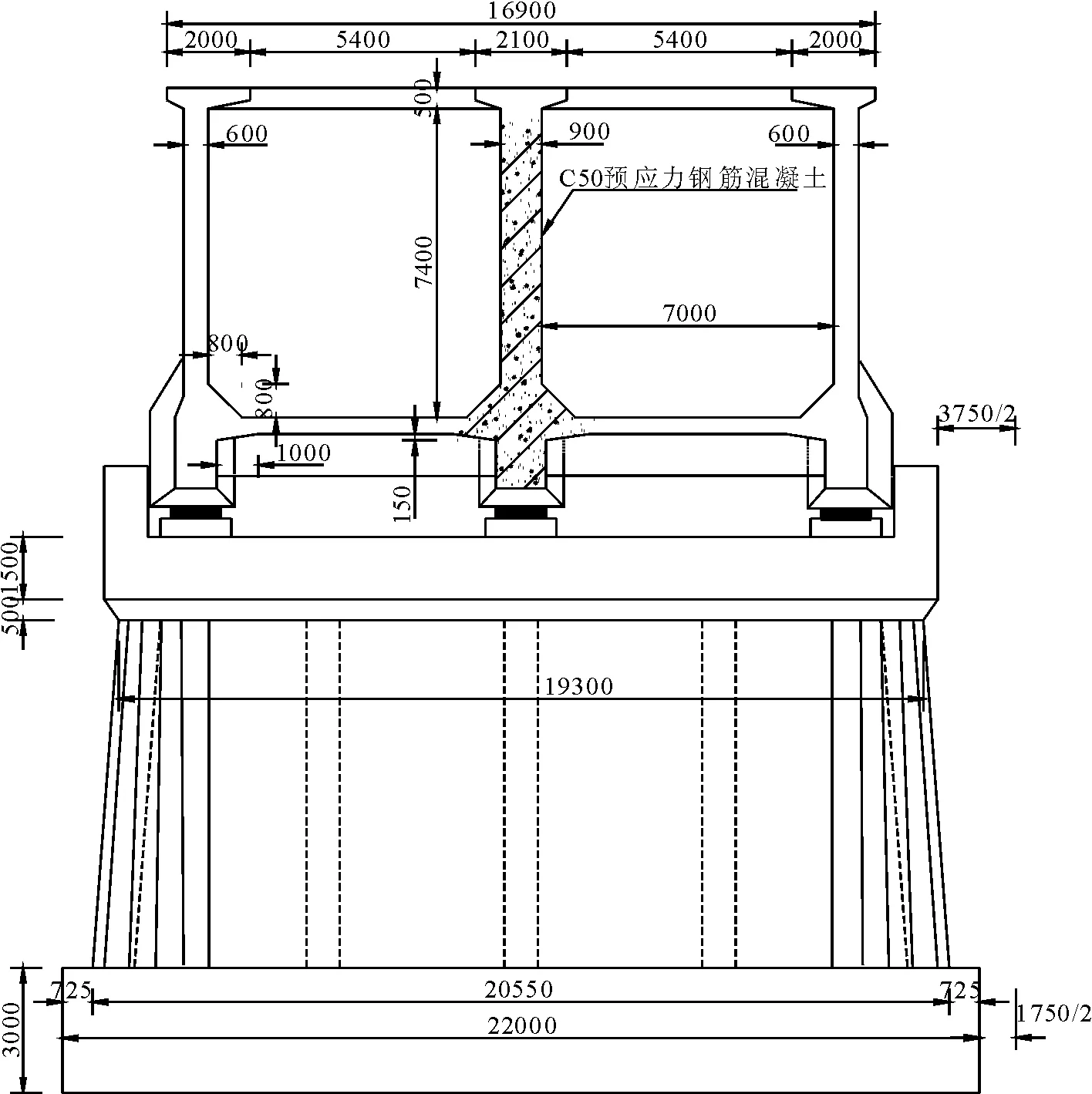
圖6 渡槽橫斷面及槽墩尺寸示意(單位：mm)

從Taft波減震控制效果來看(見圖17—圖20)，第1跨跨中位移主動與半主動控制效率分別為86%和52%；第2跨跨中位移主動與半主動控制效率分別為87%和52%；第3跨跨中位移主動與半主動控制效率分別為69%和48%；1號墩墩頂位移主動與半主動控制效率分別為75%和50%；2號墩墩頂位移主動與半主動控制效率分別為58%和17%；第1跨跨中加速度主動與半主動控制效率分別為61%和15%；第2跨跨中加速度主動與半主動控制效率分別為60%和10%；第3跨跨中加速度主動與半主動控制效率分別為61%和15%；1號墩墩頂加速度主動與半主動控制效率分別為47%和7%；2號墩墩頂加速度主動與半主動控制效率分別為10%和2%；3號墩墩頂加速度主動與半主動控制效率分別為15%和0.02%。

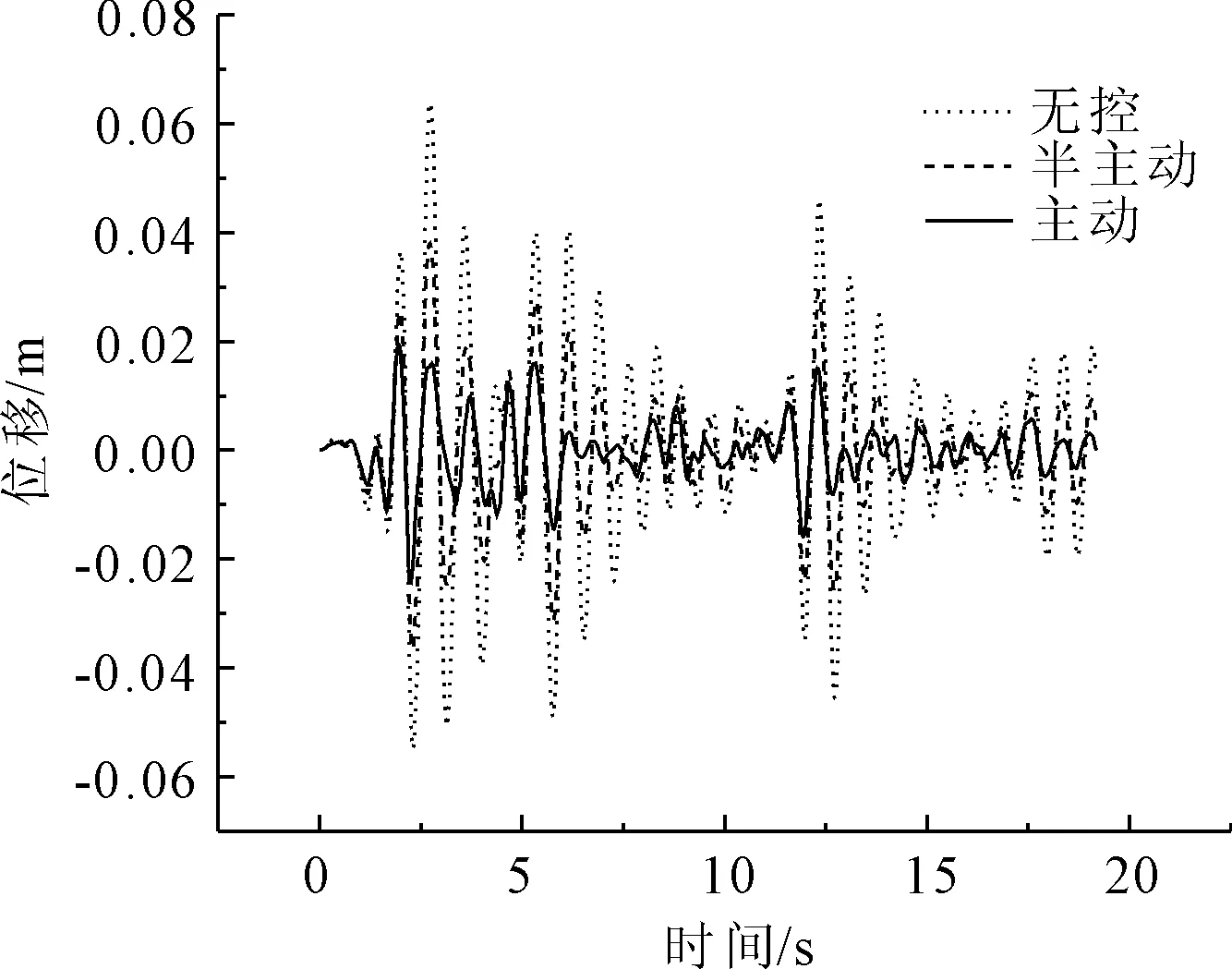
圖7 El Centro波第1跨跨中位移比較

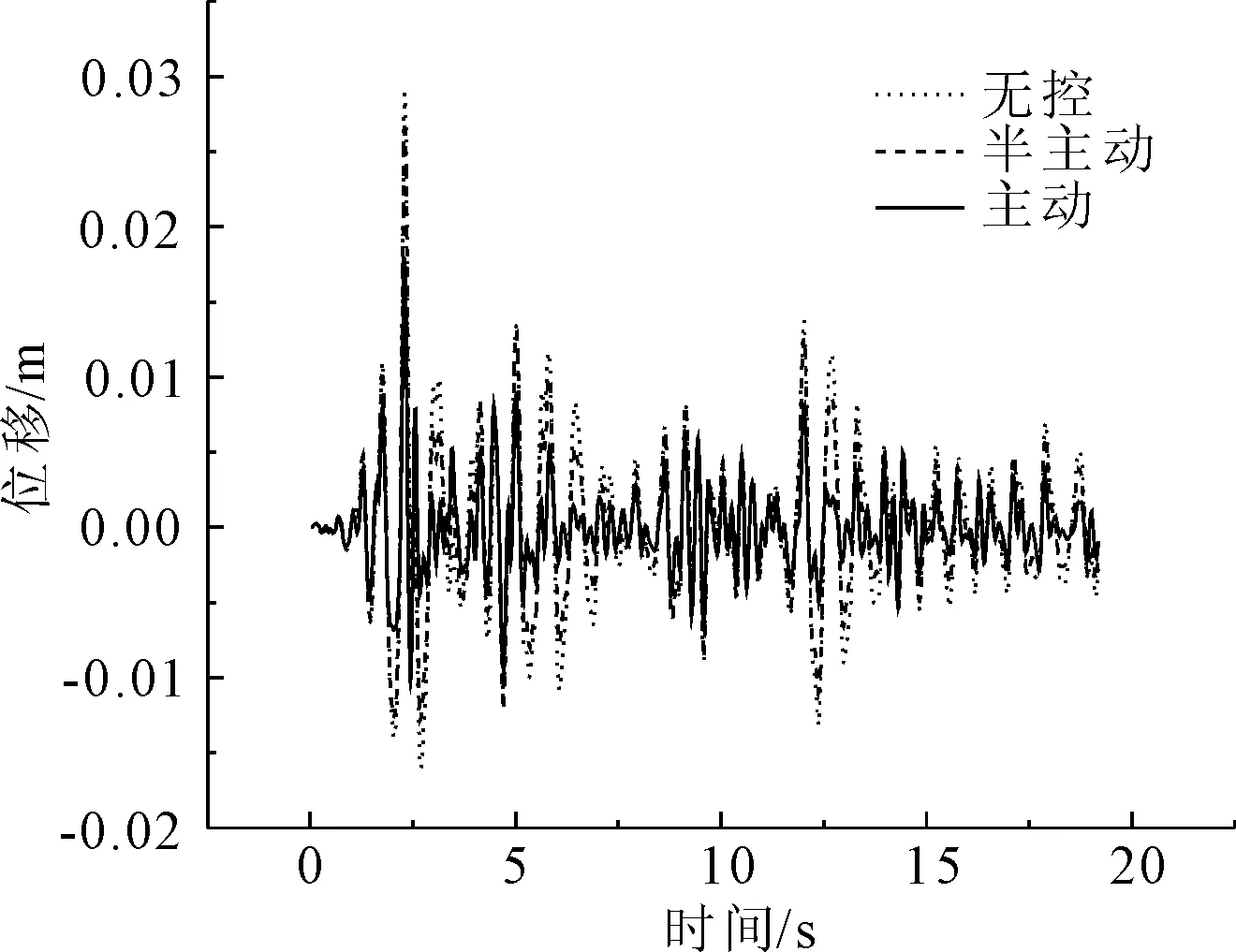
圖8 El Centro波第3跨跨中位移比較

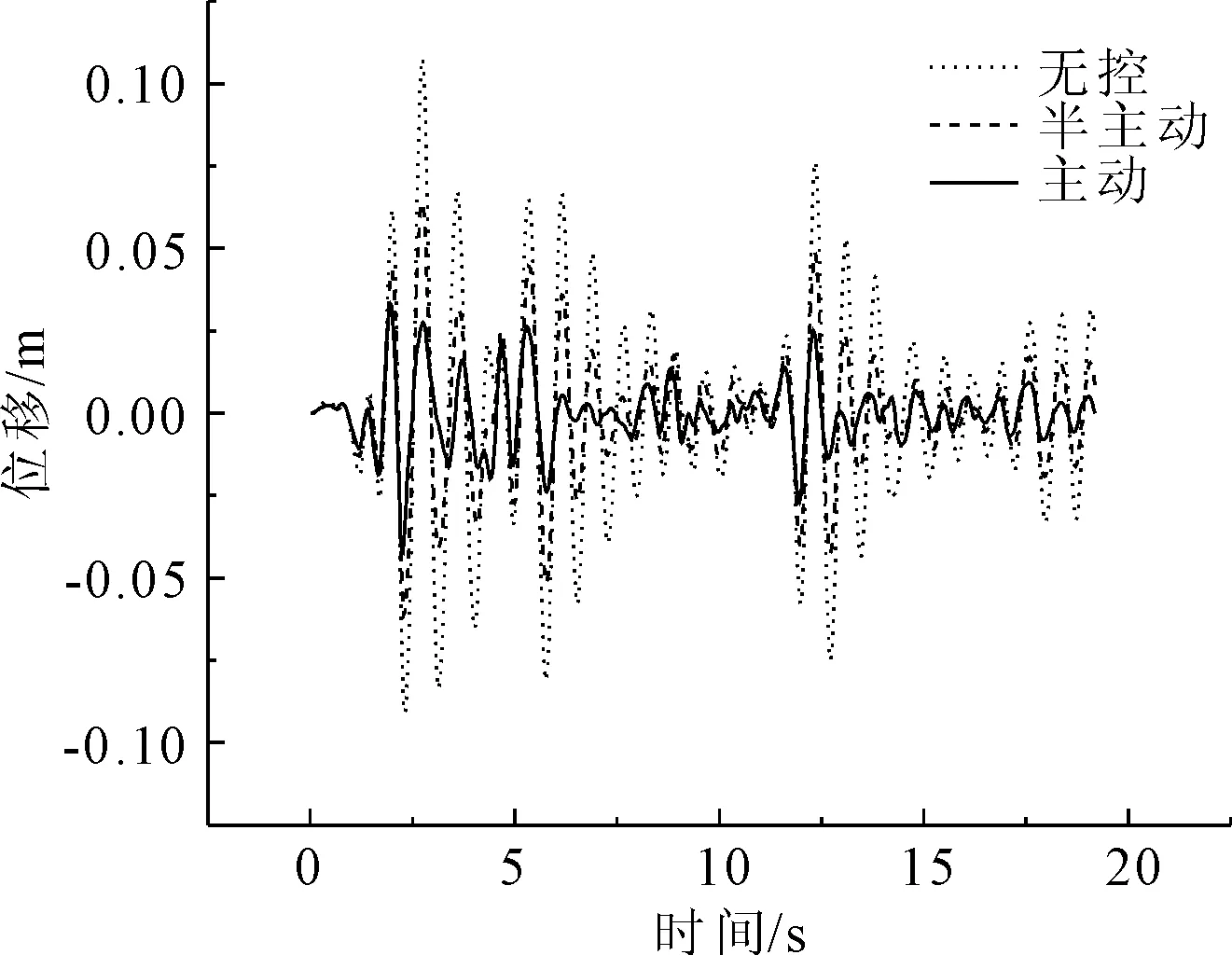
圖9 El Centro波2號墩頂位移比較

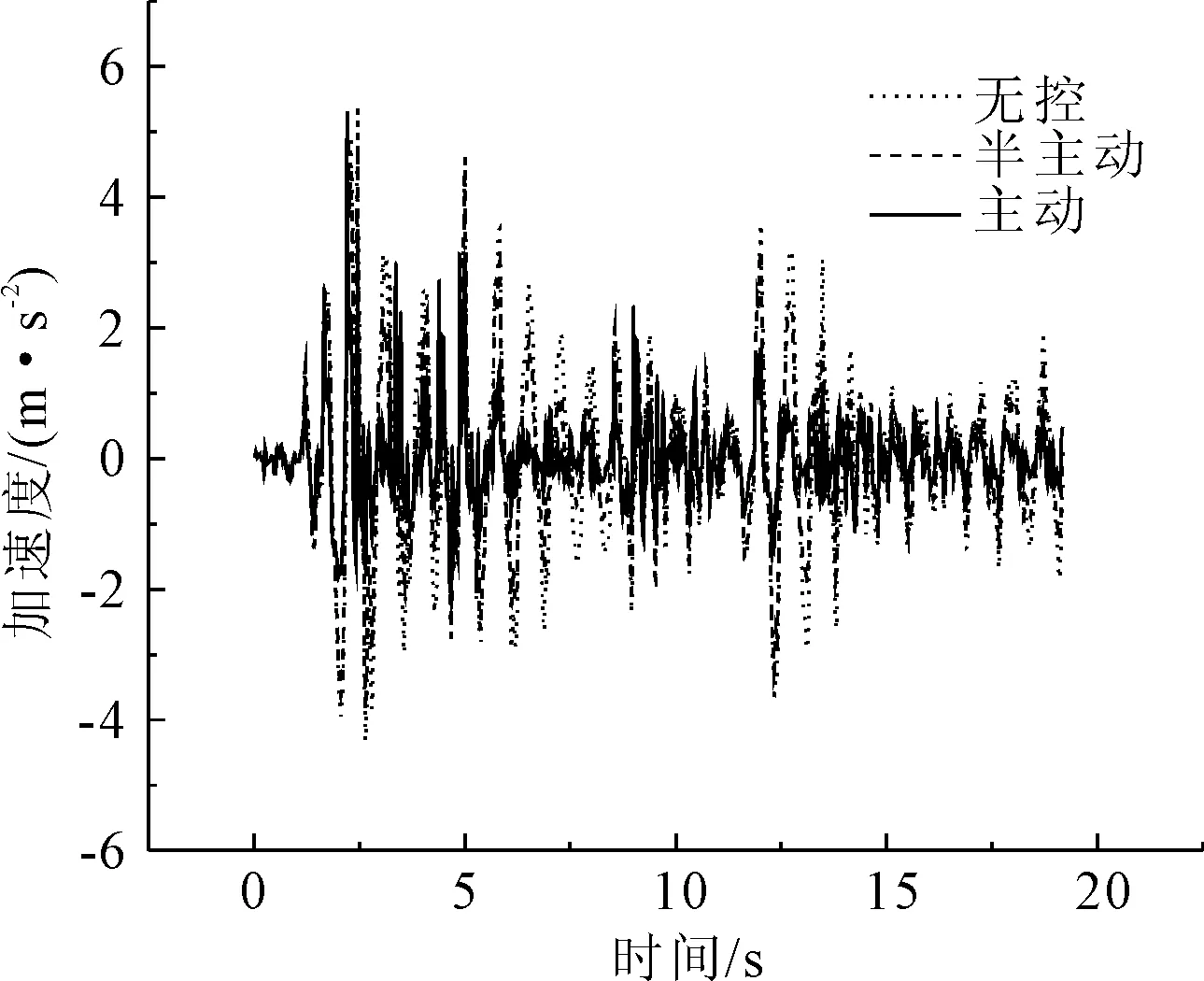
圖10 El Centro波第1跨跨中加速度比較

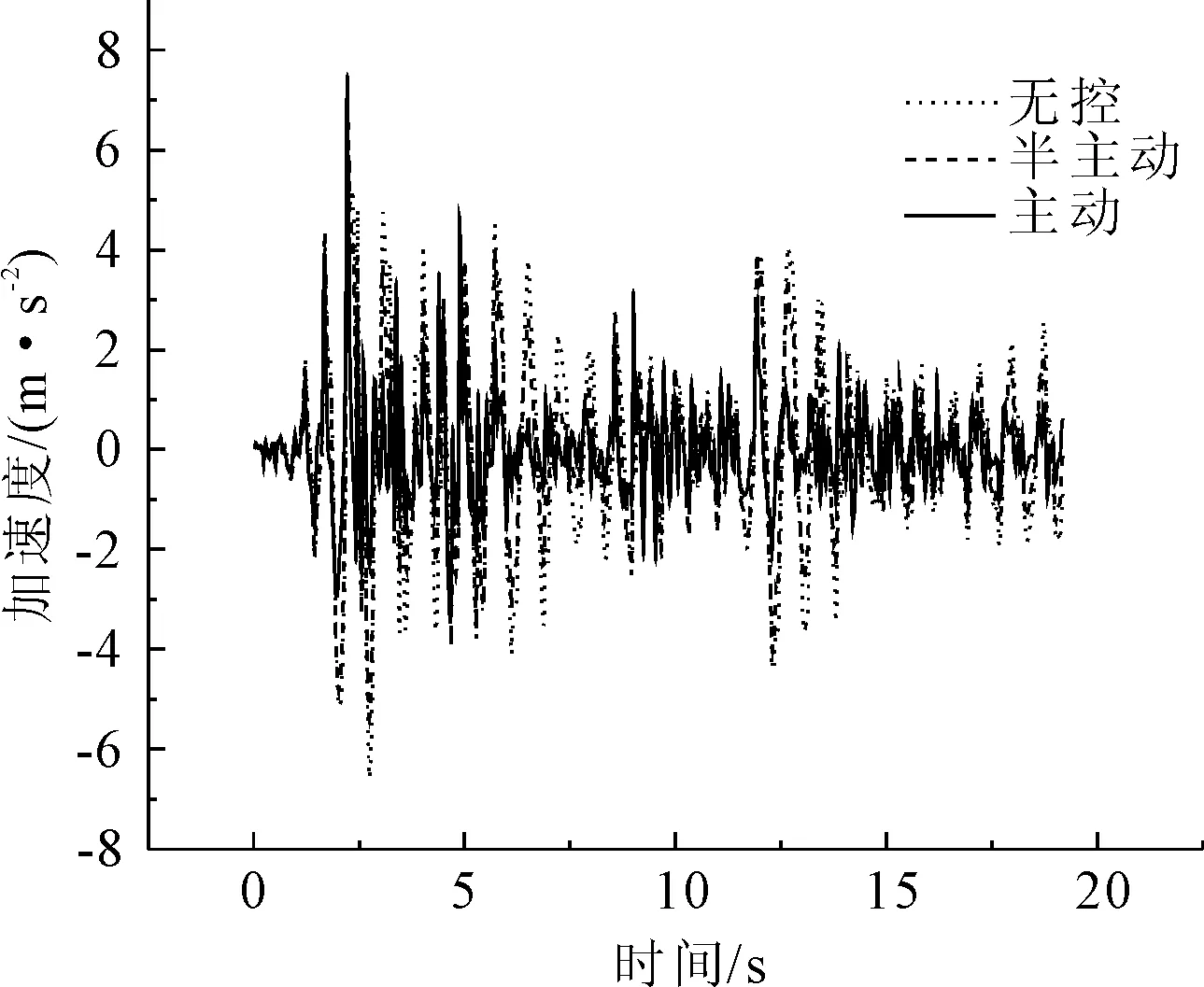
圖11 El Centro波第2跨跨中加速度比較

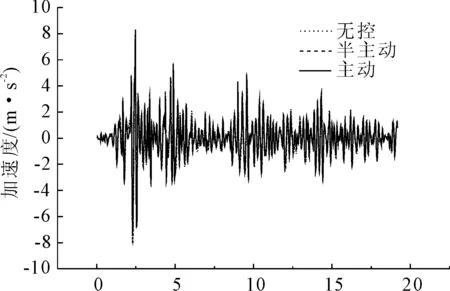
圖12 El Centro波第3跨跨中加速度比較

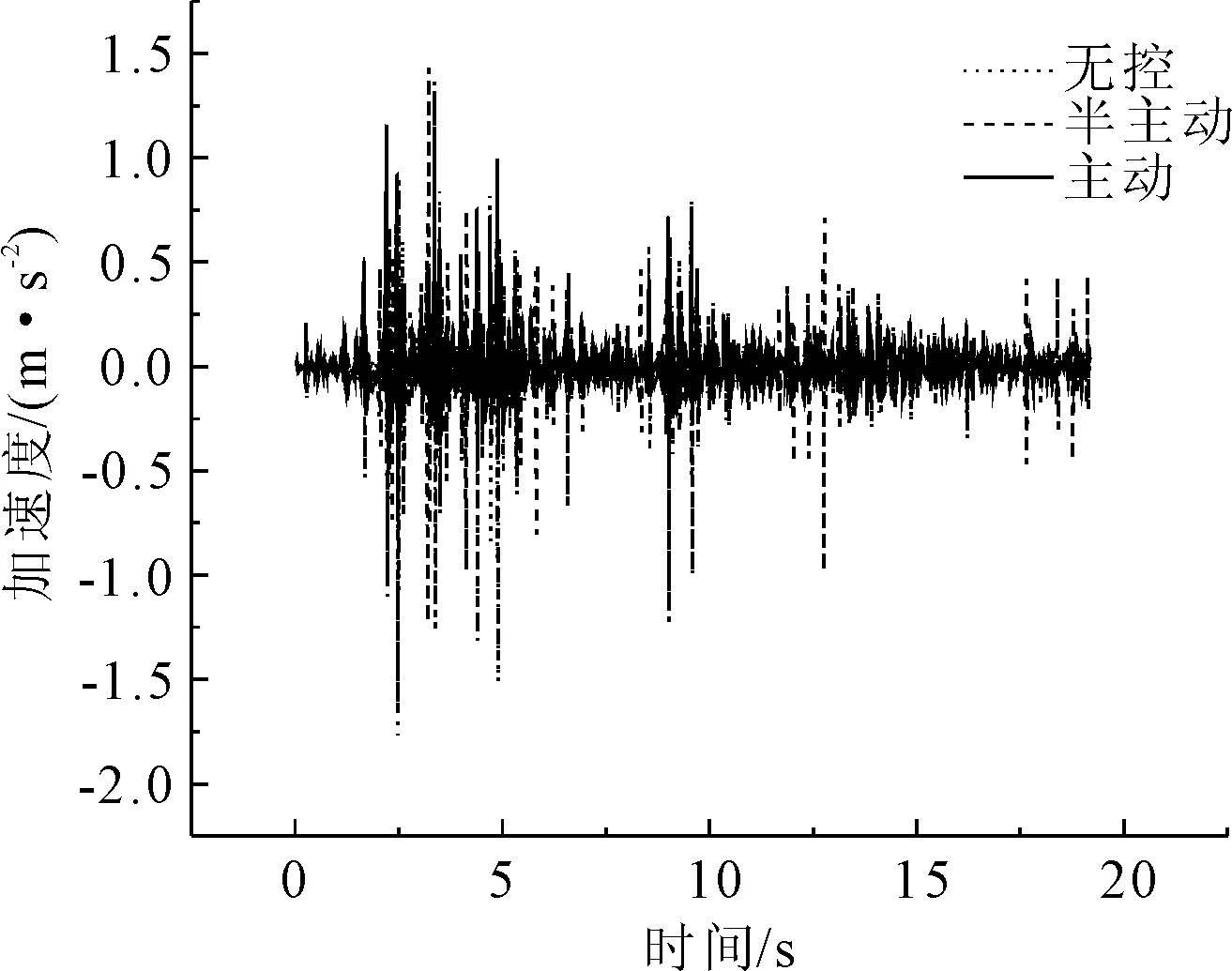
圖13 El Centro波1號墩頂加速度比較

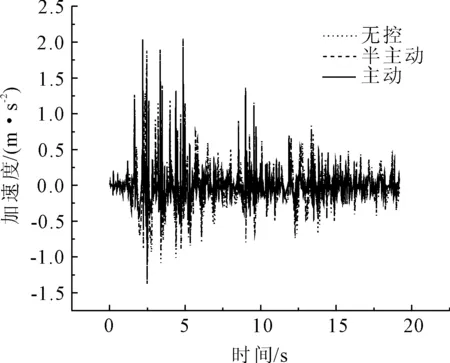
圖14 El Centro波2號墩頂加速度比較

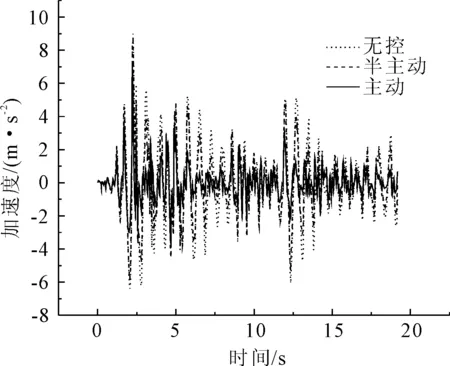
圖15 El Centro波3號墩頂加速度比較

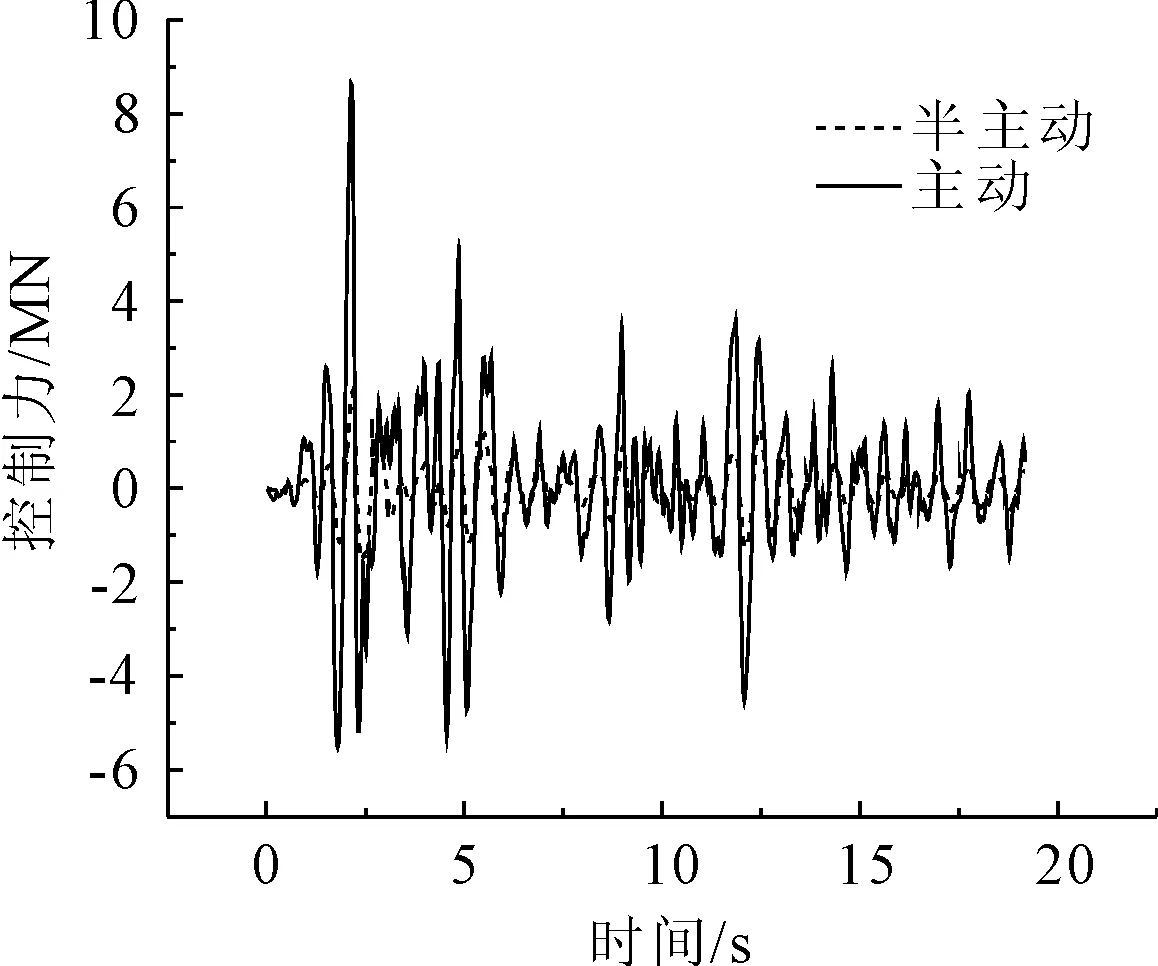
圖16 El Centro波3號墩控制器控制力比較

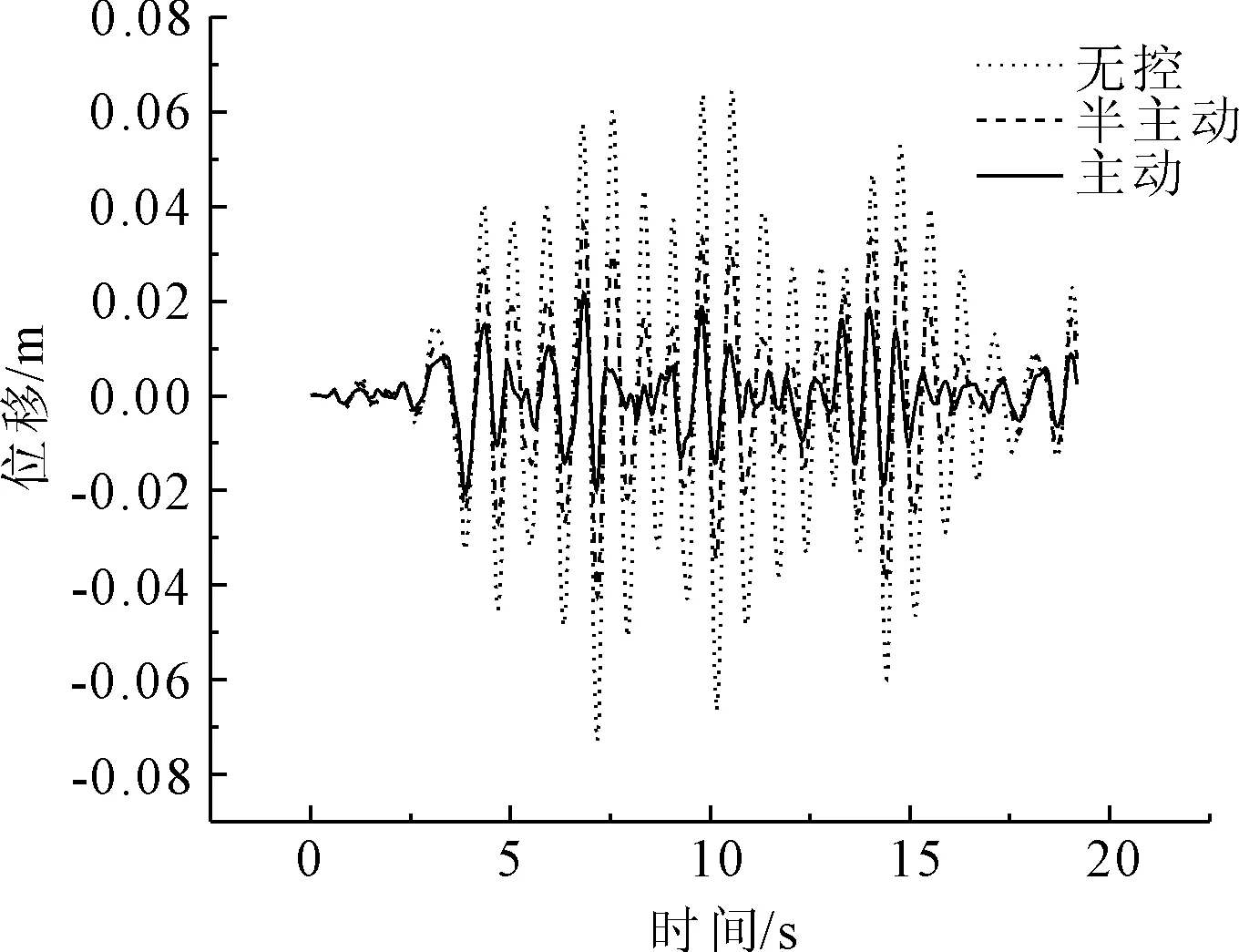
圖17 Taft波第1跨跨中位移比較

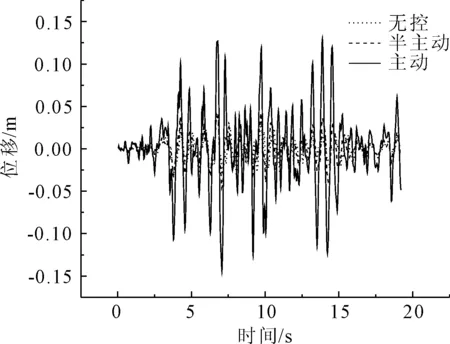
圖18 Taft波1號墩頂位移比較

從Tianjin波減震控制效果來看(見圖21—圖24)，第1跨跨中位移主動與半主動控制效率分別為70%和38%；第2跨跨中位移主動與半主動控制效率分別為67%和39%；第3跨跨中位移主動與半

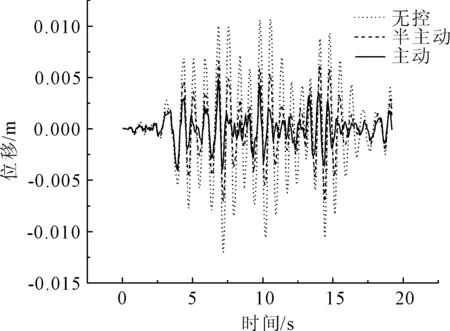
圖19 Taft波2號墩頂位移比較

圖20 Taft波第2跨跨中加速度比較

主動控制效率分別為70%和39%；1號墩墩頂位移主動與半主動控制效率分別為63%和50%；2號墩墩頂位移主動與半主動控制效率分別為63%和1%；第1跨跨中加速度主動與半主動控制效率分別為74%和24%；第2跨跨中加速度主動與半主動控制效率分別為67%和22%；第3跨跨中加速度主動與半主動控制效率分別為71%和23%；1號墩墩頂加速度主動與半主動控制效率分別為56%和18%；2號墩墩頂加速度主動與半主動控制效率分別為10%和4%；3號墩墩頂加速度主動與半主動控制效率分別為32%和11%；Taft波1號墩底彎矩值主動與半主動控制分別是無控墩底彎矩值的1.27倍和1.12倍；Tianjin波2號墩底剪力值主動與半主動控制分別是無控墩底剪力值的1.16倍和0.98倍。

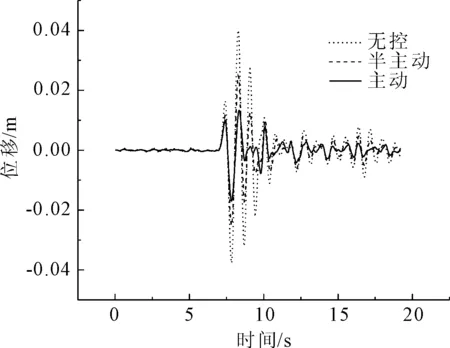
圖21 Tianjin波第1跨跨中位移比較

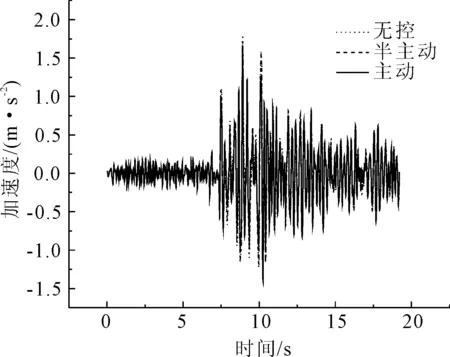
圖22 Tianjin波第3跨跨中加速度比較

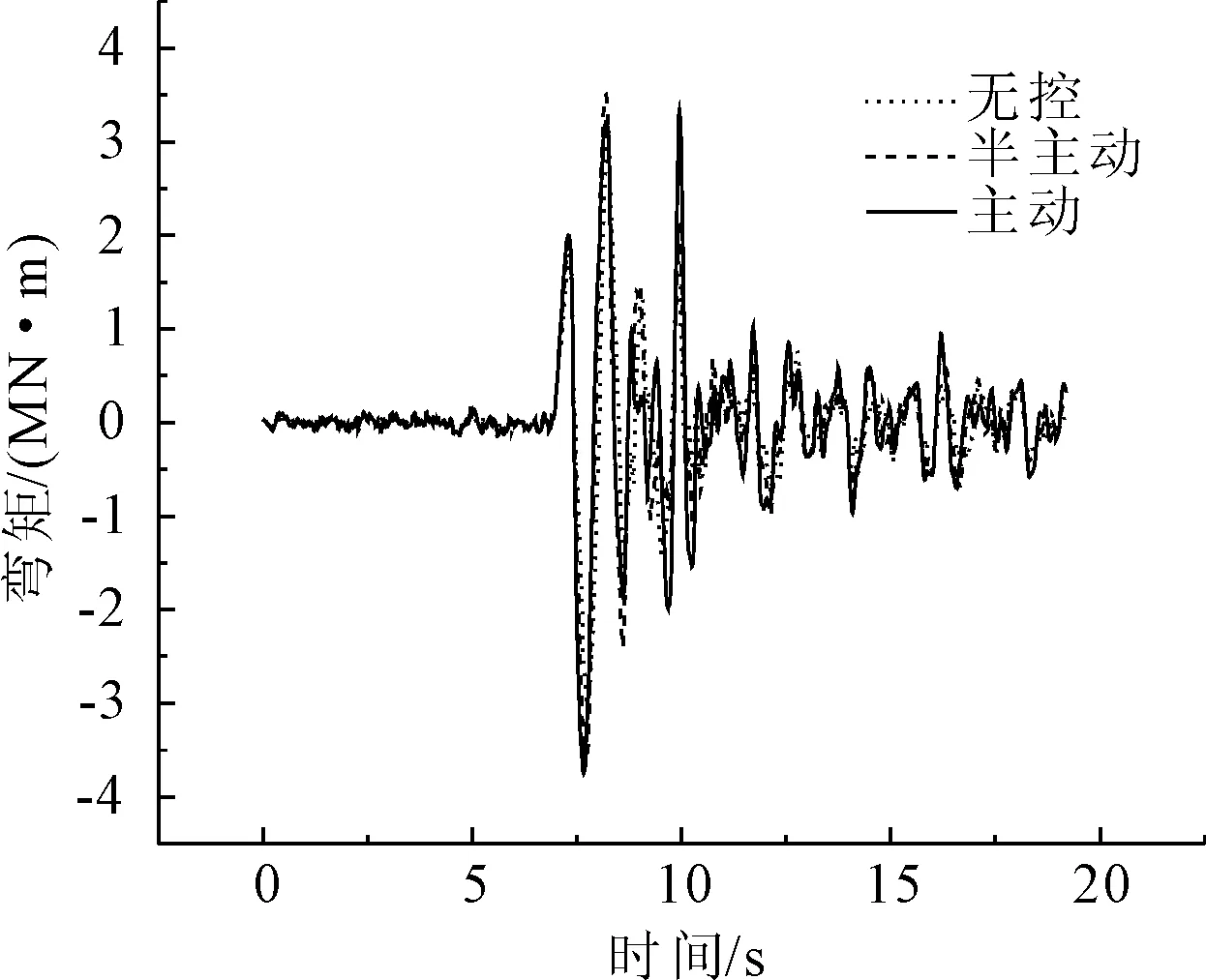
圖23 Tianjin波1號墩墩底彎矩比較

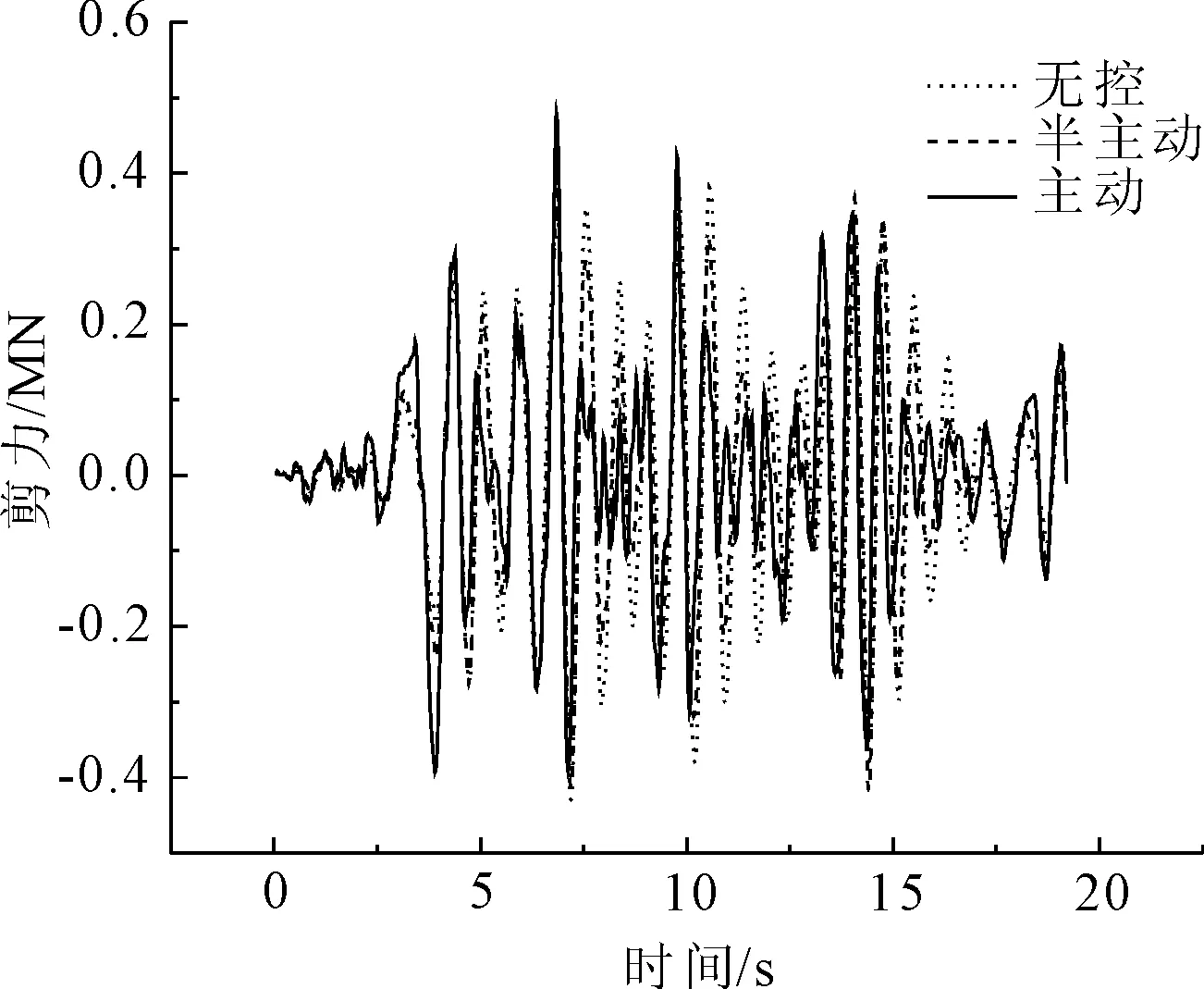
圖24 Taft波2號墩墩底剪力比較

從圖7—圖24地震時程響應曲線，以及表格1—表格3各條地震波下的地震響應對比結果可以看出，主動控制和半主動控制措施都明顯降低了各跨跨中橫向位移和橫向加速度最大值(如El Centro波第三跨跨中橫向位移：無控為0.108 m、半主動控制為0.064 m、主動控制為0.027 m；Taft波第二跨跨中橫向加速度：無控為8.476 m/s2、半主動控制為7.603 m/s2、主動控制為3.428 m/s2)；對比雙槽渡槽槽墩基底總剪力和總彎矩最大值，半主動控制內力較主動控制內力有明顯的降低(如Taft波1號墩底剪力：半主動控制為2.18×105N、主動控制為3.87×105N；Tianjin波1號墩底彎矩：半主動控制為3.42×106Nm、主動控制為3.85×106Nm)。同時也可以看到在半主動控制措施施加控制力后，在降低了結構位移反應的同時，部分槽墩墩頂加速度反應有所放大(如Tianjin波第三號墩頂加速度：無控為0.104 m/s2、半主動控制為0.115 m/s2、主動控制為0.071 m/s2)，墩底彎矩和剪力較無控時也增大明顯，這主要是由于控制力反向施加于槽墩頂部造成的影響。同時也可以看出，半主動變阻尼控制效果對關鍵部位的位移控制優于對加速度的控制；半主動變阻尼控制作為被動控制裝置，即使當外部大功率電源供電中斷時也可以保持較好的控制效果。

5 結 論

本文基于建立的雙槽渡槽結構動力分析模型，對比開展了三種不同控制工況下地震反應研究，主要包括結構無控、半主動控制和主動控制。計算分析了在三種場地條件地震波下的減震控制效果，最后得到如下的結論：

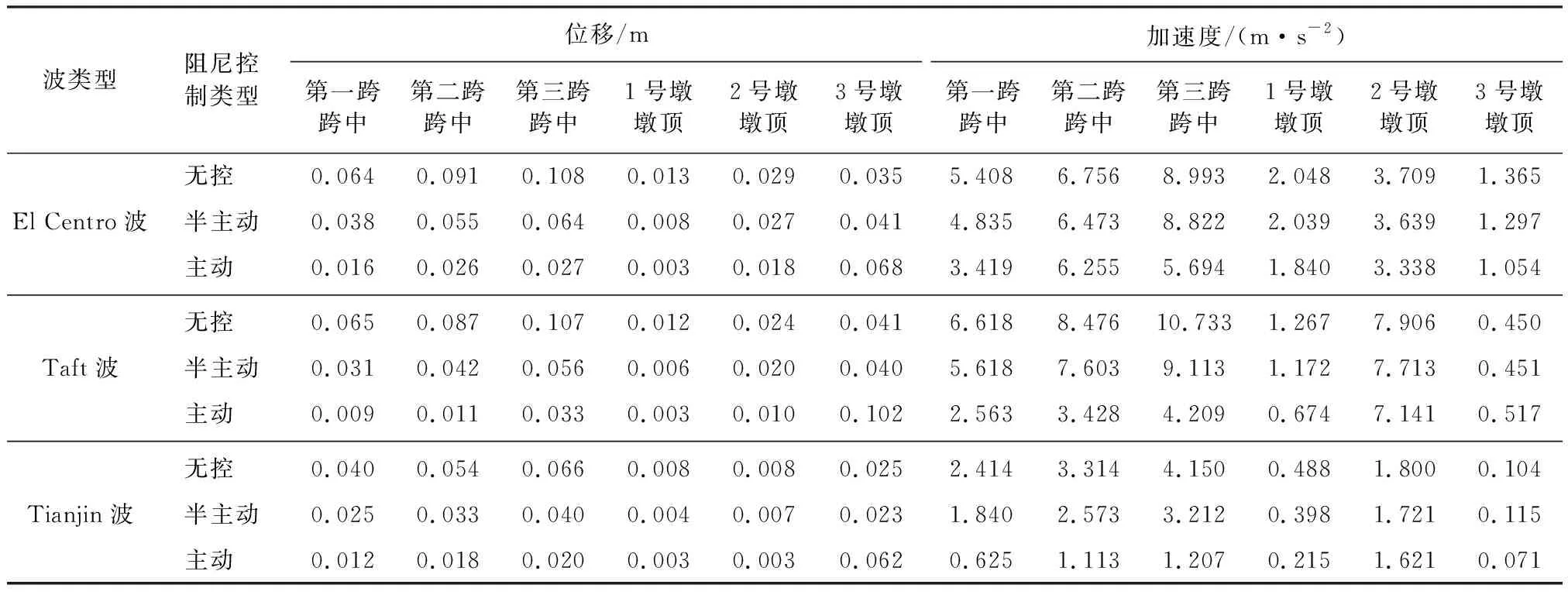
表1 雙槽在地震荷載作用下在最大響應參數

表2 三種地震波作用下墩底彎矩峰值比較

表3 三種地震波作用下墩底剪力峰值比較

(1) 以雙洎河大型雙槽渡槽為研究對象，充分考慮渡槽薄壁結構受力變形特性，按照Guyan靜力凝聚方法，分別采用能量駐值原理和虛位移原理建立了三維梁段單元雙槽渡槽非線性動力分析模型，并基于此模型進一步開展雙槽渡槽地震橫向振動控制研究。

(2) 采用主動控制和半主動控制均有效降低了雙槽渡槽各跨跨中的最大相對位移及跨中最大相對加速度；半主動控制較主動控制有效降低了各槽墩墩底彎矩以及墩底總剪力。

(3) 半主動控制在降低了結構位移反應的同時，部分墩頂的加速度反應有所放大，同時墩底剪力和彎矩較無控工況也有所增大，這主要是由于控制力反向施加于槽墩頂部造成的影響。同時也可以看出，半主動變阻尼控制效果對關鍵部位的位移控制優于對加速度的控制。

(4) 當發生高烈度強烈地震時，大型渡槽結構主動控制往往需要持續不斷的電力供應，這種持續電力要求若遇到供電中斷通常很難達到；而半主動變阻尼控制能夠在無電力供應情況下也能達到良好的減震控制效果，說明大型雙槽渡槽半主動變阻尼控制是一種適應能力較強的減震措施。