基于深度學習的小電流接地系統故障選線方法

張國棟，蒲海濤，劉凱

基于深度學習的小電流接地系統故障選線方法

張國棟1，蒲海濤1，劉凱2

（1．山東科技大學電氣信息系，山東省 濟南市 253500；2．洛陽供電公司，河南省 洛陽市 471000）

小電流接地系統的單相接地故障選線問題目前仍沒有完全解決。為了提高單相接地故障選線成功率，提出一種基于深度學習網絡的選線方法。首先，利用PSCAD搭建了中性點不接地系統仿真模型，通過設置每條線路在不同接地電阻下的故障，得到基于各出線零序電流幅值和相角的樣本數據，并將樣本數據分為訓練集、驗證集和測試集3部分。其次，基于Keras搭建了深度學習神經網絡，利用訓練集和驗證集數據對該網絡進行訓練。最后，利用測試集數據對訓練好的模型進行測試。結果表明，該方法具有建模簡單、成功率高及選線不受過渡電阻影響的特點。

小電流接地系統；單相接地故障；故障選線；深度學習

0 引言

我國10~35 kV配電網多為中性點不接地或中性點經消弧線圈接地的小電流接地系統[1-4]。小電流接地系統發生單相接地故障時，接地電流小，保護器無需跳閘，可以繼續運行1~2h，具有供電可靠性高的優點。由于故障電流小，在消弧線圈、故障點過渡電阻等因素的影響下，其故障選線問題仍未得到完全解決。

國內外學者對故障選線進行了大量研究。龍茹悅等[5]分析了特征頻段內的饋線零序阻抗性質，提出了針對諧振接地系統的故障選線新方法；方毅等[6]分析了諧振接地系統經高電阻接地時的暫態能量特征，并提出了相應選線方法；朱永利等[7]將S變換與混沌振子系統相結合進行故障選線；蔣凱等[8]利用高維隨機矩陣進行故障選線；文獻[9-11]將遺傳算法等優化算法與傳統BP神經網絡相結合，提高了選線正確率；徐銘銘等[12]提出了基于模型識別的諧振接地系統故障選線方法；沈興來等[13]將群體比幅比相法、五次諧波比相法、小波分析法綜合在一起，利用模糊理論判斷故障線路；劉謀海等[14]通過希爾伯特?黃變換(Hilbert-Huang transform，HHT)提取故障后零序電流高頻分量確定故障線路；陳奎等[15]建立了較為詳細的電弧模型，利用支持向量機進行故障選線；邵祥等[16]提出了基于改進動態時間彎曲(dynamic time warping，DTW)距離的接地故障波形互相關度聚類選線方法；魏鑫等[17]利用Hausdorff距離算法分析故障暫態零序電流差異程度，并進行故障選線。

以上研究所采用的選線方法可分為兩大類：1）采用各種數學變換提取故障電流的暫態分量或穩態分量，利用故障線路與非故障線路的差異性進行選線，其特點是數學運算較為復雜，且選線結果易受干擾因素影響；2）采用優化算法與傳統淺層學習(人工神經網絡、支持向量機)相結合的方法，其特點是建模較為復雜，選線正確率也有待于進一步提高。

Keras是一個由Python編寫的深度學習框架，便于構建深度學習網絡并進行訓練和測試。本文構建了基于Keras的深度學習網絡，用于故障選線，具有計算簡單、選線正確率高的優點。

1 深度學習算法

深度學習的概念自2006年由Hilton提出后，獲得了巨大的發展[18-19]。深度學習采用了與傳統神經網絡類似的分層結構，如圖1所示，系統包含了輸入層、隱藏層和輸出層。但是二者又有以下不同點：

1）隱藏層不同。傳統神經網絡僅包含一個隱藏層，深度學習網絡可以包含多個隱藏層，而且每層可以包含更多的節點(神經元)。這使得深度學習網絡可以描述更復雜的函數，從而為監督式學習提供了更強大的框架。

2）訓練方法不同。傳統神經網絡采用BP算法進行訓練，往往容易導致收斂于局部最小值；深度學習網絡采用layer-wise的訓練機制，在提高訓練速度的同時，更有利于得到全局最優解。

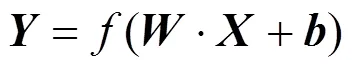
式中：列向量表示該層輸入數據；為系數矩陣，假設該層節點數為m，其上一層節點數為n，則為階矩陣；為m階偏置列向量。

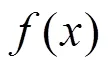
2 選線系統仿真建模

2.1 選線整體流程

圖2為基于深度學習的小電流接地系統故障選線流程圖。首先在PSCAD下搭建某10kV配電網。仿真過程中，令每條線路依次發生單相接地故障，提取包括故障線路在內的所有線路的零序電流分量，利用FFT變換，得到每條線路零序電流的幅值和相角作為樣本數據，將故障線路編號作為標簽數據，對深度學習神經網絡進行訓練，訓練完成后即可利用新數據進行選線。

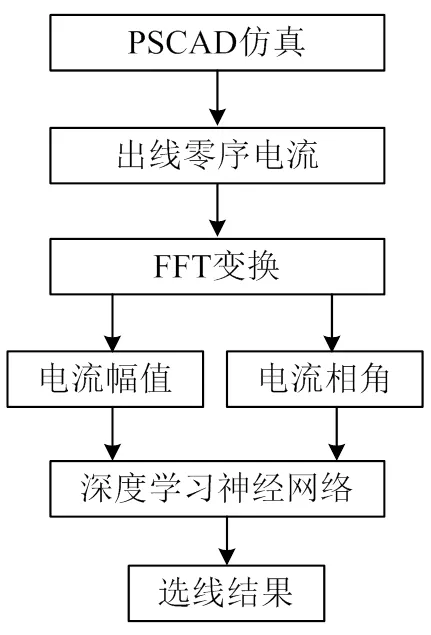
圖2 故障選線流程

2.2 一次系統建模

參照某實際配電網，在PSCAD/EMTDC中搭建仿真系統，如圖3所示。該配電網具有10條出線，變電站位于城區，線路采用電纜、架空線混合方式，相關參數見表1、2。

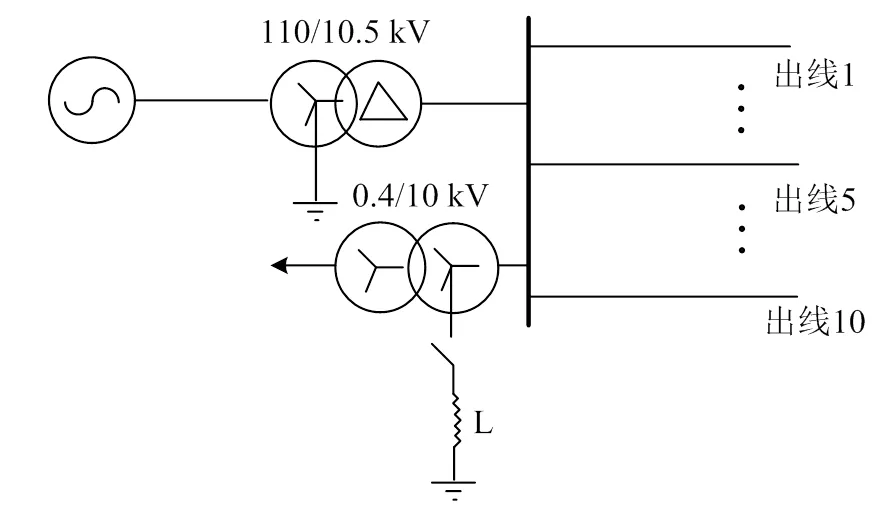
圖3 仿真系統接線示意圖

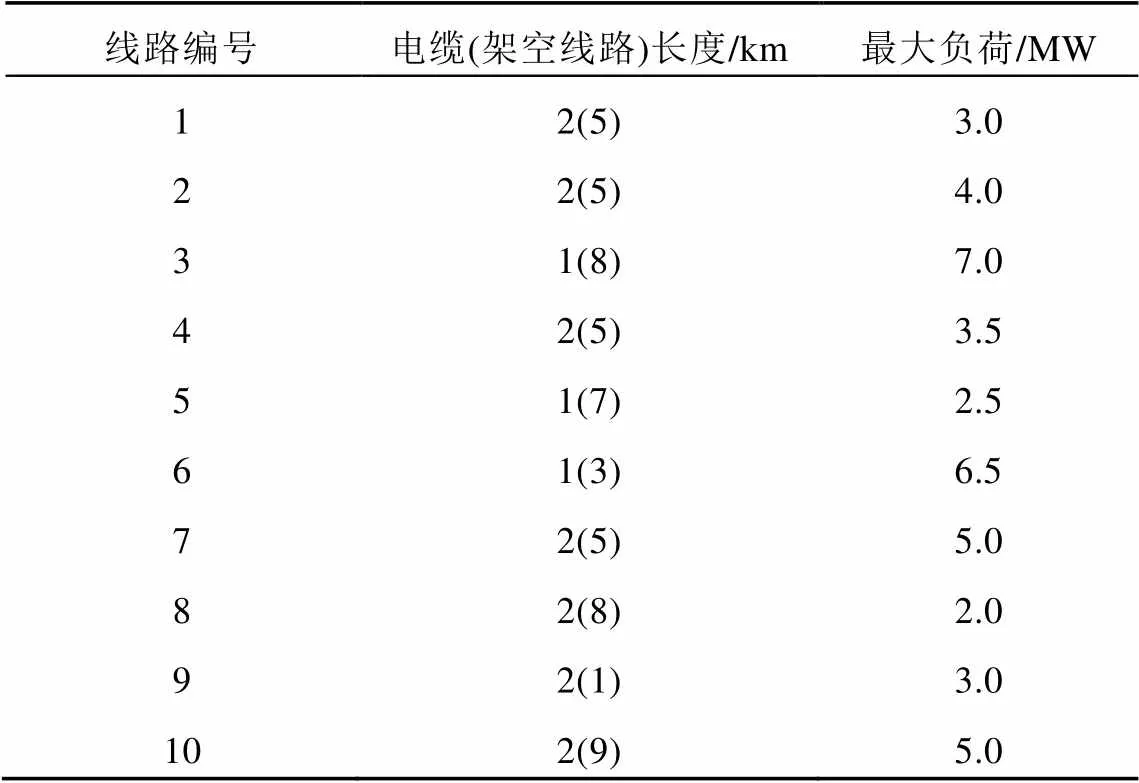
表1 出線參數

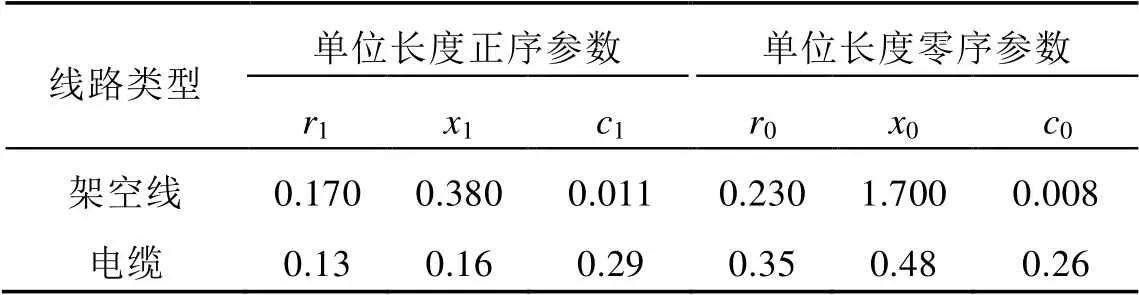
表2 出線阻抗參數

2.3 深度學習網絡架構

深度學習網絡包含可訓練參數和超參數2部分。可訓練參數是指網絡在訓練過程中確定的參數，主要為各層間的連接矩陣以及偏移量。超參數是指需要人為確定的參數，主要包括隱藏層的層數、每層單元數和每層激活函數等。對于超參數的確定，目前尚未有指導性公式可以參考，往往憑經驗通過反復試驗來確定。

通過試驗，本文確定了深度學習神經網絡架構，如表3所示。

表3 深度學習神經網絡架構

注：總參數為39562個，可訓練參數為39562個。

1）輸入層。輸入層接收樣本輸入數據，其節點數取決于樣本數據的數量。本文中采用每條線路零序電流的幅值和相角作為樣本數據，共計10條線路，因此樣本數據的數量為20，即輸入層節點數為20。

2）隱藏層1。隱藏層1將輸入層輸入的樣本數據映射到每一個節點上，其節點數為256，連接矩陣12的階數為256×20=5120，偏置量的階數為256×1，即總參數為5376。

3）丟棄層(Dropout)。丟棄技術是防止網絡過擬合、增強泛化能力的重要手段之一。該層不需要訓練，而是將上一層(隱藏層1)輸出的數據按一定比例丟棄(置零)。

4）隱藏層2。該層確定的節點數為128，連接矩陣階數為128×256，偏置量的階數為128×1，總參數為32896。

5）輸出層。深度學習神經網絡用于解決10條線路中故障線路的選擇問題，其本質上屬于多分類問題。輸出層節點輸出每條線路故障的概率，概率最大者即判定為故障線路。仿真系統中有10條線路，因此輸出層節點數取10。與上一層連接矩陣階數為10×128，偏置量的階數為10×1，總參數為1290。

6）各層激活函數。采用激活函數可以使神經網絡表示復雜的非線性函數。深度學習神經網絡中，各隱藏層采用Relu函數作為激活函數，輸出層輸出的是每條線路的故障概率，因此采用Softmax函數作為激活函數。

3 算例分析

3.1 中性點不接地方式

系統采用中性點不接地運行方式，每條線路分別采用單相直接接地、經500Ω電阻接地、經1000Ω電阻接地3種故障類型，經FFT采樣后，得到1850組樣本。把所有樣本隨機分成訓練集、驗證集、測試集3組。其中測試集為150組樣本，訓練集與驗證集比例為9?1。

為了加速深度學習神經網絡訓練過程中的收斂，需要對樣本數據進行預處理。數據預處理主要包括以下2個方面：

1）特征數據歸一化。可以利用式(2)將所有的特征數據都處理到(0,1)區間范圍內。

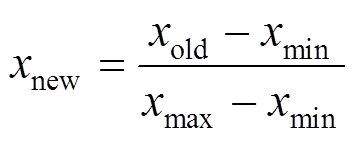
2）標簽數據二值化。原始標簽數據為故障線路編號，為了與網絡輸出的概率值相對應，需要將其轉化為十位二進制數據。每一位二進制數據對應一條線路，其中非故障線路對應數據為0，故障線路對應數據為1。如第3條線路發生故障，其原始標簽為3，二值化處理后的數據為0010000000。

將經過預處理的樣本數據輸入到搭建好的深度學習神經網絡中進行訓練，訓練迭代次數為50次。損失函數值曲線如圖4所示，可以看出，隨著迭代次數的增加，損失函數值越來越小，表明網絡輸出值與目標值(標簽值)越來越接近。

圖5為精確度曲線，可以看出，隨著訓練次數的增加，網絡在訓練數據集和驗證數據集上表現出來的預測精確度越來越高。

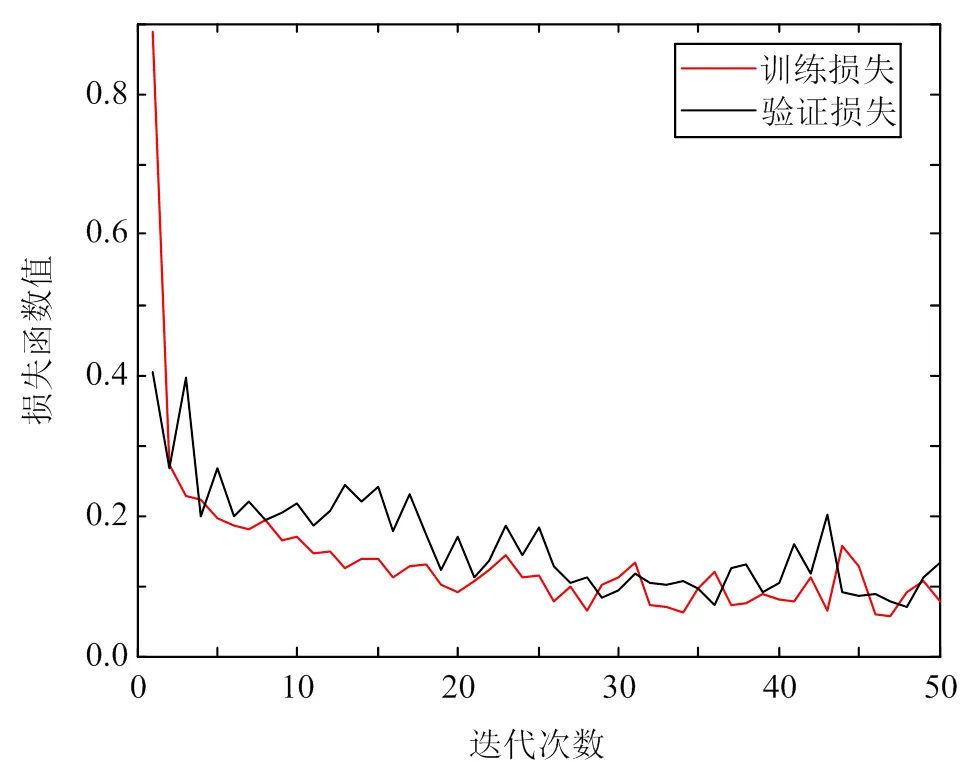
圖4 損失函數值曲線?1

圖5 精確度曲線?1

訓練結束后，利用預留的150組測試集數據對訓練好的神經網絡進行測試。測試結果如表4所示。表4中主對角元素的數值表示相應線路故障時判斷正確的次數；非主對角線元素的數值表示判斷錯誤的次數。以第1行、第1列數據為例，該數據值為11，表示線路1發生故障時，判斷正確的次數為11；線路1所在列的非主對角線元素值均為0，表示未發生誤判。作為對比，再以線路8所對應的第8列數據為例進一步說明。該線路對應的主對角線元素值為14，即判斷正確的次數為14。非主對角線元素有2個非零值，其中：第1個非零值位于第8列第2行，數值為1，其含義為實際發生故障的線路為線路8，判斷結果為線路2，判斷錯誤次數為1次。同理，第2個非零值位于第8列第3行，數值為1，表示實際故障發生在線路8，判斷結果為線路3，判斷錯誤次數為1次。綜上分析，測試集樣本數量為150，判斷正確次數(主對角線元素之和)為148次，判斷錯誤次數(非主對角線元素之和)為2次，正確率達到98.7%。

表4 測試結果混淆矩陣?1

3.2 中性點經消弧線圈接地方式

系統采用中性點經消弧線圈接地運行方式，過補償度為10%。每條線路分別采用單相直接接地、經500Ω電阻接地、經1000Ω電阻接地3種故障類型，經FFT采樣后，得到1930組樣本。把所有樣本隨機分成訓練集、驗證集、測試集3組。其中測試集為150組樣本，訓練集與驗證集比例為9?1。

訓練過程中的損失函數值曲線和預測精確度曲線分別如圖6、7所示。

訓練結束后，利用測試集數據進行測試，測試結果如表5所示。可以看出，線路7發生故障時，誤判次數較多，其中誤判為線路3故障的次數為1次，誤判為線路5故障的次數為2次，誤判為線路6故障的次數為1次，總計誤判次數為4次。測試集樣本數量為150，判斷正確次數(主對角線元素之和)為145次，判斷錯誤次數(非主對角線元素之和)為5次，正確率達到96.7%。

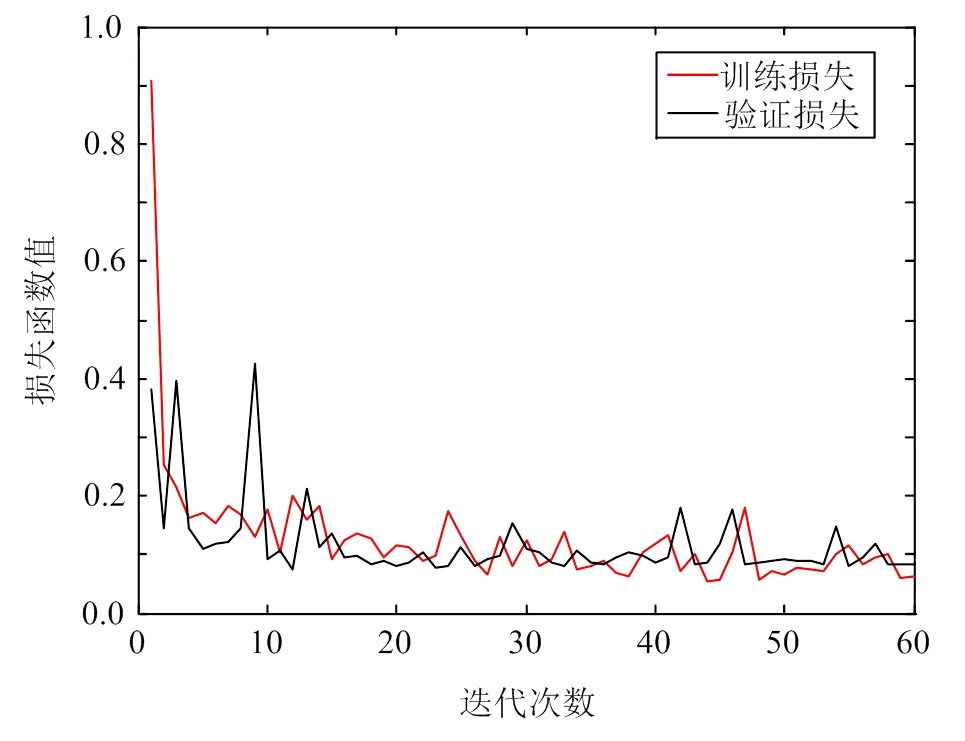
圖6 損失函數值曲線?2

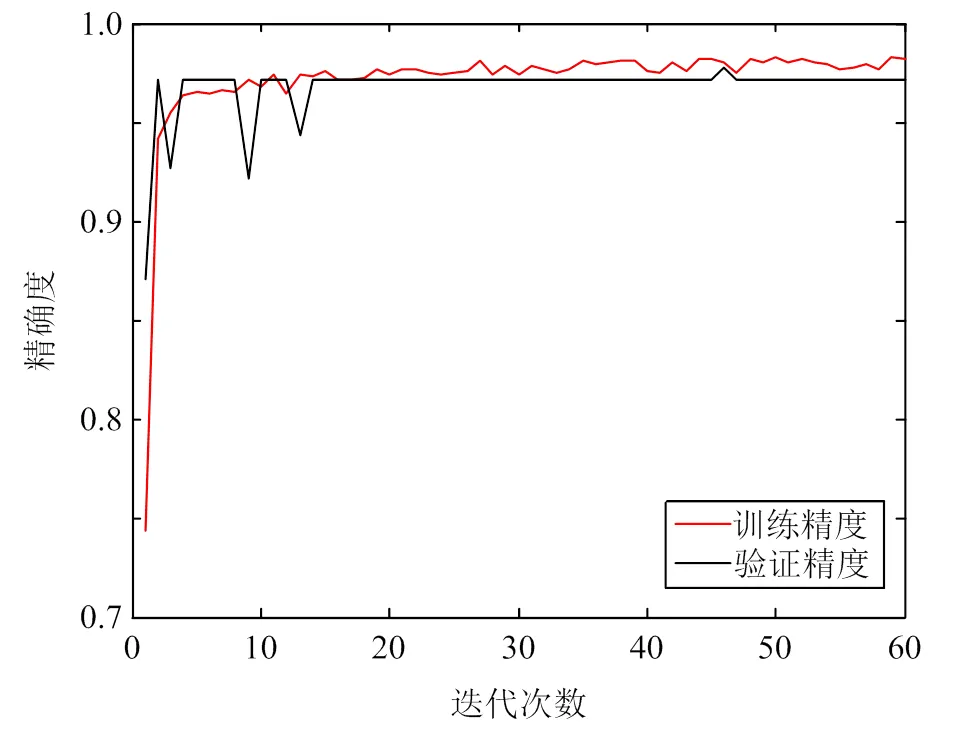
圖7 精確度曲線?2

表5 測試結果混淆矩陣?2

3.3 考慮故障點電弧的仿真模型

前述仿真過程中，未考慮接地點產生電弧的情況。為盡可能真實地反映實際系統情況，參照文獻[20]中的方法，建立了Mayr電弧模型。經FFT采樣后，得到1930組樣本。把所有樣本隨機分成訓練集、驗證集、測試集3組。其中測試集為150組樣本，訓練集與驗證集比例為9?1。

訓練過程中的損失函數值曲線和預測精確度曲線分別如圖8、9所示。

訓練結束后，利用測試集數據進行測試，測試結果如表6所示。可以計算出，在電弧影響下，判斷正確率下降至94.7%。

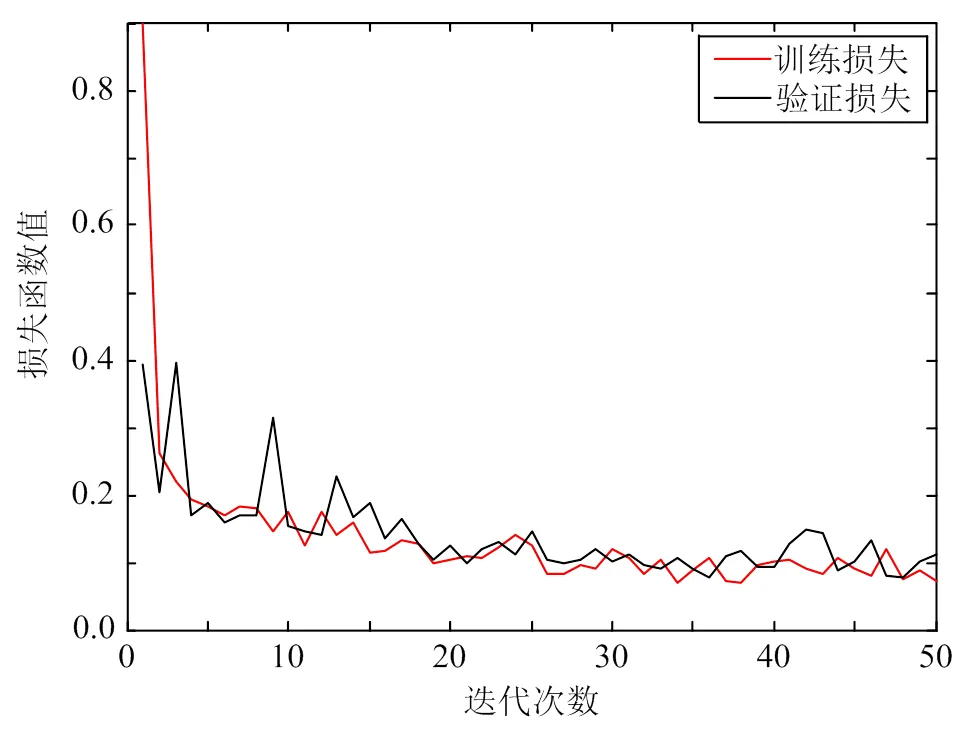
圖8 損失函數值曲線?3

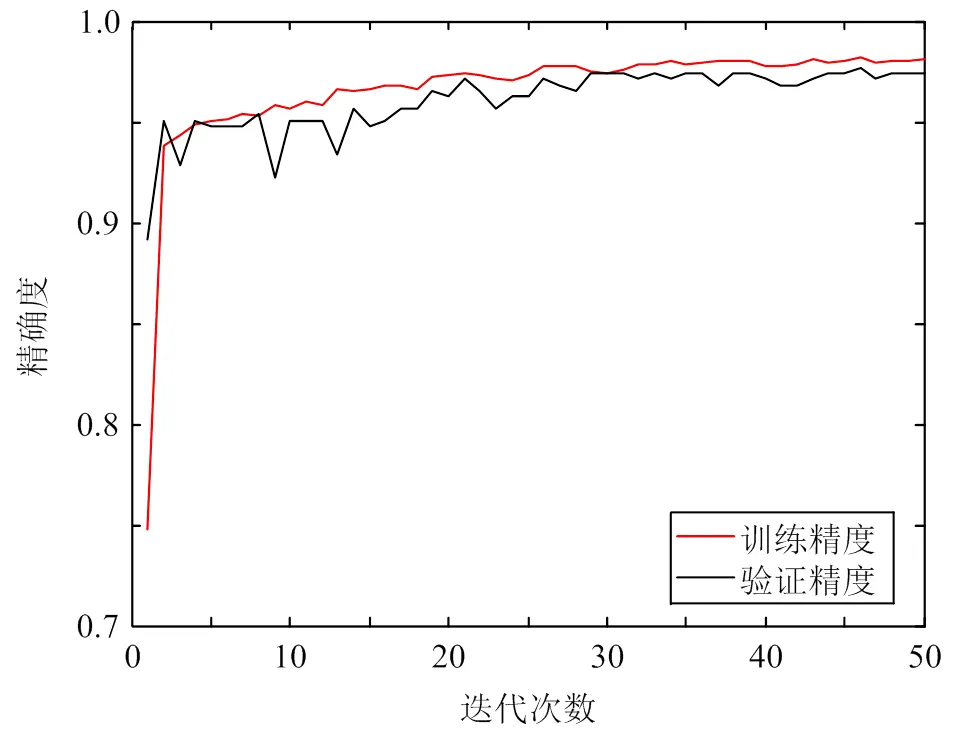
圖9 精確度曲線?3

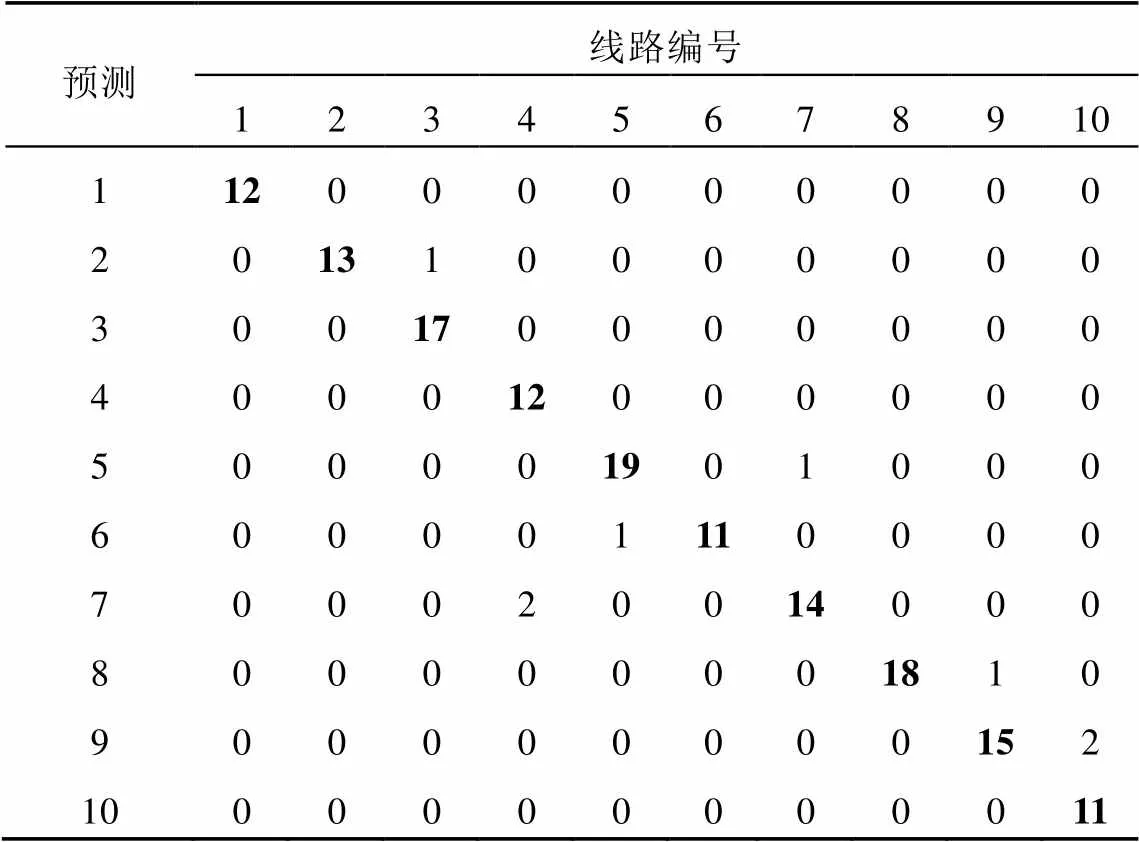
表6 測試結果混淆矩陣?3

4 結論

構建了基于深度學習框架的小電流接地系統單相接地故障的選線模型。在PSCAD下搭建仿真模型，通過仿真獲得訓練數據。利用仿真所得數據對深度學習神經網絡進行訓練，將訓練好的模型用于單相接地故障線路的選擇。結果表明，對于中性點不接地系統的單相接地故障，選線正確率達到了98.7%；對于中性點經消弧線圈接地系統的單相接地故障，選線正確率達到了96.7%，且選線結果不受過渡電阻影響；引入電弧模型后，選線正確率仍能保持94.7%，說明該方法有效。

[1] 陳皓，田新和，高傳薪，等．直流微電網故障定位研究綜述[J]．廣東電力，2019，32(7)：44-51．

[2] 徐棟杰，劉文澤，李曉華．開關型消弧裝置的故障選相及選線方法[J]．廣東電力，2019，32(1)：125-131．

[3] 汪洋．基于小波分解-暫態信號的綜合極性比較故障選線法[J]．電網與清潔能源，2017，33(6)：59-66．

[4] 劉宏偉，朱東坡，劉捷，等．配電網中性點經小電阻接地方式下的小電阻選取[J]．電網與清潔能源，2018，34(7)：31-37．

[5] 龍茹悅，黃純，湯濤，等．一種諧振接地系統的配電線路接地故障選線新方法[J/OL]．電力系統保護與控制：1-9[2019-11-21]．https://doi.org/10.19783/j.cnki.pspc.181495.

[6] 方毅，薛永瑞，宋華茂，等．諧振接地系統高阻接地故障暫態能量分析與選線[J]．中國電機工程學報，2018，39(19)：5636-5645．

[7] 朱永利，尹金良．人工智能在電力系統中的應用研究與實踐綜述[J]．發電技術，2018，39(2)：106-111．

[8] 蔣凱，童曉陽，梁晨．基于隨機矩陣的配電網故障選線方法研究[J]．電工技術，2018(13)：1-4．

[9] 羅浩杰，張棟柱，李民強，等．基于人工神經網絡小電流接地選線方法研究[J]．四川電力技術，2016，39(6)：36-40．

[10] 薛太林，侯雋朗，張建新．基于GA優化BP神經網絡小電流接地系統故障選線方法[J]．電氣自動化，2018，40(2)：66-69．

[11] 但揚清，趙偉，朱艷偉，等．基于ABC-DNN的小電流接地故障選線方法[J]．智慧電力，2019，47(4)：46-52．

[12] 徐銘銘，高淑萍，常仲學，等．基于模型識別的消弧線圈接地系統單相接地選線方法[J]．電力系統保護與控制，2018，46(2)：73-78．

[13] 沈興來，楊智．基于故障全信息的自適應模糊融合選線技術[J]．電力工程技術，2017，36(6)：90-95．

[14] 劉謀海，方濤，姜運，等．基于高頻分量相關度分析的故障選線方法[J]．電力系統及其自動化學報，2017，29(2)：101-106．

[15] 陳奎，陳博博．基于改進暫態相關分析和支持向量機的電弧故障選線研究[J]．電力系統保護與控制，2016，44(24)：66-73．

[16] 邵祥，郭謀發，游林旭．基于改進DTW的接地故障波形互相關度聚類選線方法[J]．電力自動化設備，2018，38(11)：63-71．

[17] 魏鑫，舒乃秋．基于Hausdorff距離的配電網單相接地故障選線方法[J/OL]．電力系統及其自動化學報：1-12[2019-11-21]．https://doi.org/10.19635/j.cnki.csu-epsa.000244．

[18] 周懷春，胡志方，郭建軍，等．面向智能發電的電站燃煤鍋爐在線運行優化[J]．分布式能源，2019，4(3)：1-7．

[19] 潘玉松，陳旭偉，張鵬．傳統火電廠建設智慧電廠的典型方向及構架體系[J]．分布式能源，2018，3(5)：48-53．

[20] 竇婷婷，姚元璽，陳鵬，等．基于ATP-EMTP的電弧建模及工程仿真[J]．山東大學學報(工學版)，2019，48(4)：102-108．

Fault Line Selection Method of Small Current Grounding System Based on Deep Learning

ZHANG Guodong1, PU Haitao1, LIU Kai2

(1. Department of Electrical and Information, Shandong University of Science and Technology, Jinan 253500,Shandong Province, China; 2. Luoyang Power Supply Company, Luoyang 471000, Henan Province, China)

At present, the single-phase grounding fault line selection problem of small current grounding system has not been completely solved. In order to improve the success rate of single-phase grounding fault line selection, a new method based on deep learning network was proposed. Firstly, the simulation model of neutral un-grounded system was built by PSCAD. By setting the fault of each line under different grounding resistors, the sample data based on the zero sequence current value and phase angle of each line was obtained out. The sample data was divided into three parts: training set, verification set, and test set. Secondly, a deep learning neural network was constructed based on Keras, and the network was trained using the training set and validation set. Finally, the trained model was tested using the test set. The results show that the method has the characteristics of simple modeling, high success rate and no influence of transition resistance.

small current grounding system; single- phase grounding fault; fault line selection; deep learning

10.12096/j.2096-4528.pgt.19103

2019-07-06。

教育部產學合作協同育人計劃項目(201702064021)；山東科技大學濟南校區教研項目(JNJG2017203)。

Project Supported by Ministry of Education's Cooperative Education Program Project (201702064021); Research Project of Jinan Campus of Shandong University of Science and Technology (JNJG2017203).

(責任編輯 尚彩娟)