基于Copula函數的渡槽結構地震動易損性分析*

張建偉， 張 帥， 張翌娜， 黃錦林, 李兆恒

(1.華北水利水電大學水利學院 鄭州，450046) (2.水資源高效利用與保障工程河南省協同創新中心 鄭州，450046)

(3.河南省水工結構安全工程技術研究中心 鄭州，450046) (4.黃河水利職業技術學院土木與交通學院 開封，475004)

(5.廣東省水利水電科學研究院 廣州，510635)

引 言

地震易損性是指在不同強度的地震作用下，預測某一結構或構件超過某一損傷程度的條件概率，是基于性能抗震設計的基礎，也是結構地震風險分析的主要組成部分[1]。隨著我國南水北調工程等水利工程的建設，修建了一系列規模大、技術難度高的渡槽工程，針對渡槽的地震易損性分析就顯得尤為迫切。

關于地震易損性的研究方法一般有兩種表達：離散形式的易損性指標矩陣和連續形式的易損性曲線[2]。易損性曲線受限條件少，使用方便，應用更加廣泛。目前關于地震易損性的分析常以單一構件的易損性曲線來表達整個系統結構的損傷狀態，不考慮各構件之間的相互聯系，該方法雖簡單，但不能對整個系統的易損性進行準確評估。如果要準確考慮各構件的影響，則需要充分了解結構構造細節以及各構件之間的相關關系，建立各構件之間的聯合分布函數模型。引起結構損傷的因素眾多，這些因素不僅本身機理復雜，且各部分之間相互影響，不同結構都有自己所特有的細節，直接建立系統的易損性曲線較為困難[3]。Tavares等[4]采用1階界限法，不考慮構件損傷概率之間的相關性，得到上界和下界來估計整個系統的易損性，但界限范圍較寬，結果誤差較大。Nielson等[5]通過Monte Carlo法得到整個系統結構的地震易損性曲線，但其需要大量的數值抽樣，工作量較大，操作麻煩，且假設構件間的地震需求是線性的，與實際非線性不相符。

近些年，數學領域發展的Copula理論為不完備概率信息條件下相關變量的聯合分布函數建立提供了一種新的途徑[6]。Copula作為邊緣分布函數的連接函數，邊緣分布函數的形式不會對其產生影響，故Copula函數可以和邊緣分布函數分開考慮，能夠有效解決構件需求之間的相關性[7]。Copula函數理論最先在金融領域中得到應用[8]，在水文學[9]以及結構工程[10]中也得到了進一步的應用和發展。筆者基于Copula函數將構件地震需求間的相關性和構件的邊緣分布函數分離，建立橡膠支座和排架地震需求的聯合分布模型，在得到橡膠支座和排架的地震易損性曲線后，通過Copula函數，得到渡槽系統的易損性曲線，并將其與1階界限法結果比較，證明該方法的準確性和優越性。

1 基于Copula函數的聯合分布函數構造方法

二維Copula函數定義為：在[0,1]2定義域內，邊緣分布函數在[0,1]內為均勻分布的二維聯合分布函數，變量X1和X2的聯合分布函數F(x1,x2)[11]可表示為

F(x1,x2)=C(F1(x1),F2(x2);θ)=C(u1,u2;θ)

(1)

其中：u1，u2為X1,X2的邊緣分布函數F1(x1),F2(x2)；C為Copula函數；θ為Copula函數所對應的相關參數。

若F1,F2為連續函數，則C是唯一的。若x1,x2對應的邊緣密度函數分別為f1(x1),f2(x2)，則x1,x2所對應的聯合概率密度函數為

f(x1x2)=f1(x1)f2(x2)c(F1(x1),F2(x2);θ)

(2)

c(F1(x1),F2(x2)；θ)=?2C(u1,u2；θ)/?u1?u2

(3)

其中：c為Copula函數的密度函數。

若已知X1和X2的邊緣分布函數以及Copula函數，則可以建立X1,X2的二維分布模型。Copula函數的相關參數θ可以通過Spearman秩相關系數τ求出，變量X1,X2間的相關系數τ與Copula函數的C(u1,u2；θ)存在如下對應關系

(4)

對于Gaussian Copula函數來說，相關參數θ可由下式解得

(5)

對于Clayton和Cclayton Copula函數，相關參數θ可由下式解得

(6)

2 地震易損性曲線

2.1 構件易損性

渡槽是由排架以及橡膠支座等基本構件組成，基本構件的易損性是求解渡槽系統易損性的基礎。在地震作用下，構件的易損性[12]可以用構件的地震需求Sd超過構件的抗震能力Sc的概率來表示

Pf=P(Sd≥Sc)

(7)

目前關于地震需求分析中，認為各構件的抗震能力和地震需求均服從對數正態分布，即構件的抗震能力Sc和地震需求Sd[13]可表示為

(8)

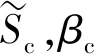
由概率地震需求分析可知，構件地震需求Sd與地震動參數IM服從指數關系

Sd=a(IM)b

(9)

將式(9)轉換為對數空間，得

ln(Sd)=bln(IM)+ln(a)

(10)

由中心極限定理可知，在某一極限狀態下，構件縱向與橫向的失效概率為

(11)

將式(10)代入式(11)，得構件縱向與橫向的失效概率

(12)

單個構件縱向與橫向的地震易損性曲線，其實現流程如圖1所示。

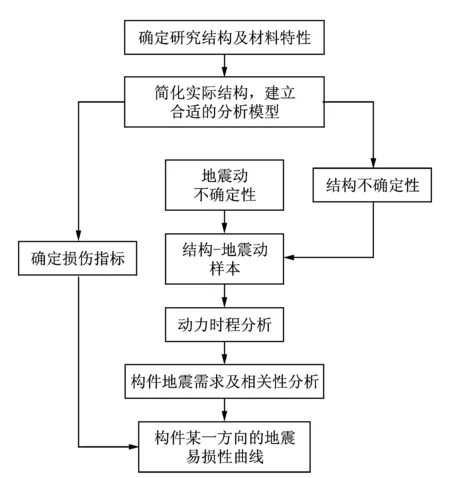
圖1 單個構件縱向與橫向的地震易損性曲線實現流程

根據橡膠支座和排架的橫向與縱向的失效概率，將兩個方向地震作用效應進行耦合，可以得到橡膠支座和排架的失效概率

(13)

其中：P1，P2分別為橡膠支座和排架的失效概率；PX1，PX2分別為橡膠支座和排架的縱向失效概率；PY1，PY2分別為橡膠支座和排架的橫向失效概率。

將式(12)得到的結果代入式(13)，可得排架、橡膠支座的地震易損性曲線。

2.2 系統易損性及Copula函數的積分方法

渡槽在地震作用下，排架和橡膠支座的損傷較為普遍，且兩者都會影響渡槽功能的發揮，可將渡槽結構看作由排架和橡膠支座構成的串聯系統，故考慮構件相關性的渡槽系統失效概率為

Pfs=P(g1≤0∪g2≤0) =P(g1≤0)+

P2(g2≤0)-p(g1≤0,g2≤0)=

Pf1+Pf2-C(Pf1,Pf2)

(14)

其中：g1和g2為橡膠支座和排架所對應的功能函數；Pf1,Pf2為橡膠支座及排架所對應的失效概率。

將橡膠支座和排架的失效概率代入式(14)，得到整個渡槽系統的易損性曲線，其中Copula函數是整個渡槽系統易損性求解的關鍵一步。數學中存在多種Copula函數可以描述變量間的相關性，由似然函數赤池信息準則(Akaike information criterion，簡稱AIC)可知，Gassian Copula函數和Frank Copula函數能夠較好地反映構件地震需求間的相關性，故選擇上述函數來計算渡槽系統的易損性。

Gaussian Copula函數二維表達式為

(15)

Frank Copula二維函數表達式為

(16)

其中：Φ-1(·)為標準正態分布函數的逆函數。

3 計算實例

3.1 模型建立

以某工程總干渠5#渡槽中的一跨為例，對渡槽進行易損性分析。該渡槽為鋼筋混凝土U形薄壁結構，兩端采用盆式橡膠支座，渡槽一跨長度為12 m，基礎底端到槽頂高度為16.5 m，槽內設計水深3.05 m，排架橫截面的尺寸為1.1 m×1.4 m。

渡槽槽身混凝土采用C30，密度為2 484 kg/m3，彈性模量為3.11×104MPa，泊松比為0.167；渡槽排架及基礎混凝土采用C20，密度為2 425 kg/m3，彈性模量為2.56×104MPa，泊松比為0.167；鋼筋密度為7 800 kg/m3，彈性模量為20×104MPa；盆式橡膠支座的密度為2 500 kg/m3，彈性模量為0.386×104MPa，泊松比為0.35。算例模型采用ANSYS有限元軟件建模，渡槽槽身采用殼單元SHELL63模擬；排架及基礎采用實體單元SOLID185模擬；橡膠支座采用彈簧單元模擬，水平向采用COMBIN40單元，垂直向采用COMBIN14單元；渡槽頂梁及拉桿采用梁單元BEAM188模擬；動水壓力采用附加質量MASS21施加。渡槽有限元模型如圖2所示，計算工況為設計工況。

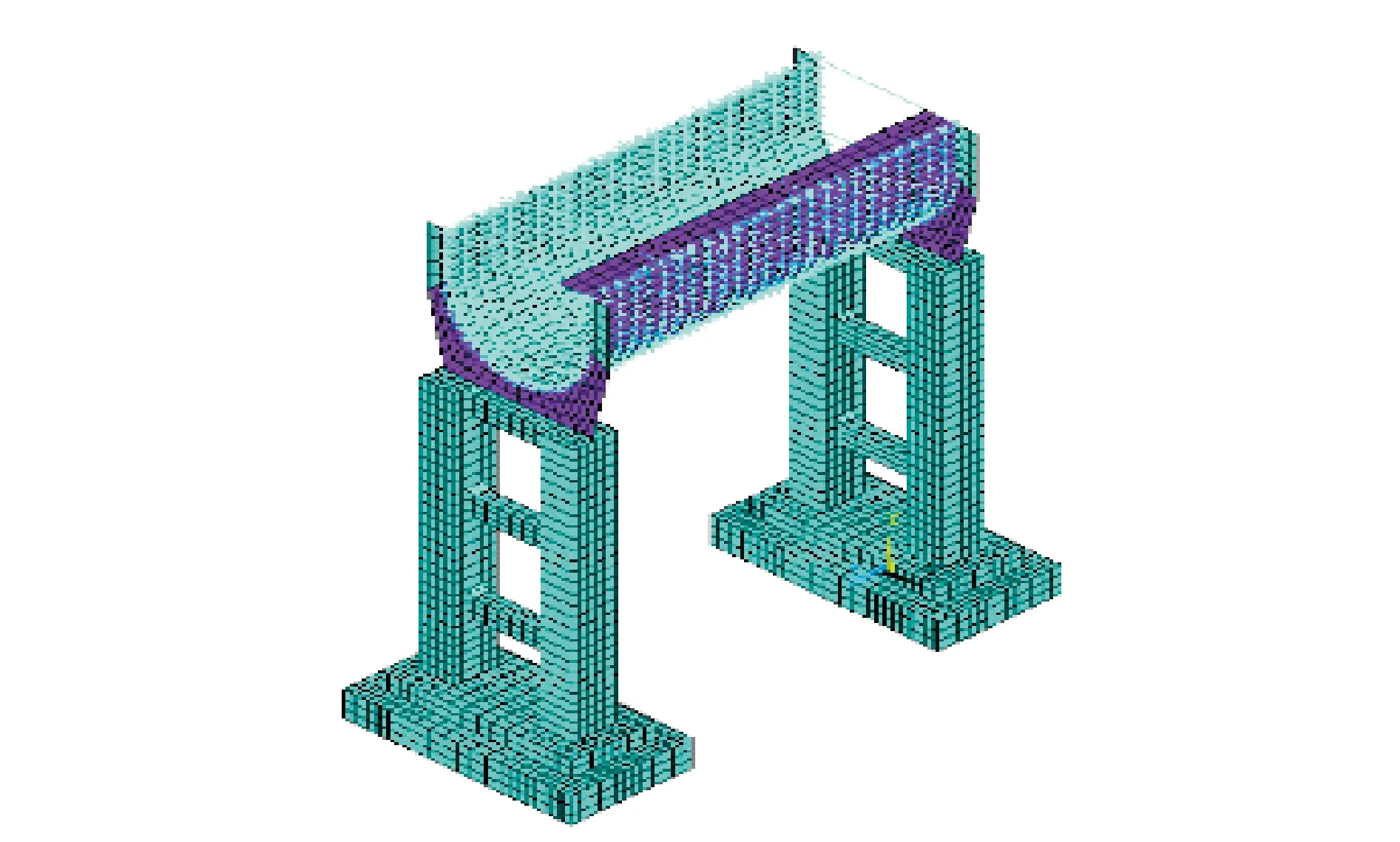
圖2 5#渡槽有限元模型

3.2 模型不確定性

影響渡槽易損性分析的不確定性因素可分為結構參數不確定性和地震動不確定性，在對渡槽進行易損性分析時，必須考慮這些不確定性因素帶來的影響。

結構參數不確定性是指由于知識缺乏或建模誤差所導致的不確定性，主要包括構件尺寸、材料、質量、阻尼和邊界條件等。本渡槽模型考慮的結構參數不確定性與分布如表1所示，根據結構參數的分布特征，將每個參數的取值等概率分為12組，去掉其中1組最大值和1組最小值，保留10組，然后通過拉丁超立方抽樣法，得到10個綜合考慮結構參數不確定性的渡槽樣本，從而避免大量數值抽樣。

挑選合適的地震動輸入是地震易損性分析的基礎。地震動不確定性主要包括地震動本身的隨機性、方向效應、入射角和空間變異性。為了能夠準確得到渡槽地震需求，充分考慮地震動的隨機性，首先從太平洋地震工程中心強震數據庫中選擇50條地震動記錄，所選地震動的峰值加速度(peak ground acceleration，簡稱 PGA)分布如圖3所示，然后將拉丁超立方抽樣所得的10個渡槽模型和50條地震動記錄進行隨機匹配，進行地震時程分析計算。進行地震動力計算時，動彈模取值為1.3倍的靜彈模，地基模擬采用局部人工邊界無質量地基，并考慮三方向地震對結構影響，用APDL編程語言，從地基底部及四周輸入地震波數據的峰值加速度進行等效應力輸入。

表1 結構參數不確定性及其分布

Tab.1 Uncertainties and their distribution of structure parameters

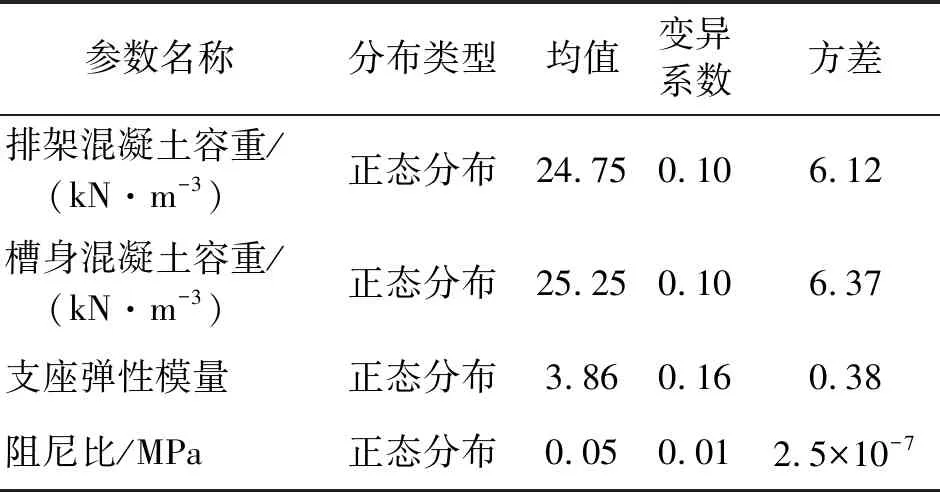
參數名稱分布類型均值變異系數方差排架混凝土容重/ (kN·m-3)正態分布24.750.106.12槽身混凝土容重/ (kN·m-3)正態分布25.250.106.37支座彈性模量正態分布 3.860.160.38阻尼比/MPa正態分布 0.050.012.5×10-7

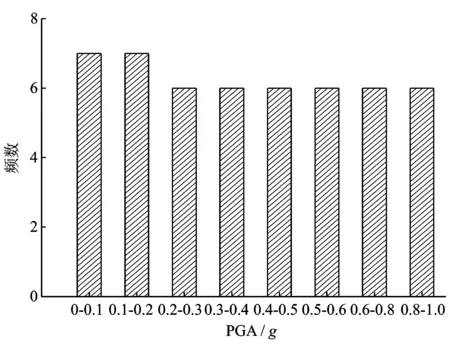
圖3 地震動的PGA分布

3.3 構件地震需求

地震作用下，渡槽的橡膠支座和排架較易發生損傷。為有效地描述渡槽的損傷狀態及損傷程度，以排架縱、橫向位移延性比(μL，μT)以及橡膠支座縱、橫向位移(bL，bT)作為構件的地震需求參數。

根據時程分析結果，通過最小二乘法對構件的地震需求和地震動參數進行回歸分析，得到構件地震需求模型。排架縱向地震需求模型如圖4所示，總結如表2所示。

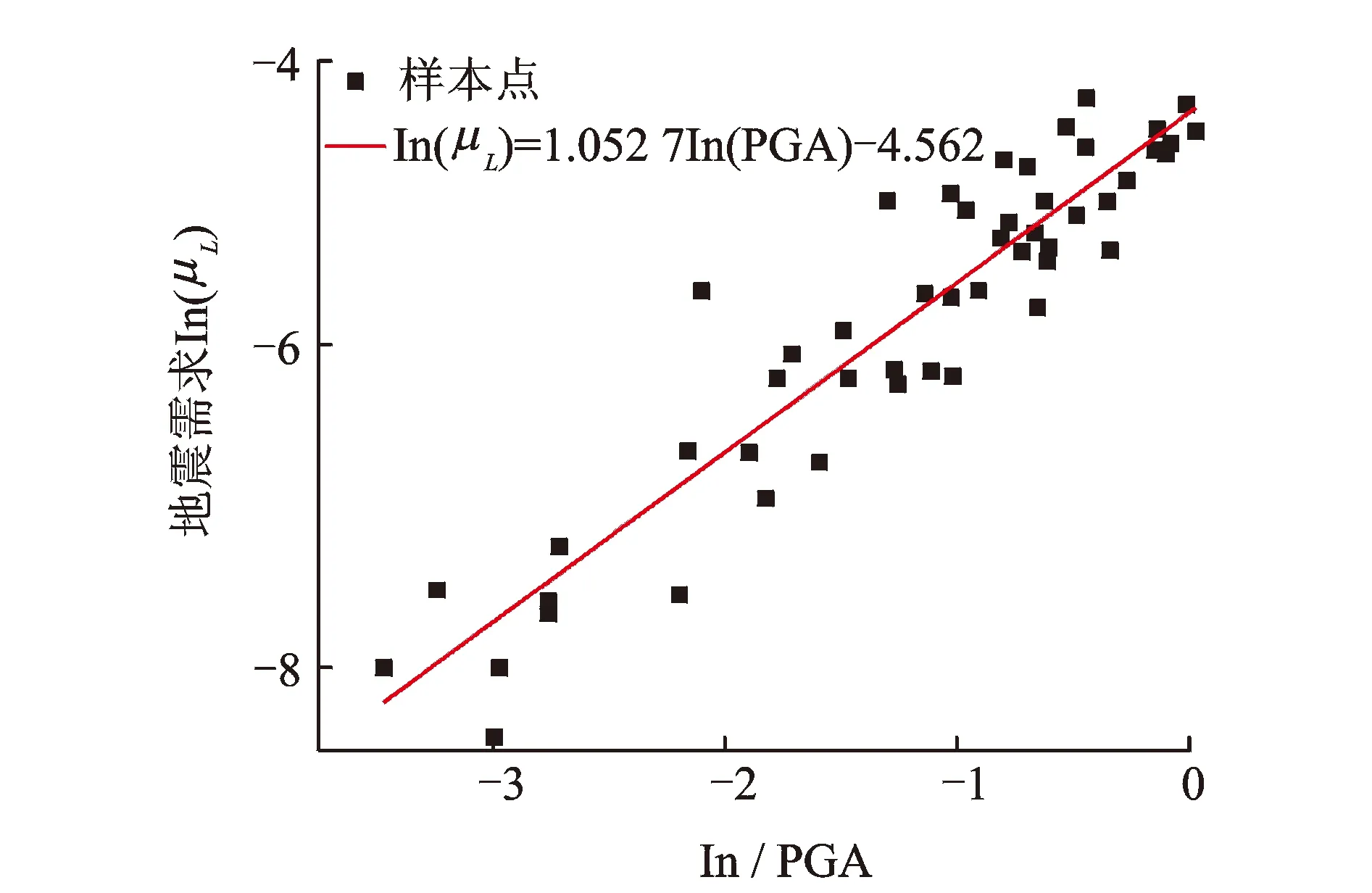
圖4 排架縱向地震需求模型

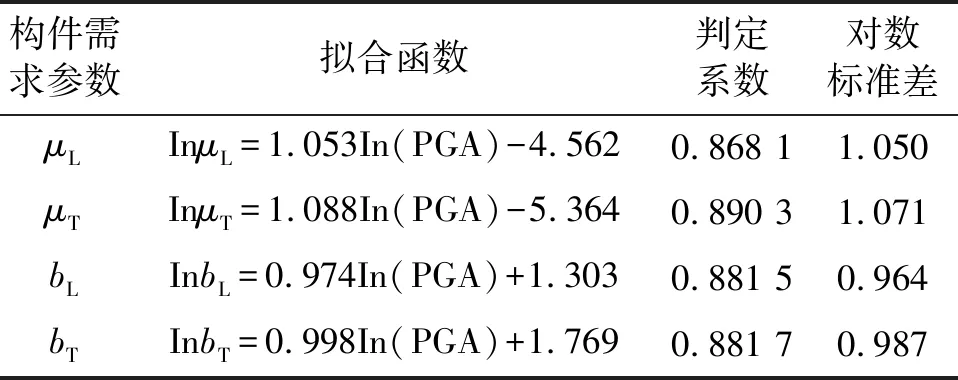
表2 渡槽構件地震需求模型

3.4 構件損傷指標

結構在地震作用下的損傷程度可分為4個等級：輕微破壞、中等破壞、嚴重破壞和完全破壞[14]。為了對各損傷狀態下的易損性進行準確評估，需要定義各損傷狀態下構件的損傷指標。

對于排架而言，各損傷狀態下的位移延性比μd[15]可表示為

(17)

其中：Δ為墩頂極限位移；Δcy1為縱向鋼筋首次屈服時的墩頂位移。

排架在地震作用下的4種損傷程度的定性描述和損傷指標定量描述如表3所示。其中：μcy1為單根

表3 排架損傷狀態及損傷指標描述

Tab.3 Damage status and description of damage index of column of bent

損傷狀態損傷描述損傷指標輕微破壞混凝土發生輕微剝落,有微小裂縫產生μcy1<μd≤μcy中等破壞混凝土發生開裂,裂縫不斷擴展,結構抗力不斷降低μcy<μd≤μc4嚴重破壞局部混凝土壓碎,形成較大裂縫μc4<μd≤μcmax完全破壞核心混凝土壓碎,發生倒塌μd>μcmax

鋼筋首次屈服時位移延性比；μcy為等效屈服位移延性比；μc4為截面邊緣鋼筋混凝土壓應變達到0.004時的位移延性比；μcmax為最大破壞位移延性比。

通過彎矩-曲率分析和Pushover方法可得到各損傷狀態下排架的損傷指標，結果如表4所示。

橡膠支座是渡槽結構中的一個重要構件，同時也是較容易發生損傷的構件。支座的損傷狀態與其變形大小密切相關，一般采用其變形大小作為損傷指標[16]。本研究橡膠支座的4種損傷狀態，用其允許相對位移與剪應變為100%時的相對位移之比來定義，4種損傷狀態的相對位移比分別為1.0，1.5，2.0和2.5。由橡膠支座的物理參數與幾何尺寸，可得橡膠支座在4種損傷狀態下的損傷指標，如表4所示。其中：μL，μT為排架縱、橫向位移延性比；bL，bT為橡膠支座縱、橫向位移。

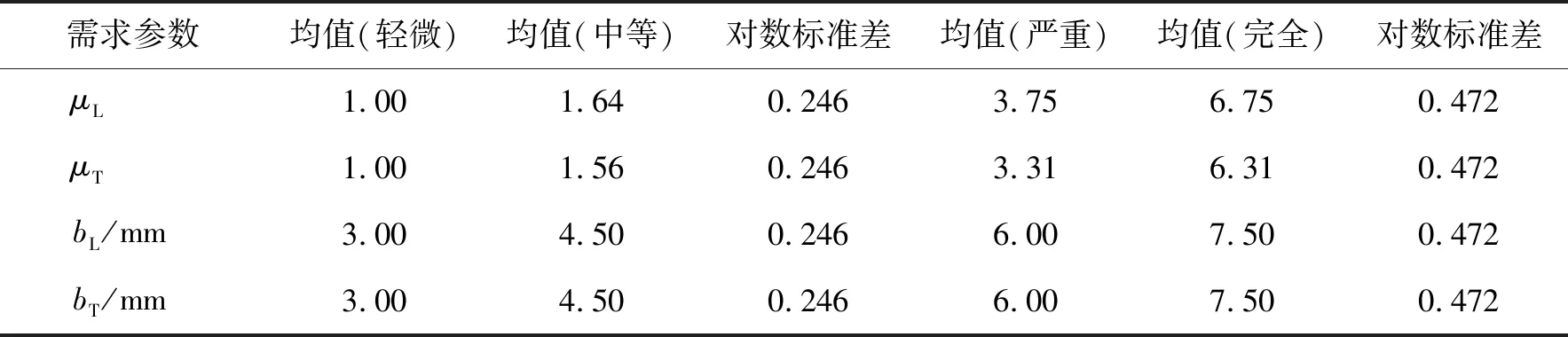
表4 構件損傷指標

由結構參數不確定性可知，在不同損傷狀態下，結構的抗震能力也具有不確定性。參考Nielson[17]提出的變異系數(V)來描述構件抗震能力的不確定性。對于前2種損傷狀態變異系數取值為0.25，對于后2種損傷狀態變異系數取值為0.5。當構件的抗震能力服從對數正態分布時，對數標準差和變異系數存在如下關系

(18)

由式(18)便可求得橡膠支座、排架在各損傷狀態下的抗震能力對數標準差，如表4所示。

4 計算分析

4.1 構件易損性

將排架和橡膠支座的地震需求模型和損傷指標代入式(12)、式(13)，可得排架和橡膠支座的易損性曲線，如圖5所示。

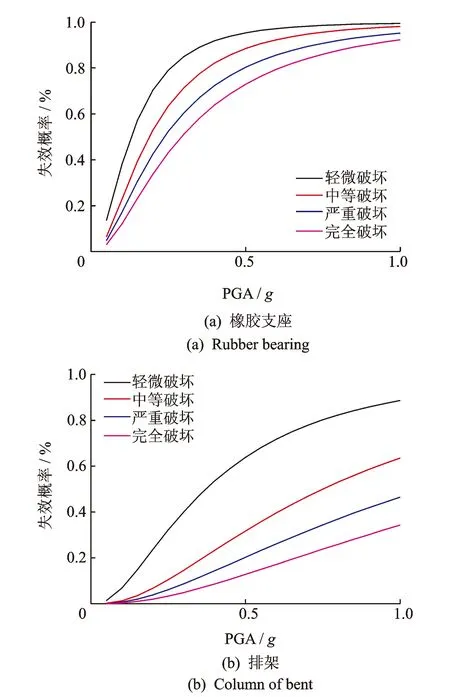
圖5 渡槽構件易損性曲線

由圖5可知：在地震動峰值加速度小于0.1g時，排架、橡膠支座發生損傷的概率均較小；橡膠支座在4種損傷狀態下的失效概率明顯大于排架；橡膠支座與排架相比，在4種損傷狀態下的失效概率變化幅度較小。

4.2 渡槽系統易損性

4.2.1 Copula函數方法

利用Matlab的Copulafit函數計算Gassian Copula和Frank Copula函數中的相關參數，繪制Gassian Copula和Frank Copula的密度函數圖和分布函數圖。通過式(14)～(16)可得整個渡槽系統的易損性曲線。

4.2.2 1階界限法

為檢驗Gassian Copula函數和Frank Copula函數的準確性，將其與1階界限法結果進行比較。采取1階界限法計算渡槽整體失效概率的上界與下界，來逼近整個系統的易損性。整個渡槽的失效概率[18]可表達為

(19)

其中：Pfs為整個渡槽的失效概率；Pi為第i個構件的失效概率；n為構件個數。

假設結構系統的各種失效模式是正相關的，即相關系數ρ>0，則下界為單個構件易損性的最大值。為直觀比較，將其與Copula函數得到的渡槽系統易損性曲線放在同一圖中比較，如圖6所示。

由圖6可知，通過Copula函數得到的渡槽系統失效概率在整個地震動強度內都處于1階界限法的上界和下界之間，且更靠近于上界。用下界描述系統的易損性會明顯降低整體結構的易損性。兩種Copula函數結果對比可知，通過Frank Copula函數和Gassian Copula函數計算得到的渡槽系統易損性結果接近，4種破壞狀態下的最大偏差分別為3.1%，4.2%，5.1%和4.6%。隨著地震動強度的增大，通過1階界限法所得到的上、下界的差值變的越來越大。因此，當地震動強度較大時，采用1階界限法的下界來估計渡槽系統的易損性較為保守。

5 結 論

1) Copula函數不僅能準確地描述橡膠支座和排架的非線性相關特性，還能簡化多元聯合概率密度函數的建模過程，為研究渡槽構件地震需求之間的相關性提供了一種新的思路和方法。

2) 通過Copula函數得到的渡槽地震易損性曲線與1階界限法相比較，發現其位于1階界限法的上下界之間，表明渡槽系統的易損性大于單個構件的易損性。通過1階界限法得到的系統易損性曲線，上下界最大偏差分別為26.1%，27.0%，26.8%和26.2%，上下界帶寬較大。如果單純采用構件易損性作為渡槽整體的易損性會導致較大誤差。

3) 本研究采用的是二維Copula函數來描述渡槽排架和橡膠支座的易損性曲線。將二維Copula函數擴展為多維Copula函數，從而構造多元混合Copula函數描述多個構件的相關性，以便對更復雜的系統進行相關性分析，需要進一步研究，可以嘗試選用其他對隨機變量之間尾部相關關系變化較為敏感的Copula函數。

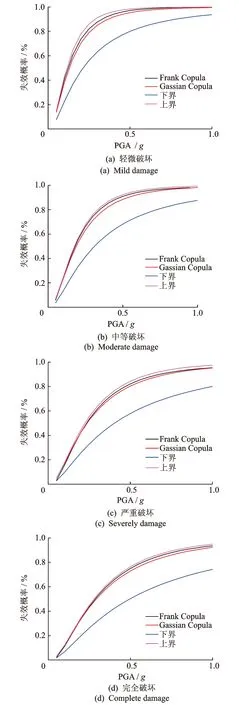
圖6 渡槽系統易損性曲線