諧波驅動柔性臂系統耦合動力學建模及辨識*

婁軍強， 周優鵬， 張振振， 陳特歡， 楊依領， 魏燕定

(1.寧波大學機械工程與力學學院 寧波，315211) (2. 浙江大學現代制造工程研究所 杭州，310027)

引 言

隨著空間技術與現代工業技術的發展，柔性機械臂及柔性臂機器人已廣泛應用于航天器、工業高端裝備以及醫療器械中[1-2]。為了滿足高精度及高平穩性的操作任務需求，柔性臂機器人的驅動部分一般采取諧波傳動方式[3]，由伺服電機和諧波減速器組成的諧波驅動關節進行驅動，具有質量輕、動態特性好、傳動比大且傳動平穩等優點[4]。諧波驅動的柔性臂機器人系統的驅動控制技術是目前柔性臂機器人領域內的研究熱點，引起了廣泛關注。

柔性機械臂系統的剛柔耦合特性導致柔性臂在運動過程中必然會產生彈性振動，柔性臂末端操作對象的運動實質上是系統剛體大位移和彈性小變形之間的慣性耦合[5]，而諧波驅動環節的引入進一步加劇了系統動力學特性的復雜性[6]。為了提高柔性機械臂末端的操作精度和指向精度，諧波驅動的柔性臂系統的動力學建模及其振動抑制問題成為了當前柔性臂機器人領域極為重要的研究課題[7]。建立精確合理的系統動力學模型是實現柔性臂系統精密驅動控制的前提和基礎。但是目前關于運動過程中的柔性臂動力學特性研究中，大多僅考慮了系統的機械特性，重點放在了柔性臂振動模型的研究上[8]，對諧波關節的驅動特性及二者之間的耦合關系則相對較少涉及。Feiliu-Talgon等[9]利用建立的柔性臂集中質量模型，分析了柔性臂的振動特性和電機驅動力矩之間的關系。Sharma等[10]基于平均自回歸滑動模型(auto-regressive moving average exogenous, 簡稱ARMAX)模型，建立了從驅動關節輸出力矩到柔性臂振動加速度的傳遞函數模型。由于諧波減速器和伺服電機組成的諧波傳動關節中摩擦、間隙及非線性等特性的存在，廖洪波等[11]基于LuGre摩擦模型研究了直流伺服電機的摩擦特性。總之，對諧波驅動的柔性臂系統的動力學特性研究，應當研究諧波驅動關節驅動特性基礎之上的柔性機械臂的運動及振動特性[12]。特別是考慮到諧波減速器傳動間隙、電機的機電耦合特性以及摩擦力的存在，如何建立諧波驅動的柔性臂系統的耦合動力學模型，并對其關鍵參數進行實驗辨識，是掌握系統耦合動力學特性的關鍵，也是實現柔性臂末端精確定位的基礎前提。

筆者研究了諧波驅動的柔性機械臂系統耦合動力學建模及參數辨識問題，在考慮摩擦特性的基礎上，通過偽隨機二進制的激勵，建立了虛擬力矩與電機轉動角位移之間的傳遞函數模型，并驗證了其正確性。分析了系統的剛柔耦合特性，從實驗辨識的角度出發，建立了系統較為準確的傳遞函數模型，為諧波驅動的柔性機械臂系統的建模提供了借鑒。

1 系統描述

本研究所涉及的對象為一端通過剛性結構夾持在諧波驅動關節上方、另一端懸置的柔性機械臂結構，其結構示意圖如圖1所示。諧波驅動關節由直流伺服電機和諧波減速器組成，其中電機型號為Maxon-EC-60，功率為400 W，額定轉速為2 680 r/min。諧波減速器為Harmonic Drive 生產的高精度輕型減速器，減速比為1∶50，型號為CSF-20-50-2UH-LW-SP。諧波驅動柔性臂系統參數見表1。

整個裝置的實物圖如圖2所示。其控制及測試流程是PC機在LabVIEW控制平臺下發出驅動控制信號，經A/D采集板卡輸出端傳輸到伺服電機控制器，伺服電機在驅動信號下轉動。電機自身帶有的增量式光電編碼器和霍爾傳感器用于實時測量電機在運動過程中的速度、位置以及電流數據。系統的剛柔耦合作用使得夾持在諧波關節上方的柔性臂會產生振動，黏貼在柔性臂根部的應變片傳感器組成的全橋電路用于檢測柔性臂的振動信息，并由動態應變儀將所測的應變量轉換為電壓量傳輸到A/D采集板輸入端，所有測量數據均輸回到LabVIEW平臺。

表1 柔性機械臂系統參數值

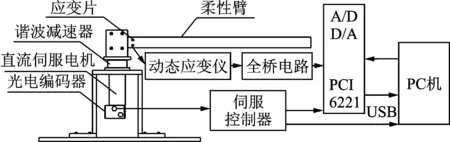
圖1 柔性機械臂系統結構示意圖

圖2 諧波驅動的柔性機械臂實驗裝置圖

2 諧波驅動模型的建立及辨識

2.1 系統驅動模型的建立及辨識

根據牛頓力學原理，整個諧波驅動柔性臂系統的力矩平衡方程可以建立如下

(1)

由于摩擦力矩Гf是影響伺服電機驅動精度的關鍵因素，所以建立適當的摩擦模型十分重要。在現有摩擦模型中，黏性摩擦力加庫倫摩擦力是應用最為廣泛的模型，其表達式[13]為

(2)

Гk的表達式為

(3)

其中：Гc為未知的庫倫摩擦力矩常數。

由式(3)可知，當電機在同一方向做勻速運動時，電機的庫倫摩擦力矩為定值。

電機的摩擦力矩項主要取決于伺服電機的轉動角速度以及庫侖摩擦力。當電機轉速較低時，電機的輸出力矩主要用于克服庫侖摩擦力。所以在實驗中為了辨識得到庫侖摩擦力矩Гc，驅動電機以1 rad/s的速度正反向勻速轉動10 s，通過多次實驗并讀取電機運行過程中電流值的方式獲得了庫倫摩擦力矩。實驗結果如表2所示，由表中數據可知，多次實驗獲得的電流值大小基本吻合。伺服電機用于克服庫倫摩擦力矩，對應的電流值為425 mA。

表2 低速轉動時的電流值

為了驗證得到的庫倫摩擦力矩的正確性，采用了逐級增加階躍電流的方式驅動電機，由圖3和圖4結果可以看出：當正向或反向的階躍電流值不超過420mA時，電機不會產生角位移輸出; 而當激勵電流值達到430 mA時，電機在正向和反向都有明顯的角位移輸出。此結果與低速轉動實驗獲得的425 mA電流值具有較高的一致性。根據maxon公司提供的電機轉矩系數km見表1，可以得到電機的庫倫摩擦力矩常數Гk的值為0.062 3 N·m。

圖3 正向階躍電流下的電機轉角曲線

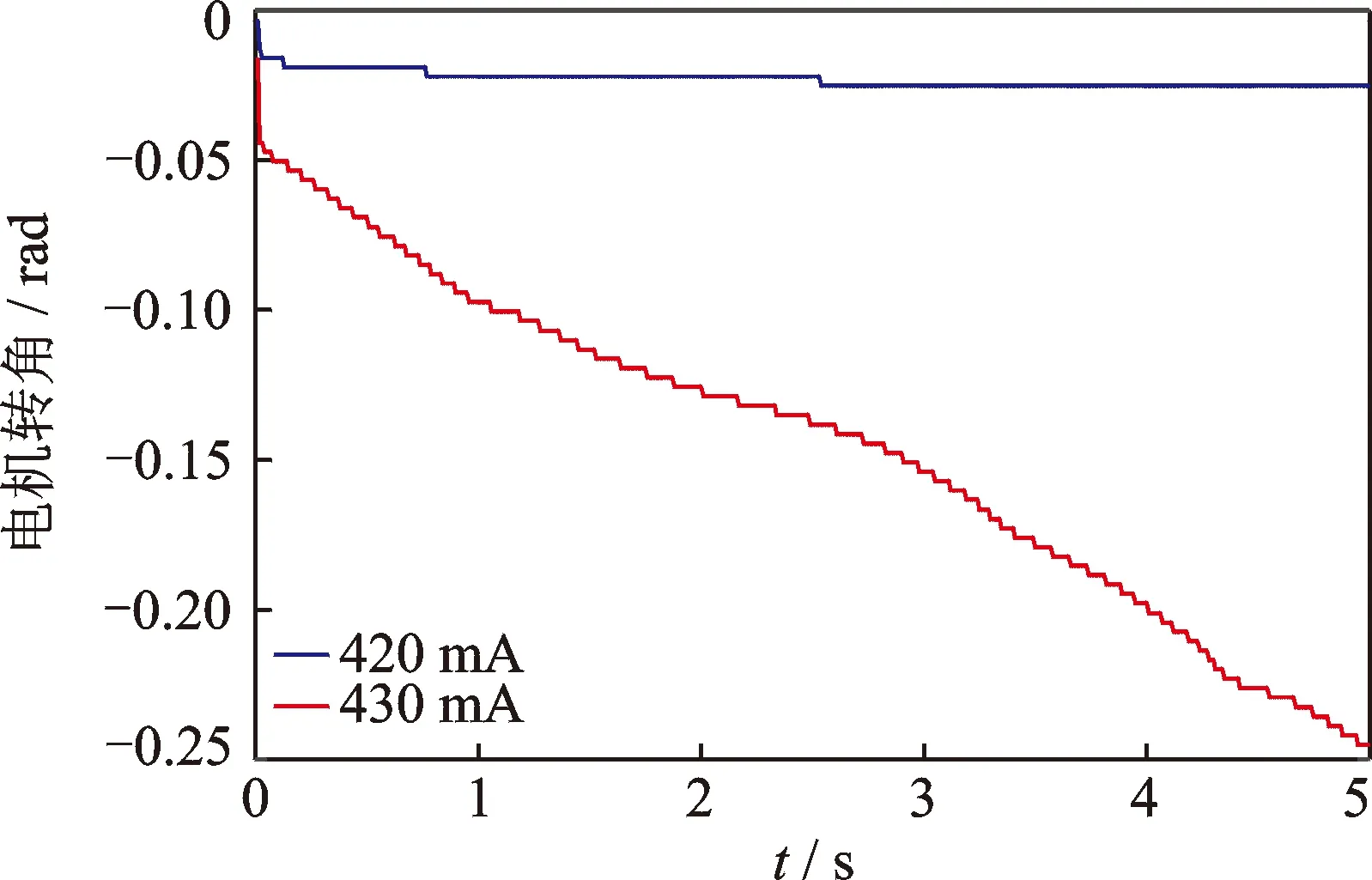
圖4 反向階躍電流下的電機轉角曲線

為了進一步辨識得到電機系統的轉動慣量J和黏性摩擦因數B，現對未攜帶柔性機械臂的系統進行研究。由于不存在柔性構件與諧波驅動關節之間耦合作用(Гcoup=0)，所以對電機驅動模型式(1)進行拉氏變換并整理得到其頻域表達式為

Γmotor(s)-ΓK(s)=Js2θ(s)+Bsθ(s)

(4)

建立諧波驅動關節的傳遞函數框圖如圖5所示。由于在電機轉動過程中，庫倫摩擦力始終與電機轉速方向相反，為非線性項，為了簡化模型，便于進行關節驅動模型辨識，現定義虛擬力矩ГE

ΓE=Γmotor-ΓK

(5)

聯立式(4)和式(5)，可得到從虛擬力矩ГE到電機轉角位移θ之間的2階傳遞函數模型

(6)

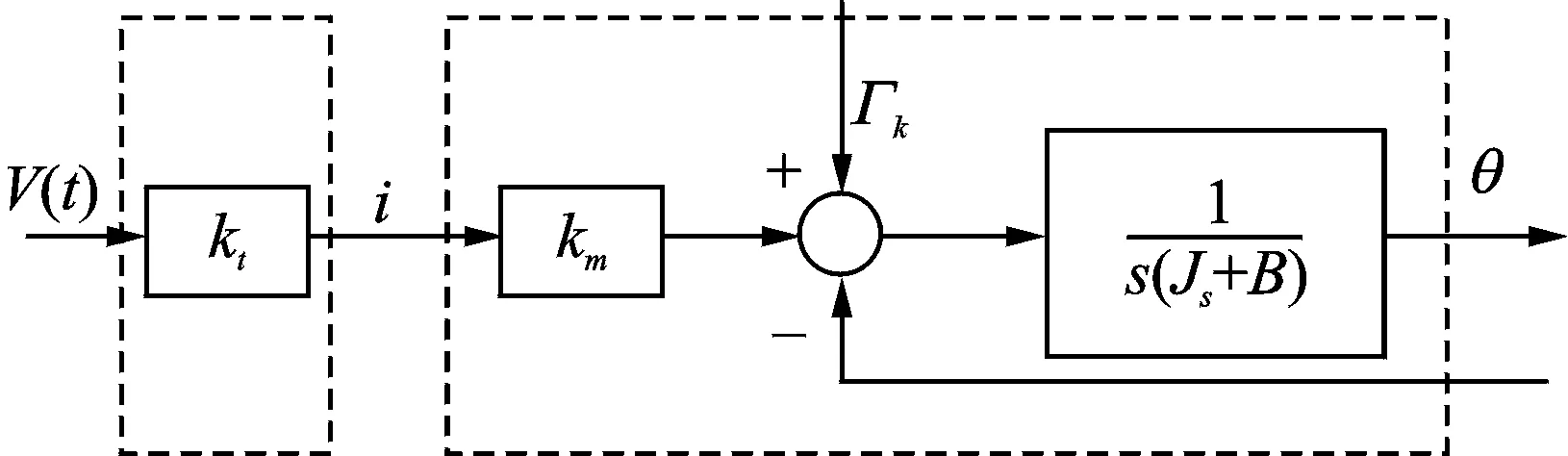
圖5 諧波驅動關節的傳遞函數框圖

系統參數的辨識精度嚴重依賴輸入信號的正確選擇。白噪聲信號作為一種理想信號，擁有均勻的功率譜，且在數學處理上具有簡單、方便等優點，所以在系統辨識和分析中占據很重要的地位。二進制偽隨機 M 序列具有近似白噪聲的性質[8]，且在工程上也易于實現，可以保證良好的辨識精度，此處選定偽隨機M序列信號作為辨識的輸入信號V(t)，如圖6所示。

圖6 二進制偽隨機M序列信號

實驗中設置伺服控制器的工作模式為電流(轉矩)模式，設置伏安轉換系數為500 mA/V，電壓輸出時間為10 s，采樣頻率為200 Hz。選擇一個幅值為1 V的二進制偽隨機M序列作為諧波驅動關節的激勵電壓信號，得到關節轉動角位移值θ如圖7所示。

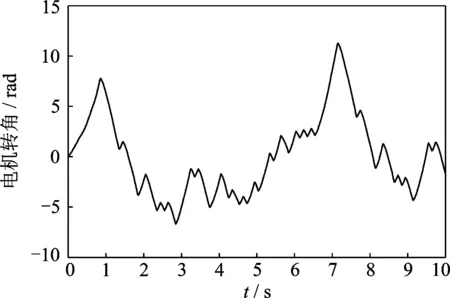
圖7 電機角位移輸出曲線

由于庫倫摩擦力矩Гk具有非線性，其方向隨著轉動角速度θ的變化而變化。為了進行系統傳遞函數辨識，需要將系統模型線性化處理，故將電機的輸出力矩在正反兩個方向同時減掉庫倫摩擦力矩，得到的虛擬力矩ГE見圖8。

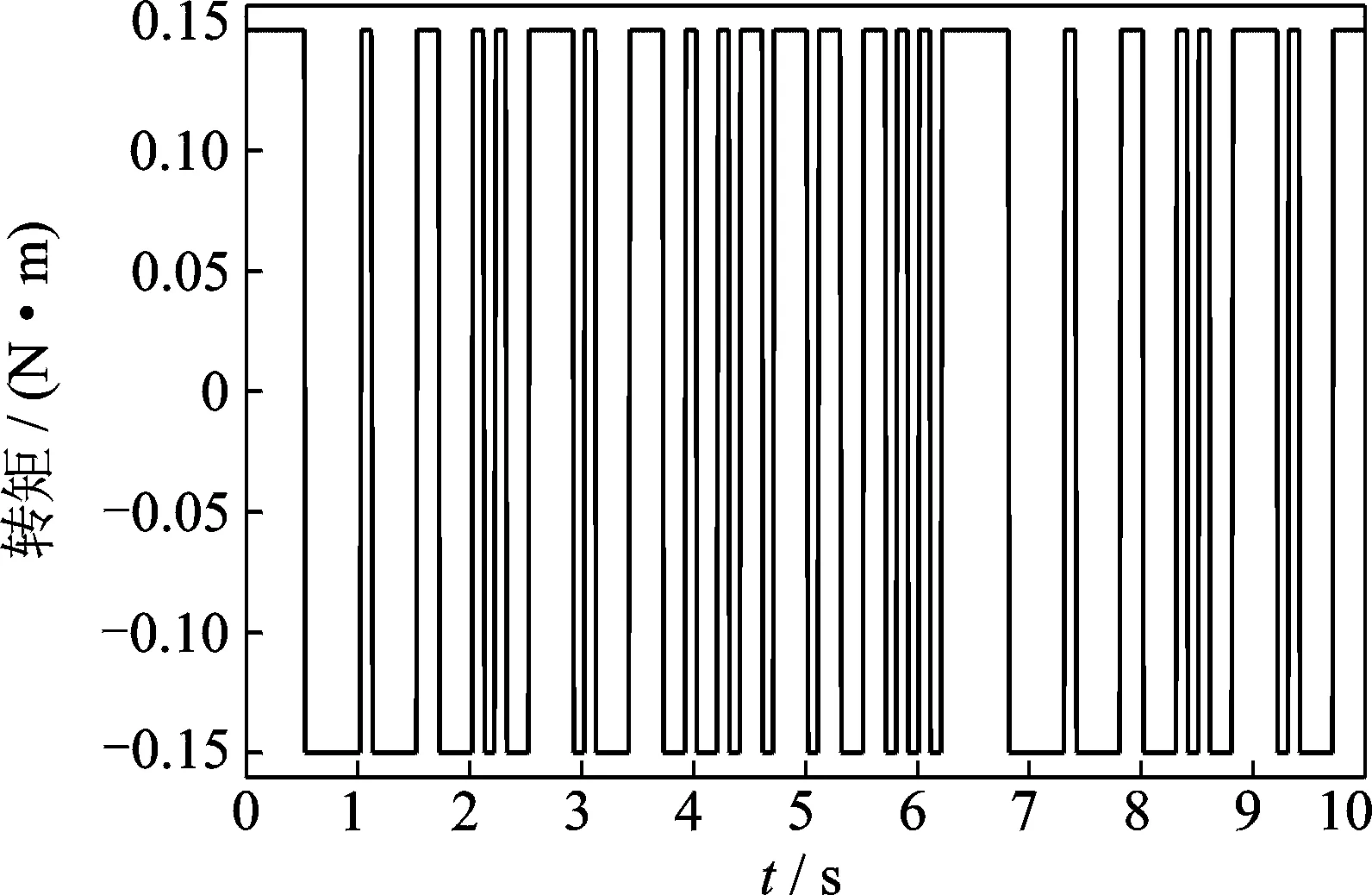
圖8 虛擬力矩值ГE

基于虛擬力矩值ГE輸入和電機轉動角位移θ輸出所建立的傳遞函數模型G(s)，并將輸入輸出信號的單位統一為標準單位之后，借助Matlab辨識工具箱進行辨識，得到其傳遞函數為

(7)

對應式(6)，忽略分母中較小的常數項，計算得到轉動慣量J為0.003 23 kg·m2, 黏滯摩擦因數B為0.007 87 (N·m)/(rad·s-1)。

圖9給出了得到的傳遞函數模型G(s)輸出與實際系統的輸出對比情況，從圖中可以看出，二者吻合較好。

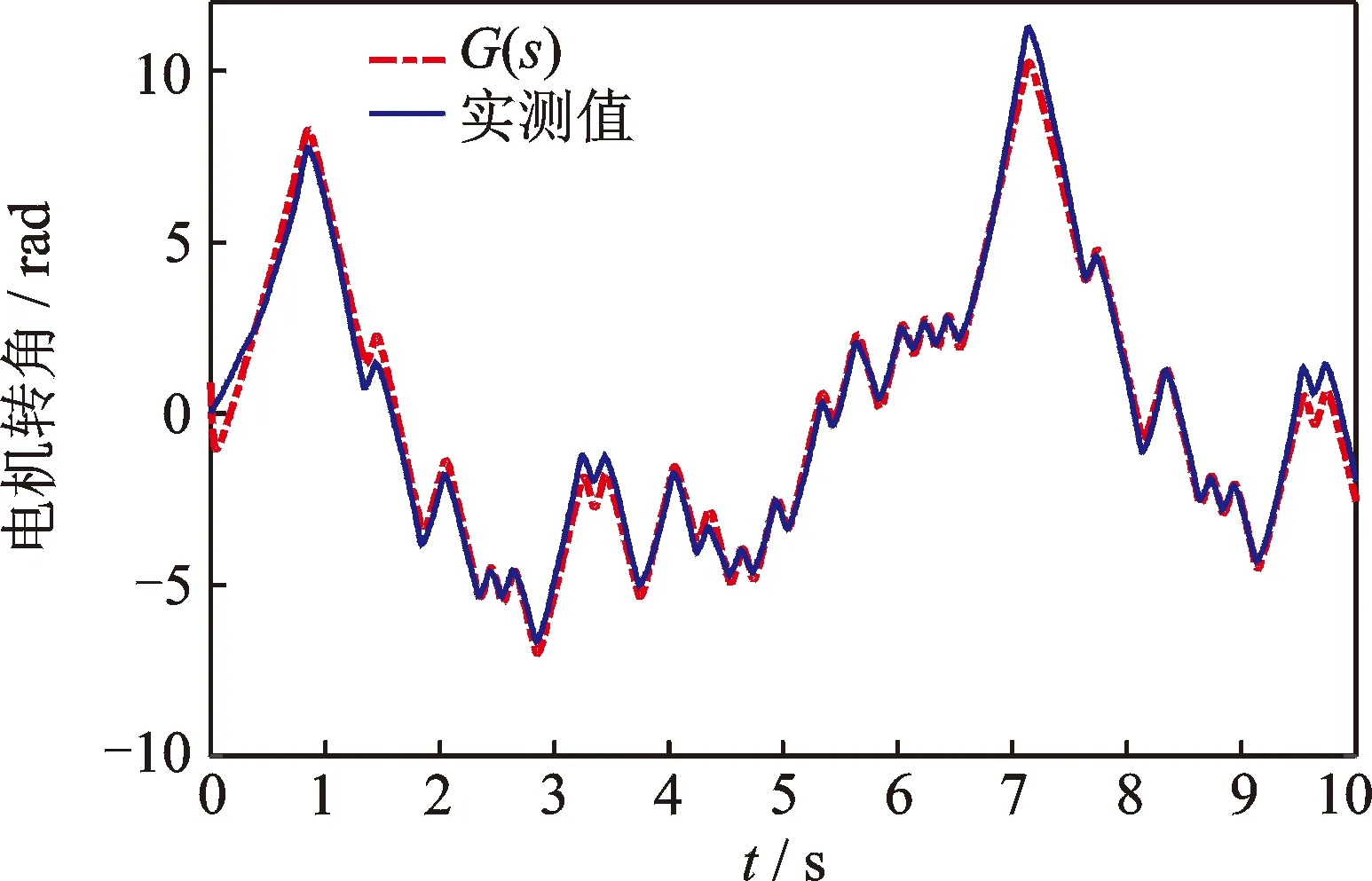
圖9 辨識模型與實際輸出比較圖

2.2 系統驅動模型驗證

為了驗證辨識得到的傳遞函數模型G(s)與實際系統的吻合程度，圖10給出了辨識模型與實際系統在另一組驅動信號激勵下的轉動角位移輸出的比對結果。

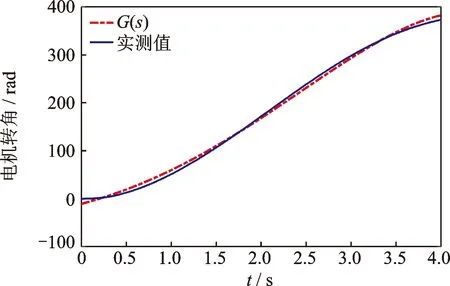
圖10 電機角位移曲線

在模型驗證實驗中，用圖11所示的三次多項式電壓信號作為電機的控制電壓信號。

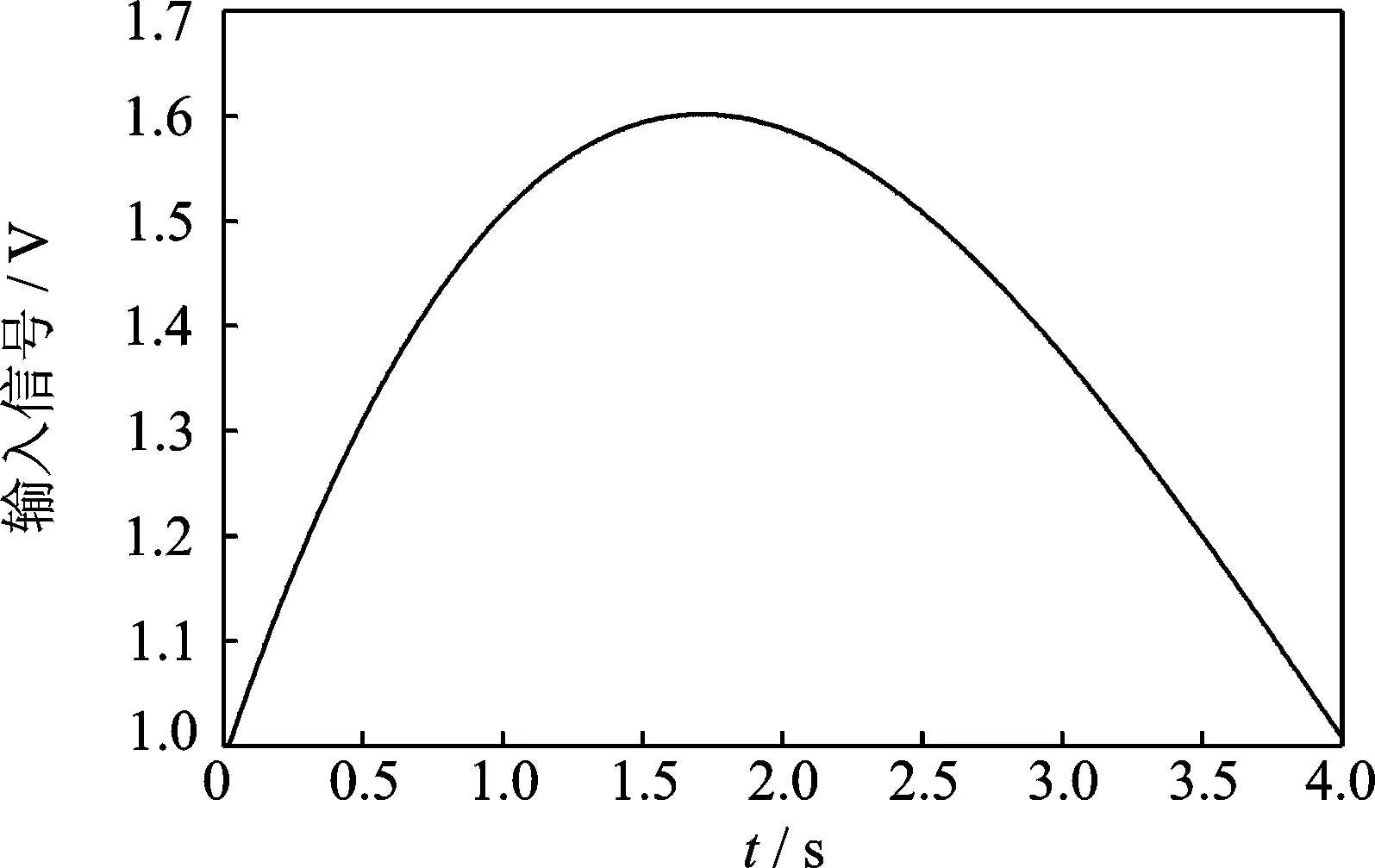
圖11 控制電壓信號

實驗結果表明，辨識得到的系統驅動模型G(s)預測的電機轉角位移與實際的電機轉角位移仍具有較高的吻合度，充分說明了辨識得到的虛擬力矩與角位移之間傳遞函數模型是有效的。

3 柔性臂振動模型辨識

3.1 諧波驅動柔性機械臂系統動力學建模

在電機轉動的激勵下，因為柔性臂的縱向振動相對于其橫向振動可以忽略不計，所以在建模過程中，只考慮柔性臂的橫向振動[14]。建立系統坐標系如圖12所示。

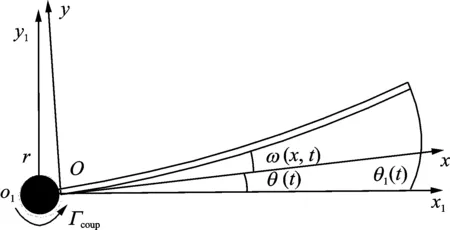
圖12 柔性臂運動坐標示意圖

圖中坐標系x1O1y1為固定慣性坐標系，坐標系xOy為固連在柔性臂根部的浮動坐標系。θ(t)為柔性臂根部的轉角，θ1(t)為柔性臂末端的轉角，w(x,t)為距離柔性臂根部x處點的彈性位移。在集中質量法的前提下，采用單個集中質量進行柔性臂的動力學模型建模，則柔性機械臂的振動模型可以表示為

(8)

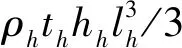
柔性臂的耦合振動力矩Гcoup表達式為

(9)

聯立式(1)、式(8)和式(10)可得包括考慮諧波的摩擦、柔性關節和柔性臂因素的理論動力學模型為

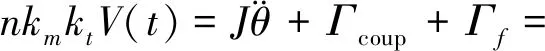
(10)

3.2 柔性臂耦合振動模型的建立及辨識

在得到了較為精確的驅動模型G(s)之后，為了獲取較為完整的諧波驅動柔性臂系統的傳遞函數，需要對系統的剛柔耦合特性進行分析。這里將進一步通過實驗辨識法建立以電機角位移θ(t)為輸入、柔性臂振動位移w(x,t)為輸出的傳遞函數模型。

由于柔性機械臂的橫向振動位移w(x,t)相對于長度lh較小，所以和末端具有如下關系

(11)

聯立式(9)和式(11)，得到振動耦合力矩Гcoup為

(12)

柔性臂的應變信號εa通過應變全橋電路和動態應變儀的調理后，將應變量轉化為電壓量，輸出電壓信號為Vt

(13)

其中：S1為應變片傳感器的靈敏度系數；U0為全橋電路的供電電壓；w″(0,t)為柔性臂根部振動位移關于位置變量x的2階偏導數。

在小彈性變形的假設前提下，柔性臂的根部應變與末端應變具有線性變換關系，結合式(13)可得

(14)

其中：為柔性臂根部與末端應變之間的線性變換系數。

聯立式(14)和式(15)，得到應變全橋電路的輸出電壓Vt與耦合振動力矩Гcoup具有如下線性關系

(15)

振動耦合力矩Гcoup和轉動角位移θ之間的傳遞函數模型H(s)[10]為

(16)

其中：ξi為第i階振動模態阻尼；ωi為第i階振動模態的角頻率。

由于振動耦合力矩Гcoup(t)和應變輸出電壓Vt(t)是線性關系， 結合式(15)和式(16)，得到電機轉動角位移θ(t)和Vt(t)之間的傳遞函數H(s)

(17)

圖13給出了動態應變儀和全橋電路檢測到柔性臂的應變輸出電壓Vt(t)。根據式(17)，以圖7所示電機角位移θ(t)為輸入，圖13應變電壓輸出Vt(t)作為輸出，通過Matlab系統辨識工具箱對輸入輸出實驗數據進行傳遞函數模型辨識。

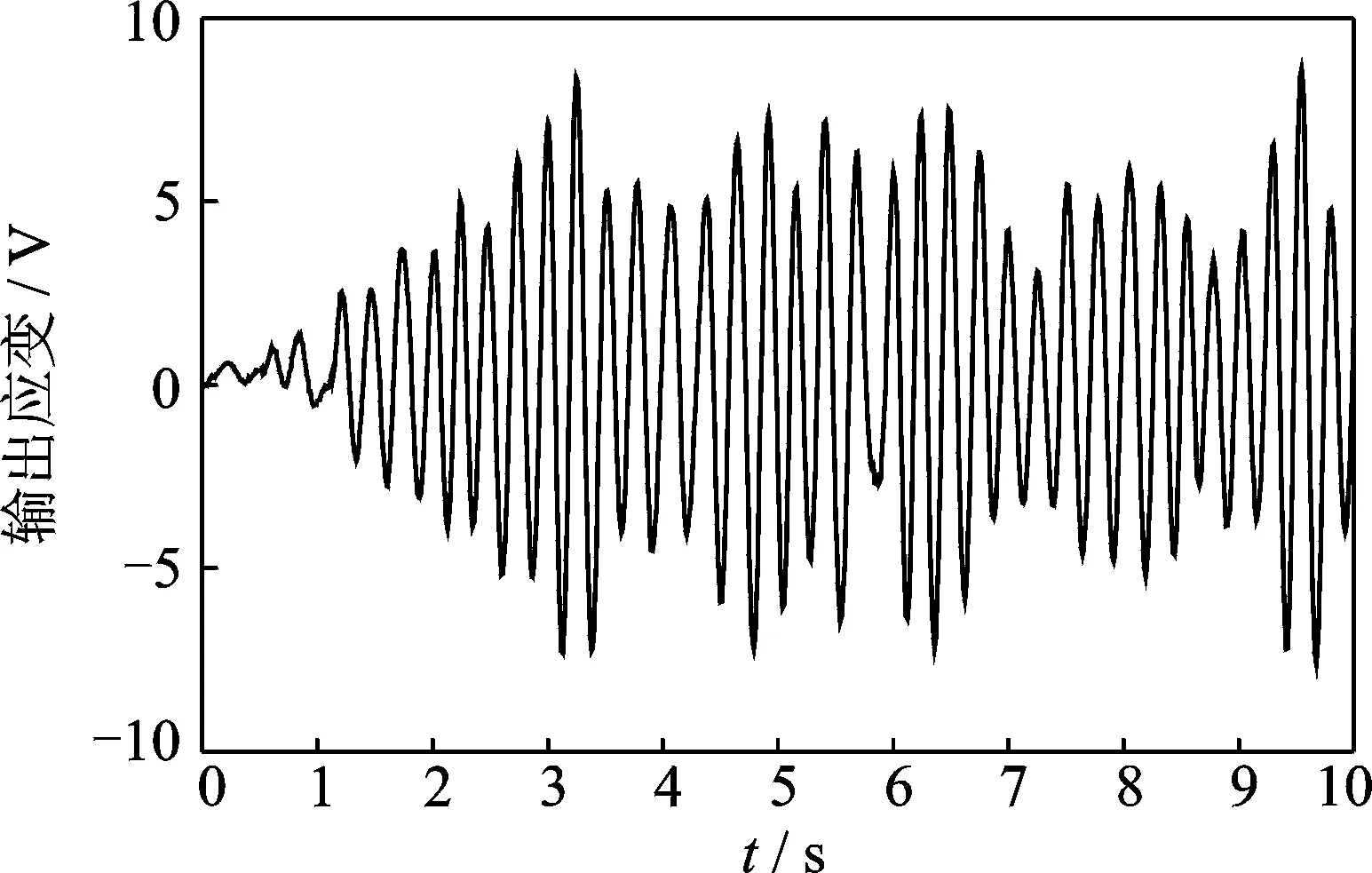
圖13 應變電壓輸出

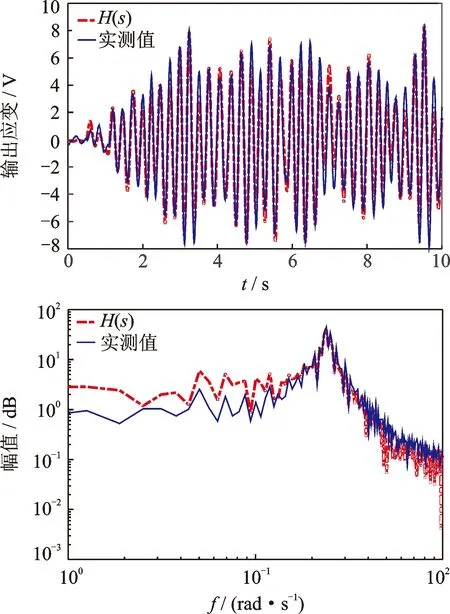
圖14 辨識模型H(s)與實際結果時域和頻域比較圖

圖14給出了辨識模型H(s)的預測輸出與實際結構輸出的時頻域對比結果。從結果可以看出，此模型與系統實測數據基本吻合，雖然辨識出的頻域曲線在0～10rad/s的低頻域區間與系統響應存在著一定程度的失真，但是在1階固有頻率處較好地契合了柔性臂的實際頻率響應。該時頻域擬合曲線的整體趨勢均能夠反映辨識模型的準確性。在柔性臂1階振動模態占主導的情況下，此處僅截取柔性臂的1階振動模型進行傳遞函數辨識，辨識得到柔性臂的1階固有頻率為3.8 Hz(23.85 rad/s)。其傳遞函數H(s)為

(18)

與式(17)相對應，計算得到柔性臂的振動頻率ωi為23.13 rad/s(3.8 Hz)，振動模態阻尼ξi為0.006 25。

3.3 柔性臂耦合振動模型驗證

為了進一步驗證辨識得到傳遞函數模型對于實際系統的匹配程度，實驗中通過一個梯形電壓控制下的角位移θ(t)作為輸入，應變片輸出電壓Vt(t)作為輸出進行模型驗證。

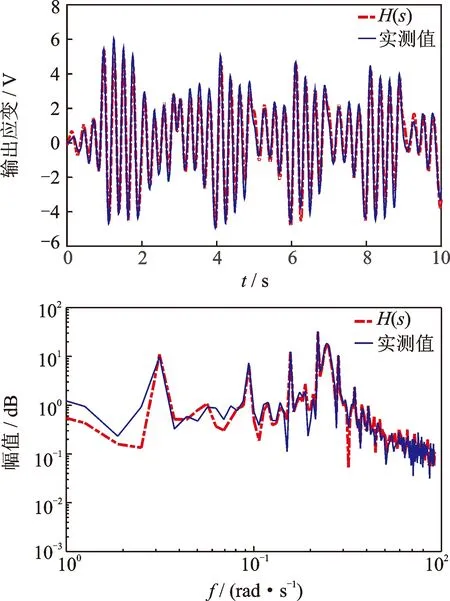
圖15 辨識模型H(s)與實際結果驗證比較圖

圖15給出了辨識模型與實際結果在時域和頻域的輸出對比結果，由于存在著一定的測量誤差和噪聲誤差，模型和實驗結果并非完全一致，但是整體趨勢基本上能夠反映系統的振動特性。從頻域信號來看，雖然辨識模型H(s)與實際結構低頻域區間內的響應特性具有一定的差異，存在著一定程度的失真，導致辨識模型H(s)的辨識精度下降，但是H(s)在固有頻率附近處與實際結構的頻率響應基本重合，較高精度地刻畫了柔性臂在伺服關節驅動下的1階振動特性，這充分證明了此得到的傳遞函數模型H(s)對于實際系統的有效性。

表3給出了辨識得到的兩個傳遞函數模型H(s)和G(s)與實際系統的吻合率，更加直觀地說明了辨識結果的正確性。

表3 模型吻合度指標計算表

4 結束語

以諧波驅動柔性臂系統的耦合動力學建模及辨識為研究背景，分析了諧波關節的驅動及摩擦特性，并通過實驗辨識法得到了其關鍵參數。分析了系統的剛柔耦合特性，通過實驗辨識方法建立了伺服電機轉動角位移和柔性臂耦合振動力矩之間的傳遞函數模型。實驗結果表明，辨識得到的模型輸出與實際結構具有較高的一致性，說明了此辨識方法的可行性。本研究從實驗辨識的角度出發，建立了系統較為準確的傳遞函數模型，為諧波驅動的柔性機械臂系統的建模提供了借鑒。