基于顆粒阻尼器的曲線橋減震分析與試驗*

2019-12-31 01:07:24許維炳閆維明何浩祥陳彥江

振動、測試與診斷 2019年6期

許維炳，閆維明，何浩祥，陳彥江

(北京工業大學工程抗震與結構診治北京市重點實驗室北京，100124)

引言

曲線橋對空間和線形均有良好的適應性，因此在地形復雜的公路、山區道路及空間受限的城市高架橋中有著廣泛的應用[1]。受場地、施工、經濟投入等因素的影響，小半徑曲線橋(曲率半徑<100 m)也在很多工程中出現[2]。由于曲率半徑的影響，曲線橋的彎扭耦合作用是其不同于直線橋的重要特性。受彎扭耦合作用以及復雜地質條件下近端層地震大脈沖作用等不利因素的影響，曲線橋(特別是小半徑曲線橋)在地震中的損壞、垮塌現象較多，例如汶川地震中的百花大橋、回瀾立交匝道橋等[3-4]。

鑒于曲線橋多位于公路交通和城市交通的節點位置，國內外學者針對曲線橋的減震控制開展了大量工作。總結國內外文獻[5-12]，曲線橋減震控制研究成果主要集中于耗能支座、隔震支座、黏滯阻尼器以及半主動控制裝置等耗能減震裝置的應用可行性分析和效果研究。相關成果存在的問題主要有：a.缺少相關的大比例尺振動臺試驗驗證；b.由于曲線橋曲率半徑的影響(彎扭耦合效應)和地震作用方向的不確定性，上述減震器的控制效果的方向性較為顯著。因此，提出適用于曲線橋的新型減震裝置并開展相關的振動臺驗證試驗具有重要的科研和工程實用價值。

顆粒阻尼技術是將阻尼顆粒按一定填充率放置于結構內部或結構附屬空腔內，當受控結構振動時，顆粒之間、顆粒與腔體之間將不斷地碰撞和摩擦，不但有動量交換，而且能夠耗散系統的振動能量，藉此達到減輕結構振動的目的，其具有減震效果好、布置靈活等優點[13-16]。通過設計顆粒填充率來調整顆粒阻尼器中顆粒的堆積狀態，當顆粒不發生堆積時，阻尼顆粒理論上可沿各個方向在阻尼器腔體自由運動，設計合理的顆粒阻尼器對結構的控制效果受地震方向和結構振動形態(存在彎扭耦合作用)的影響較小。顆粒阻尼器在直線梁橋、長周期大跨橋梁減震控制中均取得了較好的效果[17-18]，因此，筆者以某典型的曲線橋為研究對象，設計制作了該橋的1/10縮尺試驗模型及適用于該縮尺模型橋的CPD，通過對附加CPD前后的曲線橋縮尺模型振動臺試驗，重點分析了不同地震波類型(遠場地震波、近斷層地震波)和不同激勵方向(順橋向、橫橋向)等條件下CPD對曲線橋的控制效果，為顆粒阻尼技術在曲線橋減震控制中的應用及解決傳統消能減震裝置在曲線橋中的減震效果方向性提供借鑒。試驗在北京工業大學工程抗震與結構診治北京市重點實驗室9子振動臺臺陣系統上開展。

1 曲線橋模型橋試驗設計

選取某典型的曲線連續梁橋作為設計原型橋，原型橋中心線跨徑布置為4×40 m，全長為160 m。上部結構為單箱三室鋼筋混凝土箱梁，下部結構為鋼筋混凝土雙柱式橋墩。橋梁中間橋墩(3#)和主梁采用固定支座連接，其余各墩(1#，2#，4#，5#)與主梁均采用沿橋梁軸線方向可以滑動的單向滑動支座連接，橋梁中心線曲率半徑為102.55 m，全橋圓心角為92°。

1.1 模型橋設計

綜合考慮振動臺的技術參數和動力試驗結果的有效性，對原型橋采用1/10比例進行縮尺，并依據相似理論[19]確定試驗模型的主要動、靜力相似系數，如表1所示。

表1 相似特性

1.1.1 上部結構

地震作用下，橋梁上部結構除發生碰撞或落梁引起的構件破壞外，基本不發生塑性破壞[2-3]。為減少施工周期和方便加工，模型橋上部結構采用剛度相似原理等效設計，而不過分追求截面形式一致，模型橋主梁設計時使用Qd345鋼材代替原型橋的混凝土材料。

1.1.2 下部結構

下部結構是模型橋與原型橋靜動力參數相似的關鍵，模型橋下部橋墩與原型橋下部橋墩需嚴格滿足相似關系。模型橋橋墩的受力鋼筋與原型橋材料相同，配筋面積滿足相似原理，2#～4#橋墩主筋選用8根等級為HRB335Φ10的鋼筋，1#和5#橋墩主筋選用12根等級為HRB335Φ10的鋼筋，橋墩主筋均等分橋墩截面均勻布置于橋墩內，箍筋采用等級為HPB235Φ6的鋼筋，按0.10 m間隔布設，滿足最小配筋率和配箍率要求。模型橋主要構件選材和設計參數如表2所示。

1.1.3 支撐系統

原型橋中1#，2#，4#和5#橋墩的支座系統采用單向滑動盆式橡膠支座，3#墩采用固定盆式橡膠支座。模型橋支座系統的設計很難做到嚴格按照原型橋進行縮尺。模型橋中1#，2#，4#和5#橋墩的支座系統采用GPZ(II)0.8DX單向滑動盆式橡膠支座進行模擬，3#墩選取GPZ(II)0.8GD固定支座進行模擬。

表2 試驗模型主要構件設計參數

1.2 配重設計

原型橋1#～3#橋墩的軸壓比分別為0.04，0.16和0.14，為使模型橋的破壞模式以及發生破壞的條件與原橋相似，同時避免由于動力相似比例過小而造成試驗地震波持時過短，試驗中沿橋跨方向均勻布置約7.0t的配重塊，配重后1#～3#橋墩軸壓比分別為0.02，0.08和0.07。模型橋如圖1所示。

圖1 模型橋整體布置

1.3 模型橋基本動力參數識別

為獲取模型橋基本動力特性和模擬地震響應，分別在橋墩和主梁的徑向(沿圓心半徑方向)和切向(垂直于半徑方向)布置加速度傳感器和位移傳感器。同時為了對輸入地震波的有效性進行控制，在橋墩底部振動臺臺面也設置了沿徑向和切向的加速度傳感器。

地震模擬振動臺試驗前，分別沿順橋向和橫橋向(順橋向為1#，5#墩連線方向；橫橋向為垂直于1#，5#墩連線方向)輸入白噪聲激勵，以分析模型橋系統的基本動力特性。圖2給出了白噪聲激勵下3#墩墩頂加速度響應的自功率譜曲線。

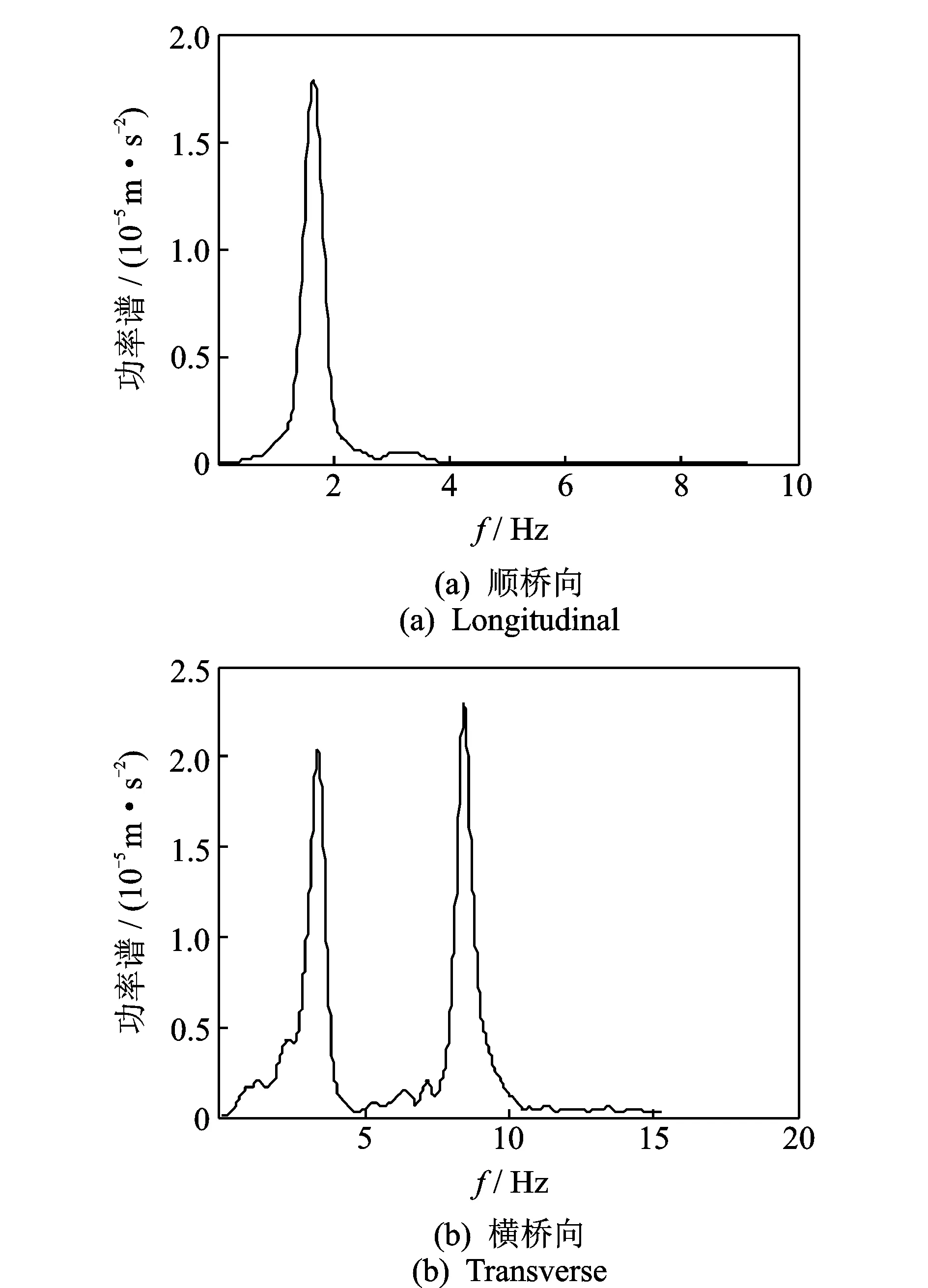
圖2 白噪聲激勵下3#墩墩頂加速度響應自功率譜曲線

由圖2可知，模型橋沿順橋向的振動以順橋向1階振型振動為主，順橋向1階自振頻率約為1.64 Hz；模型橋在橫橋向的振動則主要包含2階振型，橫橋向1階自振頻率為3.39 Hz，2階振動頻率為8.44 Hz。利用MIDAS Civil軟件建立模型橋的數值分析模型，模型橋的基本動力特性數值分析結果與試驗結果統計見表3。

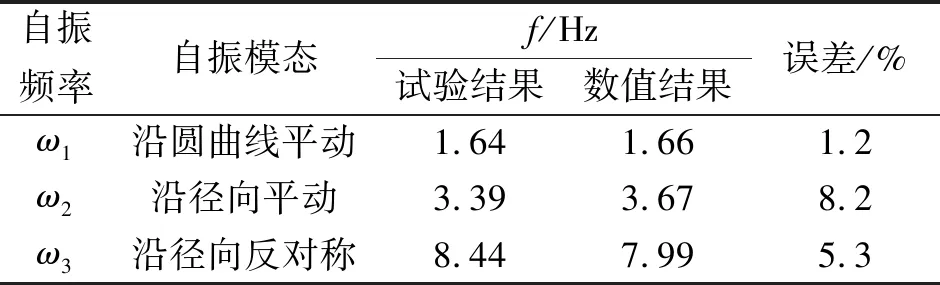
表3 模型橋自振特性

由表3可知，模型橋的有限元分析結果的前3階自振頻率與模型橋實測數據基本一致，設計模型與制作模型吻合良好，模型橋系統和測試傳感器的狀況良好。

1.4 地震波選取

1.4.1 遠場地震波

不失一般性，針對原型橋所在地的地質條件(Ⅱ類場地)依據橋梁抗震設計規范選取了3條遠場地震波，分別為El-Centro波、Chi-Chi波，以及依據規范反應譜理論[20]設計的1條人工波進行振動臺試驗，以驗證CPD在遠場地震波作用下對曲線橋的減震效果。

1.4.2 近斷層地震波

作為與遠場地震波的對比，針對原型橋所在地的地質條件依據PEER-NGA地震波的選波過程選取了3條II類場地近斷層地震波(PEER分類C類場地)。圖3給出了試驗中選取的3條II類場地近斷層地震波反應譜曲線與目標反應譜曲線。

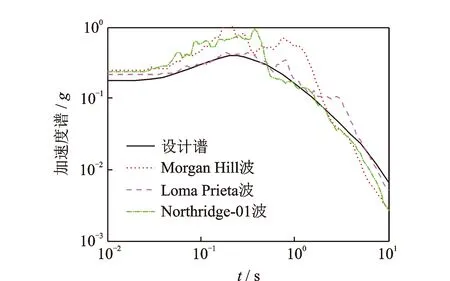
圖3 近斷層地震波設計反應譜與選取地震波反應譜曲線

由圖3可知，依據PEER-NGA選取的近斷層地震波反應譜與設計反應譜在0.01～10 s周期內的譜值基本一致，近斷層地震波在長周期上均有一定的大脈沖效應。

1.5 顆粒阻尼器設計

考慮到曲線橋彎扭耦合效應對減震裝置減震效果方向性的影響，以及土木工程領域受控結構響應的低頻、低幅特性，筆者提出一種阻尼器腔體與受控曲線橋剛接，腔體內阻尼顆粒不發生堆積，在各個方向均有較優減震控制效果的顆粒阻尼器——曲型艙顆粒阻尼器，如圖4所示，CPD包括阻尼器腔體、阻尼器與受控結構連接件(剛度為K)和阻尼顆粒。

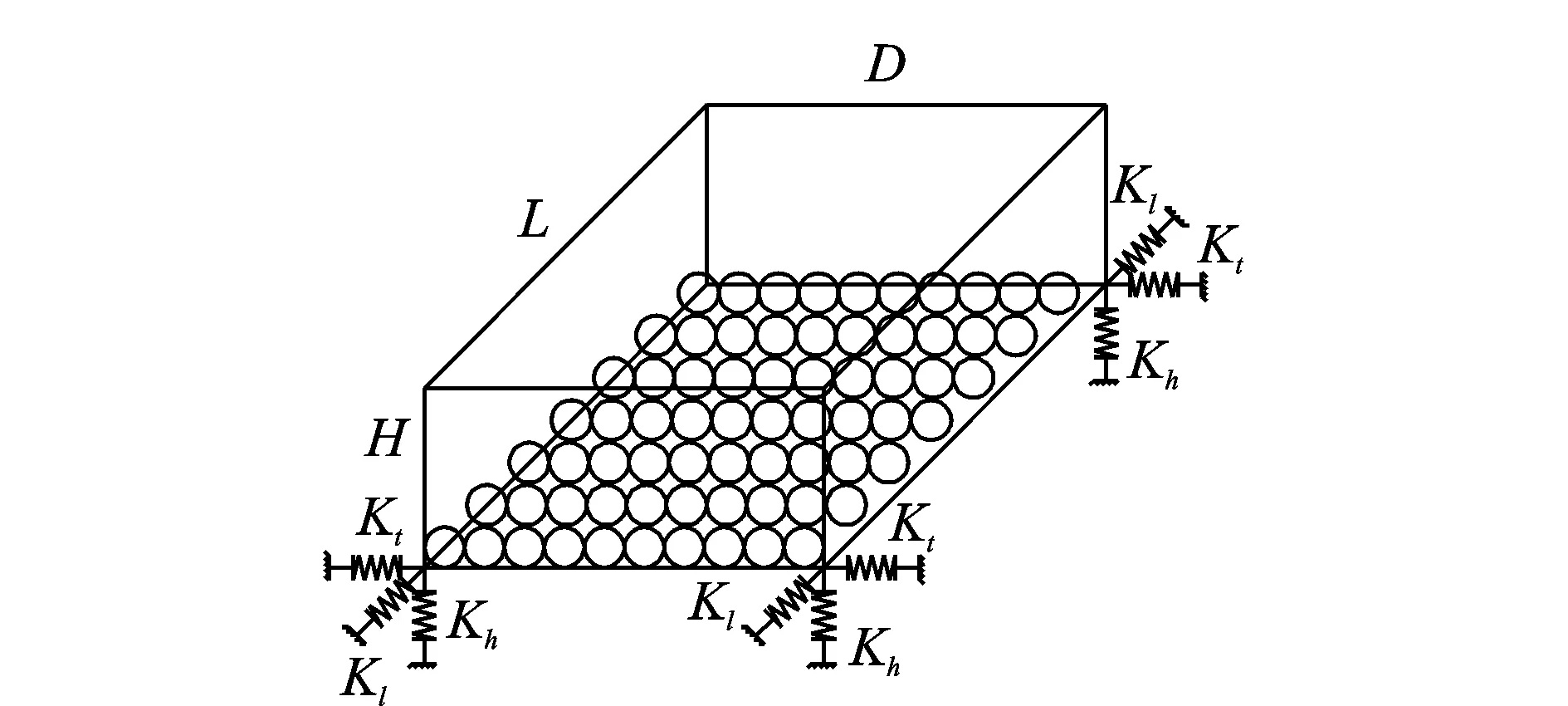
圖4 CPD模型

考慮到土木工程結構振動的低頻、低幅特點，顆粒阻尼器在土木工程結構中的減震效果主要是調諧作用和摩擦碰撞耗能作用，而調諧作用占主導[21]。為了提高CPD的調諧作用，應避免顆粒在阻尼器腔體中發生堆積，當顆粒不堆積或者堆積高度較小時，CPD腔體的設計參數[22]可由下式計算確定

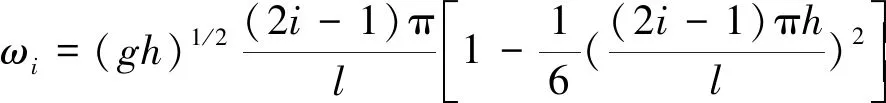
(1)

其中：ωi為受控結構的第i階自振頻率；g為重力加速度；h為顆粒堆積高度；l為阻尼器腔體在結構第i階陣型振動方向上的長度。

CPD在曲線橋中應用的設計流程為：

1) 設計與曲線橋中心線曲率半徑相同的阻尼器腔體，腔體的尺寸分別依據式(1)和受控橋梁的縱、橫橋向1階振型頻率確定；

2) 沿橋跨方向均勻布置阻尼器腔體(試驗模型橋均勻布置了4個阻尼器腔體)；

3) 阻尼器腔體與主梁的預置鋼構件焊接連接(原橋設置于箱梁內，模型橋設置于橋面上)；

4) 阻尼器腔體中按一定的填充率設置阻尼顆粒(阻尼顆粒的基本設計參數依據淺水振動方程確定[22]，以不發生堆積為宜確定最大附加質量比)。

依據上述設計流程，試驗模型橋用CPD的整體布置如圖5所示。

圖5 阻尼器布置圖

為避免結構出現安全隱患，并使阻尼顆粒不發生堆積，以增強阻尼器在不同方向的效果，同時為了使阻尼顆粒與腔體之間能夠發生碰撞，試驗中設置了4個阻尼器腔體，并根據顆粒附加質量的增加分別選取其中的2個、3個和4個設置阻尼顆粒。振動臺試驗中選取的阻尼顆粒附加質量、材料、腔體尺寸等參數見表4。為發揮分布式阻尼的特點，CPD-1在2#～4#墩之間兩跨的阻尼器腔體中均勻布置阻尼顆粒；CPD-2在1#～4#墩之間三跨的阻尼器腔體中均勻布置阻尼顆粒；CPD-3在全橋四跨的阻尼器腔體中均勻布置阻尼顆粒。

表4 阻尼器參數

2 減震前模型橋地震響應結果

為了有效評價臺面輸入與墩頂響應，引入有效均方根加速度和有效均方根位移作為地震動輸入和結構動力響應的衡量指標。

有效均方根加速度定義為

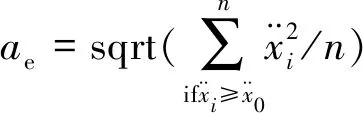
(2)

有效均方根位移定義為

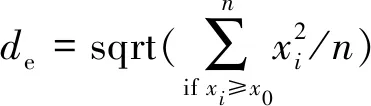
(3)

分別輸入壓縮后加速度幅值調整系數E1=90 cm/s2，E2=220 cm/s2的地震波[19](El-Centro波、Chi-Chi波、人工波和近斷層地震波)進行無阻尼器曲線模型橋的振動臺試驗。圖6給出了順橋向E1和E2作用下，模型橋3#墩墩頂順橋向位移響應時程曲線。

由圖6可知，E1和E2地震作用下，模型橋的動力響應滿足一定的比例關系。以橫橋向為例，表5給出了不同地震波橫橋向激勵下臺面響應與模型橋#3墩頂響應的關系。

由表5可知，E1和E2地震作用下，曲線模型橋臺面輸入與墩頂響應之比基本保持一致，即曲線模型橋基本處于彈性狀態。

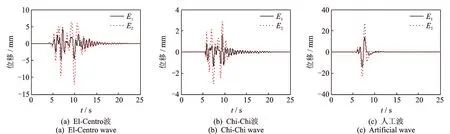
圖6 順橋向E1和E2作用下模型橋3#墩墩頂順橋向位移響應時程曲線

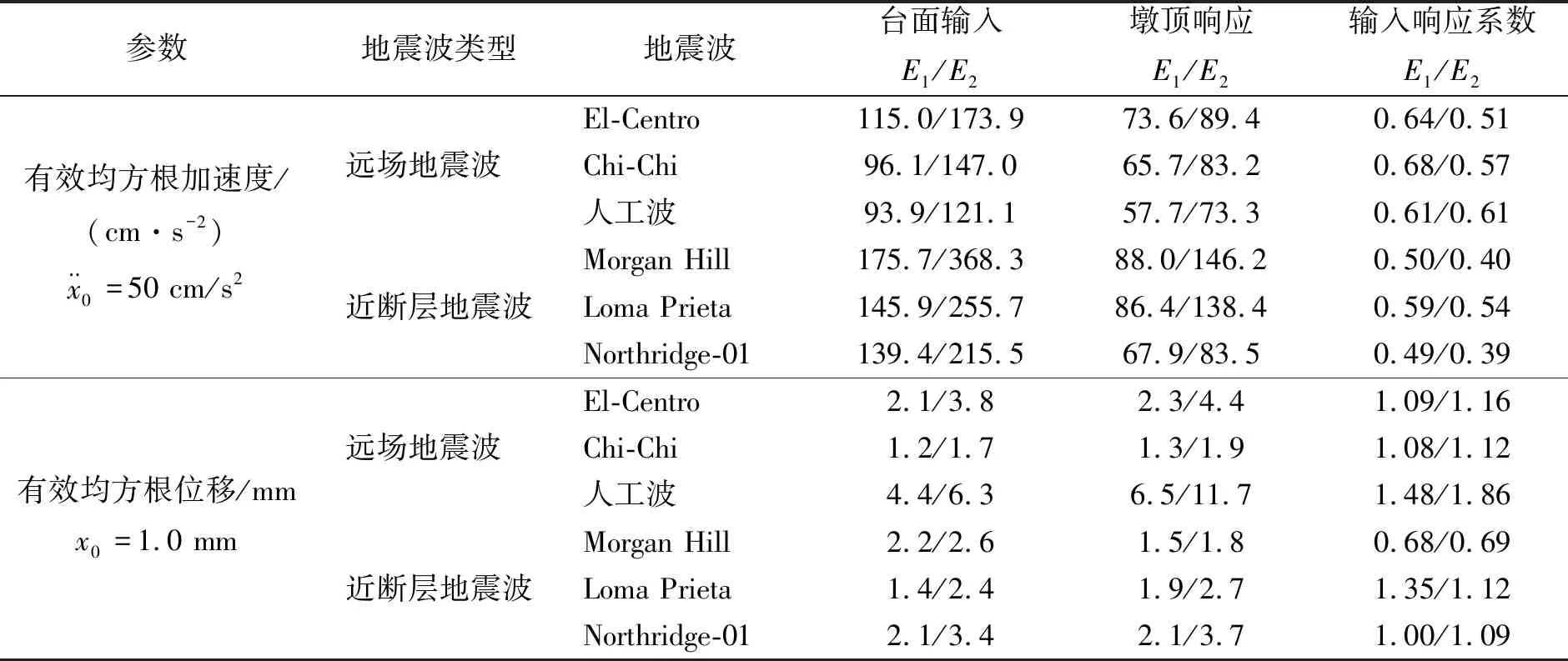
表5 模型橋3#墩臺面輸入與墩頂響應峰值統計

3 減震后模型橋地震響應結果

設定模擬地震動的加速度峰值為E1和E2，對設置不同附加質量比CPD的模型橋進行遠場地震波和近斷層地震波激勵下的振動臺試驗。為評價CPD對曲線橋不同方向激勵震動響應控制的效果，分別沿順橋向和橫橋向輸入地震波。

3.1 遠場地震波

以Chi-Chi波為例，圖7給出了順橋向E1作用下，模型橋3#墩墩頂順橋向位移響應曲線。

由圖7可知，Chi-Chi波E1沿順橋向激勵時，設置不同的CPD后，模型橋的位移響應均有一定程度的降低。模擬地震激勵剛開始時，CPD對模型橋的動力響應略有放大，激勵持續一段時間后CPD才開始發揮減震效果，這是由于顆粒阻尼器的減震效果與顆粒與腔體之間的相對運動狀態密切相關[21]。當模擬地震激勵剛開始時，顆粒與腔體之間基本保持相對靜止，阻尼器僅依靠腔體與結構之間的彈性連接提供一定的調諧作用，相當于單調諧質量阻尼器(tuned mass damper，簡稱TMD)，其減震效果受地震波影響很大[23-24]；當模擬地震動持續一段時間后，結構的動力響應增大，顆粒與腔體之間發生相對運動或碰撞，此時顆粒阻尼器不僅能夠提供更優的調諧作用，同時能夠提供一定的耗能作用，進而發揮較好的減震效果。對于土木工程結構，有效均方根加速度減震率和位移峰值減震率是關注的重點。設定對結構動力響應有明顯作用的有效加速度下限值為20 cm/s2，以3#墩為例，表6給出了遠場地震波作用下CPD的減震控制效果統計。

由表6可知，遠場地震波作用下，CPD對模型橋的順橋向和橫橋向均有一定的減震控制效果。以位移峰值減震率為例，E1地震作用下，橫橋向和順橋向CPD的最大減震率分別為15.4%和13.9%；E2地震作用下，橫橋向和順橋向CPD的最大減震率分別為16.0%和22.3%；CPD對模型橋順橋向和橫橋向均有減震效果；不同地震波作用下，CPD對模型橋的控制效果的離散性較大，這與阻尼顆粒運動的非線性有關。

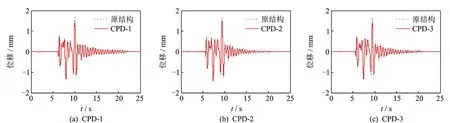
圖7 順橋向E1作用下模型橋3#墩墩頂順橋向位移響應曲線(Chi-Chi波)

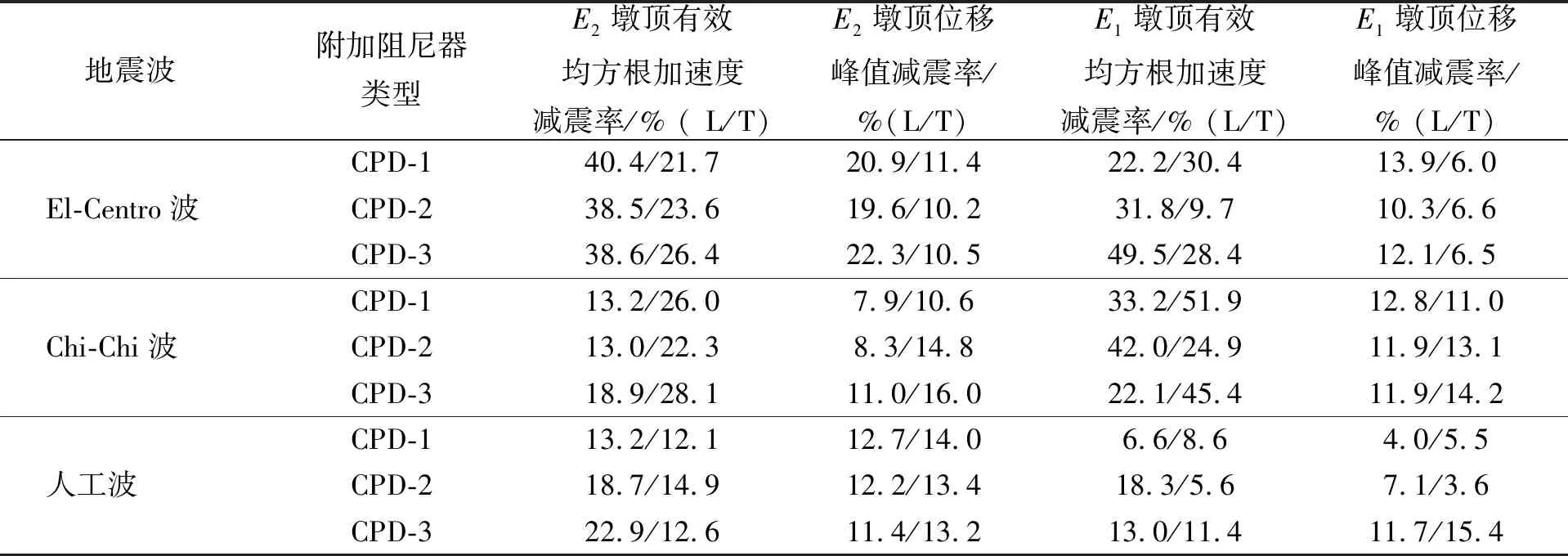
表6 遠場地震波作用下CPD減震控制效果

L表示地震波沿順橋向激勵；T表示地震波沿橫橋向激勵

3.2 近斷層地震波

以II類場地近斷層地震波Morgan Hill波為例，圖8給出了橫橋向E1作用下，模型橋3#墩墩頂橫橋向位移響應曲線。

由圖8可知，近斷層Morgan Hill波E1作用下，CPD對模型橋的墩頂位移響應具有較為顯著的控制效果。仍然設定對結構動力響應有明顯作用的有效加速度下限值為20 cm/s2，以3#墩為例，表7給出了CPD對模型橋動力響應的控制效果。

由表7可知，與遠場地震波類似，近端地震作用下CPD對模型橋的順橋向和橫橋向地震響應均有一定的抑制作用，但近斷層地震波激勵下CPD的減震控制效果受地震波影響更大。沿順橋向激勵時，Morgan Hill波作用下，CPD對模型橋的墩頂位移峰值減震率最大值達到了19.3%，且均超過了11%，而在Loma Prieta波和Northridge-01波作用下，其最大值為12.9%，最小值僅為4.1%；沿橫橋向激勵時，Morgan Hill波和Northridge-01波作用下，CPD對模型橋的墩頂位移峰值減震率最大值達到了30.4%，且均超過了10%，而在Loma Prieta波作用下，其最大值為9.0%，最小值僅為3.8%。

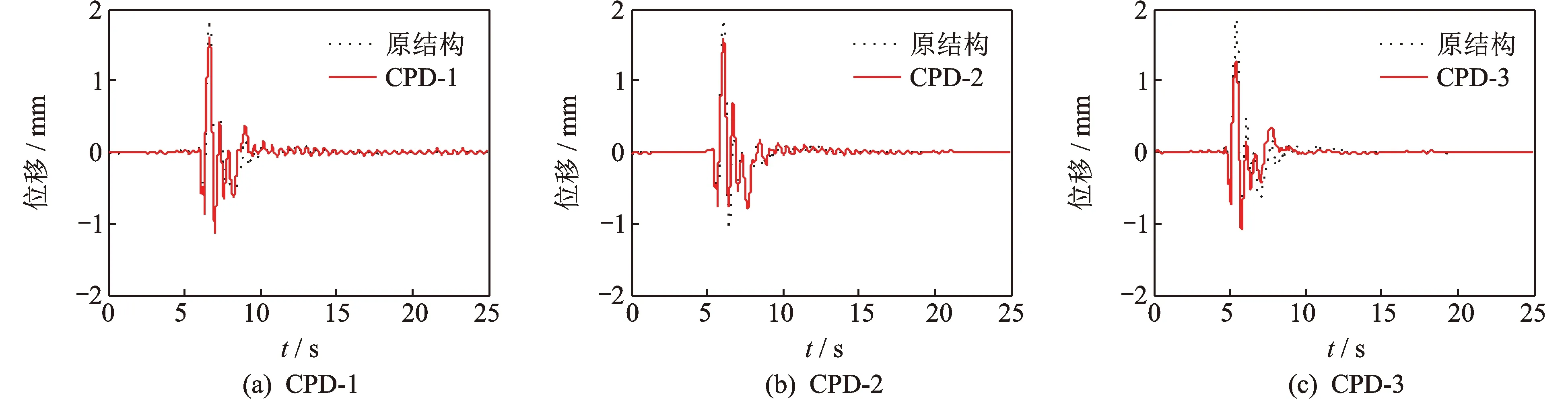
圖8 橫橋向E1作用下模型橋3#墩墩頂橫橋向位移響應曲線(Morgan Hill波)

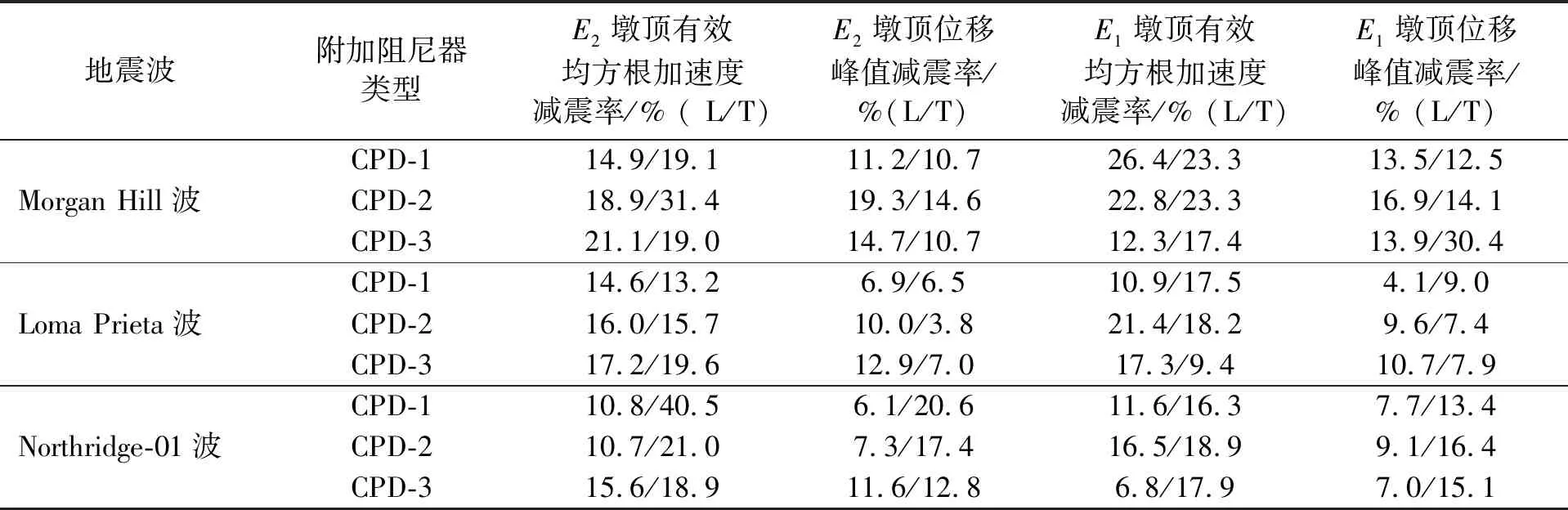
表7 近斷層地震作用下CPD減震控制效果