載流螺線環磁場的MATLAB仿真*

周鑫 李江珊 吳明和 滕保華

(電子科技大學英才學院 四川 成都 611731)(電子科技大學物理學院 四川 成都 610054)

1 引言

對于載流圓線圈和長直載流螺線管的磁場，無論是數學推導[1，2]、還是模擬仿真[3，4]，在教科書和文獻中已經有了詳盡的介紹和描述．然而關于載流螺線環磁場的分析卻比較少見[5]，既缺少對載流螺線環磁場的數學分析，也缺少對螺線環磁場的仿真計算．本文基于載流圓線圈的磁場，分別利用畢奧-薩伐爾定律和磁矢勢計算了不同密繞程度下載流螺線環的磁場分布，并利用MATLAB對載流螺線環的磁場進行了數值仿真，揭示了磁場隨距離、方位角度以及密繞程度的變化特征．

2 計算方法

下面分別從畢奧-薩伐爾定律[6，7]和磁矢勢[8]出發，計算不同密繞程度的載流螺線環的磁場．在計算時，螺線環中的每匝線圈用載流圓線圈代替，即螺線環的匝數就是圓環的個數，并且不考慮載流導線的直徑．

2.1 基于畢奧-薩伐爾定律的計算

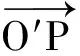
圖1 載流螺線環磁場示意圖

在圖1中，O′為螺線環上任取的一個載流圓線圈的圓心，φ為任一電流線圈平面上線圈圓心到電流元的矢量r1與電流線圈平面極坐標的極軸的夾角，容易得到圓線圈上任一電流元到P點的位置矢量為

r3=x-R1cosα-r1sinφcosαex+

y-R1sinα-r1sinφsinαey+

(z-r1cosφ)ez

而圓環上的電流元為

Ir1dφeτ

其中eτ表示在圓電流線圈的切向方向上的單位向量，則載流圓線圈在P點的磁感應強度為

(1)

從而載流螺線環在任一點P(x,y,z)的磁場強度為

(2.1)

(2.2)

(2.3)

2.2 基于磁矢勢的載流螺線環磁場的計算

參考平面上方位角α處的載流圓線圈在P點的磁矢勢可以表示為[8]

Ar2,θ,φ,α=Ar2,θ,φeφ=

(3)

進而由B=×A可以得到P點磁感應強度

Bα=Br2αer2+Bθαeθ+Bφαeφ

(4)

其中

eφ=er2×eθ

注意B(α)是α的函數，P點總磁感應強度B等于所有不同α處的圓電流對P點貢獻的磁感應強度B(α)累加，即

(5)

其中

(6.1)

(6.2)

(6.3)

比較以上兩種不同對螺線環磁場的計算方法可以發現，不管是基于畢奧-薩伐爾定律還是基于磁勢矢的計算方法，均物理概念明確，數學計算規范，而且便于仿真．

3 仿真分析與討論

以螺線環半徑r1=10 m，載流圓線圈半徑R1=3 m,電流I=1 A的螺線環為例，仿真不同密繞程度下載流螺線環的磁場分布．

3.1 磁場分布的整體特征

在匝數N=50，100，200等3種密繞程度下，利用MATLAB仿真了其磁場的整體分布．可以看出，當N較小時，毛刺現象嚴重；隨著密繞程度增加，螺線環的磁場變化越來越平滑．當N=200時，螺線環的磁場分布可近似為理想螺線環的分布，即磁場呈圓對稱分布，只有螺線環內部存在磁場．

圖2 3種情況下載流螺線環的磁場分布

3.2 磁場與距離的躍變特征

在螺線環參考平面上且方位角為零，計算了距離圓心任意距離處的磁場，圖3為MATLAB仿真的結果．

圖3 3種情況下載流螺線環的磁場躍變特征

可以看出，磁場分布呈現躍變性的特點，即在螺線環范圍之外的區域磁場幾乎為零，而在螺線環內磁場與離圓心的距離成反比關系．但當密繞程度低時，躍變不明顯，邊緣處緩慢上升或下降；當密繞程度高時，邊緣處陡升或陡降的躍變特征明顯．

3.3 磁場與角度的周期特征

在螺線環參考平面且在螺線環內半徑為9 m一個圓周上，計算了各點的磁場大小，其MATLAB仿真的結果如圖4所示，其中顯示出磁場分布隨角度變化的周期性．

圖4 磁場隨角度的變化關系

3.4 磁場與密繞程度的振蕩特征

在螺線環參考平面上，且在螺線環內半徑為12.5 m，方位角為零的一個固定位置，計算了密繞程度從N=0～150不同情況下，該固定點磁場的MATLAB仿真結果如圖5所示．從圖5可明顯看出，隨著密繞程度上升，該點的磁場大小呈總體上升的振蕩特征．

圖5 磁場隨密繞程度的變化關系

實際上，整體的上升性是由于隨著螺線環密繞程度的提高，螺線環的漏磁現象減弱，從而使得螺線環內部的磁場變大；而振蕩性則是由于隨著螺線環密繞程度的變化，該固定點與各個載流圓環的相對位置發生了往復變化，導致磁場疊加的結果是振蕩的．

4 結論

本文分別從畢奧-薩伐爾定律和磁矢勢出發，計算不同密繞程度的載流螺線環的磁場，并利用MATLAB仿真，得到了載流螺線環的磁場分布，從而對不同密繞程度情況下磁場分布呈現的躍變性、周期性、以及振蕩性等特點加深了認識．