圓環上涉及重值及虧量的亞純函數的唯一性
2019-12-26 09:51:36譚洋
純粹數學與應用數學 2019年4期
關鍵詞:理論
譚洋
(北京師范大學珠海分校應用數學學院,廣東 珠海 519085)
1 引言
假設讀者熟悉亞純函數的Nevanlinna值分布理論[1-2].亞純函數的唯一性問題是值分布論中的一個重要研究課題,平面上亞純函數的唯一性問題已經取得了豐碩的研究成果[3-5].文獻[6-7]將亞純函數的值分布理論推廣到多連通區域――圓環.之后有學者研究了圓環上的亞純函數唯一性問題[8].本文主要研究了圓環上重值及虧量對亞純函數及其導數唯一性的影響,所得結果豐富了圓環上亞純函數的唯一性理論.
本文采用圓環上亞純函數Nevanlinna理論的符號[6-7].設f(z)與g(z)為兩個非常數亞純函數,k為正整數,a為任意復數,如果f(z)?a與g(z)?a在計重數(不計重數)之下具有相同的零點,則稱a為f(z)與g(z)的CM(IM)公共值.Ek(a,f)表示f(z)?a的所有k重零點的集合(計算重數).Ek)(a,f)表示f(z)?a的≤k重零點的集合(計算重數);E(k(a,f)表示f(z)?a的>k重零點的集合.Ek(a,f)=Ek(a,g)表示f(z)?a的k重零點當且僅當是g(z)?a的k重零點.
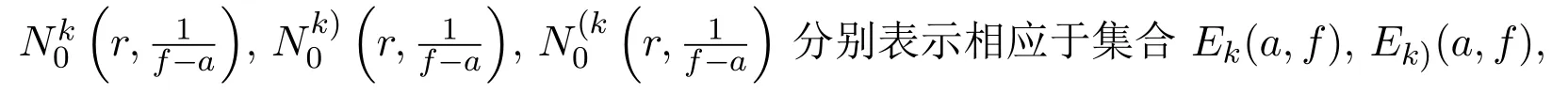

2 幾個引理





3 主要定理及證明
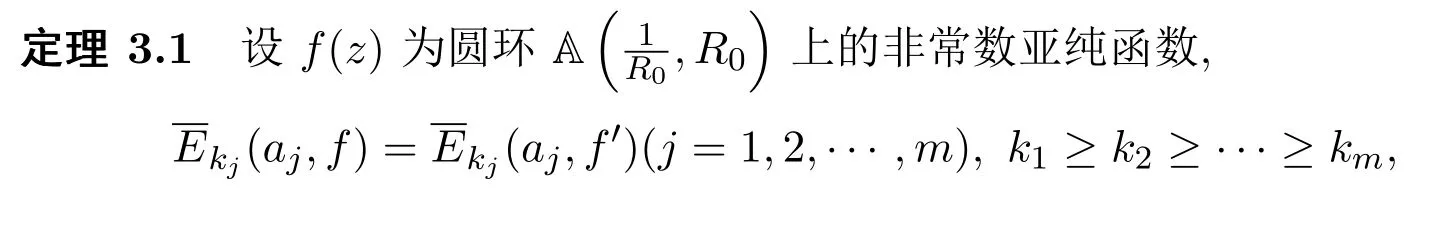







猜你喜歡
當代陜西(2022年5期)2022-04-19 12:10:18
新世紀智能(數學備考)(2021年9期)2021-11-24 01:14:28
湘潮(上半月)(2021年4期)2021-07-20 08:05:28
汕頭大學學報(自然科學版)(2020年4期)2020-12-14 07:05:00
讀與寫·教育教學版(2017年10期)2017-11-10 22:28:57
大電機技術(2017年3期)2017-06-05 09:36:02
廣州大學學報(社會科學版)(2016年1期)2016-06-24 09:46:02
區域經濟評論(2016年2期)2016-05-17 05:06:43
學習月刊(2015年21期)2015-07-11 01:51:44
社會生活探索(2013年0期)2013-10-24 03:44:40

