帶單參數q的無限維Block型李代數的性質

余德民,方春華

(湖南理工學院數學學院,湖南 岳陽 414006)

1 引言

Virasoro-like李代數是在20世紀80年代作為擬多項式環的一階微分算子代數被引入的,90年代在理論物理的廣義對稱性研究中產生了同樣的代數結構.設C為復數域,Z為整數加群,文獻[1]定義了一類Virasoro-like李代數,并研究了Virasoro-like李代數的單性,設是由L(a1,a2)(?a1,a2∈Z),張成的復數域C上的線性空間,李運算定義如下:

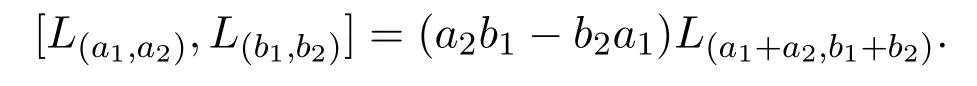
此運算在基向量上線性擴張,并滿足反對稱性和Jacobi不等式,稱為Virasoro-like李代數.文獻[2]研究了Virasoro-like的導子代數和導子代數的自同構群,文獻[3]研究了帶參數的α,β的Virasoro-like的導子代數,文獻[4]研究了廣義Virasoro李代數.文獻[5-9]研究了Virasoro李代數及其推廣的Virasoro李代數.本文研究一類單參數q的無限維Block型李代數g,這類李代數是Virasoro-like李代數的推廣,g為C上線性空間,其基向量為L(a1,a2)(?a1,a2∈Z),張成的復數域C上的線性空間,李運算定義如下:

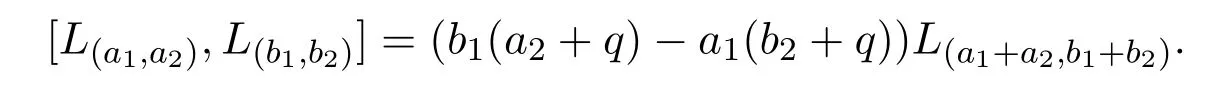
此運算在基向量上線性擴張,其中q為復數,并滿足反對稱性和Jacobi不等式,稱g為參數q的無限維Block型李代數,當參數q=0,帶參數q的無限維Block型李代數g便是Virasoro-like李代數.文獻[10-12]研究了一類帶單參數q的無限維Block型李代數的結構分類,導子和自同構和最高權模.

本文研究了這類李代數的子代數,同構和同態.

2 主要結果