閘門調度對下游河岸沖刷影響規律的研究方法探討

肖小玲，沈家文

(1. 福建華電金湖電力有限公司，福建 將樂 353300；2. 武漢大學水利水電學院，湖北 武漢 430072)

水力調控是工程上實現電站下游防治沖刷的有效手段，一般采用閘門調度的方式來完成[1]。此前已有很多學者對電站下游沖刷進行了研究，如下游沖刷引起的河床演變趨勢以及河勢的走向等問題。其主要的研究內容是分析河道水流結構形態對邊坡穩定的影響規律[2-3]。為了得到科學精準的閘門調度方案，可通過原型資料分析[4]、物理模型觀測[5]和數學模型計算[6]等三種方法進行研究。但是原型資料的收集難度較大，且資料范圍具有局限性，不能完全依托資料高效快速地分析得到閘門調度方案；而物理模型和數學模型都是由于其模擬的復雜性導致不能靈活地進行閘門調度試驗。通過調查發現，人工神經網絡模型在閘門調度的水文方面已經開展了研究[7]，但討論閘門調度對下游河岸沖刷影響的研究還不是很多。

因此，本文基于物理模型試驗，觀測不同洪水頻率工況時不同閘門調度方案下電站下游河道水流動力條件與邊坡沖刷影響的對應關系，討論如何通過神經網絡高效快速地分析研究閘門調度中影響下泄流量的各因素對下游河道內水流動力條件改變程度的敏感性，進而得到閘門調度對邊坡沖刷的影響規律，這對高唐電站閘門調度運行管理具有科學的指導意義。

1 研究區域與資料

高唐水電站位于福建省西北部的將樂縣高唐鎮上游約2.5 km處，為閩江上游金溪流域梯級開發的第七級電站。水電站采用河床徑流式，以發電為主。壩址以上流域面積6 683 km2，流域內雨量充沛，多年平均降雨量1 684 mm，多年平均來水量68.43億m3，多年平均流量217 m3/s，水庫正常高水位146.00 m，對應庫容2 144萬m3，是一個日調節水庫。泄水閘壩段布置在主河床的中部，泄水閘壩長172 m，閘壩高程153 m，共9孔，溢流堰頂高程134 m，孔口尺寸：15 m×12 m(寬×高)，駝峰式溢流堰，采用弧形鋼閘門擋水。閘后采用底流和戽流相結合的消能方式，中間4孔閘(4～7號孔)采用底流消能，閘后設37 m長的消力池，兩端剩余的5孔閘為戽流消能，在閘后設鋼筋混凝土短護坦，長15 m。電站樞紐平面布置見圖1。

圖1 高唐水庫電站樞紐平面布置示意圖

由于大壩左岸下游河岸建設期未設置防護工程，2007年投產以來，每年洪水季節，當大壩下泄洪水重現期超過五年一遇時，左岸岸坡均有不同程度的沖刷，岸坡坡腳不斷后退。為了減小高唐水電站下游左岸邊坡崩岸所產生的負面影響，需要通過簡易方便的數學模型來分析庫區來流、閘門調度方式與電站下游河岸水動力條件之間的對應關系，研究合理的水電站閘門開啟方式和調度方案，調控電站閘門下泄水流流態，實現下泄水流消能效果最佳，以期改變電站下游左岸沖刷河段內水流結構。

2 研究方法

2.1 數學模型方法

高唐水電站泄洪閘孔數較多，理論上閘門開啟組合形式復雜，物理模型試驗難以全部模擬閘門調度組合。因此需要建立一個可以實現閘門調度對下游河道水力條件變化控制影響的耦合數學模型。本文擬準備選擇通過改變下游水力條件(流量、水流結構和流速等)，動態調整一般水動力模型中縱向和橫向分速度的數值。采用試驗監測與多方法估算相結合的手段，增加模型參數的確定性以及對不同水力條件的自適應能力。

2.1.1 閘門調度與流量的響應模型

為了比較具體化地定量研究閘門調度對水量的調配和電站下泄水流流量的影響，本文擬采用3層BP(back-propagation)神經網絡模型[8]對閘門調度與電站下泄流量之間進行多元關系擬合。其擬合計算結構示意圖如圖2所示。

圖2 人工神經網絡擬合計算結構示意圖

由圖2可知，在擬合計算結構中輸入層共4個神經元，分別為庫區壩前水位、開閘孔數、閘門開度和開閘排列，而輸出層為閘門下泄流量。本文中人工神經網絡模型中樣本的劃分及訓練方法采用提前終止法[9]，其訓練樣本為高唐水電站物理模型試驗觀測的資料結果，其可靠性良好。對神經網絡模型結果處理采用歸一化三維空間內的曲面觀測分析方法，通過觀測曲面上壩前水位、開閘孔數、閘門開度和開閘排列等4個變量對閘門下游下泄流量之間的相應關系，可以得到各影響因素與下泄流量的相關性明顯程度，進一步得到閘門頻繁調度工況下調控下泄流量的變化特性。

2.1.2 流量與河岸沖刷速度的響應模型

在不考慮電站閘門調度以及消力池消能防沖的影響后，從不影響末端開始可以認為橫斷面為自然河道斷面。雖然河道水力半徑會隨著下泄流量不同而變化，但通過水文觀測，在同一河道斷面中其平均流速大小與下泄流量一般會呈對應關系。在本文通過物理模型試驗觀測壩后50 m的同一斷面，其觀測斷面和觀測點如圖3所示。

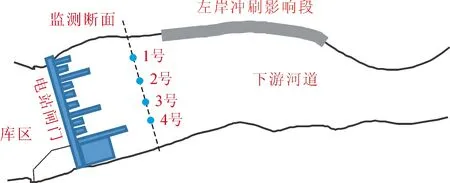
圖3 物理模型試驗中流速觀測斷面及觀測點位布置圖

監測斷面上布置4個流速監測點，采用ADV測量各監測點的三維流速。不同的壩前水位、開閘孔數、閘門開度和開閘排列會導致監測點位上流速發生變化。根據水力學及河流動力學知識，可認為壩下游左岸沖刷速度主要受到水力直接沖擊的直接影響，而沖刷速度矢量主要由速度矢量在垂直于左岸方向的速度分量和速度矢量向左岸的偏移角度共同決定。各監測點位流速作用示意圖如圖4所示。

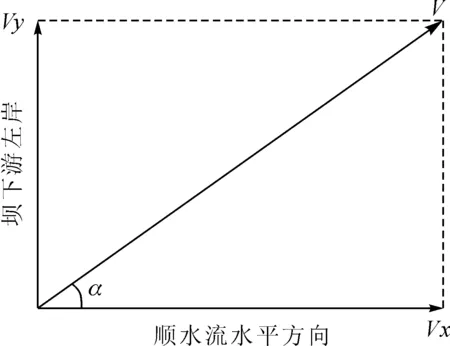
圖4 壩下游左岸沖刷速度作用示意圖

定義壩下游左岸沖刷速度的貢獻U為

(1)

式中：Vxi和Vyi分別代表第i個監測點位上水平面中順水流水平方向的速度分量大小、指向壩下游左岸方向的速度分量大小；N為監測點位的個數。

在具有其獨立的自然屬性的河道上，不同的壩前水位、開閘孔數、閘門開度和開閘排列所決定的下泄流量，必將與下游沖刷速度V是一一對應關系。因此，就可以建立流量與河岸沖刷速度的貢獻響應數學模型。

2.2 模型敏感性分析方法

現階段在諸多數學分析領域都采用敏感性分析方法來研究和預測數學模型中具有屬性的輸入層在可能取值范圍內變動對輸出層數值的影響程度。通過研究數學模型屬性的敏感性系數的大小來分析輸入變量對輸出變量的重要性。其內容核心為考慮合理存在的屬性敏感性系數，計算并對各屬性敏感性系數排序，通過排序結果分析各屬性的重要程度。而敏感性分析又分為局部敏感性分析和全局敏感性分析。其中全局敏感性分析可以分析數學模型中所有屬性對模型輸出的影響，以及各屬性之間的彼此作用對模型輸出的影響。

因此，建立閘門調度與下游沖刷的響應神經網絡數學模型后，評價電站閘門調度對下游沖刷的影響，可進一步對該模型的參數進行全局敏感性分析。目前常見的全局敏感性分析方法，主要分為PAD2法[10]、EFAST法、Sobol法[11]以及基于ANN的權值分析法[12]等。

2.2.1 敏感性分析方法的選擇

通過統計現階段對數學模型全局敏感性分析方法，可以分析得到各種方法的優劣。將四種全局敏感性分析方法進行對比，可得到表1所示的統計成果。

由表1可知，對于數學模型的全局敏感性分析方法最優選擇Sobol法，這也是目前最常用的使用方法，已經被廣泛地運用于經濟、醫藥、生物、環境以及社會學等各大領域的數學模型分析中。但是由于該方法計算量較大，所以針對其不足已經有人研究出了Sobol法的改進算法，以此來解決該方法的不足。因此，在本文中建議采用Sobol法的改進算法來分析閘門調度對下游沖刷速度的響應模型的敏感性分析。

但又由于神經網絡模型屬于黑箱模型，其響應曲面的結構難以確定。模型的敏感性分析結果對分析過程采樣量的依賴性很高，所以僅采用Sobol法的改進算法來分析模型的全局敏感性是不夠的。因此在本文中需要進一步采用計算方法簡單的ANN權值分析法來驗證全局敏感性分析結果的可靠性。即在全局敏感性分析的基礎上，通過了ANN權值分析法驗證的結果才是科學可靠的敏感性成果。而且其計算過程簡單，應用十分廣泛，所以在本文中建議運用。

表1 全局敏感性分析方法的對比結果表

2.2.2 敏感性分析的內容

考慮到人工神經網絡在數學模型計算中復雜性，首選考察該模型在閘門調度對下游流量方面的敏感性，可通過ANN的權值分析法計算壩前水位、開閘孔數、閘門開度和開閘排列等4個屬性變量的相對重要性指數I，將其作為Sobol方法對模型全局敏感性分析成果的驗證對象。當4個屬性變量的相對重要性指數I在兩種方法中的結果一致時，那么全局敏感性分析成果可采納；而當結果不一致時，那么全局敏感性分析過程中的訓練樣本需要進一步增加。

再采用Sobol方法對模型各因子對壩下游左岸沖刷速度的影響進行評估。評估過程應該保證采樣數量，在計算時間精簡的前提下只有采樣數量足夠多，根據中心極限定理——蒙特卡羅法計算得到的敏感性指數才真實。即在實際數學試驗模型分析中，在保證足夠的樣本數量的前提下，根據各因子分布特征選擇合適的樣本數對應的敏感性指數成果，該成果在基本穩定狀態下才被認為有效。

閘門調度對下游左岸沖刷數學模型的全局敏感性分析的內容表達形式主要包括總敏感性指數和各因子的一階敏感性指數。其中總敏感性指數是表示數學模型中各因子彼此之間共同作用對下游左岸沖刷過程產生的影響程度，而一階敏感性指數則是表示單一因子獨立對下游左岸沖刷過程的影響程度。敏感性分析結果一般各因子會按照一階敏感性指數的大小進行大小排序。而根據各因子的敏感性大小，可以進一步分析得到各因子對閘門下游左岸沖刷過程的貢獻度，也為分析閘門調度對下游沖刷影響規律提供了科學依據。

3 結 語

本文建議采用人工神經網絡建立閘門-流量模型，并結合流量與下游左岸沖刷速度的響應關系，估算高唐電站閘門調度方式對下游左岸沖刷的影響，可評價模型中各參數對下游左岸沖刷過程的敏感度，得到以下結論：

1)基于閘門水流流動過程的物理過程，簡化下泄流量與左岸沖刷的對應關系，通過神經網絡可以將閘門調度中各種影響因素-下泄流量-下游左岸沖刷速度建立成為一種響應的數學模型；

2)采用Sobol方法與權值分析法一起分析模型的敏感性，既能保證閘門調度對下游左岸沖刷影響模型的敏感性結果可靠，也能通過Sobol方法計算得到各影響因子之間的敏感性相對大小順序，進而得到各影響因子對壩下游左岸沖刷的作用規律。