纜松弛補(bǔ)償器液壓管路邊界層厚度與溫度耦合關(guān)系仿真分析

(大連海事大學(xué) 輪機(jī)工程學(xué)院，遼寧 大連 116026)

在對(duì)液壓系統(tǒng)故障的研究中，大多主要集中在故障診斷、故障定位及故障原因查找等方面，而對(duì)當(dāng)前液壓系統(tǒng)狀態(tài)正常但存在故障隱患的預(yù)測(cè)研究較少[1]。對(duì)液壓系統(tǒng)特征參數(shù)的提取主要利用單一的時(shí)域、頻域和時(shí)頻聯(lián)合域指標(biāo)構(gòu)建特征向量，不能有效地反映故障信息[2]。且現(xiàn)有對(duì)液壓系統(tǒng)運(yùn)行狀態(tài)的研究從宏觀入手較多，大多通過利用硬件、軟件對(duì)液壓系統(tǒng)運(yùn)行過程中的動(dòng)態(tài)參數(shù)進(jìn)行采集、處理，建立特征參量與故障類型的映射模型[3-7],或以傳感器為基礎(chǔ)研制檢測(cè)儀[8-9]。研究工作主要是針對(duì)整機(jī)設(shè)備對(duì)液壓設(shè)備狀態(tài)進(jìn)行評(píng)估，而對(duì)特定部件微觀的狀態(tài)評(píng)估研究較少。液壓系統(tǒng)管路的宏觀狀態(tài)特性與微觀的狀態(tài)特性息息相關(guān)，可反映液壓系統(tǒng)的實(shí)時(shí)狀態(tài)[10]。因此，如果從邊界層理論出發(fā)，并且將現(xiàn)有的MEMS傳感器技術(shù)引入到船舶液壓系統(tǒng)中，研究邊界層與液壓系統(tǒng)參數(shù)的關(guān)系，可實(shí)現(xiàn)大系統(tǒng)復(fù)雜信息感知領(lǐng)域的理論突破。

在眾多需要監(jiān)測(cè)并分析的液壓系統(tǒng)特征狀態(tài)參數(shù)中，溫度的變化將顯著影響液壓系統(tǒng)的整體性能，而液壓系統(tǒng)邊界層狀態(tài)在溫度變化中起主導(dǎo)作用。因此，考慮基于傳統(tǒng)船舶液壓故障預(yù)測(cè)與診斷的理論，分析液壓管路邊界層與溫度的耦合，為液壓系統(tǒng)的故障預(yù)測(cè)和監(jiān)測(cè)新手段提供理論支撐。

1 流動(dòng)方案設(shè)計(jì)

所選管路在工作時(shí)，其允許的運(yùn)動(dòng)黏度范圍為10～380 mm2/s。在FLUENT管路流動(dòng)仿真中，對(duì)于不同的流動(dòng)狀態(tài)，應(yīng)采用不同的管道內(nèi)流動(dòng)的模型。通過式(1)來計(jì)算該管道內(nèi)流動(dòng)情況的雷諾數(shù)，根據(jù)雷諾數(shù)來設(shè)置相應(yīng)的流動(dòng)模型。

Re=ρVd/μ

(1)

式中：V，ρ，μ分別為流體的流速、密度與黏性系數(shù)；d為特征長(zhǎng)度,即管的直徑。

管路流動(dòng)研究采取控制變量法，對(duì)科考船絞車系統(tǒng)纜松弛補(bǔ)償器液壓系統(tǒng)正常管路中的邊界層特性分析的具體方案見表1。

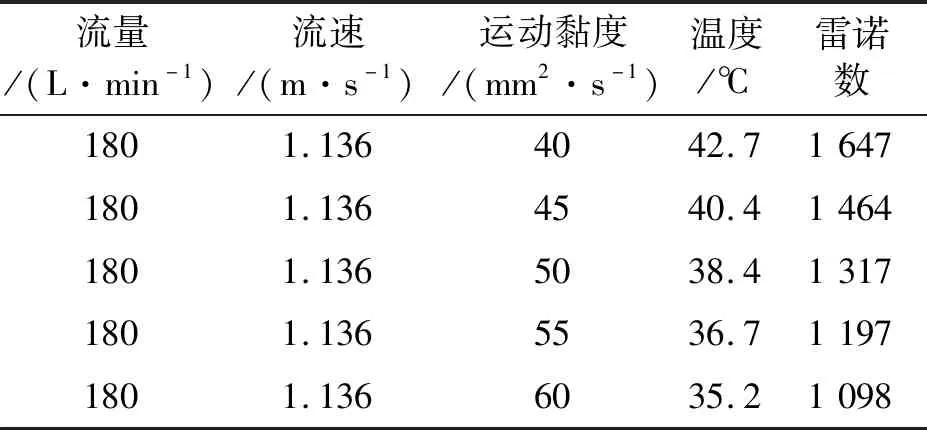
表1 層流情況下，不同運(yùn)動(dòng)黏度的管路流動(dòng)方案

由管路參數(shù)、液壓油參數(shù)和流動(dòng)情況，根據(jù)式(1)求得各黏度對(duì)應(yīng)的雷諾數(shù)和湍流-層流轉(zhuǎn)變運(yùn)動(dòng)黏度為28.65 mm2/s。

2 FLUENT模型建立

利用FLUENT軟件層流穩(wěn)態(tài)模型對(duì)三維密封管道進(jìn)行數(shù)值模擬。模擬遵循流體力學(xué)三大方程，即質(zhì)量守恒方程 、動(dòng)量守恒方程和能量守恒方程[11]。

為了符合實(shí)際工況，模型充分考慮了現(xiàn)實(shí)中纜松弛補(bǔ)償器液壓系統(tǒng)液壓泵出口管路的布置，模型的管路直徑采用58 mm，其尺寸是纜松弛補(bǔ)償器液壓系統(tǒng)液壓泵出口管路的直徑大小。運(yùn)用三維建模軟件SOLIDWORKS建立纜松弛補(bǔ)償器液壓系統(tǒng)液壓泵出口管路的三維模型，見圖1。

圖1 液壓泵出口管路三維模型

選取纜松弛補(bǔ)償器液壓系統(tǒng)部分液壓管路，基于FLUENT中管路穩(wěn)態(tài)流動(dòng)分析，采用控制變量法，對(duì)正常纜松弛補(bǔ)償器液壓系統(tǒng)管路中的邊界層特性進(jìn)行分析，為后面研究提供參考值。該纜松弛補(bǔ)償器液壓系統(tǒng)液壓站的主要參數(shù)以及L-HM46 礦物油型液壓油參數(shù)分別見表2、3。

表2 纜松弛補(bǔ)償器液壓系統(tǒng)液壓站參數(shù)

表3 L-HM46 礦物油型液壓油參數(shù)

采用基于壓力的穩(wěn)態(tài)隱式求解器，根據(jù)設(shè)計(jì)方案，模型的雷諾數(shù)范圍是1 098.2～1 647.2，所以選取層流流動(dòng)模型。流場(chǎng)操作壓力為工作壓力。

根據(jù)模擬流場(chǎng)設(shè)置邊界條件：假設(shè)液壓油在管道內(nèi)部不可壓縮流動(dòng)，采用速度入口邊界條件，入口速度為1.136 m/s，方向?yàn)榇怪边M(jìn)口，液壓管的入口為完全均勻流動(dòng)。出口條件采用outflow出口邊界條件。壁面邊界條件設(shè)置為絕熱壁面。由于在液壓系統(tǒng)中，液壓油的黏度會(huì)隨著溫度的改變而改變，所以在材料屬性設(shè)置中，不能簡(jiǎn)單的設(shè)置為常數(shù)。根據(jù)液壓工程師技術(shù)手冊(cè)[12]中，液壓系統(tǒng)常用的礦物型液壓油，當(dāng)40 ℃時(shí)運(yùn)動(dòng)黏度小于135 mm2/s，且溫度在30～150 ℃范圍內(nèi)，用經(jīng)驗(yàn)公式計(jì)算得到不同溫度時(shí)液壓油的運(yùn)動(dòng)黏度。

(2)

式中：ν40為溫度為40 ℃時(shí)液壓油的運(yùn)動(dòng)黏度；n為指數(shù)，隨液壓油運(yùn)動(dòng)黏度變化，見圖2。

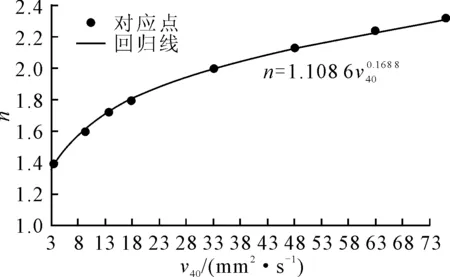
圖2 40 ℃時(shí)，液壓油運(yùn)動(dòng)黏度與指數(shù)對(duì)應(yīng)關(guān)系

由此得到液壓油運(yùn)動(dòng)黏度與指數(shù)關(guān)系式。

(3)

通過式(3)得到所用液壓油對(duì)應(yīng)的指數(shù)為2.115 6。一般液壓油最低工作黏度為14 mm2/s。根據(jù)式(3)描繪纜松弛補(bǔ)償器液壓系統(tǒng)選用液壓油的黏溫圖，見圖3。

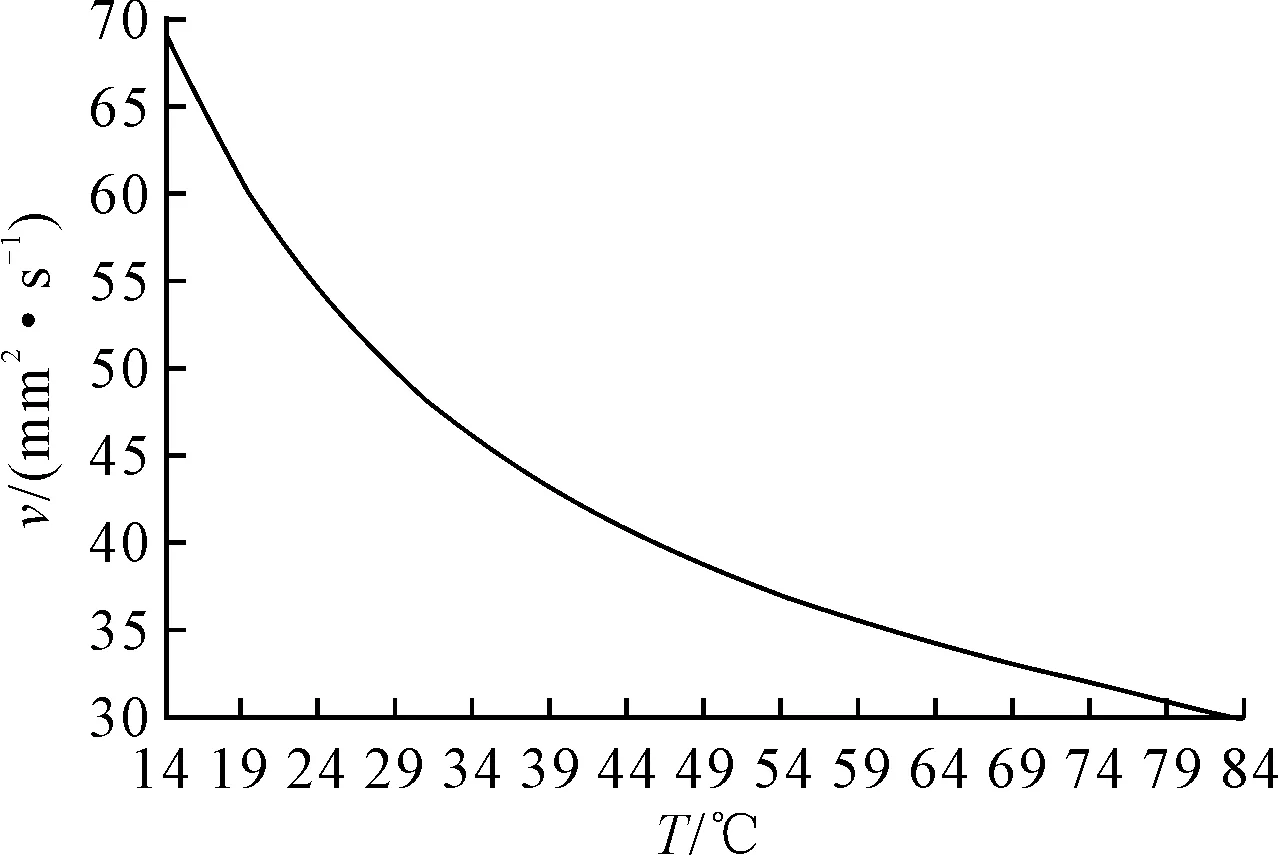
圖3 液壓油運(yùn)動(dòng)黏度-溫度

根據(jù)纜松弛補(bǔ)償器液壓系統(tǒng)選用液壓油的黏溫關(guān)系式，編寫自定義函數(shù)(user define function，UDF)來實(shí)現(xiàn)液壓油運(yùn)動(dòng)黏度隨溫度變化函數(shù)。

3 仿真結(jié)果分析

通過FLUENT模擬仿真計(jì)算，得到進(jìn)口體積流量qV,in=2.999 364 7×10-3m3/s。出口體積流量qV,out=-2.999 372 4×10-3m3/s，以及進(jìn)出口的體積流量差ΔqV=-7.688 631 2×10-9m3/s。相對(duì)流量差|ΔqV/qV,in|=2.563 4×10-6，當(dāng)|ΔqV/qV,in|≤0.5%時(shí)認(rèn)為質(zhì)量守恒。

管道0.35 m處的截面情況見圖4，從管道截面中心點(diǎn)沿徑向方向(y方向)到管壁的流速，該區(qū)域是屬于邊界層發(fā)展階段。

圖4 從截面中心點(diǎn)沿徑向方向的流速

圖4顯示出管道在該方向分布的流速，在管壁內(nèi)流速為0，然后向著中心點(diǎn)逐漸增加，曲線形狀呈拋物線狀。由于該處是處于邊界層發(fā)展階段，所以邊界層厚度小于半徑，但隨著管道流動(dòng)，邊界層厚度會(huì)逐漸增加。

管道出口截面流速分布見圖5。對(duì)應(yīng)的流動(dòng)情況見圖6。

圖5 出口截面流速云圖

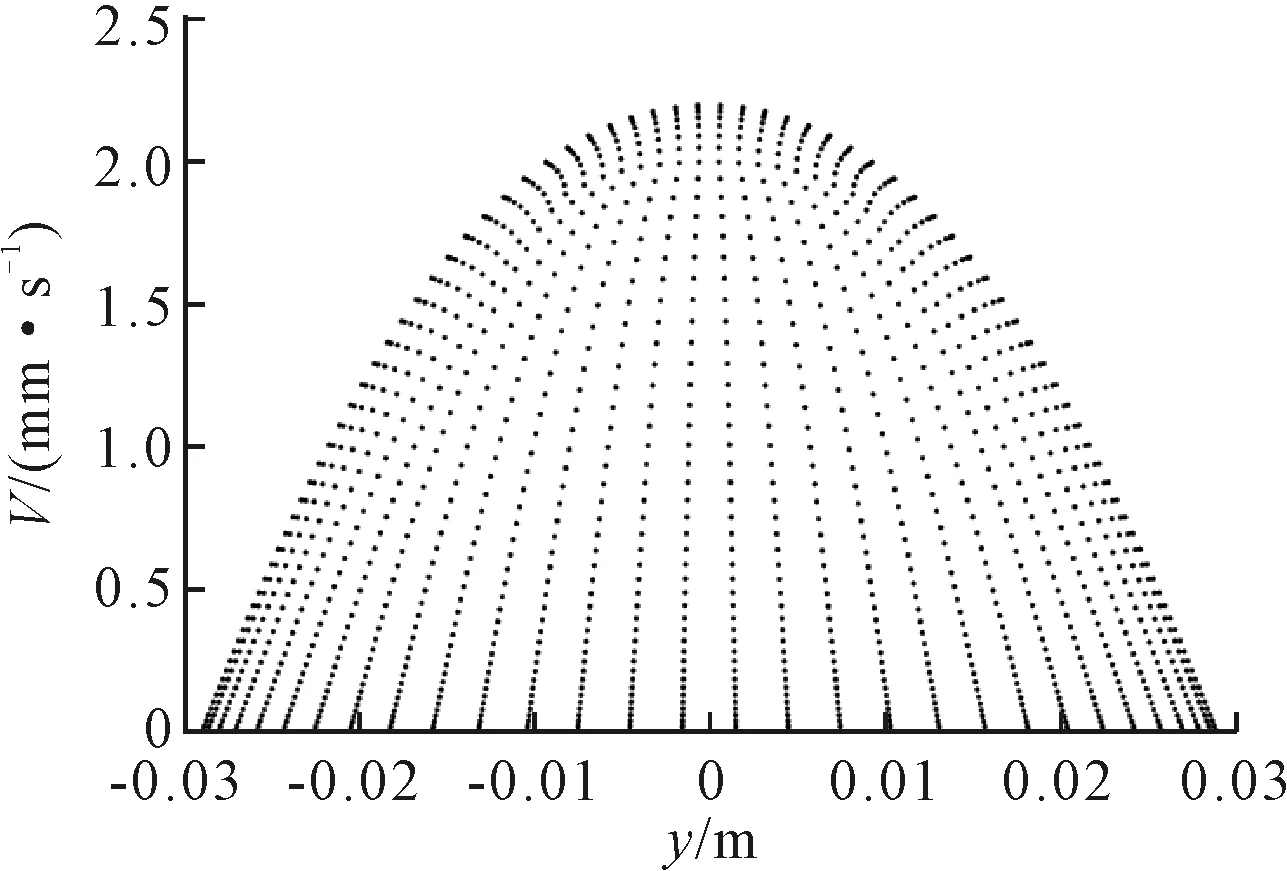
圖6 出口截面流速的變化情況

通過圖5和圖6可以看到，管道出口截面流速數(shù)值大小呈拋物線狀，截面中心流速最大，然后沿徑向方向逐漸減少，直到管壁處流速為0。由于出口處邊界層已經(jīng)發(fā)展完畢，流速最大在截面中心處，其符合圓直管流動(dòng)的現(xiàn)實(shí)情況。通過該方案進(jìn)行模擬管道流動(dòng)，滿足圓直管層流流動(dòng)規(guī)律[13]。因此，可以通過該方案分析液壓系統(tǒng)的液壓管道在各種情況下的管道邊界層流動(dòng)情況。

3.1 邊界層厚度

邊界層的厚度是從物面(即當(dāng)?shù)厮俣葹榱愕牡胤?開始，沿法線方向速度與當(dāng)?shù)刈杂闪魉俣萓相等的位置之間的距離。邊界層由繞流物體頭部起，邊界層厚度是從零開始沿流動(dòng)方向開始逐漸增大，見圖7。

圖7 邊界層厚度示意

圖7中x表示流體沿管道壁面流動(dòng)方向，y表示壁面到管道軸心的距離。在離開壁面不遠(yuǎn)的地方，邊界層內(nèi)的速度就已接近于外部速度。為了方便對(duì)管道各截面的邊界層進(jìn)行研究和數(shù)據(jù)提取，定義邊界層厚度為截面最大速度的99%處到截面流動(dòng)速度為0處(即管壁處)，計(jì)算公式為

L(x)=l|uy=0.99U

(4)

式中：L(x)為管距為x截面處的邊界層厚度；l為速度為uy時(shí)的實(shí)時(shí)邊界層厚度；uy為管道的第x截面的徑向方向上，距管管道軸心距離為y處的流動(dòng)速度；U為為第x截面最大流動(dòng)速度。

3.2 邊界層厚度與系統(tǒng)溫度參數(shù)的耦合分析

38.4 ℃時(shí)管道前端的速度云圖見圖8、9。

圖8 38.4 ℃時(shí)管道前端速度云圖

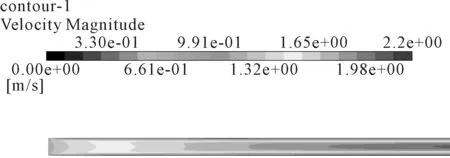
圖9 38.4 ℃時(shí)管道前端速度云圖局部

由于各溫度的管道前段速度云圖規(guī)律相似，因此選擇單個(gè)溫度的管道前端速度云圖作分析。可以看出，管道前端內(nèi)的邊界層速度都是在進(jìn)口均勻速度流進(jìn)后，隨著流體向前流動(dòng)。由于管壁的影響，來流速度在壁面處速度逐漸減少，并且在靠近管壁區(qū)間很薄的流體層中減少作用最嚴(yán)重，由此可見流動(dòng)的速度梯度大。

由于不考慮液壓油的壓縮性，所以在管道內(nèi)流體流動(dòng)一定的距離后，管道的總流量不變，中心流速慢慢增加。由于流速增加，管道內(nèi)的壓力隨著流動(dòng)方向遞減，見圖10。

圖10 管道內(nèi)截面軸線速度矢量圖

通過液壓管道流動(dòng)軸向速度的分布情況分析，獲得管道流動(dòng)邊界層厚度情況。對(duì)于在液壓管道內(nèi)流動(dòng)，在正常工況下，邊界層厚度是隨著流動(dòng)方向慢慢增加。從圖11中可以看到邊界層厚度的發(fā)展呈近線性增長(zhǎng)，并且在1 m后會(huì)增加減慢速度。從42.7 ℃，0.5 m內(nèi)邊界層厚度發(fā)展曲線為V=-0.02x2+0.030 5x+0.004 6，對(duì)于其他不同運(yùn)動(dòng)黏度，邊界層厚度發(fā)展情況與圖8近似。

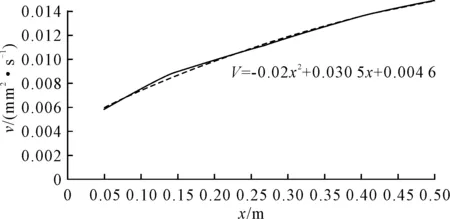
圖11 42.7 ℃，0.5 m內(nèi)邊界層厚度變化

設(shè)計(jì)方案中5種不同管道液壓油溫度情況下(42.7～35.2 ℃)，管道邊界層厚度與管軸線方向距離的關(guān)系見圖12。

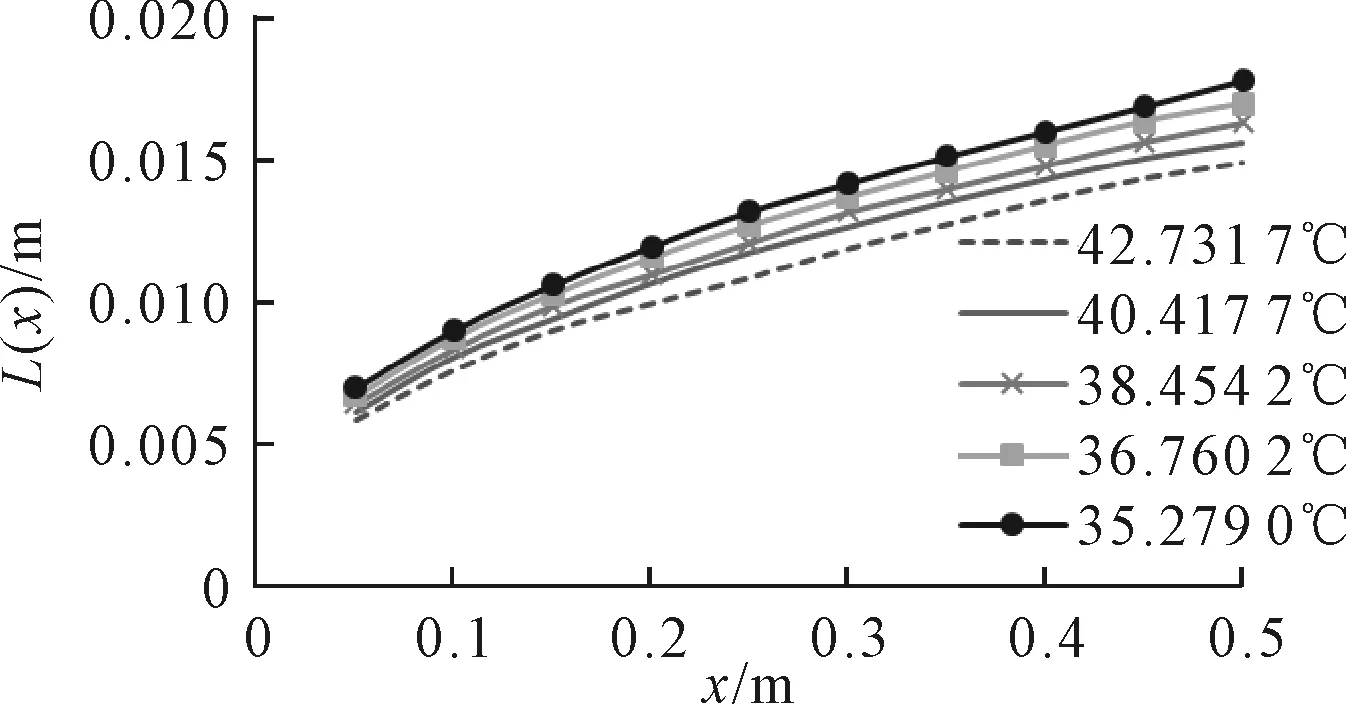
圖12 邊界層厚度沿管軸線方向發(fā)展的變化

由圖12可見，42.7 ℃溫度下，邊界層厚度增長(zhǎng)速度最快。36.7 ℃溫度下，邊界層厚度增長(zhǎng)速度最慢。圖中顯示邊界層厚度的增長(zhǎng)速度是隨著管道液壓油溫度而變化，即管道內(nèi)液壓油溫度的增大，邊界層厚度增長(zhǎng)速度也將會(huì)隨之增大。因此，認(rèn)為在液壓系統(tǒng)管道邊界層發(fā)展階段區(qū)域，同一管道位置上，液壓系統(tǒng)液壓油溫度與邊界層厚度呈反比關(guān)系。同時(shí)，在管道邊界層發(fā)展階段區(qū)域中，液壓系統(tǒng)液壓油溫度也與邊界層厚度增長(zhǎng)速度呈反比關(guān)系。

4 結(jié)論

通過仿真提取到液壓系統(tǒng)溫度與邊界層厚度的耦合數(shù)據(jù)，分析得到系統(tǒng)溫度與邊界層厚度的關(guān)系。下一步可在實(shí)驗(yàn)中通過MEMS傳感器提取邊界層相關(guān)參數(shù)進(jìn)行驗(yàn)證。此方法從邊界層的參數(shù)出發(fā)，通過液壓油管路邊界層與系統(tǒng)參數(shù)耦合，尋找微觀上的變化規(guī)律，實(shí)現(xiàn)對(duì)液壓系統(tǒng)的狀態(tài)的預(yù)測(cè)和提前診斷，從而提供一種實(shí)現(xiàn)對(duì)液壓系統(tǒng)故障預(yù)防及提前診斷的新方法。