基于自適應多特征匹配的移動機器人SLAM研究*

茹淑慧, 王紅旗, 唐 浩

(河南理工大學 電氣工程與自動化學院，河南 焦作 454000)

0 引 言

近年來，同時定位與地圖構建(simultaneous localization and mapping,SLAM)技術在機器人領域受到了廣泛的關注和應用，被研究者普遍認為是實現機器人完全自主的關鍵[1]。其中，最常用的掃描匹配技術是標準迭代最近點(iterative closest point,ICP)算法[2,3]。ICP算法通常使用相鄰兩幀掃描數據點集進行匹配[4]，但是由于掃描數據點數量較大，導致該算法計算負荷較大，收斂速度較慢。許多學者對ICP算法進行改進，大都從掃描數據中提取特征，利用特征匹配來求解相對位姿。文獻[5]采用從掃描數據中提取特征點進行ICP匹配，減少了匹配時間，提高了SLAM算法的快速性，但該方法適合于具有清晰的線段或角點特征的多邊形結構化環境。文獻[6]采用了一種基于幾何統計特征的全局掃描匹配方法，利用“試探—驗證—求解”(probing verification solution,PVS)的匹配策略獲得掃描之間的相對位姿。文獻[7,8]采用多特征關聯方法來提高匹配的精度，但該方法在匹配策略中分配固定的加權值，在復雜多變的環境中缺乏適應性。

本文采用激光掃描儀對環境進行掃描，獲取掃描數據點集。首先對掃描數據點集進行區域分割，提取區域的多特征信息；然后利用區域的多特征信息對ICP算法的匹配策略進行改進，得到與下一幀區域的相關性，并自適應調整多特征的加權系數從而保證ICP匹配的精度，最終實現了移動機器人的同步建圖與定位。

1 掃描匹配的問題描述

掃描匹配算法的地圖構建與定位是對相鄰兩個掃描數據點集進行匹配[9]，得到兩組點集之間的旋轉矩陣和平移向量(R,T)。掃描匹配算法的示意圖，如圖1所示。

圖1 掃描匹配算法示意

設Pk-1={Pi,k-1(xi,k-1,yi,k-1)|i=1,2,…,n}為k-1時刻的掃描數據點集,Qk={Qj,k(xj,k·yj,k)|j=1,2,…,m}為k時刻的掃描數據點集。

匹配前，先將k時刻的掃描數據點集轉換到k-1時刻的坐標下，令Q′j,k=RQj,k+T，然后以式(1)中E(R,T)達到最小值為評價標準，求解位姿變換參數R,T

(1)

式中R(Δθ)為兩組點集的旋轉矩陣，Δθ為旋轉角度，T=[Δx,Δy]′為兩組點集的位移向量，Pi,k-1和Qj,k為兩組點集中的對應點，N為對應點的數目。

2 基于自適應多特征掃描匹配的SLAM方法

2.1 自適應變閾值分割方法

原始掃描數據量較大，而且還存在噪聲點，直接進行掃描匹配會影響定位與地圖構建的實時性，因此，應先對掃描數據進行區域分割。為了保證在不同距離和角度都能正確對原始掃描數據進行分割，采用了自適應變閾值分割方法[10]。

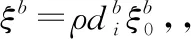
由區域分割得到k-1時刻的區域分割點集Ak-1={Ai,k-1|i=1,2,…,r1}和k時刻Bk={Bj,k|j=1,2,…,r2}，其中r1和r2為區域的個數。

2.2 多特征的相似度

為了提高ICP算法效率，利用區域特征信息用于匹配，可以大大減少計算量。由2.1節得到區域點集Ak-1和Bk，選擇每個區域的中心坐標(xc,yc)，角度α=arctan(yc/xc)，寬度w=|max{Δy}|，長度l=|max{Δx}|來表征區域的多特征信息。綜合考慮區域的多特征信息，只有與目標“相似”最大的那個區域被認為與其相匹配。

1)區域中心特征相似度

(2)

式中SDis為區域集Ak-1中第i個區域的中心坐標和區域集Bk中第j個區域的中心坐標的相似度。SDis越大，兩個區域就越靠近。距離最遠的區域相似度定義為0。

2)區域角度特征相似度

(3)

式中Sα為區域集Ak-1中第i個區域的角度和區域集Bk中第j個區域的角度的相似度。Sα越大，兩個區域就越靠近，角度差異最大的區域相似度定義為0。

3)區域長度和寬度特征相似度

(4)

(5)

式中SL和SW分別為區域長度和寬度特征的相似度。兩個區域之間的長度或寬度特征相似度越大，差異就越小，長度或寬度差異最大的區域相似度定義為0。

在得到區域的中心、角度、長度和寬度四個特征的相似度后，區域多特征的相似度為

(6)

2.3 特征相似度權重系數

式(6)在計算區域多特征相似度時，特征的權重系數是固定的，在復雜多變的環境中適應能力較差，為此，本文使用自適應特征相似度加權系數。

在每次掃描匹配時，根據初始權重系數，得到初始匹配區域集

C=(Cl=(Ai,k-1,Bj,k)|i=1,2,…,r1,

j=1,2,…,r2,l=1,2,…,r3)

(7)

式中l為匹配區域的個數，由C中匹配區域的中心坐標，經式(1)計算，得到相鄰兩組點集之間位姿變化Δx,Δy,Δθ。

區域集單項特征的變化量分別為

(8)

當特征變化較大時，應分配更小的權重系數，即，特征的權重系數與特征變化成反比。特征的權重系數為

(9)

2.4 同時定位與地圖構建

經匹配后，可以得到機器人k-1和k的位姿變換Δpk-1(Rk-1,Tk-1)。設以第1次掃描所建立的局部地圖M1作為全局的初始地圖[5]，第k次掃描時的局部地圖為Mk，機器人的位姿為pk，全局地圖為Mall，機器人的初始位姿為p1=(0,0,0)′。則第k次掃描時機器人的位姿pk為

pk=Δp1+…+Δpk-1

(10)

第k次掃描的局部地圖Mk坐標變換到全局地M′k為

M′k=Δp1+…+Δpk-1

(11)

全局地圖為

Mall=M1+M′2+…+M′k

(12)

3 仿真實驗驗證與分析

仿真中所采用的數據由悉尼大學發布的數據集，具有豐富的結構化和非結構化特點。為進一步研究算法的性能,分別用標準ICP匹配算法、本文算法對以上數據進行匹配。將標準ICP算法作為基準，從匹配誤差和迭代次數兩方面對以上兩種算法進行定量比較。

3.1 匹配誤差性能分析

分別用標準ICP算法和本文算法對匹配的誤差進行比較。從激光掃描數據集中隨機選取連續的 1000 幀數據，誤差以mm計算。結果如圖2所示。

圖2 匹配誤差對比

由圖2看出: 本文算法在匹配誤差上小于標準ICP算法。標準ICP算法考慮了所有的掃描點，甚至考慮了離群點，必然會導致對應點的誤匹配，影響匹配精度。本文算法主要是基于區域的自適應多特征進行匹配，明顯的提高了匹配精度。

3.2 迭代性能分析

分別用標準ICP算法和本文算法對迭代次數進行比較。從激光掃描數據中隨機選取連續的 1000 幀數據，將匹配的最大迭代次數均限制為50次。結果如圖3所示。

由圖3可以看出,本文算法在迭代次數上要遠遠小于標準ICP算法。標準ICP 算法的迭代次數是11.49; 本文算法的迭代次數5.34。標準ICP算法中對應點如果選取正確，迭代次數就會很少，如果對應點選取有誤，迭代次數就會很多。本文算法僅僅選取區域的中心點坐標來參與運算，減少了匹配的數據量，大大減少了運算次數。

圖3 迭代次數對比

3.3 地圖建圖結果驗證

用標準ICP算法跟本文算法分別進行定位與地圖構建，實驗對比結果如圖4所示。其中黑線為激光掃描儀的定位結果，周圍輪廓為建立的環境結構圖。可看出本文算法比標準ICP算法效果更好。

圖4 二種算法地圖建圖結果

4 結束語

針對標準ICP算法實現同時定位與地圖建圖計算量大的問題，本文采用了一種基于自適應多特征匹配的SLAM方法。利用區域的多特征用于匹配，可以大大減少計算量，然后，自適應調整多特征的加權系數從而保證ICP匹配的精度。通過以上實驗分析可以看出,本文算法在匹配誤差上要小于標準ICP算法,在迭代次數上遠遠少于標準ICP算法。因此，本文算法能夠有效地完成同時定位與地圖構建。