側風下高速列車臨界傾覆風速研究

劉榮，姚松，許嬌娥

側風下高速列車臨界傾覆風速研究

劉榮1, 2, 3，姚松1, 2, 3，許嬌娥1, 2, 3

(1. 軌道交通安全教育部重點實驗室，湖南 長沙 410075；2. 軌道交通安全關鍵技術國際合作聯合實驗室，湖南 長沙 410075；3. 軌道交通列車安全保障技術國家地方聯合工程研究中心，湖南 長沙 410075)

采用數值模擬方法計算橫風下高速列車的氣動力及力矩系數，利用EN14067的五質量模型研究橫風下車輛臨界傾覆風速曲線及不同參數對其傾覆的影響。研究結果表明：臨界傾覆風速隨著車速的增大而減小，隨著風向角的增大先減小后增大，最小值在 80°左右時出現，且隨著未平衡橫向加速度增大而減小。五質量模型中增加考慮的點頭力矩和搖頭力矩對臨界傾覆風速有一定影響，其中若不考慮點頭力矩，設置車輛臨界風速限制時偏高，對于車輛運行安全性有不利影響。一系懸掛和二系橫向剛度對傾覆系數影響不大。隨著二系垂向剛度增加，前轉向架輪對傾覆系數減小，后轉向架增大。橫向止擋間隙增大前后傾覆系數均增大。當抗側滾扭桿減小到原值60%以上時傾覆系數略有增大，幅度不超過10%。車輛質心越偏向車輛前端時，前傾覆系數增加，后傾覆系數減小。

高速客車；橫風環境；五質量模型；臨界傾覆風速

隨著列車發展趨向更高速度且輕量化。橫風下的列車氣動問題越顯突出，列車空氣動力學性能惡化，影響列車橫向穩定性，甚至可能使列車脫軌乃至傾覆[1?3]。世界上也多次出現由于強風作用導致列車事故的案例[4]。因此，研究大風條件下列車運行安全速度限值及影響因素是必需的。國內外學者提出了一些能夠評估鐵路車輛在傾覆風險方面的運行安全性的方法。“臨界傾覆風速”是評價列車橫風安全性的重要指標之一。國枝正春[5]提出了作用于車輛上外力的靜態平衡方程，即國枝正春式。日比野有等[6]在國枝式基礎上修正形成了更加詳細的詳細解析式法。Thomas等[7]運用多體仿真方法模擬研究了軌道彎曲、軌道不平順、車體橫移等影響因素對列車側風穩定性的影響。Baker等[8?10]采用動模型風洞試驗方法研究了列車橫風氣動特性，并通過靜態列車模型研究了擋風屏障對列車抗傾覆性能影響。歐洲標準EN14067中提出了計算列車特征風速曲線的方法：三質量方法，五質量方法(改進的準靜態方法)以及依靠時間域的多體系統動力學仿真方法。上述方法中常用的有詳細解析式法、三質量方法和多體仿真方法[11]。多體動力學仿真方法是目前相對來說考慮因素最全面，計算臨界風速最為準確的方法；詳細解析式法和三質量模型方法雖然簡單易推導、考慮因素較少，但是其計算簡便，容易定量把握要素影響；五質量模型方法相對來說考慮因素較為全面，更貼近實際，且相比多體動力學仿真方法要簡單，因此本文選取較少使用研究的五質量模型方法計算國內某型高速列車臨界傾覆風速，以及氣動力和車輛參數對列車運行傾覆性能的影響。

1 列車氣動性能數值模擬

1.1 高速列車數值計算模型建立

計算采用流體力學軟件STAR-CCM+進行數值模擬。為了與風洞試驗結果進行對比，采用一節半列車。模型列車周圍的局部區域、尾部的尾流區域、背風側區域等均加密網格，設置4個網格控制體，如圖1所示。采用RANS方法SST-模型，二階中心差分格式擴散項，對流項首先使用一階迎風格式進行離散，再采用二階迎風格式[12]。使用SIMPLE法耦合壓力?速度場，用迭代法修正壓力。計算給定空氣來流速度為60 m/s。

圖1 體網格模型截面

1.2 風洞試驗

為了確定數值模擬方法對高速列車側風安全性分析的適用性及檢驗數值模擬的準確性，將風洞試驗結果與數值模擬結果進行對比分析。在德國DNW風洞試驗中，列車模型簡化了轉向架，完整的幾何模型符合EN14067-6:2010要求。列車模型由一節頭車加一節中間車的一半組成，縮尺比例為1:15。模型試驗中測定了升力系數，阻力系數，側向力系數，俯仰力矩系數，側偏力矩系數等氣動力系數，計算公式如下：

式中：為大氣密度；0和0分別為列車參考面積和長度；i和M分別為列車所受相應氣動力和力矩；v為作用在車輛上的合成速度，在CFD模擬中也為相對于車輛的空氣來流速度。其可以分解為車速v和風速v，為風向角，而側滑角為車輛合成速度與車輛運行方向夾角，速度三角形如圖2所示。

圖2 速度三角形分解

將模型試驗與數值模擬的結果進行對比，表1為側滑角為10°時的結果對比。數值模擬與模型試驗的氣動力及力矩系數的誤差在10%以內，在工程誤差允許范圍之內。存在誤差的主要原因有：試驗模型的簡化(轉向架)，列車模型與地面相對運動的差異(地面效應模擬)，湍流模型以及數值計算采用的一些假設等。由此可見，數值模擬方法適用于計算氣動載荷系數。

表1 數值計算與試驗結果對比

1.3 CFD計算結果

通過對列車的氣動性能數值模擬仿真，得到了橫風下列車運行時的氣動力及力矩系數。不同側滑角(0°~90°)的側風環境下列車氣動力系數如圖3 所示。

圖3 列車氣動力系數

由圖3可以看出，除了點頭力矩變化規律較復雜，其他力/力矩系數變化規律簡單：側向力系數、傾覆力矩系數的數值大小均隨著側滑角的增大先增大后減小，且最大系數出現在70°左右。傾覆力矩主要與側向力大小有關，因此兩者變化規律相似。升力系數和搖頭力矩系數的絕對值大小隨著側滑角的增大先增大后減小，其數值最大出現在風向角為40°~50°左右。點頭力矩系數的變化規律比較復雜，其數值最大出現在風向角40°左右。

2 列車臨界傾覆風速計算方法

2.1 臨界傾覆風速定義

臨界傾覆風速是車輛受到橫風后開始發生側滾時的風速。假如車體受到橫風施加的外力，在最不利情況下，迎風側輪重達到一定臨界值，繼而若風速繼續增大則將引起車輛傾覆，將達到該臨界值時的風速定義為臨界傾覆風速。EN14067-6標準中將輪軌力相對于靜態輪軌力的減少值Δ和靜態輪軌力之比作為傾覆判定指標，且在減載率大于0.9時認為車輛運行有傾覆風險。

2.2 五質量模型方法

EN14067-6五質量模型方法(改進的準靜態方法)是一種考慮車輛主要部件運動學的靜態方法，不考慮減振器等引起的動態作用，得到的臨界風速一般小于多體動力學軟件方法得到的結果，偏保守。該模型適用于具有兩個轉向架且不考慮相鄰車輛或轉向架的車輛。本文研究的高速列車滿足該方法適用條件。

該方法采用耦合元件連接集中質量，模型(見圖4)共包括5個質量塊，車體(CB)、前轉向架(BG1)、后轉向架(BG2)和前后轉向架輪對(WS1，WS2)，一系和二系懸掛位于這些質量塊之間，構建為具有一定剛度的彈簧單元。此外若有抗側滾扭桿也應構建為位于車體和轉向架中間的具有繞軸旋轉剛度的扭桿。系統坐標如圖所示，方向為車輛運行方向，為車輛橫向，為垂向。車體具有5個自由度，沿和方向的平移和繞所有軸旋轉的自由度。轉向架具有3個自由度，沿和方向的平移和繞列車運行方向旋轉的自由度。輪對具有0個自由度。系統整體共有11個自由度。

在五質量模型建立中，需要計算不同工況下的車輛平衡位置，平衡位置需要由作用在車輛上的外力確定。在列系統方程組時，需要考慮的力和力矩有：質量力、彈性力和氣動力。質量力的計算與重力加速度和未被平衡加速度有關。彈性力的確定與變形量相關，除了一二系彈簧力之外，還應考慮車體和轉向架之間的抗側滾扭桿和止擋作用，金屬止檔的剛度應固定為1×108N/m，在止擋發生作用前的剛度應設置在0.5 mm的范圍內采用拋物線過渡。對于作用于車體的氣動力。不考慮氣動阻力作用，計算如下：

根據圖2中的合成速度圖，合成風速可以由風速、車速、風向與線路夾角計算得到。合成風速和側滑角計算公式如下：

考慮系統中所有質量體的11個自由度，設定車輛系統各剛體的位置矢量，有：

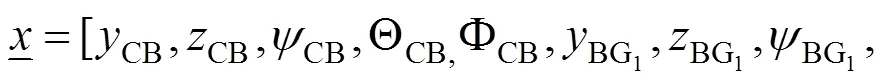
計算各個體上的力和力矩可以構建如下關于車體和轉向架力和力矩的系統平衡方程(輪對自由度為0)：

五質量模型的具體數學表達式推導參見文獻[11]。EN14067-6中規定應檢驗五質量方法的計算結果，應做檢驗，與標準附錄中列出的示例車輛的臨界傾覆風速曲線的計算進行對照，計算風向角為90°時得到的結果相對于示例車輛最大偏差應在±0.5 m/s內。本文中的計算方法與標準附錄算例進行對比后，結果符合要求。

3 列車臨界傾覆風速曲線

利用五質量模型方法對車輛進行傾覆計算，得到了不同風速、不同運行速度和不同風向角下高速列車的傾覆系數。為防止車輛傾覆，借助高速列車運行安全性標準，在EN-14067.6中規定傾覆系數D ＜0.9時車輛安全，以0.9作為臨界值從而確定臨界傾覆風速曲線。

圖5 臨界傾覆風速隨車速變化曲線

圖6 車速為200 km/h時臨界傾覆風速隨風向角變化曲線

圖5是風向角為90°時不同未被平衡橫向加速度下(a=0，a=0.5 m/s2,a=1 m/s2)列車臨界傾覆風速隨車速變化曲線。可以看出隨著車速增加臨界傾覆風速下降，在車速在80~100 km/h之間，CWC值迅速下降，而當速度大于100 km/h 時，CWC下降速度減慢。且在未被平衡橫向加速度方向為正時，隨著其增大，列車臨界運行安全速度減小，不同未被平衡橫向加速度下CWC曲線變化規律相同。圖6是車速為200 km/h時列車臨界傾覆風速隨著風向角變化曲線，可以看出CWC曲線最小值出現時的風向角并不是垂直于列車運行方向，而是在=80°。原因是由于側風作用下列車所受氣動系數的特性，對車輛傾覆影響最大的是側向力和傾覆力矩，而其系數的最大數值點不是在90°時出現，當列車以200 km/h運行時，隨著風向角增大，相對于列車的偏航角也增大，但臨界角度對應的系數 減小。

4 不同參數對列車傾覆特性影響

4.1 點頭力矩和搖頭力矩影響

在運用較多的詳細解析式法和三質量模型方法中，考慮造成列車傾覆的氣動力和力矩時，只考慮了側向力、升力和傾覆力矩，由于靜態模型不考慮列車運行，運行方向的阻力不被考慮。而在五質量模型方法中，不僅考慮了這3個力和力矩，點頭和搖頭力矩也同時被考慮。因此對比分析了點頭力矩和搖頭力矩對臨界傾覆風速曲線的影響。

圖7是不考慮點頭或搖頭力矩時臨界風速變化對比。可以看出，不考慮搖頭力矩時，臨界風速值變化不大。在車速小于200 km/h時，該條件下臨界風速小于正常考慮力矩，車速大于200 km/h時，該條件下臨界風速稍大于考慮全力矩時，但相差很小。不考慮點頭力矩時，臨界風速值變化較大，在車速小于100 km/h時，該條件下臨界風速稍小于考慮全力矩時，車速大于100 km/h時，該條件下臨界風速大于正常考慮力矩情況，且相差最大值達2.2 m/s。當點頭力矩和搖頭力矩均不考慮時，臨界傾覆風速與正常考慮力矩時相差最大值達2.5 m/s。總體來說是否考慮搖頭力矩對臨界傾覆風速曲線影響很小，而車速較高時，點頭力矩對臨界傾覆風速曲線有一定影響。說明詳細解析式法或三質量模型方法中不考慮搖頭力矩的作用有一定合理性。但考慮點頭力矩更合理。不考慮點頭力矩時臨界傾覆風速較高，對車輛運行安全有不利影響。

4.2 車輛參數影響

車輛結構參數尤其懸掛參數對列車動力學性能有重要影響，尤其是在側風下運行的列車，車輛產生大幅振動，合適的車體參數能很好的防止列車偏移，保證列車運行安全性。一系懸掛系統能實現輪對的彈性定位，二系懸掛系統能提高轉向架平穩性且抑制蛇形運動。因此優化車輛動力學性能，需要考慮各車輛結構參數對其動力學性能的影響。改變某個參數并保持其他參數不變，分析不同車體參數對車輛系統動力學性能的影響。

(a) 不考慮搖頭力矩；(b) 不考慮點頭力矩；(c) 不考慮搖頭力矩和點頭力矩

由于有些車輛參數的變化對臨界傾覆風速的影響不明顯，因此以判別車輛臨界狀態的傾覆系數作為目標結果。考慮五質量車輛模型中的關鍵特征參數，選定了7個車輛參數進行分析，分別是：一系垂向/橫向剛度、二系垂向/橫向剛度、二系橫向止擋間隙、抗側滾扭桿剛度、及車輛偏心。由于各參數的量綱差異，為統一比較其對車輛傾覆系數的影響程度，使指標值的變化具有可對比性，在分析過程中將車輛各原參數作為比較基準，以參數變化率為橫坐標分析變化情況。設定各參數在原值上增減90%，每隔10%取一個值，其中車輛偏心值過大不符合實際情況，因此考慮車輛偏心范圍在±1 m以內。由于環境風速和列車速度工況較多，取車速為200 km/h，風速取25 m/s，未被平衡橫向加速度為0，風向角為90°時，計算車輛參數變化對傾覆系數的影響。在五質量模型中，前后轉向架輪對的傾覆系數被分開考慮，以較大的傾覆系數值作為傾覆判斷值。

圖8分別為不同車輛參數變化對車輛傾覆系數的影響。可以看出風速為25 m/s時，由于此時合速度作用下的搖頭力矩對車輛影響較大，因此原車輛參數下所計算的列車前轉向架輪對傾覆系數比后傾覆系數大，且約高出0.1左右，也說明以單個轉向架的傾覆系數作為判別指標的合理性。可以看出一系懸掛參數變化對傾覆系數無明顯影響，其中一系橫向剛度在其減小量大于70%時傾覆系數略有增大。二系懸掛參數中二系橫向剛度減小對傾覆系數的影響很小，其增大時后轉向架輪對傾覆系數稍有減小。二系垂向剛度影響較大，隨著二系垂向剛度的減小，前轉向架輪對傾覆系數增大，后轉向架輪對傾覆系數減小，且參數減小到60%時，變化曲線斜率絕對值增大。橫向止檔自由間隙變化對傾覆系數有一定影響，隨著間隙增大前后轉向架輪對傾覆系數均增大，當間隙大于原值時，后轉向架輪對傾覆系數變化不大。抗側滾扭桿剛度變化的影響不大，在抗側滾扭桿剛度減小到原值的60%以上時傾覆系數略有增大，增幅不超過10%。另外車輛偏心對車輛傾覆系數有較大影響，變化率為正時表示車輛質心偏向車輛前端，隨著車輛越向前端偏心，前轉向架輪對的傾覆系數增加，后轉向架輪對的傾覆系數減小。

(a) 一系橫向剛度；(b) 一系垂向剛度；(c) 二系橫向剛度；(d) 二系垂向剛度； (e) 橫向止檔間隙；(f) 抗側滾扭桿剛度；(g) 車輛偏心

5 結論

1) 臨界傾覆風速隨著車速增加而減小，且隨著橫向加速度的增大而減小，但曲線變化規律相同。隨著風向角的增大(0°~90°)臨界傾覆風速先增大后略有減小，曲線最小值出現在風向角為80°左右。

2) 五質量模型算法較為全面的考慮了靜態車輛計算所需的氣動力，增加考慮了點頭和搖頭力矩的影響。若不考慮搖頭力矩，當車速小于200 km/h時，臨界風速小于考慮全力矩時，車速大于200 km/h時，該條件下臨界風速變大。點頭力矩對臨界傾覆風速影響較大，在車速小于100 km/h時，該條件下臨界風速稍小于考慮全力矩時，車速大于100 km/h時，該條件下臨界風速變大，且相差最大值約達 2.2 m/s。

3) 通過五質量模型算法計算了不同車輛參數對車輛傾覆系數的影響。一系剛度和二系橫向剛度對傾覆系數影響較小。隨著二系垂向剛度增加，前轉向架傾覆系數減小，后轉向架傾覆系數增大。隨著二系橫向止檔間隙增大前后轉向架傾覆系數均增大。抗側滾扭桿影響較小，當其減小到原值的60%以上時傾覆系數略有增大，幅度變化不超過10%。若車輛偏心時質心越偏向車輛前端，前轉向架傾覆系數隨之增加，后轉向架傾覆系數減小。說明在計算列車臨界傾覆風速時，應重點分析二系垂向剛度、橫向止擋間隙和車輛偏心等因素的影響。

[1] 高廣軍, 田紅旗, 姚松, 等. 蘭新線強橫風對車輛傾覆穩定性的影響[J]. 鐵道學報, 2004(4): 36?40. GAO Guangjun, TIAN Hongqi, YAO Song, et al. Effect of strong cross-wind on the stability of trains running on the Lanzhou-Xinjiang railway line[J]. Journal of the China Railway Society, 2004(4): 36?40.

[2] 劉加利, 于夢閣, 張繼業, 等. 基于大渦模擬的高速列車橫風運行安全性研究[J]. 鐵道學報, 2011, 33(4): 13?21. LIU Jiali, YU Mengge, ZHANG Weihua, et al. Study on running safety of high-speed train under crosswind by large eddy simulation[J]. Journal of the China Railway Society, 2011, 33(4): 13?21.

[3] Andersson E, Haggstrom J, Sima M, et al. Assessment of train-overturning risk due to strong cross-winds[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2004, 218(3): 213?223.

[4] 葛盛昌. 新疆鐵路風區大風天氣列車安全運行辦法研究[J]. 鐵道運輸與經濟, 2009, 31(8): 32?34, 84. GE Shengchang. Study on train safety operation method in the Xinjiang railway under cross wind[J]. Railway Transport and Economy, 2009, 31(8): 32?34, 84.

[5] Kunieda M, Theoretical study on the mechanics of overturn of railway rolling stock[R]. Railway Technical Research Report, 1972(793): 1?15.

[6] 日比野有, 石田弘明.車両の転覆限界に関する靜解析式法[J].鉄道総研報告, 2003, 17(4): 39?44. Hibino Tamotsu, Ishida Hiroaki. On the static analysis method for the limit of covering[J]. Report of Railway, 2003, 17(4): 39?44.

[7] Thomas D, Diedrichs B, Berg M, et al. Dynamics of a high-speed rail vehicle negotiating curves at unsteady crosswind[J]. Journal of Rail and Rapid Transit, 2010(224): 567?579.

[8] Baker C J. The wind tunnel determination of crosswind forces and moments on a high speed train[M]. Berlin: Springer- Verlag Berlin Heidelberg, 2002.

[9] Baker C J. The behaviour of road vehicles in unsteady cross winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993(49): 439?448.

[10] Baker C J. Ground vehicles in high crosswinds parts I: Steady aerodynamic forces[J]. Journal of Fluids and Structures, 1991(5): 69?90.

[11] EN 14067-6: 2010, Railway applications-aerodynamics- part 6: Requirements and test procedures for cross wind assessment[S].

[12] 王福軍. 計算流體動力學分析[M]. 北京: 清華大學出版社, 2004: 210?215. WANG Fujun. Analysis of computational fluid dynamics [M]. Beijing: Tsinghua University Press, 2004: 210?215.

Study on critical overturning wind speed of high-speed train under cross wind

LIU Rong1, 2, 3, YAO Song1, 2, 3, XU Jiaoe1, 2, 3

(1. Key Laboratory of Traffic Safety on Track, Central South University, Ministry of Education, Changsha 410075, China;2. Joint International Research Laboratory of Key Technology for Rail Traffic Safety, Changsha 410075, China; 3. National & Local Joint Engineering Research Center of Safety Technology for Rail Vehicle, Changsha 410075, China)

The aerodynamic coefficients of high-speed train under crosswind were calculated by numerical simulation method. The five-mass model of EN14067 was used to study the critical overturning wind speed curve of vehicles under crosswind and the influence of different parameters on its overturning. Results show that: the critical overturning wind speed decreases with the increase of vehicle speed, critical overturning wind speed first decreases and then increases with the increase of wind direction angle, and the minimum value appears at about 80°, and decreases with the increase of unbalanced lateral acceleration. The shaking moment and nodding moment have a certain impact on the critical overturning wind speed, If the nodding moment is not taken into account, the critical wind speed limit of the vehicle will be set higher, which has a negative impact on the safety of the train operation. The primary suspension parameters and the second lateral stiffness have little effect on the overturning coefficient. With the increase of the vertical stiffness of the secondary system, the overturning coefficient of the front bogie wheel set decreases and that of the rear bogie increases. With the increase of lateral stop clearance both overturning coefficients increase. When the anti-roll torsion bar is reduced to more than 60% of the original value, the overturning coefficient increases slightly, and the range is not more than 10%. When the centroid of the vehicle leans towards the front end of the vehicle, the overturning coefficient of the front bogie wheel set increases and the overturning coefficient of the rear bogie wheel set decreases.

high-speed train; crosswind environment; five-mass model; critical overturning wind speed

U271.1

A

1672 ? 7029(2019)11? 2643 ? 08

10.19713/j.cnki.43?1423/u.2019.11.001

2019?02?26

國家重點研發計劃資助項目(2016YFB1200506-03)

姚松(1975?)，男，湖北公安人，教授，博士，從事軌道交通安全研究；E?mail：song_yao@csu.edu.cn

(編輯 蔣學東)