一元一次方程應用題解法歸類

一、數字問題

例1 有一個兩位數，兩個數位上的數字和是10，如果把個位與十位上的數字對調，那么所得的兩位數比原來的兩位數大54，求原來的兩位數。

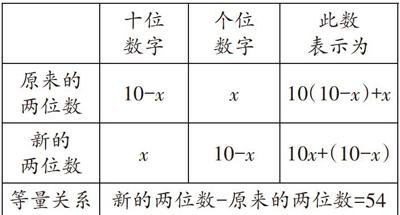
【分析】設原來的兩位數個位上的數字為x，則根據題意，有：

[ 十位

數字 個位

數字 此數

表示為 原來的

兩位數 10-x x 10（10-x）+x 新的

兩位數 x 10-x 10x+（10-x） 等量關系 新的兩位數-原來的兩位數=54 ]

對于數字問題，最常見的就是已知一個多位數，然后每個數位上的數字進行位置變換后，得到一個新的數字。新的數字與原來的數字有數量關系，這是解決這類題目的關鍵。一般將一個數各數位上的數字設成未知數后，如果要表示這個數，十位上的數字要乘10，百位上的數字要乘100，以此類推。

二、分配問題

例2 某制衣廠計劃若干天完成一批服裝的訂貨任務。每天生產20套服裝，就比訂貨任務少100套;每天生產23套服裝，就可超過訂貨任務20套。問這批服裝的訂貨任務是多少套？

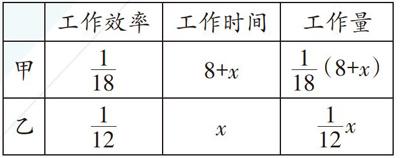
【分析】設計劃x天完成這批服裝，由題意，我們可以畫出如下分析圖：

所以可得23x-20=20x+100。

對于分配問題，要弄清楚兩次分配方法下的生產數量與訂貨任務之間的關系，解決的關鍵是找到兩次分配方法下的生產數量之間的關系，即等量關系。像這類問題，用畫線段圖的方法較為直觀。

三、配套問題

例3 某車間有22名工人生產螺釘和螺母，每人每天平均生產螺釘1200個或螺母2000個，一個螺釘要配兩個螺母。為了使每天生產的產品剛好配套，應該分配多少名工人生產螺釘？多少名工人生產螺母？

【分析】設分配x名工人生產螺釘，則生產螺母的人數為（22-x）名，生產螺釘1200x個，生產螺母2000（22-x）個。……