假設性思維在中考選擇和填空題中的應用分析

摘 要：選擇題和填空題在中考試題中所占的比重不是很大，但是學生在考試時又不能不要這些分數，不僅如此，還要盡可能地拿到選擇題與填空題的所有分數。因此，教師在平時的教學工作中，要向學生滲透假設性思維的教學，讓學生能夠在考試的過程中運用起來，盡可能地拿到更多的分數。那么，教師應該怎樣在教學中向學生滲透假設性思維呢？本文將圍繞這一問題，根據個人經驗以及近年來層出不窮的理論研究成果，結合實際情況，進一步展開論述。

關鍵詞：假設性思維;選擇題;填空題;應用方法;教學方法

假設性思維，簡單來說，就是學生通過假設與猜想去完成解決問題的過程，能夠高效地完成相對簡單的問題，但假設性思維也不是胡亂猜想，要根據題目中所給出的要素進行猜想。眾所周知，數學在是一門基礎學科，在中考中占有很大的比例，其重要性也由此可見一斑。因此，教師要在教學的過程中，幫助學生采用更加科學、合理的手段去解決問題，從而使學生能夠在中考時能夠以最高的效率完成選擇題與填空題。

一、 假設性思維激發學生的解題興趣，發揮學生主體性

興趣是學生在進行任何科目學習時的基礎動力來源，也是直接影響學生學習成果的重要非智力因素之一，在學生做題的過程當中更是如此。鑒于此，教師要教會學生去利用假設性思維尋找解題的樂趣，才能讓學生善于解題。我們都知道，猜想活動具有強烈的創造性，學生在解題時使用這種猜想的方法會產生激烈的思維活動，讓學生的思維“活”起來，使學生在解決同一問題的過程中從多角度、多方面進行思考，在經過反復琢磨后，得到最佳答案。在中考的試題里，選擇題以及填空題與其他題型的類型不同，相較于大題，選擇填空只注重結果，而大題還需要將解題過程做到完善。因此，在日常的教學當中，教師就需要運用假設性思維幫助學生訓練快速解題的能力，來應對考試。

例如，在進行多邊形的相關內容教學時，教師可將2019年河北省數學中考真題第一題：下列圖形為正多邊形的是（ ?）

A. ?B. ?C. ?D.

將此題運用于課程的講解中，讓學生去猜測正多邊形的概念。教師提出要求：“同學們知道這道選擇題怎么解嗎？”一名學生站起來說道：“正多邊形是什么意思呢？”教師：“大家可以猜測一下正多邊形的概念是什么？”學生：“根據以前學過的正方形的基本特征，我猜是每條邊都一樣長的多邊形叫做正多邊形。”教師在此時可以不表明學生觀點的正確與否，留下懸念，學生為了驗證自身假設的正確性，自然而然就會關注教師的講解、關注數學課堂。之后，教師逐步為學生進行講解“正多邊形”的概念，與學生做出的假設相同。回到題目，根據正多邊形的概念，能夠輕易的得出這道問題的答案是B。學生通過題干做出假設，解決了選擇題，這種能力會隨著時間的推移逐步烙印在學生的腦海中，從而能夠靈活地運用假設性思維解決試卷中的選擇題。

二、 驗證假設引發學生的高度關注，集中學生注意力

在上文中提到了教師在教學的時候，利用選擇題引導學生猜測數學概念的過程，而在驗證學生假設的過程中，教師不難發現，學生的注意力非常集中，因此，想要進一步教會學生運用假設性思維去解決試卷中的選擇題與填空題，就需要在驗證學生假設的過程中做文章。我們都知道，學生一旦升入初中，他們的心理會產生非常大的變化，由幼稚好動逐漸變得成熟穩重，但是，唯一沒有變的是學生的好奇心，這種好奇心在驗證自身假設與猜想時表現的尤為明顯。因此，教師要將學生的這種心理狀態利用起來，通過教師的循循善誘，讓學生在不知不覺中進入學習狀態，雖然學生在課堂中注意力高度集中的時間是有限的，但教師不妨使用這種方法去將這段時間盡可能地延長，從而使學生能夠將假設性思維更靈活地運用在解決試卷中選擇填空題中。

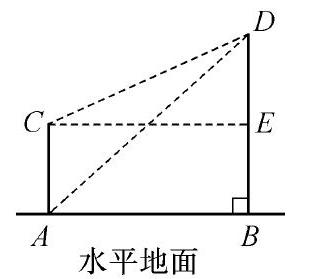
例如：在進行“仰角”相關內容教學時，教師可將這道真題設置在課堂教學當中：如圖，從點C觀測點D的仰角是（ ?）

A. ∠DAB B. ∠DCE C. ∠DCA D. ∠ADC

將這道題目運用在課堂教學中，讓學生猜測仰角的概念。教師：“仰角的相關題目在數學試卷中非常常見，不僅如此，仰角與我們的生活也息息相關，同學們能夠開動腦筋，猜一猜仰角的概念嗎？”學生：“仰角就是抬頭看的時候，視線和地面的夾角，對嗎？”教師在學生假設正確的時候切忌將問題的正確答案公布，要在學生心中保留疑問，也就是“吊胃口”，讓學生有興趣去緊跟教師的講解，通過逐步的推理、引導去獲得問題的答案。在驗證學生猜想的過程中，教師要擁有較好的口才，讓學生將驗證自身猜想的過程變成一種樂趣。這樣一來，學生就能夠將枯燥抽象的數學知識通過假設性思維轉變的生動起來，從而能夠在做題的過程中更好地使用假設性思維。

在文章的一、二兩點中，教師在課堂教學中穿插中考真題的假設與驗證，主要目的是為了讓學生習慣假設性思維，并能夠對假設性思維的解題技巧有初步的認識，并在腦海中形成初步的運用方法。那么，學生在實際做題的過程中，又要怎樣運用假設性思維呢？接下來，展開進一步論述。

三、 分析假設指導學生的猜想方向，消除解題盲目性

分析假設，顧名思義，就是學生經過對題干數據的分析后，根據分析得出的結論進行合理假設的過程。使用這種方法時，所面對的題目一般來說比較復雜，往往存在多種情況，學生在進行分析過后，通過對比，并得出在某些前提下的某種情況應該怎樣做的結論，而后從問題出發，回推題干，看是否能夠將結論與題干、問題三者互相吻合。同時，也要將經過分析推理出的另外幾種情況與正確答案進行對比，從而能夠將隱藏在問題中的隱藏前提挖掘出來。這種分析假設的方法比較高級，對學生的解題能力、認知水平、數學知識積累程度均有非常高的要求。因此，教師要在平日的學習中要求學生注意積累，并要求學生在使用分析假設時格外小心謹慎，切忌將多種前提下的不同結果混淆，從而造成不必要的失分，進一步提升學生在選擇填空題目中的正確率。

仍以第二大點中的選擇題為例。

在這道問題中，題目要求的是學生在點C觀測點D時的仰角，雖然教師在課堂中已經將與仰角相關的知識點傳授給學生，但學生很可能存在理解不透徹的情況，非常容易將答案選為D，即∠ADC。但若學生能夠將假設性思維運用在這道題目的解題過程中，就能通過聯想，將答案分為多種情況去進行分析。首先，在其他兩個選項中，有著非常明顯的錯誤，故而不予考慮，在容易混淆的兩個選項當中，學生假設∠ADC為從點C觀測點D的仰角，學生就能夠根據自己的實際生活經驗去推測，能夠將仰角的定義推測出來。“我在觀測另一個點時，視線與地面的夾角就是仰角。”再將∠ADC反推到題目中，學生會發現，∠ADC的AD邊與DC邊沒有一條是與地面平行的，從而得出D選項，∠ADC的答案是錯誤的。而反觀∠DCE，CE邊與地面平行，且DC邊與地面的平行線CE相交，因此，選項B，∠DCE是正確的。

四、 類比假設磨煉學生的創新能力，尋找解題新方法

類比假設是通過對比兩個類型相似的題目，去得到兩個題目的正確答案。這種方法對學生抓問題本質的能力要求相對較高，能夠通過不同形式的題干找到題目與題目之間的相似點，從而將兩道或更多道題目在保證正確率的前提下用最短的時間完成這些題目的解答過程。

數學的本質就是一個不斷進行類比性假設，并在類比中推導新的結論、找到新方法的過程，在中考解題方面，更是如此。因此，教師在進行中考解題教學的過程中，教師要有意識地將題目類型相似或相同的問題以組合的形式讓學生去完成，并要求學生運用假設性思維去完成相應的題目。在學生解題的過程中，教師要走進學生當中，去收集學生對多道題目的假設思路，從而能夠對學生的想法進行更具針對性的講解，讓學生在類比假設的過程中去感受類型相似題目之間的區別，從而能夠產生劇烈的思維活動，產生更加新穎的解題方式，鍛煉學生的創新能力，使學生能夠在解題的過程中不斷發現新知識、新方法，在經過長時間的鍛煉之后，學生的數學思維會得到長足進步，他們的假設性思維也會得到進一步發展。

五、 歸納假設尋找解題的隱藏線索，提高解題的準確性

歸納假設是學生通過對不同種類題目類型的假設，去找到這些類型題目中普遍存在的可用線索，從而進一步提升學生的假設性思維。在使用歸納假設法時，對學生的歸納總結能力要求較高，也就要求了教師在解題教學的過程中，著手提升學生的聯想能力，讓學生通過聯想的方法，對多種題目類型進行總結與歸納，從而進一步提升學生的解題效率。

在中考重點題目中，會出現很多“同底數冪的乘法法則”的相關內容，其運用非常廣泛，在很多題目中都會涉及。在進行解題教學時，教師可以將“同底數冪的乘法法則”的推導方式演變而成的歸納假設法向學生傳授。也就是，在這一則算式：133×132=（13×13×13）（13×13）=135中，經過歸納的方式，能夠得出結論：a3×a2=（aaa）（aa）=a5也就是“同底數冪的乘法原則”公式。教師將這種思想有意識的灌輸給學生，讓學生在做題的過程中也能通過“找規律”的方式歸納出題目中所存在的隱藏線索，從而進一步提升學生的歸納假設能力。

綜上所述，教師引導學生將假設性思維運用于中考選擇填空題的解答時，首先要通過假設性思維引導學生對問題的答案提出猜想，讓學生對自身猜想的正確性產生好奇心，從而使學生對假設性思維解題初步產生興趣;其次，要利用學生的這種好奇心，在驗證假設正確性的過程中調動學生的注意力，延長數學課堂的有效時間;使用這兩種方式幫助學生初步培養假設性思維，讓學生能夠在解題中將其運用起來。在實際解題過程中，教師首先要向學生傳授分析假設的方法，讓學生能夠將題目中的多種情況注意分析，從而得到最佳答案，提升解題準確性;其次，通過類比假設法，讓學生找到相同類型題目之間的共性，從而提升解題速度;最后，通過歸納假設法，幫助學生提升總結歸納的能力，使學生能夠在解題的過程中找到題目中的隱藏線索。

參考文獻：

[1]汪彥那.邏輯推理素養引領下的“猜想—論證”式初中數學教學設計研究[D].重慶：重慶師范大學，2019.

[2]曾金生.初中數學教學中的猜想思維分析[J].名師在線，2019（5）：64-65.

[3]張天富.由初中數學假設法教學引發的思考[J].數學學習與研究，2017（20）：136.

[4]陳鋒.讓“猜想”植根于初中數學教學[J].內蒙古教育，2016（35）：76.

作者簡介：

鄭衛強，浙江省杭州市，浙江省杭州市余杭區崇賢中學。