基于斷裂及高溫損傷的巖石蠕變模型研究

李修磊，李起偉,2，李 倩

(1.重慶交通大學交通運輸學院，重慶 400074；2.中交第一公路勘察設計研究院有限公司，陜西 西安 710075；3.四川大學錦江學院，四川 眉山 620860)

隨著深部資源的開采(如油井、氣井、礦井、地熱等)，深埋硐室開挖以及高放射核廢料深埋處置等深部地下工程已逐漸向地下延伸數千米[1-2]，這些工程往往處于高溫、高應力環境，盡管初始階段呈穩定狀態，但由于長時間巖石的蠕變作用可能導致圍巖變形發生破壞。因此，研究巖石在長時間溫度-應力耦合作用下的蠕變力學行為和變形規律，對工程的穩定性具有重要的意義[3-4]。

關于巖石溫度效應的蠕變性能研究，已有相關試驗開展。Chopra等[5]采用高分辨率氣體介質的試驗裝置，研究純橄欖石在圍壓為300 MPa、2種溫度分別為1 100℃和1 300℃下的蠕變特性，試驗發現高溫、高應力下橄欖石的蠕變行為可用Burgers模型進行描述。Kinoshitan等[6]通過試驗研究了花崗巖在20～100℃下單軸蠕變特性，結果表明溫度的升高能夠加速花崗巖的蠕變破壞。Chen等[7]單軸和三軸蠕變試驗結果表明，花崗巖的時效破壞與其斷裂過程所引起的損傷演化密切相關；相同加載應力下，圍壓的增加能夠降低應變速率，延緩破壞時間；相同圍壓條件下，溫度和應力水平的升高不會對花崗巖破壞時裂紋擴展形態有顯著影響，但會加快裂紋擴展的速度，進而縮短蠕變破壞時間。劉泉聲等[8]針對三峽花崗巖開展了20～300℃范圍內的單軸和三軸蠕變試驗，給出了花崗巖蠕變特性隨溫度的變化規律。張強勇等[9]研究了不同溫度下片麻狀花崗巖的三軸蠕變特性，試驗結果表明，片麻狀花崗巖存在蠕變應力閾值，且受溫度和圍壓的雙重影響；中、低應力條下，巖石只發生減速和等速蠕變；高應力條件下巖石會出現加速蠕變過程；溫度升高會導致巖石的蠕變速率增大，應力閾值越低，蠕變破壞時間越短。張寧等[10]和陳亮等[11]分別對魯灰花崗巖和北山花崗巖的蠕變特性進行了試驗研究，溫度和應力水平都會影響巖石的蠕變特性。上述試驗成果為建立巖石的蠕變本構關系奠定了良好基礎。

目前，國內外已有學者考慮溫度效應的巖石蠕變本構關系理論研究。如，Chen[12]等采用西原模型對花崗巖蠕變特性進行了描述，分析了加速蠕變階段損傷演化規律，建立了各模型參數與溫度之間函數關系；唐皓等[13]和曹麗麗等[14]分別基于函數階微積分理論建立了適用于鹽巖和泥巖的函數階蠕變本構模型。胡其志等[15]基于廣義Bingham模型在蠕變衰減和穩態蠕變階段引入非線性函數，對加速蠕變過程進行損傷劣化分析，建立了考慮溫度的鹽巖損傷蠕變本構模型；王春萍等[16]建立了溫度-應力耦合作用下的西原模型，并用試驗結果進行了驗證；張強勇等[17]基于不同溫度、不同應力水平下片麻花崗巖的三軸蠕變試驗結果，建立了熱力耦合作用的熱黏彈塑性損傷蠕變模型，提出了高、中、低應力狀態下溫度對片麻花崗巖蠕變特性的影響規律；梁玉雷等[18]考慮溫度變化周期對巖石蠕變的影響，建立了適合描述大理巖的熱力耦合的改進Burgers模型；Xu等[19]基于熱力學原理，建立了溫度-應力耦合作用下脆性巖石的蠕變損傷模型，并以最大拉應力和摩爾庫倫準則作為單元破壞準則，在有限元軟件Comsol的基礎上對模型進行二次開發，較為準確地模擬了不同溫度條件下花崗巖典型的三階段蠕變變形全過程。

由以上分析可知，現有考慮溫度作用的巖石蠕變模型大多是在經典蠕變模型的基礎上，根據不同溫度的試驗結果建立模型參數與溫度的函數關系，進而提出了考慮溫度效應的巖石蠕變本構關系。根據文獻[11]，巖石的蠕變破壞與裂紋起裂、擴展引起的損傷變化有關，而現有蠕變模型中并沒有考慮外力作用下巖石內部裂紋擴展引起的損傷演化。為此，本文將基于巖石斷裂理論，考慮裂紋擴展引起的損傷，推導熱力耦合作用下的一維損傷蠕變方程，并將其推廣到三維應力狀態，采用非線性最小二乘法確定模型參數，進而利用不同溫度下花崗巖的蠕變試驗結果驗證本文模型的適用性和合理性。

1 應力與裂紋擴展之間的關系

圖1給出了脆性巖石單元體微裂紋擴展的細觀力學模型[20]，假定巖石為各向同性彈性材料，單個初始裂紋的長度為a，初始裂紋與主應力σ1方向的夾角為β，巖石所受圍壓σ2=σ3。

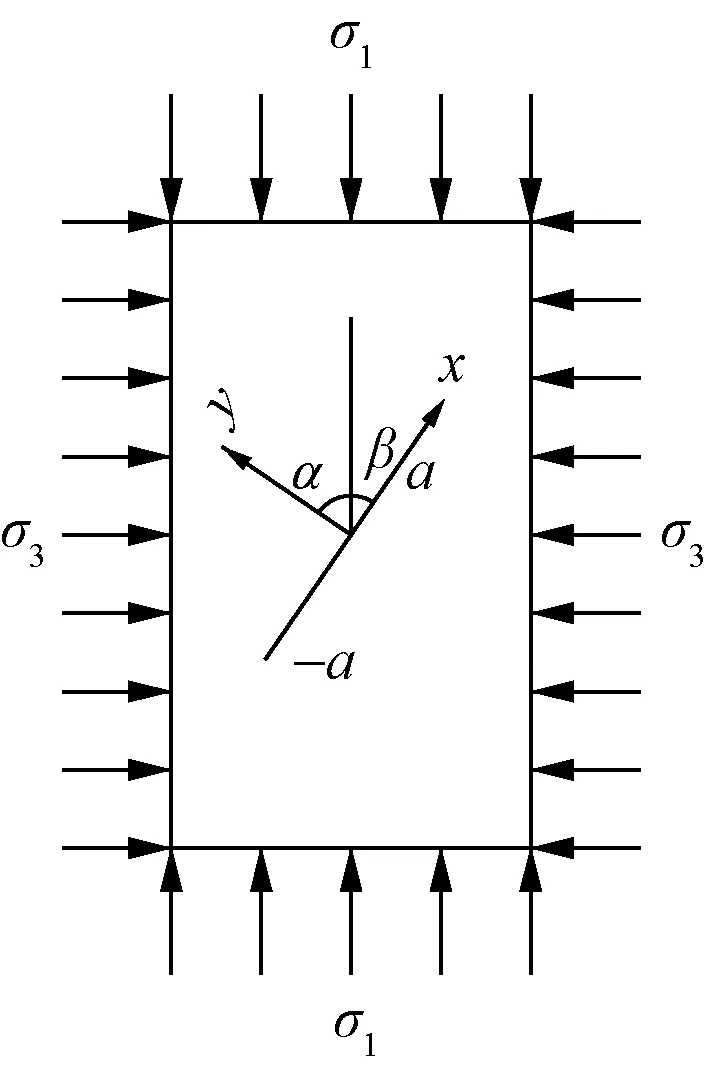
圖1 壓力作用下裂紋擴展力學模型

利用莫爾圓(圖2)，得到應力作用下裂紋表面的正應力σn和剪應力τ分別為：

(1)

(2)

當外部應力大于臨界應力σ1C(也就是說，裂紋表面的剪應力τ大于材料固有的抗剪切強度τ0)時，翼型裂紋開始產生；當外部應力小于臨界應力σ1C，沒有翼型裂紋的產生。

圖2 摩爾-庫倫模型

材料固有的抗剪切強度τ0為：

(3a)

對于單軸壓縮試驗，τ0為：

(3b)

式中：φ——內摩擦角；

C0——無側限抗壓強度。

在常規三軸試驗中(圖1)，由應力分量坐標變換，遠場的應力狀態為：

(4)

(5)

σs=σ1C-σ3

(6a)

單軸應力狀態下的屈服應力為：

(6b)

式中：σs——屈服應力或稱為臨界損傷應力。

2 巖石熱黏彈塑性蠕變損傷模型

根據不同溫度下巖石的蠕變試驗結果[17]，發現巖石的蠕變過程具有時效性(圖3，其中分級加載應力差σ1-σ3分別為160，180，200，220和240 MPa)，具體特征如下：加載過程中巖石會發生瞬時應變增量；低應力水平下巖石發生減速和等速蠕變，變形隨時間趨于穩定；高應力水平下(應力超過臨界值)時，巖石除了有減速和等速蠕變，還會發生加速蠕變，為典型的非線性蠕變行為。巖石的蠕變特性以及相應的力學參數與其受到的溫度和外部應力密切相關。

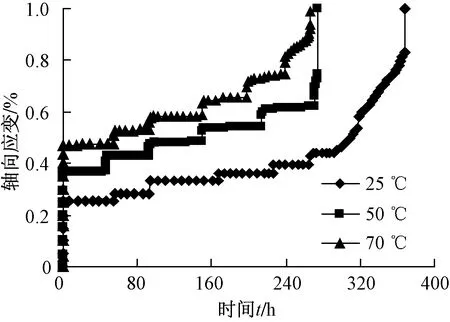
圖3 不同溫度下片麻花崗巖的軸向蠕變曲線(σ3=30 MPa)[17]

巖石經典的蠕變模型(如Kelvin模型、Bingham模型、Burgers模型和Nishihara(西原)模型等)僅能反映蠕變變形的瞬時和穩定階段[21]，無法有效考慮溫度和應力耦合作用下巖石蠕變變形的全過程。目前，多數試驗結果[7,11,22]證實，加速蠕變階段的發生主要與巖石內部微裂紋擴展的損傷演化有關。基于此，本文將結合常用的Burgers模型和西原模型引入巖石的斷裂損傷，并考慮溫度和應力的耦合(圖4)。

圖4 模型元件的組成

改進后的本文模型可看作是在Burgers模型的基礎增加了1個考慮損傷的黏塑性元件，也可看作是在西原模型的基礎上增加了1個串聯的牛頓黏壺元件。

2.1 熱-黏塑性損傷元件

近些年，已有試驗研究成果表征了巖石的損傷演化過程[23-24]。結果表明，蠕變試驗過程中巖石的損傷演化可以用負指數函數來表征[12,17]：

D=1-exp(-αt)

(7)

式中：D——損傷變量，由0逐漸趨近于1，分別對應著初始和完全損傷狀態；

α——與損傷演化過程相關的參數。

本文研究中將采用式(7)來模擬隨時間變化的巖石內部裂紋擴展引起的損傷演化過程。

Li等[25]的試驗數據證實只有當施加的應力達到一定程度和超過某一閾值時，巖石才會發生損傷演化。此外，Chen等[26]通過電子顯微鏡對巖石蠕變破壞機理的研究同樣證實，只有當施加的應力超過屈服極限時，微裂紋擴展才會加速。在此基礎上，本文給出一種新的熱耦合元件(即熱黏塑性體)，來表征巖石在不同溫度下的損傷演化對其蠕變變形的影響(圖4c)。試驗結果表明，由于微裂紋擴展，巖石的蠕變速率呈不斷增加的趨勢，尤其是高溫環境下這種現象更加明顯。該熱黏塑性體中的黏壺元件為受溫度和應力影響的牛頓體，其本構關系如下：

(8)

式中：σv——作用在黏壺的應力；

η3(T,D)——與溫度T和損傷變量D有關的黏滯系數；

εvp——黏塑性應變。

為了考慮溫度T和損傷演化對蠕變變形的影響，提出黏度系數η3的表達式：

η3(T,D)=η3(T)(1-D)

(9)

熱黏塑性損傷耦合元件的總應力σ為作用在牛頓黏壺上的應力σv與塑性元件上的應力σp之和。因此，塑性元件上的應力σp可表示為：

(10)

式中：σs——臨界損傷應力。

σs可用式(6)進行描述。聯立公式(7)～(10)可得：

(11)

令折減函數p(t)=exp(-αt)，α取不同值時，p(t)隨時間t的變化規律如圖5所示。可以看出，折減函數隨時間逐漸減小，黏滯系數η3(T,D)因巖石損傷蠕變而逐漸衰減。固定應力水平下，初始條件為時間t= 0時的黏塑性應變εvp= 0。因而，可獲得熱黏塑性耦合元件的本構關系如下：

(12)

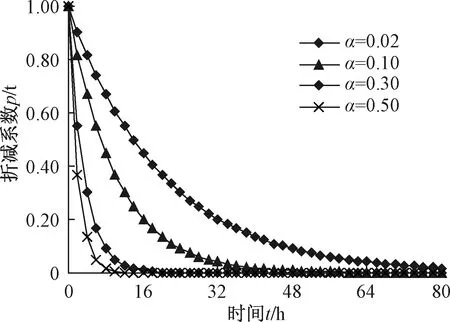
圖5 α不同時，p(t)隨時間的變化曲線

大量的蠕變試驗[27-29]結果表明巖石蠕變變形的穩定階段具有明顯的非線性特征(即不同應力水平下穩定蠕變階段的應變率與應力的比值不是常數)。宋飛等[27]通過大量的巖石蠕變試驗，分析了穩定階段蠕變速率與應力的關系，提出了非線性的黏滯分量，其中黏滯系數與應力呈指數變化關系。基于此，本文提出一種新的反映臨界應力并與溫度有關的非線性黏滯分量，本構關系如下：

(13)

式中：η1(T)——熱黏彈性體的黏滯系數；

λ——與溫度有關的黏性參數；

εv——黏塑性應變。

固定應力水平下的蠕變方程為：

(14)

2.2 熱-黏-彈-塑性損傷蠕變本構模型

圖6給出了本文模型蠕變變形隨時間曲線的示意圖。可以看出，相比傳統的西原模型，當σ<σs時，穩態階段的蠕變速率不為0，非線性Newton體的黏滯系數與溫度和施加應力的大小有關，而在Burgers模型中Newton體的黏滯系數為常數；當σ≥σs時，考慮了巖石脆性斷裂損傷引發的加速蠕變，明顯不同于傳統的西原模型和Burgers模型。

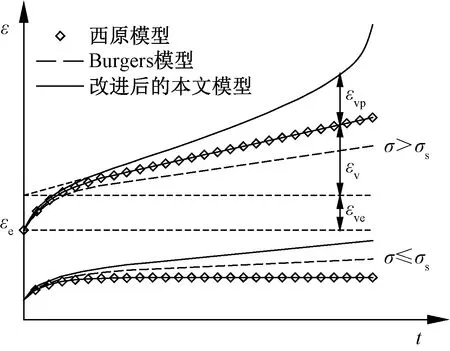
圖6 改進后本文模型的應力-應變關系

圖4c中模型的瞬時熱彈性模量為E1(T)，熱黏彈性模量為E2(T)，熱黏滯系數為η1(T)，熱黏彈性體的黏滯系數為η2(T)，熱黏塑性體的黏滯系數為η3(T,D)，元件中的臨界應力為σs。圖4c中四部分所受到的應力分別為σe，σv，σve和σvp，對應的應變分別為εe，εv，εve和εvp。本文模型滿足以下應力-應變關系：

(15)

整理公式(15)，得到一維的本構關系為：

當σ<σs時，

(16)

當σ>σs時，

(17)

當應力為常數時，可以根據疊加原理求得一維情況下的熱黏彈塑性損傷蠕變本構方程：

當σ<σs時，

(18)

當σ>σs時，

(19)

式中各符號的意義均與前述相同。

2.3 熱-黏-彈-塑性損傷蠕變本構方程的三維表達式

雖然可視化的物理元件能夠方便描述單軸應力狀態下的一維蠕變模型，但對于圍壓、軸壓同時存在的三軸應力狀態，一維蠕變模型并不適用。為此，通過引入彈、塑性理論，將應力分解為球應力張量和偏應力張量。球應力張量只產生彈性體積應變，而流變部分由偏應力張量產生[21]。

(20)

(1)熱彈性體

應力張量σij可分解為球應力張量δijσm和偏應力張量sij，即：

σij=sij+δijσm

(21)

式中δij為Kronecker符號；球應力張量δijσm只改變物體體積不改變物體形狀；偏應力張量sij改變物體形狀對體積不產生影響；平均正應力σm為：

(22)

應變張量也可分解偏應變張量eij和球應變張量δijεm：

(23)

根據廣義Hooker定律，熱彈性體的三維本構關系可描述為：

(24)

式中：G，K——剪切模量和體積模量。

根據彈性力學知識，剪切模量G、體積模量K、彈性模量E之間的關系為：

(25)

(26)

(2)熱黏性體

對于熱黏性體，考慮塑性流動法則，三維應力條件下的熱黏彈性應變為：

(27)

式中：F——屈服函數；

F0——初始狀態屈服函數值；

Q——塑性勢函數。

采用相關流動性法則，F=Q。根據Tresca屈服準則，函數F的表達式為：

(28)

(3)熱黏彈性體

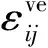
(29)

(4)熱黏塑性體

考慮塑性流動法則，三維應力狀態下熱黏塑性應變為：

(30)

式中：F——屈服函數；

F0——初始狀態屈服函數值；

Q——塑性勢函數；

< >——開關函數。

(31)

根據相關流動性法則，F≥0時，F=Q，對式(30)進行積分，可得：

(32)

聯立式(20)、(26)、(27)、(29)和(31)，可得三維應力條件下巖石熱黏彈塑性損傷蠕變方程：

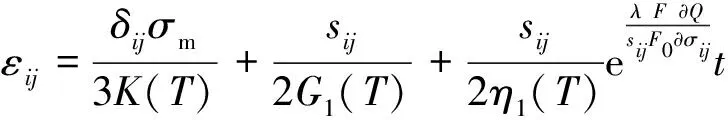
(33)

令式(33)中i=j=1，三向應力分別為σ1，σ2，σ3，傳統三軸壓縮試驗中σ2=σ3，有：

(34)

令初始狀態屈服函數值F0=1，則有：

(35)

將式(34)、(35)代入式(33)中，整理得到三軸應力狀態下的熱-力耦合損傷蠕變本構方程：

當σ1-σ3<σs時，

(36)

當σ1-σ3≥σs時，

(37)

3 模型參數的確定

巖石蠕變模型參數確定的方法已有很多，通常采用兩種類型：圖形擬合法[30]和優化分析法[17,31]。前者是根據蠕變曲線幾何形態與蠕變參數物理意義之間的對應關系，通過數據擬合來確定相應的模型參數；后者通常采用回歸分析和最小二乘法來確定模型參數。與第一類方法相比，優化分析法能夠得到更高的擬合精度，并且由于簡單適用性被廣泛應用于蠕變試驗參數的確定。為此，本文研究中將采用Levenberg-Marquardt非線性最小二乘法，對式(19)和式(37)中的熱黏彈塑性損傷蠕變模型的參數進行確定。

為了簡化模型參數確定的復雜性，分別對一維應力條件下的蠕變模型公式(19)和三維應力條件下的蠕變模型公式(37)進行簡化，形式如下：

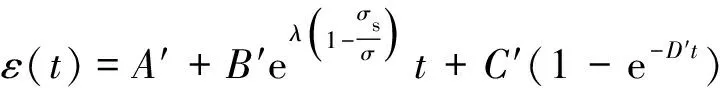
+〈E′〉[eα(T)t-1]

(38)

式中：A′，B′，C′，D′，E′——擬合參數。

一維應力條件：

(39)

三維應力條件：

(40)

4 模型驗證及參數分析

4.1 模型驗證

為了驗證本文蠕變模型的合理性，以下將采用2組試驗數據(圖3中σ3=30 MPa、T=70℃的三軸蠕變試驗結果，以及文獻[7]中不同溫度下的單軸蠕變試驗結果)與本文模型的計算結果對比分析，分別如圖7和圖8所示。模型的有效性取決于對試驗數據的擬合程度，本文將采用非線性最小二乘法對模型參數進行確定，通過反演得到的熱黏彈塑性損傷蠕變模型的力學參數分別見表1和表2。

圖7 本文模型與花崗巖三軸蠕變試驗值[17]的對比

由圖7和圖8可以看出，無論是單軸蠕變試驗還是三軸蠕變試驗，本文提出的熱黏彈塑性損傷蠕變模型均可準確地反映巖石在不同溫度、不同應力狀態下的蠕變變形的全過程，尤其是對加速蠕變階段的模擬效果，與試驗結果相吻合較好。說明本文建立的熱黏彈塑性損傷蠕變模型及通過反演得到的損傷蠕變力學參數是合理可靠的。

表1 圍壓為30 mPa、溫度為70℃時的損傷蠕變參數

表2 不同溫度下的損傷蠕變參數(σ3=0 mPa)

圖8 本文模型與花崗巖單軸蠕變試驗值[7]的對比

根據表2中不同溫度下對試驗數據進行反演得到的蠕變模型力學參數，從而得到模型參數與溫度之間的函數關系：

(41)

由上式可知，彈性模量E2、黏滯系數η1、η2和η3隨溫度的增加逐漸減小；λ為常數；損傷參數α隨溫度的增加而增大，表明在溫度越高同等外部應力作用下巖石的損傷程度越明顯。

4.2 模型參數討論

在實例驗證的基礎上，進一步對本文蠕變模型中的主要參數進行分析討論，包括黏滯系數η1，η2，η3和損傷變量系數α。為了更好理解這些參數對巖石蠕變特性的影響，取表2中T=23℃時相應的參數，在分析某一參數的影響時，其他參數均保持不變。由式(6)可知，巖石發生損傷破壞時的臨界應力σs與巖石的固有剪切強度τ0、內摩擦角φ和斷裂韌度KIC有關，而且這3個參數有內在關聯，因而為了便于分析模型參數敏感性，取臨界應力σs為定值(即取σs=104 MPa)。

在其他參數保持不變的情況下，圖9給出了不同黏滯系數η1，η2和η3分別對應的應變隨時間變化關系曲線。由圖9可知，隨著黏滯系數η1的增加，蠕變變形穩定階段的蠕變速率逐漸增大，而對初始段和加速破壞段蠕變速率的影響相對較小，η1< 500GPa·h時巖石蠕變變形的差異性很小。初始段的瞬態蠕變速率隨著黏滯系數η2的增加而減小，且過渡到穩態階段的時間逐漸增長，而η2的變化并不會對加速變形階段的蠕變速率及最終的變形量產生影響。黏滯系數η3主要是影響加速變形階段的蠕變速率和變形量，而不會對初始瞬態階段和穩定階段的變形情況產生作用。

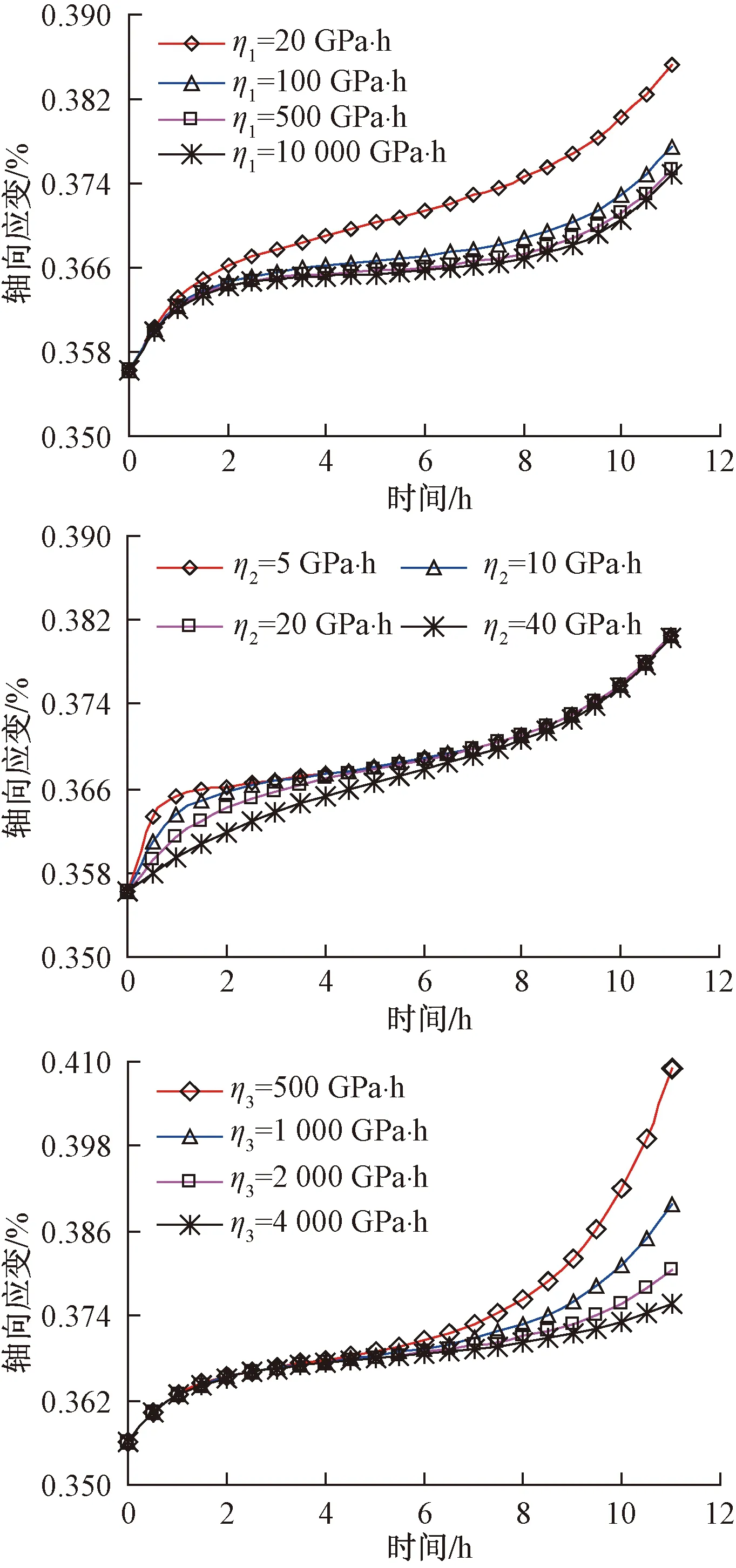
圖9 模型參數η1, η2, η3對蠕變特性的影響

不同α值下巖石的蠕變隨時間關系曲線如圖10所示。可知，參數α越大，巖石的損傷演化過程越明顯，加速蠕變階段的啟動越早；當α較小時(如α<0.41h-1)，加速蠕變階段并不顯著。說明在蠕變模型中引入損傷變量可以很好地反映巖石蠕變變形的全過程。

圖10 模型參數α對蠕變特性的影響

保持表2中T=23℃時的模型參數不變，不同臨界損傷應力σs對應的蠕變變形曲線如圖11所示，可以看出，當σ>σs時，恒定外力作用下巖石才具有明顯的加速蠕變階段，且σs越大加速蠕變過程越顯著，加速蠕變階段的啟動越早；當σ<σs時，恒定外力作用下巖石不存在加速蠕變過程，只包括初始瞬態階段和穩定變化階段，且相同時間下巖石蠕變變形隨σs增加而增大，很好地反映了巖石物理力學指標(如固有剪切強度τ0、內摩擦角φ和斷裂韌度KIC)對其蠕變特性的影響，說明本文蠕變模型在穩態蠕變階段考慮臨界損傷應力和外部荷載的非線性影響是合理的。

由上述試驗結果比對和模型參數分析可知，本文所建立的熱-力耦合作用巖石損傷蠕變模型能夠有效合理地反映巖石蠕變3個階段各自的力學形態特征以及巖石蠕變變形的全過程特征。本文損傷蠕變模型只考慮了溫度和外部應力作用的情況，并未涉及巖石內部存有裂隙以及裂隙內部存在高孔隙水壓的情況。因而，本文蠕變模型適用于分析處于高溫、高應力環境下較完整巖石的長期蠕變變形。

5 結論

(1)基于斷裂力學推導了巖石臨界損傷應力σs的表達式，提出了反映巖石穩態蠕變階段與σs相關的非線性黏性分量，并將該黏性分量、σs和指數形式的損傷變量引入到巖石的流變本構關系和蠕變方程中，建立了新的熱-力耦合的巖石損傷蠕變模型；當外部應力σ>σs時，巖石蠕變變形全過程具有明顯三階段特征：初始瞬態階段、穩態階段和加速蠕變階段；當σ<σs時，巖石蠕變只包含前兩個階段。

(2)利用非線性最小二乘法得到了蠕變模型的擬合表達式，并通過反演獲得了巖石損傷蠕變模型的力學參數，通過計算驗證了本文蠕變模型和反演所得蠕變力學參數的可靠性。

(3)比對不同溫度、不同應力條件下花崗巖三軸蠕變試驗數據的結果表明，相比傳統西原模型和Burgers模型，本文蠕變模型的計算結果能夠更好地反映巖石在初始瞬態、穩態和加速蠕變階段全過程的變形規律。

(4)模型參數的分析情況如下：黏滯系數η3、損傷變量系數α、和臨界損傷應力σs的大小顯著影響巖石的蠕變特性；η3和α越小、σs越大，巖石的損傷演化過程越明顯，加速蠕變階段啟動越早；黏滯系數η2越小由初始瞬態過渡到穩態階段的時間越早，但不會影響巖石后期的蠕變速率和最終的蠕變值；黏滯系數η1越大，對應的蠕變速率和蠕變變形越小，當η1增大到一定值時，其影響可以忽略。

本文建立的巖石損傷蠕變模型適用于分析高溫、高應力環境下較完整巖石的長期蠕變變形，并未涉及巖石內部存有裂隙以及裂隙內部含有高孔隙水壓的情況。